归并排序和快速排序都用到了分治思想，时间复杂度为 O(nlogn) 的排序算法。更常用，更法适合大规模的数据排序。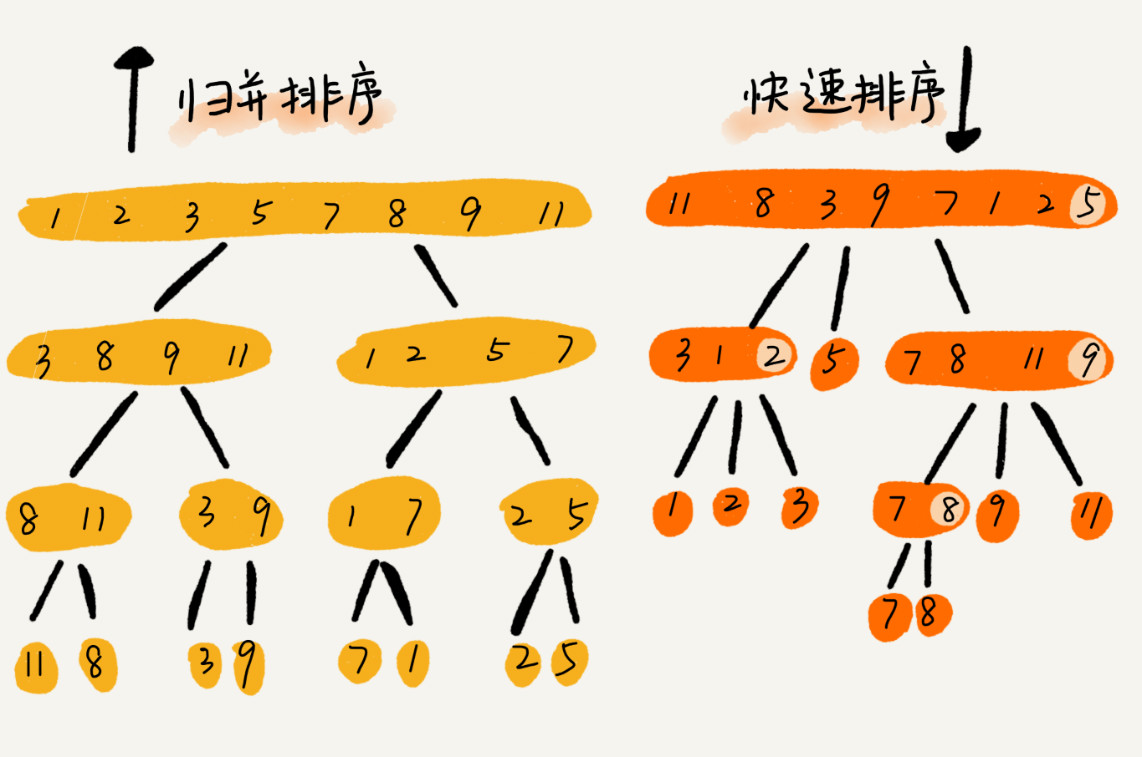
image.png

归并排序(Merge Sort)

原理

将数组分成 2 个较小的数组，然后每个数组再分成两个更小的数组，直至每个数组里只包含一个元素，然后将小数组不断的合并成较大的数组，直至只剩下一个数组，就是排序完成后的数组序列。
归并、快排 - 图3
分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧

代码实现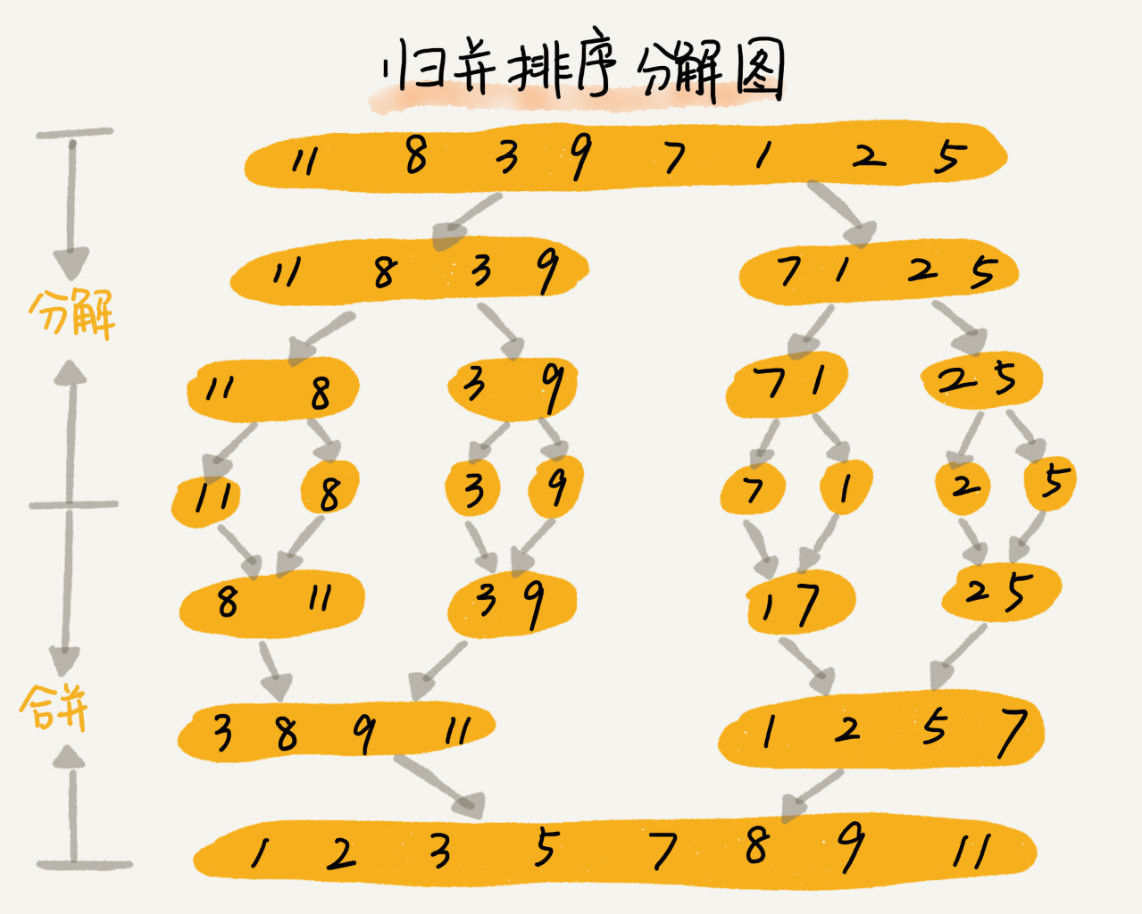image.png

  1. // 分的方法
  2. function mergeSort(arr) {
  3.   if (arr.length == 1) {
  4.     return arr
  5.   } else {
  6.     let mid = parseInt(arr.length / 2)
  7.     let left = arr.slice(0, mid)
  8.     let right = arr.slice(mid)
  9.     console.log("mergeSort：", left, right)
  10.     return merge(mergeSort(left), mergeSort(right)) // 先递归左半部分数组，深度优先
  11.   }
  12. }
  14. // 合并的方法
  15. function merge(left, right) {
  16.   // 深度优先，进来执行的时候，先是长度为1的数组了
  17.   console.log("merge：", left, right)
  18.   let temp = new Array()
  19.   while (left.length > 0 && right.length > 0) {
  20.     if (left[0] < right[0]) {
  21.       temp.push(left.shift())
  22.     } else {
  23.       temp.push(right.shift())
  24.     }
  25.   }
  26.   return temp.concat(left, right)
  27. }
  28. mergeSort([4, 1, 5, 8, 7, 3])
  29. // mergeSort： [ 4, 1, 5 ] [ 8, 7, 3 ]
  30. // mergeSort： [ 4 ] [ 1, 5 ]
  31. // mergeSort： [ 1 ] [ 5 ]
  32. // merge： [ 1 ] [ 5 ]
  33. // merge： [ 4 ] [ 1, 5 ]
  34. // mergeSort： [ 8 ] [ 7, 3 ]
  35. // mergeSort： [ 7 ] [ 3 ]
  36. // merge： [ 7 ] [ 3 ]
  37. // merge： [ 8 ] [ 3, 7 ]
  38. // merge： [ 1, 4, 5 ] [ 3, 7, 8 ]

复杂度

归并排序稳不稳定关键要看 merge() 函数，在合并的过程中，如果 A[p…q] 和 A[q+1…r] 之间有值相同的元素，那可以先把 A[p…q] 中的元素放入 tmp 数组。这样就保证了值相同的元素，在合并前后的先后顺序不变。所以归并排序是一个稳定的排序算法。
时间复杂度：归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
空间复杂度：归并排序不是原地排序算法。因为合并函数在合并两个数组的时候，需要借助额外的存储空间。但是尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。所以在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

快速排序(Quicksort)

归并排序的时间复杂度任何情况下都是 O(nlogn)，看起来非常优秀。但是，归并排序并没有像快排那样，应用广泛，这是为什么呢？因为它有一个致命的“弱点”，那就是归并排序不是原地排序算法。

原理

和归并排序一致，它也使用了分治策略的思想，它也将数组分成一个个小数组，但与归并不同的是，它实际上并没有将它们分隔开。
快排的过程简单的说只有三步：

  • 首先从序列中随机选取一个数作为基准数
  • 将比这个数大的数全部放到它的右边，把小于或者等于它的数全部放到它的左边 （一次快排 partition）
  • 然后分别对基准的左右两边重复以上的操作，直到数组完全排序

归并、快排 - 图5

代码实现

  1. 创建两个指针分别指向数组的最左端以及最右端
  2. 在数组中任意取出一个元素作为基准：
    1. 最简单的一种做法是每次都是选择最左边的元素作为基准；但这对几乎已经有序的序列来说，并不是最好的选择，它将会导致算法的最坏表现。
    2. 还有一种做法，就是选择中间的数或通过 Math.random() 来随机选取一个数作为基准
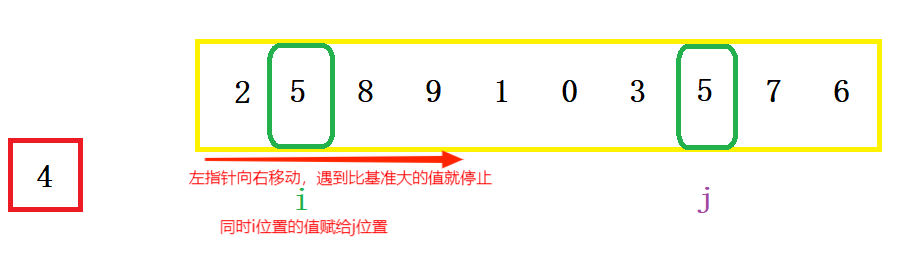
  3. 右指针开始向左移动，遇到比基准小的元素停止，交换左右指针所指向的元素
  4. 左指针开始向右移动，遇到比基准大的停止
  5. 重复 3，4，直到左指针超过右指针，此时，比基准小的值就都会放在基准的左边，比基准大的值会出现在基准的右边
  6. 然后分别对基准的左右两边重复以上的操作，直到数组完全排序

20210419094146585.png
20210419094351749.png20210419094520275.png
image.png

function sort(arr, begin, end) {
  if (begin < end) {
    let i = begin
    let j = end
    let base = arr[begin] // 选取最左边的作为基准
    while (i < j) { 
      // 先移动右指针
      while (arr[j] > base && i < j) { // 当一旦找到一个比基准小的就停止
        j--
      }
      arr[i] = arr[j] // j位置的值赋给i位置
      // 再移动左指针
      while (arr[i] < base && i < j) { // 当一旦找到一个比基准大的就停止
        i++
      }
      arr[j] = arr[i] // 交换位置
      // 然后再开启新的一轮循环，继续移动右指针···
    }
    arr[i] = base // 循环结束后，再将基准值赋给i位置
    sort(arr, begin, i - 1) // 然后再递归处理基准值左右两边，一直到有序
    sort(arr, i + 1, end)
  } else {
    return
  }
}

let arr = [2, 3, 1, 4, 8, 7, 9, 6]
sort(arr, 0, 7)
console.log(arr)

复杂度

快速排序通过将j位置赋给i位置，可以实现原地排序，解决了归并排序占用太多内存的问题。但是交换位置会改变现后顺序，所以快排是一种原地、不稳定的排序算法。
时间复杂度：大部分情况是 O(nlogn)，只有在极端情况才会退化到O(n2)。极端情况就是如已经有序的递增数列，一直选取最后一个作为基准值。

最优最通用的排序

首先通用的排序算法肯定不能是线性的，所以排除了桶排序、计数排序、基数排序，而最优肯定不能用时间复杂度为O(n2)的冒泡、选择、插入算法。所以就只能归并和快排。
快排在最坏情况下的时间复杂度是 O(n2)，而归并排序可以做到平均情况、最坏情况下的时间复杂度都是 O(nlogn)，看起来很诱人，但是空间复杂度是 O(n)，所以归并用的并不多。
所以最优最通用的排序就是优化一下快排，解决快排在极端情况下时间复杂度为O(n2)的问题。 而快排O(n2) 时间复杂度出现的主要原因还是因为分区点选的不够合理。最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多。介绍两个常用简单的分区算法：

三数取中法

从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。但是，如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”。

随机法

随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能会出现每次分区点都选的很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况，出现的可能性不大。