平衡二叉查找树

目的

解决普通二叉查找树在频繁的插入、删除等动态更新的情况下，出现时间复杂度退化的问题。“平衡”就是让整棵树左右看起来比较“对称”，不要出现左高右矮的情况，让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

定义

平衡二叉树中任意一个节点的左右子树的高度相差不能大于 1。
完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。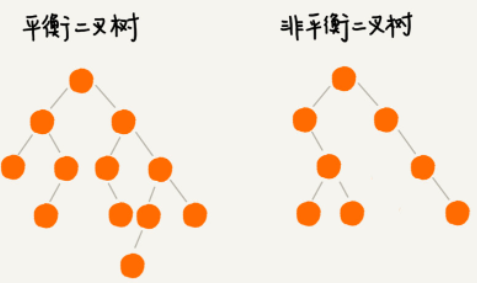
image.png
平衡二叉树：Splay Tree（伸展树）、Treap（树堆）、AVL树

红黑树(R-B Tree)

红黑树并不是严格意义上的平衡二叉树，因为它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。但是只要树的高度不比 log2n 大很多，红黑树的高度近似 2log2n。，尽管它不符合严格的平衡二叉查找树的定义，但仍然是一个合格的平衡二叉查找树。
AVL是严格的平衡二叉查找树，查找效率非常高，但为了维持这种高度的平衡，就要付出更多的代价：每次插入、删除都要做调整，比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用 AVL 树的代价就有点高了。
红黑树只是做到了近似平衡，并不是严格的平衡，红黑树的插入、删除、查找各种操作性能都比较稳定，所以在维护平衡的成本上，要比 AVL 树要低。

定义

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，还需要满足：

  • 根节点是黑色的；插入节点是红色
  • 任何上下相邻的节点不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
  • 每个节点，从该节点到达其叶子节点的所有路径，都包含相同数目的黑色节点；
  • 叶子节点必须是黑色的空节点（NIL）

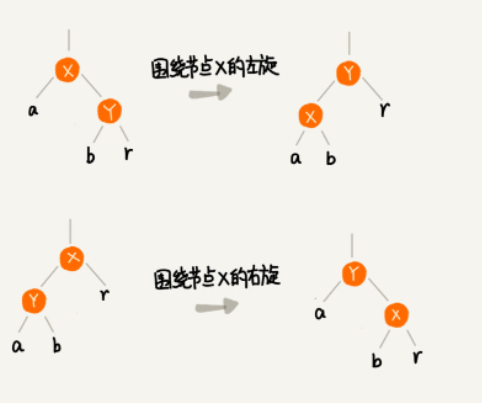
在插入、删除节点的过程中，第二、第三点要求可能会被破坏，所以左旋（rotate left）、右旋（rotate right），实际上就是要把被破坏的第二、第三点恢复过来。
image.pngimage.png
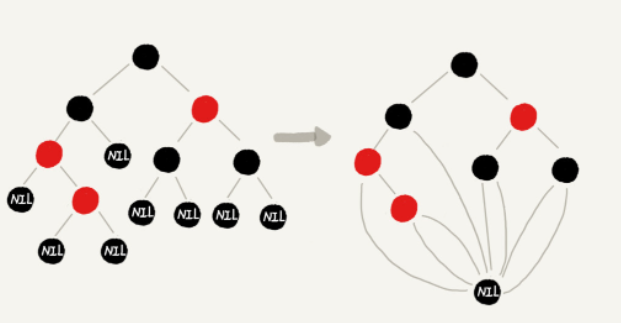
第四条“叶子节点必须是黑色的空节点”，主要是当插入新节点的时候，其父节点也是红色这种情况也能满足下面CASE 2。同时具体实现中并不会浪费存储空间，可以共用一个黑色的、空的节点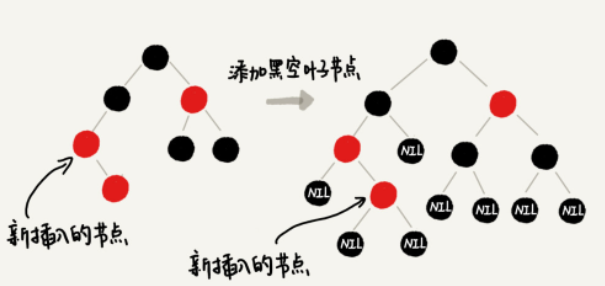
image.png
image.png

插入

红黑树规定，插入的节点必须是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。
插入普通情况：

  • 如果插入节点的父节点是黑色的，那什么都不用做。
  • 如果插入的节点是根节点，那直接改变它的颜色，把它变成黑色就可以了。

三种特殊情况：

把父节点的兄弟节点叫作叔叔节点，父节点的父节点叫作祖父节点。

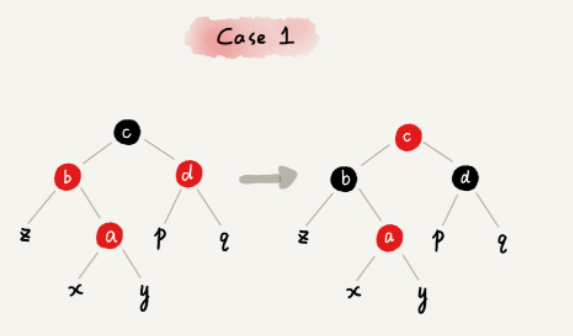
CASE 1：如果关注节点是 a，它的叔叔节点 d 是红色，就依次执行下面的操作：

  • 将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色；
  • 将关注节点 a 的祖父节点 c 的颜色设置成红色；
  • 关注节点变成 a 的祖父节点 c；
  • 跳到 CASE 2 或者 CASE 3。

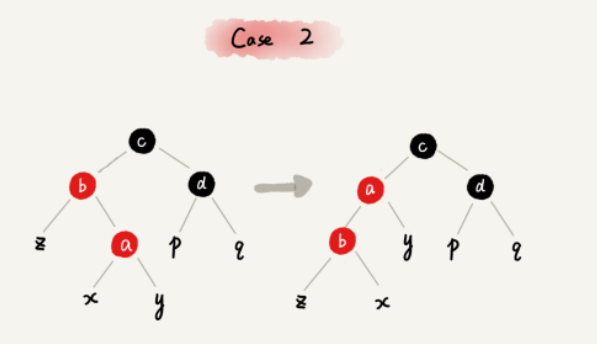
image.png
CASE 2：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点，就依次执行下面的操作：

  • 关注节点变成节点 a 的父节点 b；
  • 围绕新的关注节点b 左旋；
  • 跳到 CASE 3。

image.png
CASE 3：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点，就依次执行下面的操作：

  • 围绕关注节点 a 的祖父节点 c 右旋；
  • 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换。
  • 调整结束。

image.png

删除

一、针对删除节点初步调整
初步调整保证整棵红黑树在一个节点删除之后，仍然满足最每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点。
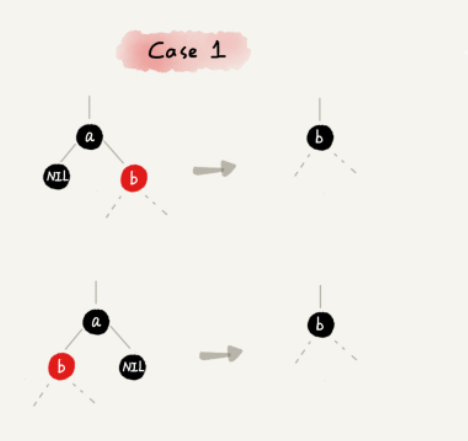
CASE 1：如果要删除的节点是 a，它只有一个子节点 b，那就依次进行下面的操作：

  • 删除节点 a，并且把节点 b 替换到节点 a 的位置，这一部分操作跟普通的二叉查找树的删除操作一样；
  • 节点 a 只能是黑色，节点 b 也只能是红色，其他情况均不符合红黑树的定义。这种情况下，把节点 b 改为黑色；
  • 调整结束，不需要进行二次调整。

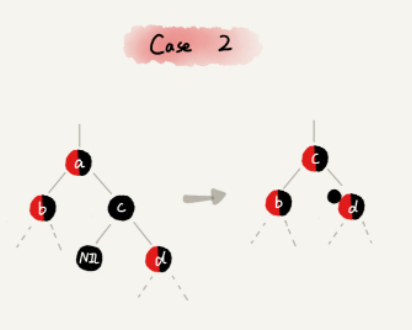
image.png
CASE 2：如果要删除的节点 a 有两个非空子节点，并且它的后继节点就是节点 a 的右子节点 c。就依次进行下面的操作：

  • 如果节点 a 的后继节点就是右子节点 c，那右子节点 c 肯定没有左子树。把节点 a 删除，并且将节点 c 替换到节点 a 的位置。这一部分操作跟普通的二叉查找树的删除操作无异；
  • 然后把节点 c 的颜色设置为跟节点 a 相同的颜色；
  • 如果节点 c 是黑色，为了不违反红黑树的最后一条定义，我们给节点 c 的右子节点 d 多加一个黑色，这个时候节点 d 就成了“红 - 黑”或者“黑 - 黑”；
  • 这个时候，关注节点变成了节点 d，第二步的调整操作就会针对关注节点来做。

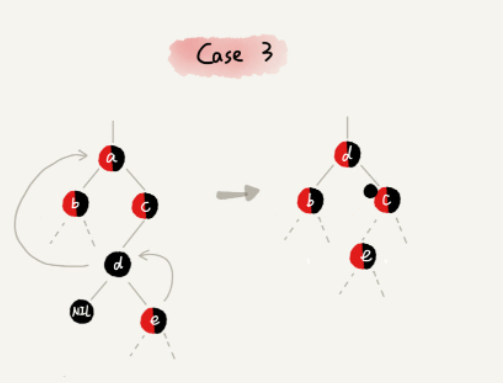
image.png
CASE 3：如果要删除的是节点 a，它有两个非空子节点，并且节点 a 的后继节点不是右子节点，就依次进行下面的操作：

  • 找到后继节点 d，并将它删除，删除后继节点 d 的过程参照 CASE 1；
  • 将节点 a 替换成后继节点 d；
  • 把节点 d 的颜色设置为跟节点 a 相同的颜色；
  • 如果节点 d 是黑色，为了不违反红黑树的最后一条定义，给节点 d 的右子节点 c 多加一个黑色，这个时候节点 c 就成了“红 - 黑”或者“黑 - 黑”；
  • 这个时候，关注节点变成了节点 c，第二步的调整操作就会针对关注节点来做。

image.png
二、针对关注节点进行二次调整
保证了不存在上下相邻的两个红色节点。
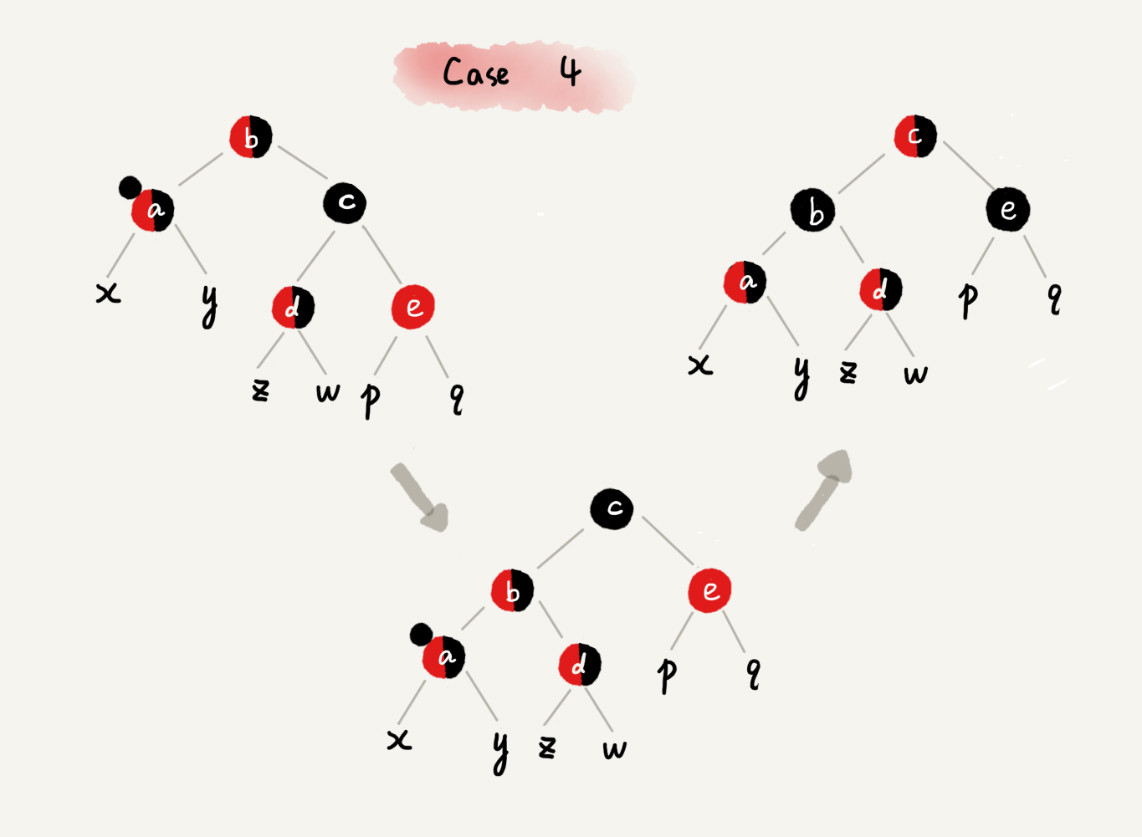
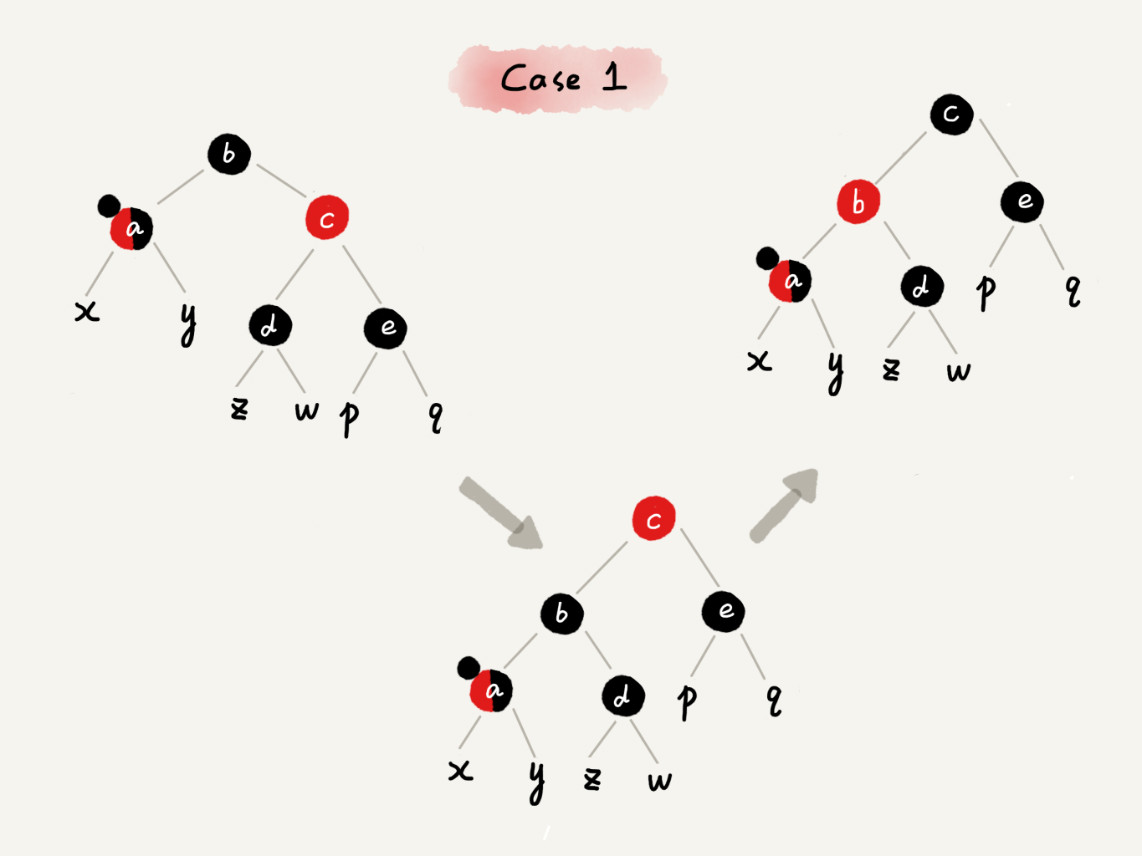
CASE 1：如果关注节点是 a，它的兄弟节点 c 是红色的，就依次进行下面的操作：

  • 围绕关注节点 a 的父节点 b 左旋；
  • 关注节点 a 的父节点 b 和祖父节点 c 交换颜色；
  • 关注节点不变；
  • 继续从四种情况中选择适合的规则来调整。

image.png
CASE 2：如果关注节点是 a，它的兄弟节点 c 是黑色的，并且节点 c 的左右子节点 d、e 都是黑色的，就依次进行下面的操作：

  • 将关注节点 a 的兄弟节点 c 的颜色变成红色；
  • 从关注节点 a 中去掉一个黑色，这个时候节点 a 就是单纯的红色或者黑色；
  • 给关注节点 a 的父节点 b 添加一个黑色，这个时候节点 b 就变成了“红 - 黑”或者“黑 - 黑”；
  • 关注节点从 a 变成其父节点 b；
  • 继续从四种情况中选择符合的规则来调整。

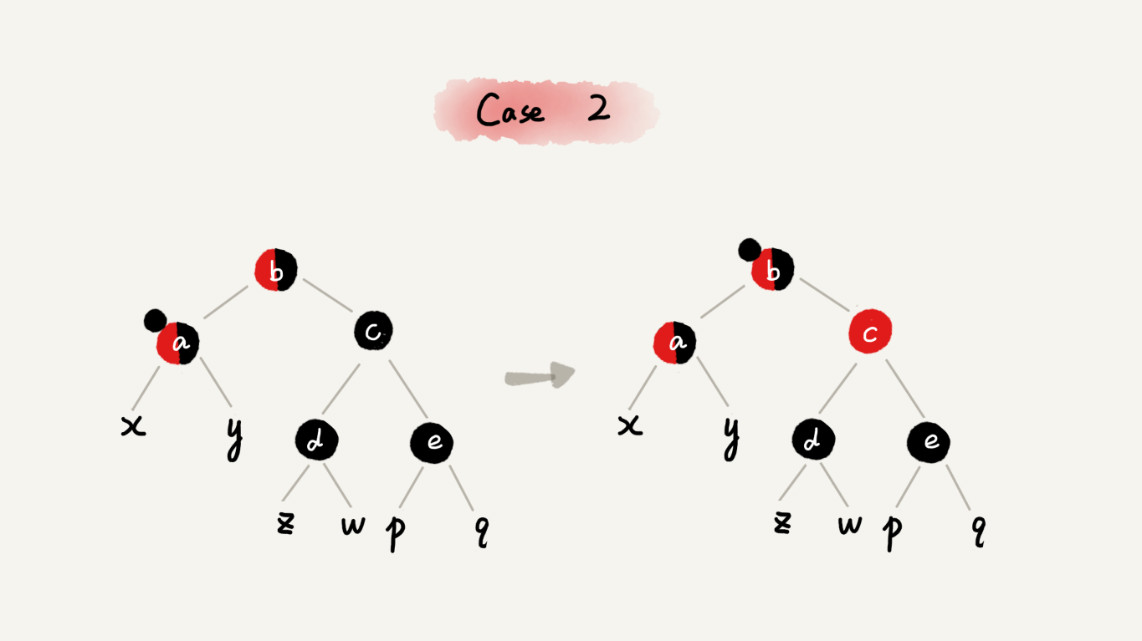
image.png
CASE 3：如果关注节点是 a，它的兄弟节点 c 是黑色，c 的左子节点 d 是红色，c 的右子节点 e 是黑色，就依次进行下面的操作：

  • 围绕关注节点 a 的兄弟节点 c 右旋；
  • 节点 c 和节点 d 交换颜色；
  • 关注节点不变；
  • 跳转到 CASE 4，继续调整。

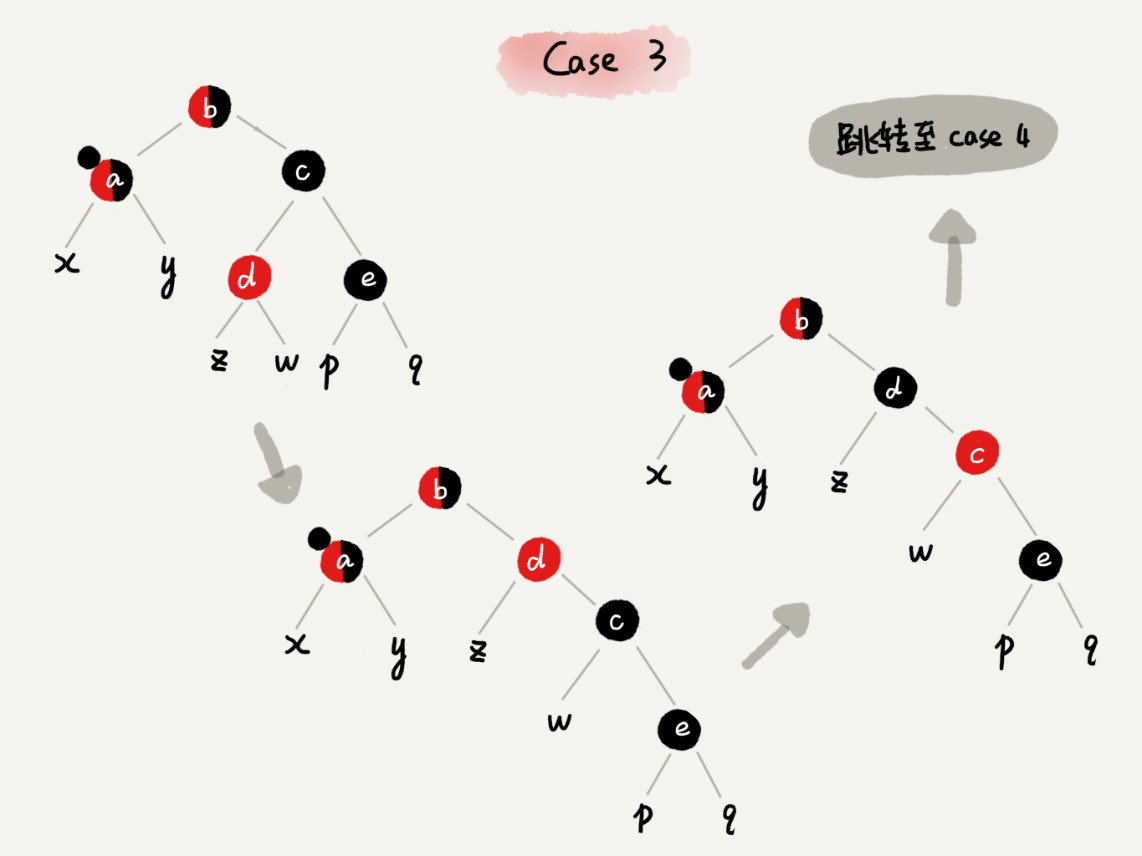
image.png
CASE 4：如果关注节点 a 的兄弟节点 c 是黑色的，并且 c 的右子节点是红色的，就依次进行下面的操作：

  • 围绕关注节点 a 的父节点 b 左旋；
  • 将关注节点 a 的兄弟节点 c 的颜色，跟关注节点 a 的父节点 b 设置成相同的颜色；
  • 将关注节点 a 的父节点 b 的颜色设置为黑色；
  • 从关注节点 a 中去掉一个黑色，节点 a 就变成了单纯的红色或者黑色；
  • 将关注节点 a 的叔叔节点 e 设置为黑色；
  • 调整结束。

image.png

代码实现

  1. /**
  2.  *
  3.  * 1. 规则
  4.  *   1. 根结点必须为黑色
  5.  *   2. 不能有R-R的关系
  6.  *   3. 每条到叶子节点的路径必须包含相同的黑色节点树
  7.  */
  9. const RedBlackTreeNode = require('./RedBlackTreeNode');
  10. const BLACK = 1;
  11. const RED = 0;
  13. class RedBlackTree {
  14.   constructor() {
  15.     this.root = null;
  16.   }
  18.   /**
  19.    * 
  20.    * @param {number} val 
  21.    * @param {RedBlackTreeNode} node 
  22.    * @return {RedBlackTreeNode}
  23.    */
  24.   _insert(val) {
  25.     let t = this.root;
  26.     let p = null;
  27.     while (t) {
  28.       p = t;
  29.       if (t.val < val) {
  30.         t = t.right;
  31.       } else if (t.val > val) {
  32.         t = t.left;
  33.       } else return;
  34.     }
  35.     let node = new RedBlackTreeNode(val);
  36.     node.parent = p;
  37.     if (p === null) {
  38.       this.root = node;
  39.     } else if (p.val < node.val) {
  40.       p.right = node;
  41.     } else {
  42.       p.left = node;
  43.     }
  44.     node.color = RED;
  45.     this.insertFix(node);
  46.   }
  48.   /**
  49.    * 
  50.    * @param {RedBlackTreeNode} node
  51.    * @param {number} val 
  52.    * @return {boolean}
  53.    */
  54.   _remove(node, val) {
  55.     while (node.val !== val && node) {
  56.       if (node.val > val) {
  57.         node = node.left
  58.       } else {
  59.         node = node.right
  60.       }
  61.     }
  62.     if (node) {
  63.       if (!node.left || !node.right) {
  64.         this._removeAndFix(node);
  65.       } else {
  66.         let minNode = this.findMin(node.right);
  67.         node.val = minNode.val;
  68.         this._remove(node.right, minNode.val);
  69.       }
  70.     } else return false;
  71.     return true
  72.   }
  74.   /**
  75.    * @param {RedBlackTreeNode} node
  76.    */
  77.   _removeAndFix(node) {
  78.     if (node.color === RED) {
  79.       this._removeNode(node);
  80.     } else {
  81.       this._removeFix(node);
  82.     }
  83.   }
  85.   /**
  86.    * 
  87.    * @param {RedBlackTreeNode} node 
  88.    */
  89.   _removeNode(node) {
  90.     if (node === this.root) {
  91.       if (node.left) {
  92.         this.root = node.left;
  93.         node.parent = null;
  94.       } else if (node.right) {
  95.         this.root = node.right;
  96.         node.parent = null;
  97.       } else {
  98.         this.root = null;
  99.       }
  100.     } else {
  101.       if (node.parent.left === node) {
  102.         if (node.left) {
  103.           node.parent.left = node.left;
  104.           node.left.parent = node.parent;
  105.         } else if (node.right) {
  106.           node.parent.left = node.right;
  107.           node.right.parent = node.parent
  108.         } else {
  109.           node.parent.left = null
  110.         }
  111.       } else {
  112.         if (node.left) {
  113.           node.parent.right = node.left;
  114.           node.left.parent = node.parent;
  115.         } else if (node.right) {
  116.           node.parent.right = node.right;
  117.           node.right.parent = node.parent
  118.         } else {
  119.           node.parent.right = null
  120.         }
  121.       }
  122.     }
  123.   }
  125.   /**
  126.    * 
  127.    * @param {RedBlackTreeNode} node 
  128.                                                                                                            */
  129.   _removeFix(node) {
  130.     let nodeRef = node;
  131.     while (node !== this.root && node.color === BLACK) {
  132.       if (node.parent.left === node) {
  133.         let brotherNode = node.parent.right;
  134.         if (brotherNode.color === RED) {
  135.           brotherNode.color = BLACK;
  136.           node.color = BLACK;
  137.           node.parent.color = RED;
  138.           this._rotateLeft(node.parent);
  139.         } else if (
  140.           (!brotherNode.left || brotherNode.left.color === BLACK)
  141.           &&
  142.           (!brotherNode.right || brotherNode.right.color === BLACK)
  143.         ) {
  144.           if (node.parent.color === RED) {
  145.             brotherNode.color = RED;
  146.             node.parent.color = BLACK;
  147.             node = this.root;
  148.           } else {
  149.             brotherNode.color = RED;
  150.             node = node.parent;
  151.           }
  152.         } else if (brotherNode.left.color === RED && brotherNode.right.color === BLACK) {
  153.           this._rotateRight(brotherNode);
  154.           brotherNode.color = RED;
  155.           brotherNode.parent.color = BLACK;
  156.         } else if (brotherNode.right.color === RED) {
  157.           brotherNode.color = node.parent.color;
  158.           node.parent.color = BLACK;
  159.           brotherNode.right.color = BLACK;
  160.           this._rotateLeft(node.parent);
  161.           node = this.root;
  162.         }
  163.       } else {
  164.         let brotherNode = node.parent.left;
  165.         if (brotherNode.color === RED) {
  166.           brotherNode.color = BLACK;
  167.           node.color = BLACK;
  168.           node.parent.color = RED;
  169.           this._rotateRight(node.parent);
  170.         } else if (
  171.           (!brotherNode.left || brotherNode.left.color === BLACK)
  172.           &&
  173.           (!brotherNode.right || brotherNode.right.color === BLACK)
  174.         ) {
  175.           if (node.parent.color === RED) {
  176.             brotherNode.color = RED;
  177.             node.parent.color = BLACK;
  178.             node = this.root;
  179.           } else {
  180.             brotherNode.color = RED;
  181.             node = node.parent;
  182.           }
  183.         } else if (brotherNode.right.color === RED && brotherNode.left.color === BLACK) {
  184.           this._rotateLeft(brotherNode);
  185.           brotherNode.color = RED;
  186.           brotherNode.parent.color = BLACK;
  187.         } else if (brotherNode.left.color === RED) {
  188.           brotherNode.color = node.parent.color;
  189.           node.parent.color = BLACK;
  190.           brotherNode.left.color = BLACK;
  191.           this._rotateRight(node.parent);
  192.           node = this.root;
  193.         }
  194.       }
  195.     }
  196.     node.color = BLACK;
  197.     this._removeNode(nodeRef);
  198.   }
  200.   /**
  201.    * 
  202.    * @param {RedBlackTreeNode} node 
  203.    */
  204.   insertFix(node) {
  205.     while (node.parent && node.parent.color !== BLACK) {
  206.       if (node.parent === node.parent.parent.left) {
  207.         let uncleNode = node.parent.parent.right;
  208.         if (uncleNode && uncleNode.color === RED) {
  209.           node.parent.color = BLACK;
  210.           uncleNode.color = BLACK;
  211.           node.parent.parent.color = RED;
  212.           node = node.parent.parent;
  213.         } else if (node === node.parent.right) {
  214.           node = node.parent;
  215.           this._rotateLeft(node);
  216.         } else {
  217.           node.parent.color = BLACK;
  218.           node.parent.parent.color = RED;
  219.           this._rotateRight(node.parent.parent);
  220.         }
  221.       } else {
  222.         let uncleNode = node.parent.parent.left;
  223.         if (uncleNode && uncleNode.color === RED) {
  224.           node.parent.color = BLACK;
  225.           uncleNode.color = BLACK;
  226.           node.parent.parent.color = RED;
  227.           node = node.parent.parent;
  228.         } else if (node === node.parent.left) {
  229.           node = node.parent;
  230.           this._rotateRight(node);
  231.         } else {
  232.           node.parent.color = BLACK;
  233.           node.parent.parent.color = RED;
  234.           this._rotateLeft(node.parent.parent);
  235.         }
  236.       }
  237.     }
  238.     this.root.color = BLACK;
  239.   }
  241.   /**
  242.    * 
  243.    * @param {RedBlackTreeNode} node 
  244.    * @return {RedBlackTreeNode}
  245.    */
  246.   _rotateLeft(node) {
  247.     let rightNode = node.right;
  248.     let rightNodeLeft = rightNode.left;
  249.     node.right = rightNodeLeft;
  250.     if (rightNodeLeft) rightNodeLeft.parent = node;
  251.     rightNode.left = node;
  252.     if (node.parent) {
  253.       if (node.parent.left === node) {
  254.         node.parent.left = rightNode;
  255.       } else {
  256.         node.parent.right = rightNode;
  257.       }
  258.       rightNode.parent = node.parent;
  259.     } else {
  260.       this.root = rightNode;
  261.       rightNode.parent = null;
  262.     }
  263.     node.parent = rightNode;
  264.   }
  266.   /**
  267.    * 
  268.    * @param {RedBlackTreeNode} node 
  269.    * @return {RedBlackTreeNode}
  270.    */
  271.   _rotateRight(node) {
  272.     let leftNode = node.left;
  273.     let leftNodeRight = leftNode.right;
  274.     node.left = leftNodeRight;
  275.     if (leftNodeRight) leftNodeRight.parent = node;
  276.     leftNode.right = node;
  277.     if (node.parent) {
  278.       if (node.parent.left === node) {
  279.         node.parent.left = leftNode;
  280.       } else {
  281.         node.parent.right = leftNode;
  282.       }
  283.       leftNode.parent = node.parent;
  284.     } else {
  285.       this.root = leftNode;
  286.       leftNode.parent = null;
  287.     }
  288.     node.parent = leftNode;
  289.   }
  291.   /**
  292.    * @param {RedBlackTreeNode} node
  293.    * @return {RedBlackTreeNode}
  294.    */
  295.   findMin(node) {
  296.     if (node.left) {
  297.       return this.findMin(node.left)
  298.     } else return node
  299.   }
  301.   /**
  302.    * 
  303.    * @param {number} val 
  304.    */
  305.   insert(val) {
  306.     this._insert(val);
  307.   }
  309.   /**
  310.    * 
  311.    * @param {number} val 
  312.    * @return {boolean}
  313.    */
  314.   remove(val) {
  315.     this._remove(this.root, val);
  316.   }
  318. }
  320. const t = new RedBlackTree();
  321. t.insert(1);
  322. t.insert(13);
  323. t.insert(5);
  324. t.insert(11);
  325. t.insert(2);
  326. t.insert(14);
  327. t.insert(15);
  328. t.insert(7);
  329. t.insert(8);
  331. t.remove(13);
  333. const t2 = new RedBlackTree();
  334. t2.insert(41);
  335. t2.insert(38);
  336. t2.insert(31);
  337. t2.insert(12);
  338. t2.insert(19);
  339. t2.insert(8);
  341. t2.remove(8);
  342. t2.remove(19);
  343. t2.remove(12);
  344. t2.remove(31);
  345. t2.remove(38);
  346. t2.remove(41);
  348. module.exports = RedBlackTree;