概念

和树比起来，图是一种更加复杂的非线性表结构。树中的元素称为节点，图中的元素就叫作顶点（vertex），图中的一个顶点可以与任意其他顶点建立连接关系。把这种建立的关系叫作边（edge）。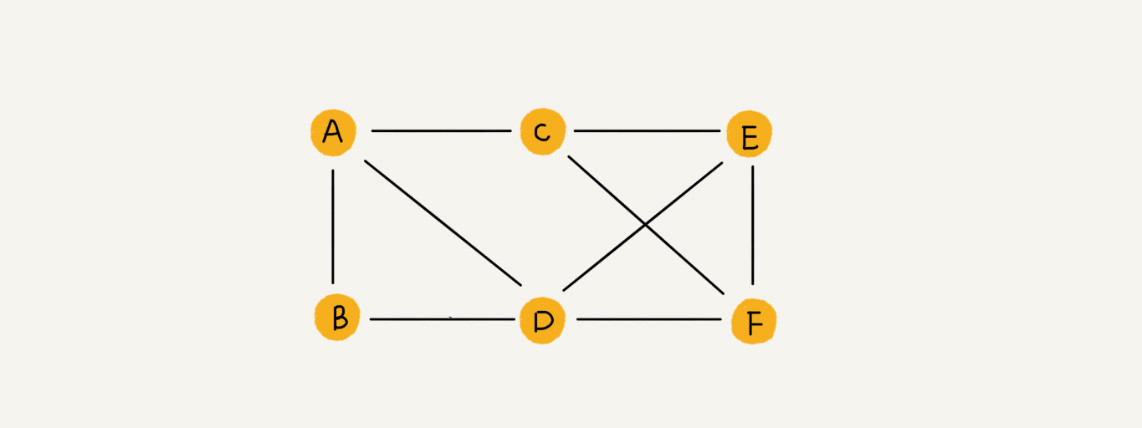
image.png
社交网络微博、微信等存储好友关系，就是一个非常典型的图结构。可以把每个用户看作一个顶点。如果两个用户之间互加好友，那就在两者之间建立一条边。所以好友关系就可以用一张图来表示。其中每个用户有多少个好友，对应到图中，就叫作顶点的度（degree），就是跟顶点相连接的边的条数。同时用户 A 关注了用户 B，但用户 B 可以不关注用户 A。这时就要稍微改造一下图结构，引入边的“方向”的概念，把这种边有方向的图叫作“有向图”。把边没有方向的图就叫作“无向图”。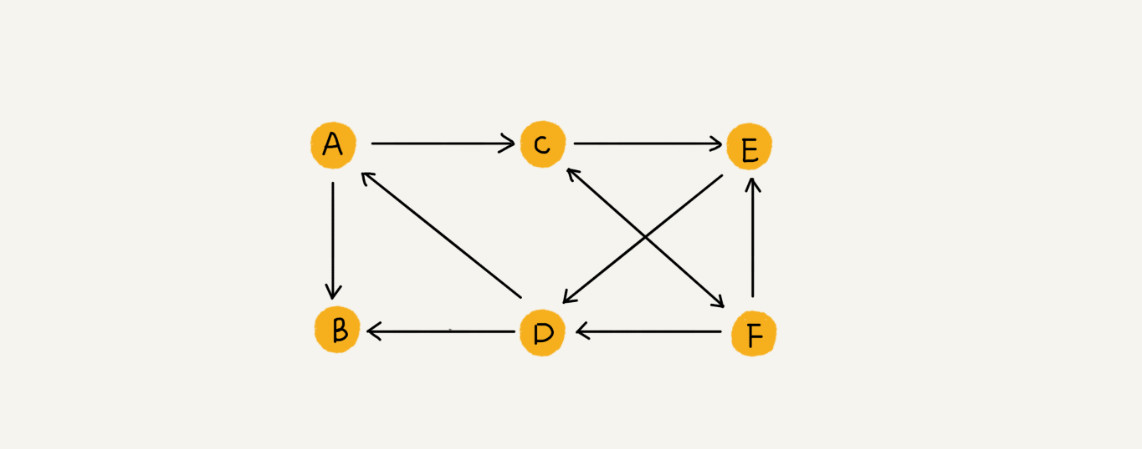
image.png
无向图中有“度”这个概念，表示一个顶点有多少条边。在有向图中，把度分为入度（In-degree）和出度（Out-degree）。顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。
带权图（weighted graph）。在带权图中，每条边都有一个权重（weight），可以通过这个权重来表示 QQ 好友间的亲密度：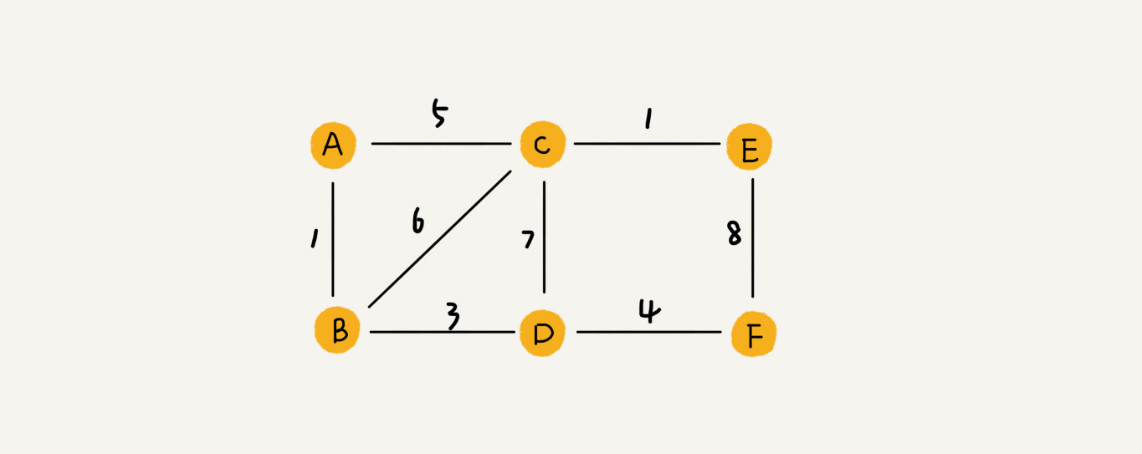
image.png

存储图的方法

邻接矩阵存储方法

邻接矩阵的底层依赖一个二维数组。对于无向图来说，如果顶点 i 与顶点 j 之间有边，就将 A[i][j] 和 A[j][i] 标记为 1；对于有向图来说，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，就将 A[i][j] 标记为 1。同理，如果有一条箭头从顶点 j 指向顶点 i 的边，就将 A[j][i]标记为 1。对于带权图，数组中就存储相应的权重。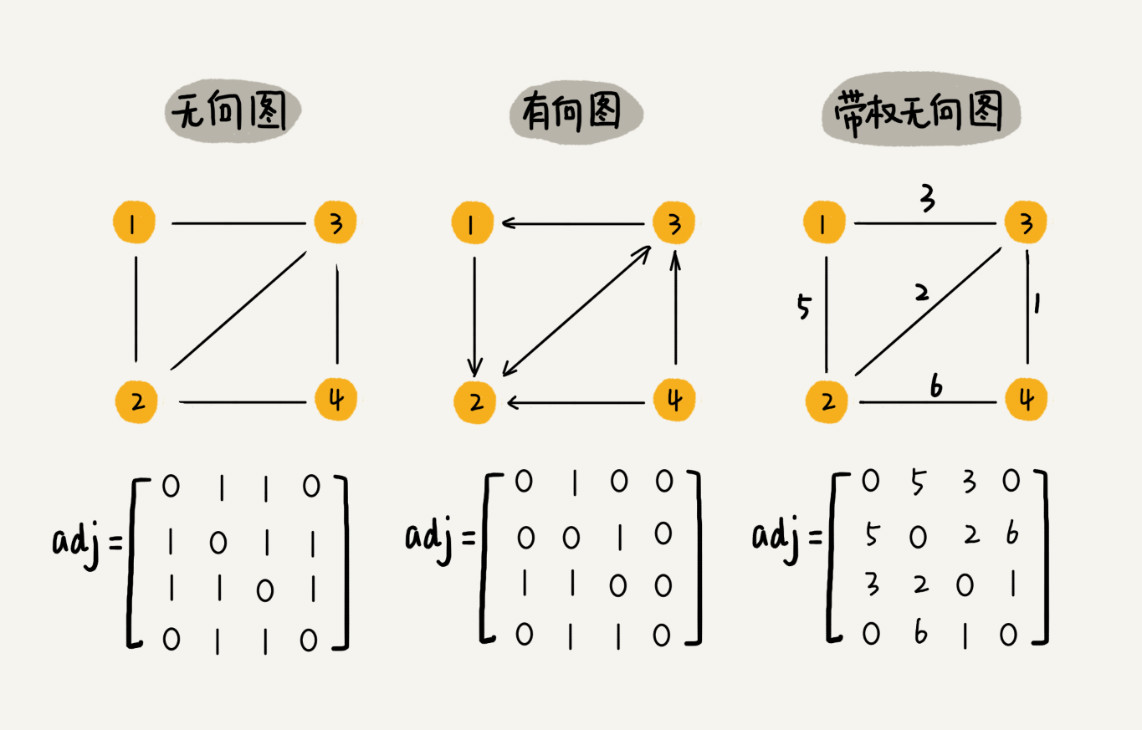
image.png
优点：用邻接矩阵来表示一个图，简单、直观。因为基于数组，所以在获取两个顶点的关系时，就非常高效。其次是方便计算，可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个Floyd-Warshall 算法，就是利用矩阵循环相乘若干次得到结果。
缺点：邻接矩阵法比较浪费存储空间。对于无向图来说，如果 A[i][j] 等于 1，那 A[j][i] 也肯定等于 1。实际上，只需要存储一个就可以，无向图的二维数组中用对角线划分为上下两部分，只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。如果存储的是稀疏图（Sparse Matrix），顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就三五百个而已。如果用邻接矩阵来存储，那绝大部分的存储空间都被浪费了。

邻接表存储方法

邻接表（Adjacency List）。主要用来解决邻接矩阵比较浪费内存空间的问题
每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。有向图的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点。对于无向图来说，每个顶点的链表中存储的，是跟这个顶点有边相连的顶点。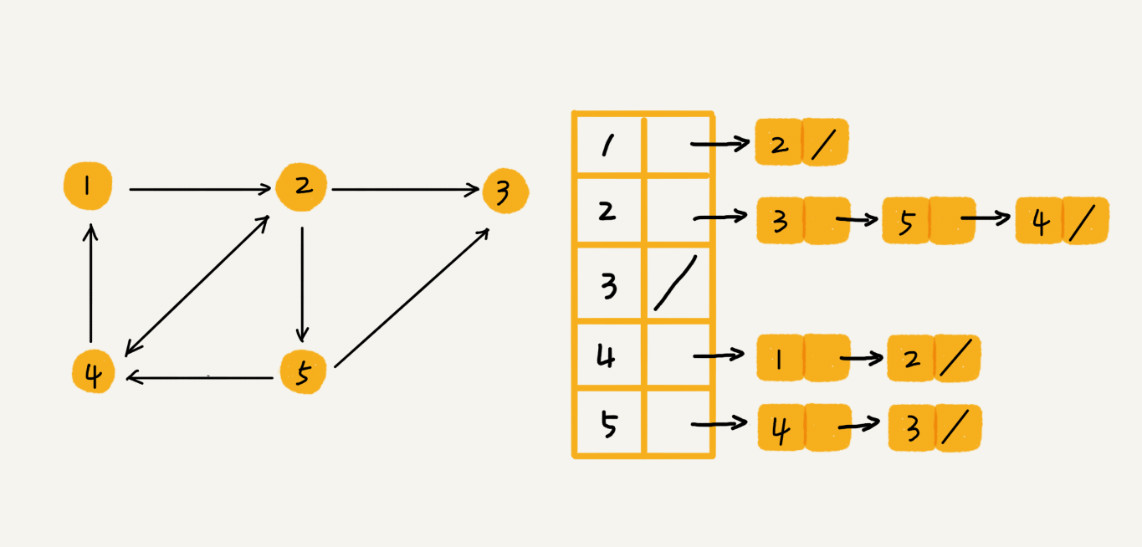
image.png
邻接矩阵存储起来比较浪费空间，但是使用起来比较节省时间。相反，邻接表存储起来比较节省空间，但是使用起来就比较耗时间。
所以为了提高查找效率，可以将链表换成其他更加高效的数据结构，比如平衡二叉查找树（比如红黑树）等。可以将邻接表中的链表改成平衡二叉查找树。还可以将链表改成有序动态数组，可以通过二分查找的方法来快速定位两个顶点之间否是存在边。

代码实现

字典和集合的主要区别就在于，集合中数据是以[值，值]的形式保存的，只关心值本身；而在字典和散列表中数据是以[键，值]的形式保存的，键不能重复，不仅关心键，也关心键所对应的值。
也可以把字典称之为映射表。由于字典和集合很相似，与Set类相似，ES6的原生Map类已经实现了字典的全部功能。

  1. class Dictionary {
  2.   constructor() {
  3.     this.items = {}
  4.   }
  6.   set(key, value) { // 向字典中添加或修改元素
  7.     this.items[key] = value
  8.   }
  10.   get(key) { // 通过键值查找字典中的值
  11.     return this.items[key]
  12.   }
  14.   delete(key) { // 通过使用键值来从字典中删除对应的元素
  15.     if (this.has(key)) {
  16.       delete this.items[key]
  17.       return true
  18.     }
  19.     return false
  20.   }
  22.   has(key) { // 判断给定的键值是否存在于字典中
  23.     return this.items.hasOwnProperty(key)
  24.   }
  26.   clear() { // 清空字典内容
  27.     this.items = {}
  28.   }
  30.   size() { // 返回字典中所有元素的数量
  31.     return Object.keys(this.items).length
  32.   }
  34.   keys() { // 返回字典中所有的键值
  35.     return Object.keys(this.items)
  36.   }
  38.   values() { // 返回字典中所有的值
  39.     return Object.values(this.items)
  40.   }
  42.   getItems() { // 返回字典中的所有元素
  43.     return this.items
  44.   }
  45. }
  46. let dictionary = new Dictionary()
  47. dictionary.set('Gandalf', 'gandalf@email.com')
  48. dictionary.set('John', 'john@email.com')
  49. dictionary.set('Tyrion', 'tyrion@email.com')
  50. console.log(dictionary.has('Gandalf')) // true
  51. console.log(dictionary.size()) // 3
  52. console.log(dictionary.keys()) // [ 'Gandalf', 'John', 'Tyrion' ]
  53. console.log(dictionary.values()) // [ 'gandalf@email.com', 'john@email.com', 'tyrion@email.com' ]
  54. console.log(dictionary.get('Tyrion')) // tyrion@email.com
  56. dictionary.delete('John')
  57. console.log(dictionary.keys()) // [ 'Gandalf', 'Tyrion' ]
  58. console.log(dictionary.values()) // [ 'gandalf@email.com', 'tyrion@email.com' ]
  59. console.log(dictionary.getItems()) // { Gandalf: 'gandalf@email.com', Tyrion: 'tyrion@email.com' }
  1. class Graph {
  2.   constructor(isDirected = false) {
  3.     this.isDirected = isDirected // 是否为有向图
  4.     this.vertices = [] // 用来存放图中的顶点
  5.     this.adjList = new Dictionary() // 用来存放图中的边(每一个顶点到相邻顶点的关系列表)
  6.   }
  8.   // 向图中添加一个新顶点
  9.   addVertex(v) {
  10.     if (!this.vertices.includes(v)) {
  11.       this.vertices.push(v)
  12.       this.adjList.set(v, [])
  13.     }
  14.   }
  16.   // 向图中添加给定的顶点a和顶点b之间的边
  17.   addEdge(a, b) {
  18.     // 如果图中没有顶点a，先添加顶点a
  19.     if (!this.adjList.has(a)) {
  20.       this.addVertex(a)
  21.     }
  22.     // 如果图中没有顶点b，先添加顶点b
  23.     if (!this.adjList.has(b)) {
  24.       this.addVertex(b)
  25.     }
  27.     this.adjList.get(a).push(b) // 在顶点a中添加指向顶点b的边
  28.     if (!this.isDirected) {
  29.        this.adjList.get(b).push(a); // 如果为无向图，则在顶点b中添加指向顶点a的边         
  30.     }
  31.   }
  33.   // 获取图的vertices
  34.   getVertices() {
  35.     return this.vertices
  36.   }
  38.   // 获取图中的adjList
  39.   getAdjList() {
  40.     return this.adjList
  41.   }
  43.   toString() {
  44.     let s = ''
  45.     this.vertices.forEach((v) => {
  46.       s += `${v} -> `
  47.       this.adjList.get(v).forEach((n) => {
  48.         s += `${n} `
  49.       })
  50.       s += '\n'
  51.     })
  52.     return s
  53.   }
  54. }
  56. // 测试
  57. let graph = new Graph()
  58. let myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
  59. myVertices.forEach((v) => {
  60.   graph.addVertex(v)
  61. })
  62. graph.addEdge('A', 'B')
  63. graph.addEdge('A', 'C')
  64. graph.addEdge('A', 'D')
  65. graph.addEdge('C', 'D')
  66. graph.addEdge('C', 'G')
  67. graph.addEdge('D', 'G')
  68. graph.addEdge('D', 'H')
  69. graph.addEdge('B', 'E')
  70. graph.addEdge('B', 'F')
  71. graph.addEdge('E', 'I')
  73. console.log(graph.toString())
  74. // A -> B C D 
  75. // B -> A E F 
  76. // C -> A D G 
  77. // D -> A C G H 
  78. // E -> B I 
  79. // F -> B 
  80. // G -> C D 
  81. // H -> D 
  82. // I -> E