冒泡排序、插入排序、选择排序三种排序算法，本质上都是对一组已知序列，进行排序，各自实现的方式不一样。但都涉及两个操作，一个是比较，一个是移动。三种时间复杂度都是 O(n**2**) 。
插入排序和冒泡排序的时间复杂度相同，都是 O(n2)，在实际的软件开发里，插入排序 > 冒泡排序，主要是因为插入排序更简洁，定义的变量更少。选择排序最次。

冒泡排序（Bubble Sort）

原理

从左到右，相邻元素进行比较，如果前一个元素值大于后一个元素值（正序），则交换，这样一轮下来，将最大的数在最右边冒泡出来。这样一轮一轮下来，最后实现从小到大排序。
冒泡、插入、选择 - 图1

代码实现

两次for循环
优化：当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。

function bubbleSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    // 优化：提前退出冒泡循环的标志位
    let isSorted = true
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        // 进来就表明不是有序的，把标记改为false
        isSorted = false
        // 利用数组解构赋值 交换j和j+1
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
    if (isSorted) {
      break
    }
  }
}

继续优化：优化每一轮比较的次数。增加一个border代表无序边界，然后把最后一次发生元素交换的位置点记下来，下一轮比较就只需要比到这儿为止。

function bubbleSort(arr) {
  // 继续优化：记录最后一次交换的边界
  let lastExchangeIndex = 0
  // 无序数组的边界，每次比较只需要比到这里为止
  let sortBorder = arr.length - 1
  for (let i = 0; i < arr.length - 1; i++) {
    let isSorted = true
    for (let j = 0; j < sortBorder; j++) { // 第二个for循环的边界就是sortBorder
      if (arr[j] > arr[j + 1]) {
        isSorted = false
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
        // 当轮循环后，此处为最后交换元素的位置
        lastExchangeIndex = j
      }
    }
    sortBorder = lastExchangeIndex // 更新第二个for循环的边界
    if (isSorted) {
      break
    }
  }
}

复杂度

冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O(1)，是一个原地排序算法。并且相邻的两个元素大小相等的时候不做交换，所以冒泡排序还是稳定的排序算法。
时间复杂度：

最好情况下，要排序的数据已经是有序的了，只需要进行一次冒泡操作，就可以结束，所以最好情况时间复杂度是 O(n)
最坏情况下，要排序的数据刚好是倒序排列的，需要进行 n 次冒泡操作，所以最坏情况时间复杂度为 O(n2)。
平均时间复杂度就是加权平均期望时间复杂度，结合概率论，满有序度 = 逆序度 + 有序度，很复杂，最后“不严格”计算结果为O(n2)

插入排序（Insertion Sort）
插入排序是将一组已知序列排序好，而不是插入新的元素进去排序！跟冒泡排序实现的功能一样，只是方式不一样！

原理

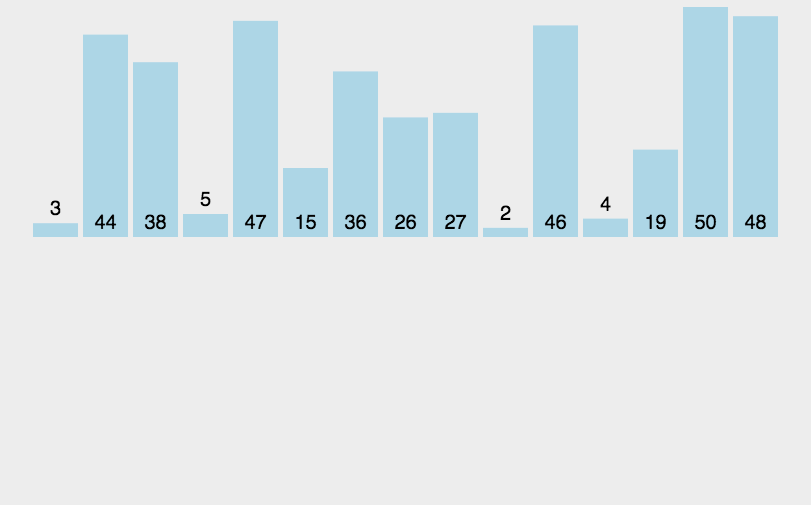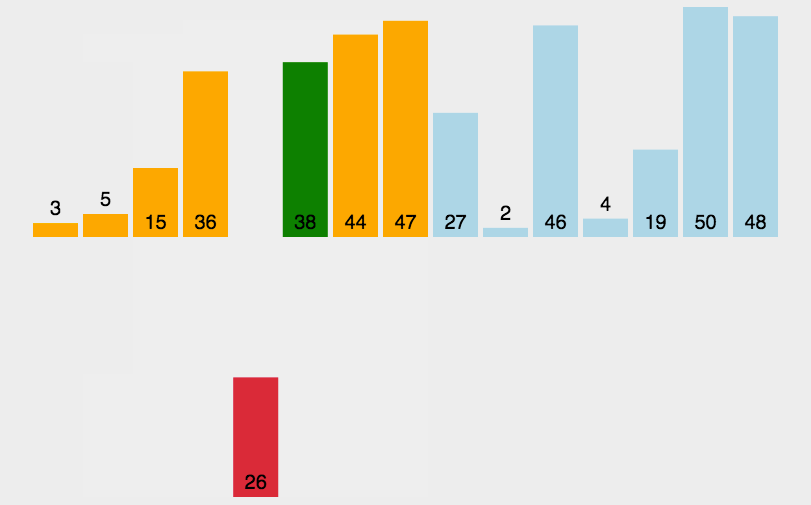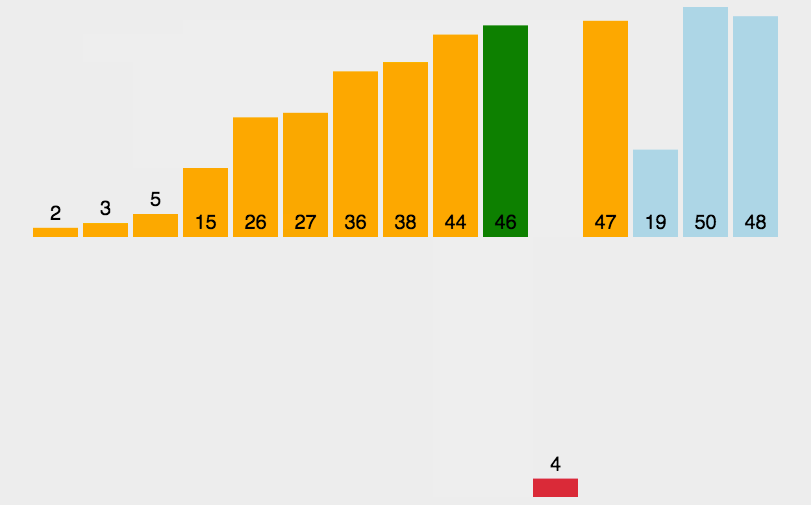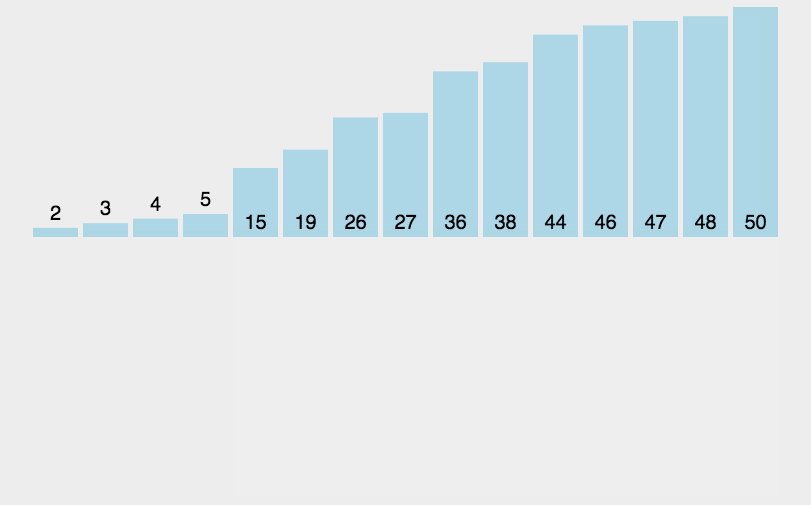
插入排序核心思想是取未排序区间中的元素，在已排序区间中从后向前扫描，找到相应位置并插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。
首先：将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素

代码实现
两个for循环
```
const insertionSort = arr => {
if (arr.length <= 1) return arr
for (let i = 0; i <= arr.length - 1; ++i) {
 // 从后往前，找当前位置的下一个，跟前面所有的数据进行相比较
 for (let j = i + 1; j > 0; --j) {
   arr[j] < arr[j - 1] && ([arr[j - 1], arr[j]] = [arr[j], arr[j - 1]])
 }
}
return arr
}
```
复杂度
插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 O(1)，是一个原地排序算法。对于值相同的元素，不进行插入不改变位置，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。
时间复杂度：
最好情况下，要排序的数据已经是有序的了，只需要从尾到头遍历已经有序的数据就可以结束，所以最好情况时间复杂度是 O(n)
最坏情况下，要排序的数据刚好是倒序排列的，需要移动大量的数据，所以最坏情况时间复杂度为 O(n2)。
在数组中插入一个数据的平均时间复杂度是 O(n)，而插入排序的操作相当于在数组中插入一个数据，同时循环执行 n 次插入操作，所以平均时间复杂度为 O(n2)。
希尔排序
希尔排序本质上是一种插入排序，但是对数列进行了等间隔分组处理，在每一组中做插入排序，直至从宏观上看起来有序，最后插入排序起来就容易了 (无须多次移位或交换)。这一优化使得原本 O(n2) 的时间复杂度一下降为 O(nlogn)。
例如：
```
let arr = [4, 1, 5, 8, 7, 3]
/**
* 排序前：将该数组看成三组（ Math.floor(arr.length/2) )，分别是： [4, 1] ， [5, 8] ， [7, 3]
* ● 第一趟排序：对三组数据分别进行插入排序，因此三个数组得到的结果为： [1, 4] ， [5, 8] ， [3, 7]
* 此时数组是这样子的：[1, 4, 5, 8, 3, 7] (从宏观上是有序的了)
* ● 第二趟排序：增量减少了，上面增量是3 ，此时增量为 1，因此把 [1, 4, 5, 8, 3, 7] 看成一个数组，对其进行插入排序，直至有序
*/
```
代码实现：
三个for循环 ```javascript function shellSort(arr) { // 每轮组数(增量) /2 for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) { // 内层循环与插入排序的写法基本一致，只是每次移动的步长变为 gap for (let i = gap; i < arr.length; i++) { let j = i let temp = arr[j] for (; j > 0; j -= gap) {
```
 if (temp >= arr[j - gap]) {
   break
 }
 arr[j] = arr[j - gap]
```
} arr[j] = temp } } return arr }

// 测试 let arr = [2, 5, 10, 7, 10, 32, 90, 9, 11, 1, 0, 10] console.log(shellSort(arr))

**复杂度分析**

- 时间复杂度：O(nlogn)
- 空间复杂度：O(1)
<a name="VnIXT"></a>
# 选择排序（Selection Sort）
<a name="zbx2o"></a>
## 原理
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。<br />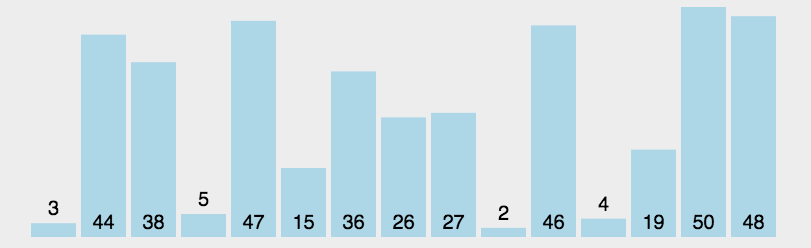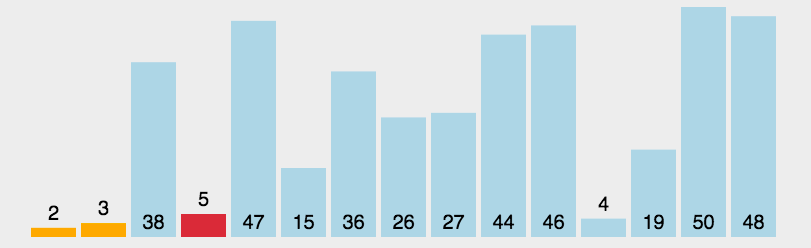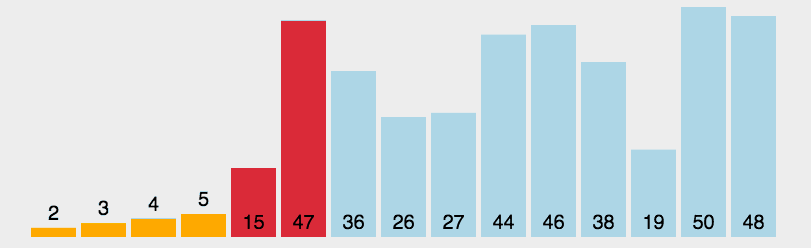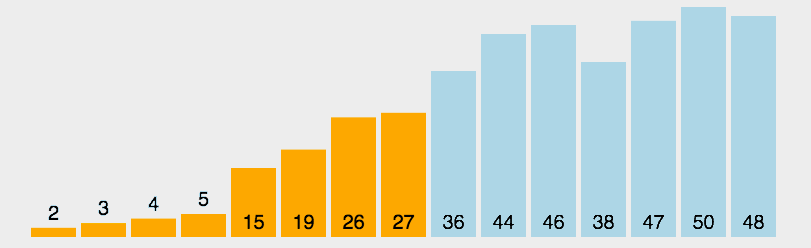![ab895950-e024-4a29-a5e1-b69f24968f3e.gif](https://cdn.nlark.com/yuque/0/2022/gif/915768/1653272770095-a80d8909-806f-4ed9-b53b-326eb3c1eae3.gif#clientId=u0792e8bc-9ceb-4&crop=0&crop=0&crop=1&crop=1&from=drop&id=ud39725a0&margin=%5Bobject%20Object%5D&name=ab895950-e024-4a29-a5e1-b69f24968f3e.gif&originHeight=248&originWidth=811&originalType=binary&ratio=1&rotation=0&showTitle=false&size=2301238&status=done&style=none&taskId=udb30c1eb-03e8-4eb0-abc2-8e8a045b961&title=)<br />![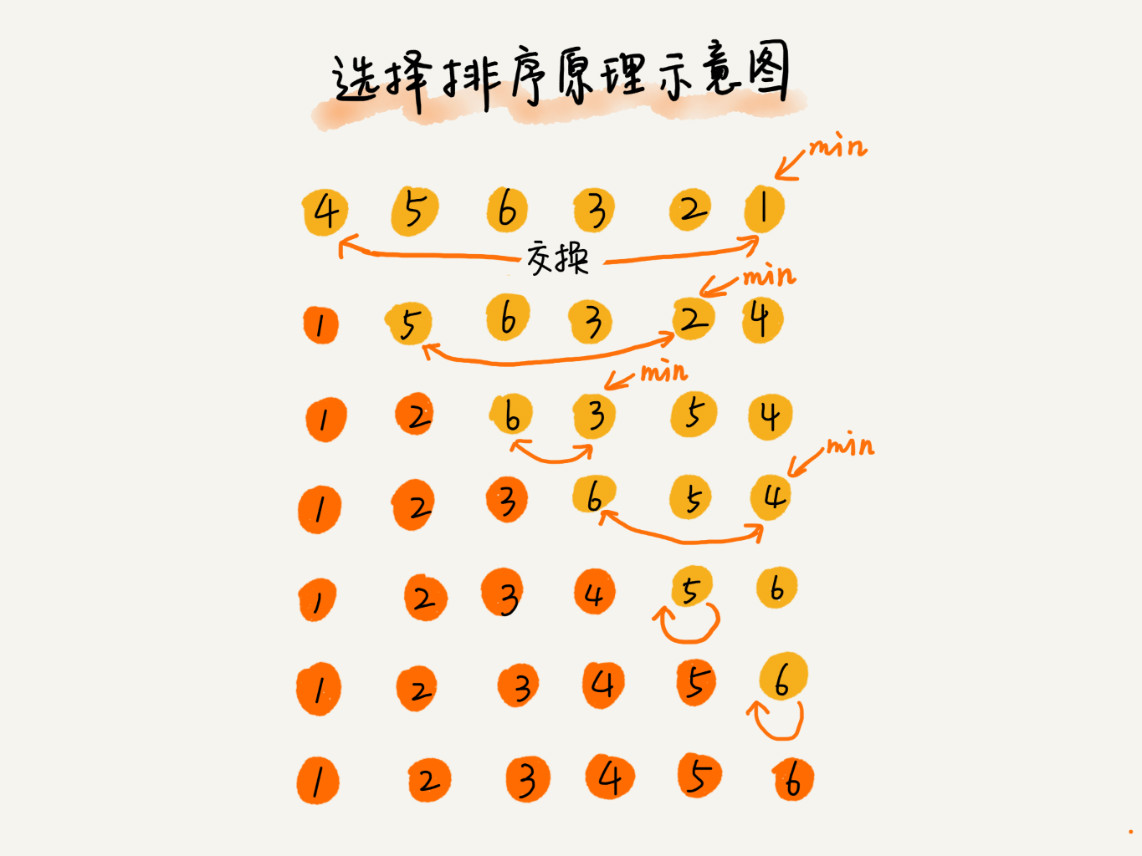image.png](https://cdn.nlark.com/yuque/0/2022/jpeg/915768/1653271820023-047bf609-b41d-46c2-a506-de30ed224d21.jpeg#clientId=u0792e8bc-9ceb-4&crop=0&crop=0&crop=1&crop=1&from=paste&id=ubf9aadb6&margin=%5Bobject%20Object%5D&name=image.png&originHeight=856&originWidth=1142&originalType=url&ratio=1&rotation=0&showTitle=false&size=128309&status=done&style=none&taskId=udfd3afe1-a6ba-42ef-9f9b-91a83428729&title=)
<a name="ASTKP"></a>
## 代码实现
两个for循环
```javascript
function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let minIndex = i
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j
      }
    }
    // 交换位置
    [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
    console.log(arr)
  }
  return arr
}
let arr = [7, 8, 9, 1, 2, 3, 4, 5, 6]
selectionSort(arr)

function selectionSort(arr) {
  let left = 0
  let right = arr.length - 1
  while (left <= right) {
    // 定义最大和最小，同时把最小的放到最前面，再把最大的放到最后面，减少内层循环
    let minIndex = left
    let maxIndex = right
    for (let i = left; i <= right; i++) {
      if (arr[i] < arr[minIndex]) {
        minIndex = i
      }
      if (arr[i] > arr[maxIndex]) {
        maxIndex = i
      }
    }
    [arr[minIndex], arr[left]] = [arr[left], arr[minIndex]]

    // 只剩最后一个的时候
    if (left == maxIndex) {
      maxIndex = minIndex
    }
    [arr[maxIndex], arr[right]] = [arr[right], arr[maxIndex]]

    console.log(arr)
    left++
    right--
  }
}

let arr = [4, 5, 6, 7, 9, 8, 2, 3, 1, 20]
selectionSort(arr)

选择排序是一种不稳定的排序算法。选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。比如 5，8，5，2，9 这样一组数据，选择排序算法第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。

function selectionSort(arr) {
  for (let i = 0; i < arr.length; ++i) {
    let minIndex = i
    for (let j = i + 1; j < arr.length; ++j) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j
      }
    }
    let minVal = arr[minIndex]
    // 解决选择排序的不稳定性，不交换，选择整体向后移动
    while (minIndex > i) {
      arr[minIndex] = arr[minIndex - 1]
      minIndex--
    }
    arr[i] = minVal
    console.log(arr)
  }
  return arr
}
let arr = [7, 8, 9, 1, 2, 3, 4, 5, 6]
selectionSort(arr)

复杂度

空间复杂度为 O(1)，是一种原地排序算法。
时间复杂度：最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2)。

冒泡、插入、选择

冒泡排序（Bubble Sort）

原理

代码实现

复杂度

插入排序（Insertion Sort）

原理

代码实现

复杂度

希尔排序

复杂度