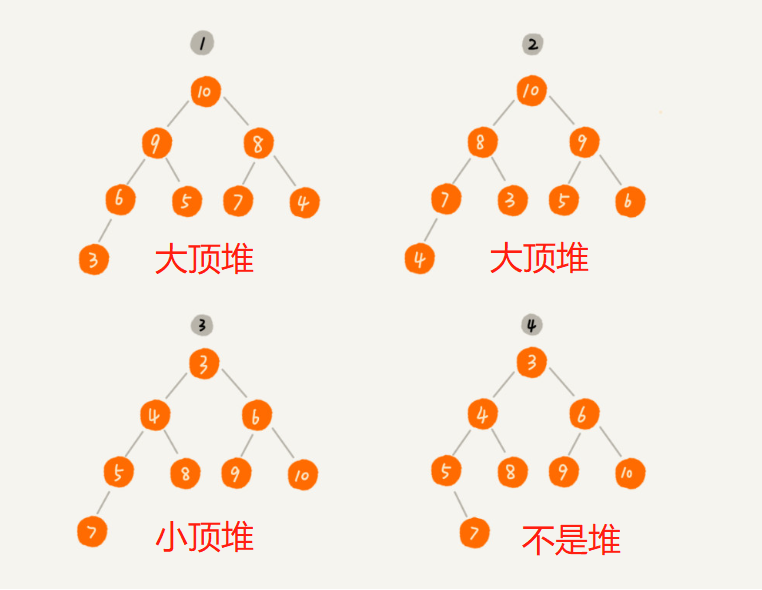
概念

堆是一种特殊的树，满足以下两点要求的树就是堆：

  • 堆是一个完全二叉树；
  • 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点（左右子节点）的值。
    • 每个节点的值都大于等于子树中每个节点值的堆，叫作“大顶堆”
    • 每个节点的值都小于等于子树中每个节点值的堆，叫作“小顶堆”。

image.png

实现堆

建立堆

完全二叉树比较适合用数组来存储。因为用数组来存储完全二叉树是非常节省存储空间的，不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。
所以对于下标为i的节点：

  • 其左子节点的下标为 i∗2
  • 其右子节点的下标为i∗2+1

  • 其父节点的下标为堆Heap - 图2

    插入操作

    堆化（heapify）：以大顶堆为例，让新插入的节点与父节点做对比，如果子节点大于父节点，就互换两个节点。一直重复这个过程，直到父节点大于等于子节点。
    image.png

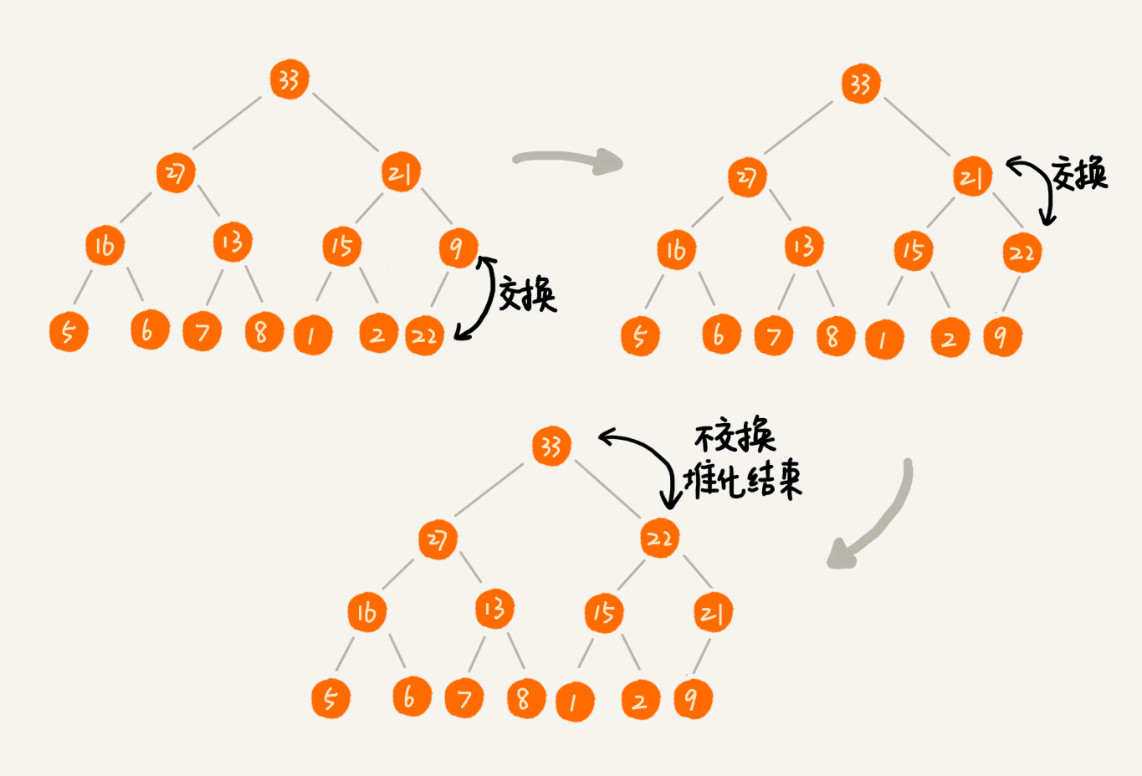
    删除堆顶操作

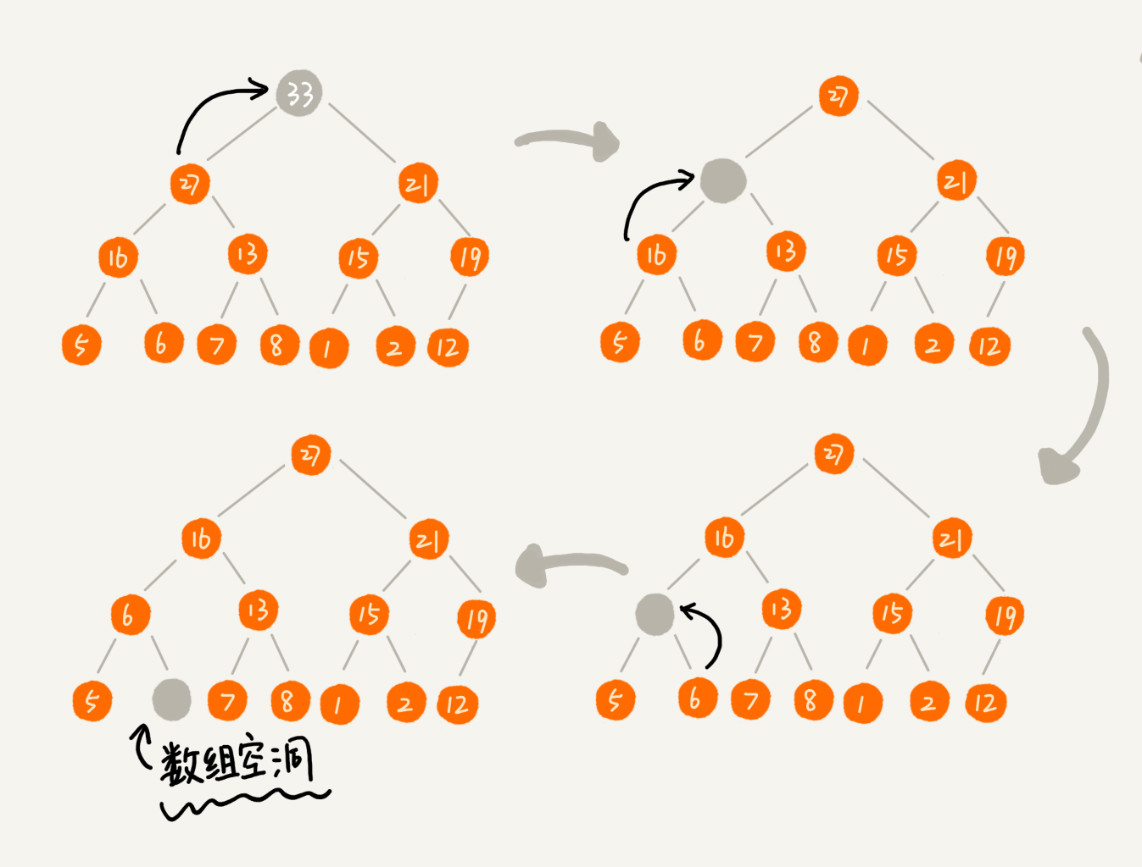
    由于堆中任何节点的值都大于等于（或小于等于）子树节点的值，所以堆顶元素就是堆中的最大值或者最小值。以大顶堆为例，堆顶元素就是最大的元素。当删除堆顶元素之后，就需要把第二大的元素放到堆顶，第二大元素肯定会出现在左右子节点中。然后再迭代地删除第二大节点，以此类推，直到叶子节点被删除。不过这种方法有点问题，就是最后堆化出来的堆并不满足完全二叉树的特性。
    image.png
    改进：把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。因为移除的是数组中的最后一个元素，而在堆化的过程中，都是交换操作，不会出现数组中的“空洞”，所以这种方法堆化之后的结果，肯定满足完全二叉树的特性。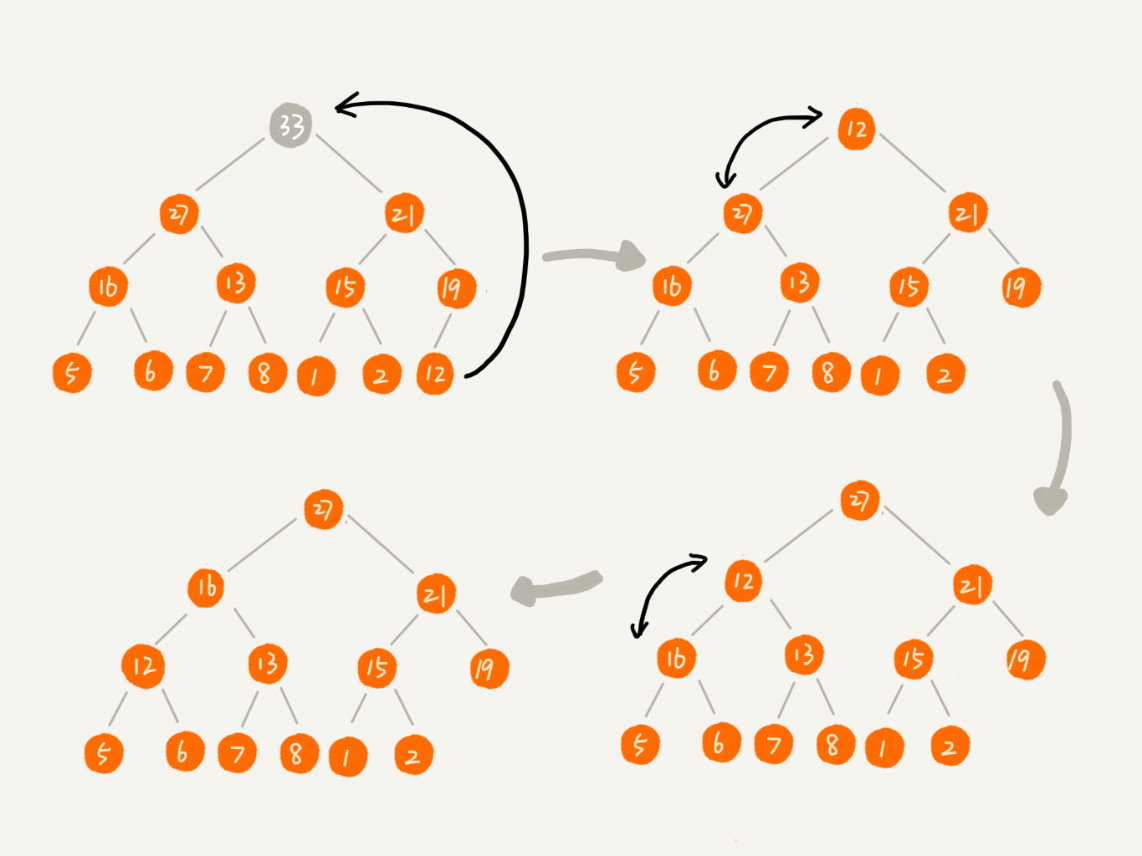
    image.png ```javascript class Heap { constructor(compare) { this.arr = [ 0 ]; // 下标从1开始好算，下标0废弃 this.compare = (typeof compare === ‘function’) ? compare : this._defaultCompare; }

    /**

    • 静态方法，可以对一组数据直接进行堆排序，原理就是将一组数据挨个push进去 */ static heapify(data, compare = undefined) { let heap = new Heap(compare); for (let item of data) { heap.push(item); } return heap; }

    /**

    • 插入，插入的同时进行堆排序 */ push(item) { let { arr, compare } = this; arr.push(item); let k = arr.length - 1 // 从下向上堆化 while (k > 1 && compare(arr[k], arr[Math.floor(k / 2)])) { this._swap(Math.floor(k / 2), k); k = Math.floor(k / 2); } }

    /**

    • 删除堆顶 */ pop() { if(this.size === 0) return null; // 行为同Java的PriorityQueue let { arr } = this; this._swap(1, arr.length - 1);// 末尾的换上来，堆顶放到最后等待返回 let res = arr.pop(); this._down(1);// 换上来的末尾，再从上到下堆化 // console.log(‘pop’, arr.slice(1)); return res; }

    /**

    • 堆中元素数量 */ get size() { return this.arr.length - 1; }

    /**

    • 返回堆顶元素 */ peek() { return this.arr[1]; }

    /**

    • 下沉第k个元素 / _down(k) { let { arr, compare } = this; let size = this.size; // 如果沉到堆底，就沉不下去了 while (k 2 <= size) { let child = k 2; let right = k 2 + 1 if (right <= size && compare(arr[right], arr[child])) { child = right; // 选择左右子节点中更靠近堆顶的，这样能维持下沉后原本的 left与right 之间的顺序关系 } // 如果当前的k比子节点更靠近堆顶，不用下沉了 if (compare(arr[k], arr[child])) return; this._swap(k, child); k = child; } }

    /**

    • 交换位置 */ _swap(i, j) { let arr = this.arr; [ arr[i], arr[j] ] = [ arr[j], arr[i] ]; }

    /**

    • a是否比b更接近堆顶，默认为小顶堆 */ _defaultCompare(a, b) { return a < b; } }

// 使用方式一：new Heap() let heap = new Heap((a,b) => { return a > b }); //大顶堆 heap.push(3); heap.push(1); heap.push(2);

heap.size; //3

heap.pop(); //3 heap.pop(); //2 heap.pop(); //1 heap.pop(); //null

// 调用方式二：Heap.heapify() let arr = [ 3, 2, 3, 1, 2, 4, 5, 5, 6 ]; let heap = Heap.heapify(arr);

while (heap.size) { console.log(heap.pop()); } ```

堆排序复杂度

堆排序是一种原地的、时间复杂度为 O(nlog⁡n) 的排序算法：

  • 整个堆排序的过程，都只需要极个别临时存储空间，所以堆排序是原地排序算法
  • 建堆过程的时间复杂度是 O(n)，排序过程的时间复杂度是 O(nlog⁡n)
  • 堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

快速排序平均情况下时间复杂度也为O(nlog⁡n)。堆排序比快速排序的时间复杂度还要稳定，但是，在实际的软件开发中，快速排序的性能要比堆排序好：

  • 第一点，堆排序数据访问的方式没有快速排序友好。快速排序数据是顺序访问的。堆排序数据是跳着访问的。 比如堆排序中的堆化。对堆顶节点进行堆化，会依次访问数组下标是 1，2，4，81，2，4，8 的元素，而不是像快速排序那样，局部顺序访问，所以，这样对 CPU 缓存是不友好的。
  • 第二点，对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。

    应用

    优先级队列

    优先级队列，首先应该是一个队列(先进先出)，不过在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。
    用堆来实现优先级队列是最直接、最高效的。往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。
    优先级队列的应用场景非常多：赫夫曼编码、图的最短路径、最小生成树算法，Java 的 PriorityQueue，C++ 的 priority_queue 等。

    1. 合并有序小文件

    有100 个小文件，每个文件的大小是 100MB，每个文件中存储的都是有序的字符串。将这些 100 个小文件合并成一个有序的大文件。这里就会用到优先级队列。
    整体思路有点像归并排序中的合并函数。从这 100 个文件中，各取第一个字符串，放入数组中，然后比较大小，把最小的那个字符串放入合并后的大文件中，并从数组中删除。假设，这个最小的字符串来自于 13.txt 这个小文件，就再从这个小文件取下一个字符串，并且放到数组中，重新比较大小，并且选择最小的放入合并后的大文件，并且将它从数组中删除。依次类推，直到所有的文件中的数据都放入到大文件为止。
    利用优先级队列，将从小文件中取出来的字符串放入到小顶堆中，那堆顶的元素，也就是优先级队列队首的元素，就是最小的字符串。将这个字符串放入到大文件中，并将其从堆中删除。然后再从小文件中取出下一个字符串，放入到堆中。循环这个过程，就可以将 100 个小文件中的数据依次放入到大文件中。

    2. 高性能定时器

    有一个定时器中维护了很多定时任务，每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间（比如 1 秒），就扫描一遍任务，看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。但是每过 1 秒就扫描一遍任务列表的做法比较低效，主要原因有两点：第一，任务的约定执行时间离当前时间可能还有很久，这样前面很多次扫描其实都是徒劳的；第二，每次都要扫描整个任务列表，如果任务列表很大的话，势必会比较耗时。
    利用优先级队列按照任务设定的执行时间，将这些任务存储在优先级队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。这样，定时器就不需要每隔 1 秒就扫描一遍任务列表了。它拿队首任务的执行时间点，与当前时间点相减，得到一个时间间隔 T。这时定时器就可以设定在 T 秒之后，再来执行任务。从当前时间点到（T-1）秒这段时间里，定时器都不需要做任何事情。
    当 T 秒时间过去之后，定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值，把这个值作为定时器执行下一个任务需要等待的时间。定时器既不用间隔 1 秒就轮询一次，也不用遍历整个任务列表，性能也就提高了。

    求 Top K

    求 Top K 的问题抽象成两类：一类是针对静态数据集合，即数据集合事先确定，不会再变。另一类是针对动态数据集合，即数据集合事先并不确定，有数据动态地加入到集合中。
    针对静态数据，如何在一个包含 n 个数据的数组中，查找前 K 大数据呢？可以维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出取数据与堆顶元素比较。如果比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理，继续遍历数组。这样等数组中的数据都遍历完之后，堆中的数据就是前 K 大数据了。
    针对动态数据求得 Top K 就是实时 Top K。如果每次询问前 K 大数据，可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，就拿它与堆顶的元素对比。如果比堆顶元素大，就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。这样，无论任何时候需要查询当前的前 K 大数据，都可以里立刻返回给他。

    求中位数

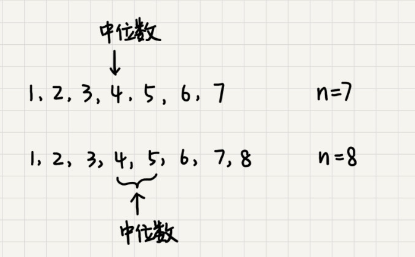
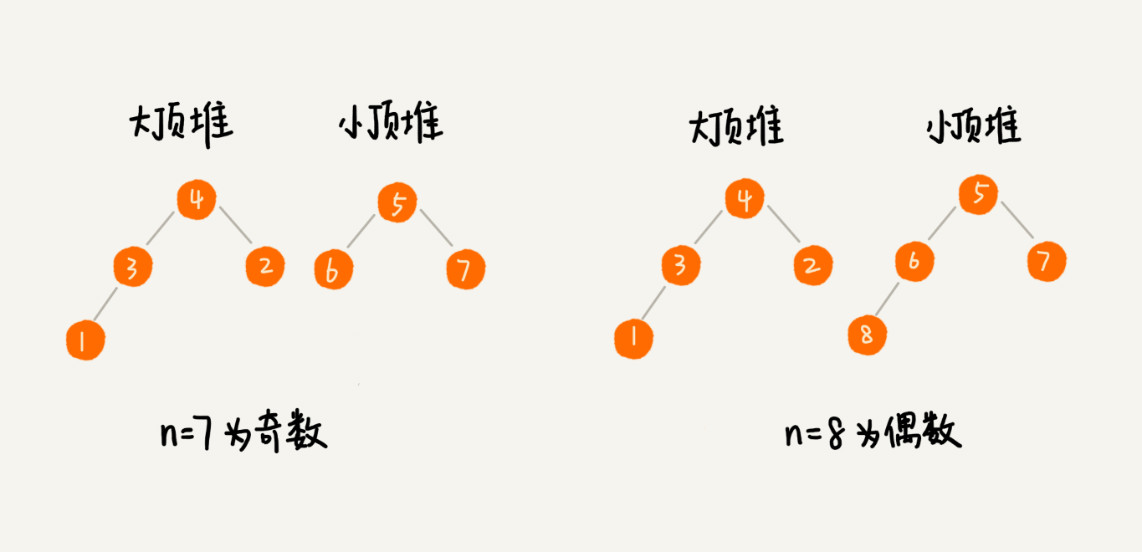
    image.png
    借助堆，不用排序，就可以非常高效地求出中位数：维护两个堆，一个大顶堆，一个小顶堆。大顶堆中存储前半部分数据，小顶堆中存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。
    有 n 个数据，n 是偶数，从小到大排序，那前堆Heap - 图7个数据存储在大顶堆中，后 堆Heap - 图8 个数据存在小顶堆中。大顶堆中的堆顶元素就是中位数。如果 n 是奇数，大顶堆存 堆Heap - 图9+1 个数据，小顶堆中存 堆Heap - 图10 个数据。
    image.png
    如果新加入的数据小于等于大顶堆的堆顶元素，就将这个新数据插入到大顶堆；如果新加入的数据大于等于小顶堆的堆顶元素，就将这个新数据插入到小顶堆。同时要进行调整：从一个堆中不停地将堆顶元素移动到另一个堆中，以保证大小顶堆数据的个数满足上面的约定。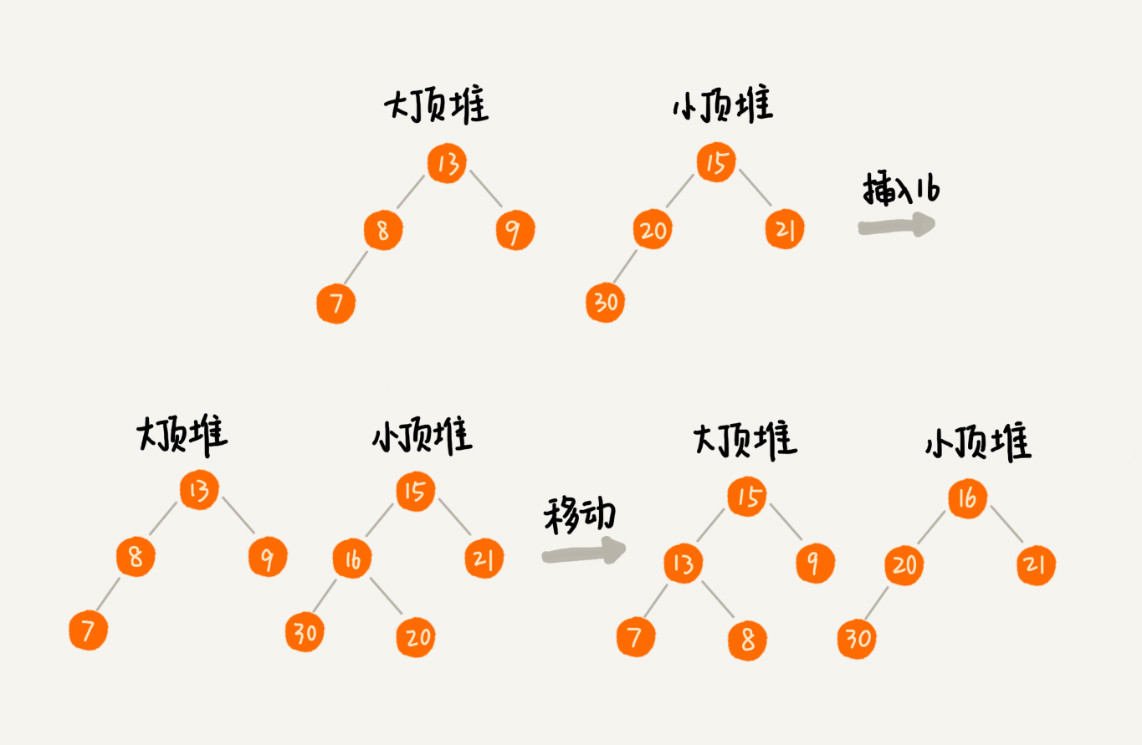
    image.png
    实际上，利用两个堆不仅可以快速求出中位数，还可以快速求其他百分位的数据，“如何快速求接口的 99% 响应时间？”，如果将一组数据从小到大排列，这个 99 百分位数就是大于前面 99% 数据的那个数据。
    维护两个堆，一个大顶堆，一个小顶堆。假设当前总数据的个数是 n，大顶堆中保存 n99% 个数据，小顶堆中保存 n1% 个数据。大顶堆堆顶的数据就是要找的 99% 响应时间。
    每次插入一个数据的时候，都要判断这个数据跟大顶堆和小顶堆堆顶数据的大小关系，然后决定插入到哪个堆中。但是，为了保持大顶堆中的数据占 99%，小顶堆中的数据占 1%，在每次新插入数据之后，都要重新计算大顶堆和小顶堆中的数据个数，是否还符合 99:1 这个比例。如果不符合，就将一个堆中的数据移动到另一个堆，直到满足这个比例。