几乎所有的编程语言都原生支持数组类型，它不仅仅是一种编程语言中的数据类型，还是一种最基础最简单的内存数据结构。

数组的定义

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。
两个关键特性：第一是线性表（Linear List）。顾名思义，线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。image.png
与之相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。
image.png
第二是连续的内存空间和相同类型的数据。
正因为有上述两个特性，所以数组才有“随机访问”的特性。有利就有弊，这也限制了数组的很多操作变得非常低效，比如要想在数组中删除、插入一个数据，为了保证连续性，就需要做大量的数据搬移工作。

  • JS里的数组添加元素会自动扩容，不需要手动扩容；其它语言（如C和Java）需要手动进行动态扩容，比如创建一个全新的数组进行数据搬移
  • JavaScript只支持一维数组，并不支持矩阵；但是可以通过数组嵌套来实现矩阵和任一多维数组，通过console.table(二维数组)会显示一个更加友好的输出结果。

数组的存储与随机访问

定义一个长度为 10 的 int 类型的数组 int[] a = new int[10] 。计算机给数组 a，分配了一块连续内存空间 1000～1039，其中，内存块的首地址为 base_address = 1000。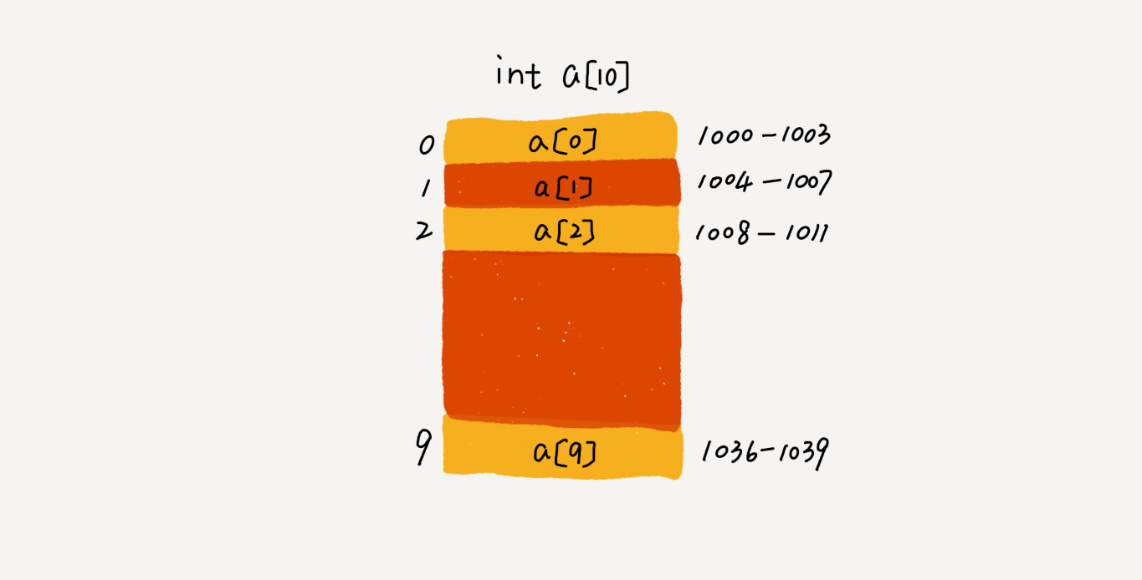
image.png
计算机会给每个内存单元分配一个地址，计算机通过地址来访问内存中的数据。当计算机需要随机访问数组中的某个元素时，它会首先通过寻址公式**a[i]_address = base_address + i * data_type_size**，计算出该元素存储的内存地址。data_type_size 表示数组中每个元素的大小，int 类型数据的data_type_size 就为 4 个字节。数组是适合查找操作，但是查找的时间复杂度并不为 O(1)。即便是排好序的数组，用二分查找，时间复杂度也是 O(logn)。所以，正确的表述应该是，数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)。

数组的插入与删除

数组为了保持内存数据的连续性，会导致插入、删除这两个操作比较低效。

插入

假设一个长度为n的有序数组，现在需要将一个数据插入到数组中的第 k 个位置。如果在数组的末尾插入元素，那就不需要移动数据了，这是最好的时间复杂度为 O(1)。但如果在数组的开头插入元素，那所有的数据都需要依次往后移动一位，所以最坏时间复杂度是 O(n)。因为在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为 (1+2+…n)/n=O(n)。
但如果是无序数组，只需要直接将第 k 位的数据搬移到数组元素的最后，把新的元素直接放入第 k 个位置。这样时间复杂度就会降为 O(1)，这种思想也是快排。

删除

同理，要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。如果删除数组末尾的数据，则最好情况时间复杂度为 O(1)；如果删除开头的数据，则最坏情况时间复杂度为 O(n)；平均情况时间复杂度也为 O(n)。
实际上，并不一定非得追求数组中数据的连续性。如果将多次删除操作集中在一起执行，删除的效率会提高很多：比如依次删除下面的 a，b，c 三个元素，为了避免 d，e，f，g，h 这几个数据会被搬移三次，我们可以先记录下已经删除的数据，每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。（JVM 标记清除垃圾回收算法的核心思想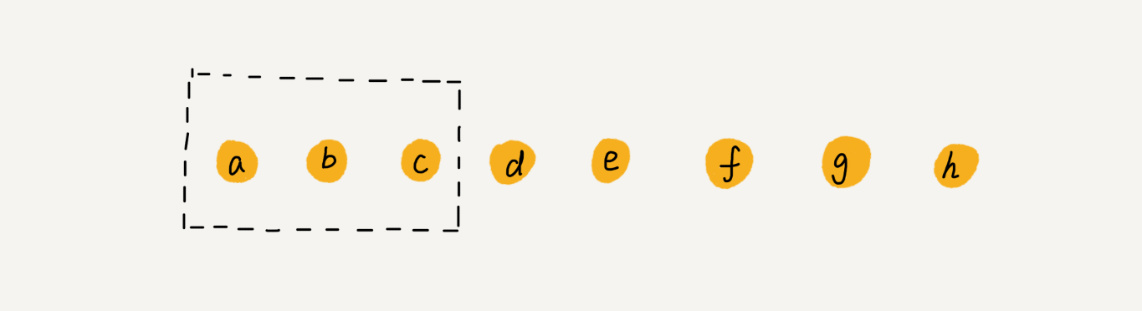）image.png

数组的访问越界问题

  1. int main(int argc, char* argv[]){
  2.     int i = 0;
  3.     int arr[3] = {0};
  4.     for(; i<=3; i++){ // 当 i=3 时，数组 a[3] 访问越界
  5.         arr[i] = 0;
  6.         printf("hello world\n"); // 运行结果并非是打印三行“hello word”，而是会无限打印“hello world”
  7.     }
  8.     return 0;
  9. }

在 C 语言中，只要不是访问受限的内存，所有的内存空间都是可以自由访问的。根据数组寻址公式，a[3] 也会被定位到某块不属于数组的内存地址上，而这个地址正好是存储变量 i 的内存地址，那么 a[3]=0 就相当于 i=0，所以就会导致代码无限循环。
数组越界在 C 语言中是一种未决行为，并没有规定数组访问越界时编译器应该如何处理。因为，访问数组的本质就是访问一段连续内存，只要数组通过偏移计算得到的内存地址是可用的，那么程序就可能不会报任何错误。这种情况下，一般都会出现莫名其妙的逻辑错误，这种情况下，一般都会出现莫名其妙的逻辑错误，很多计算机病毒也正是利用到了代码中的数组越界可以访问非法地址的漏洞，来攻击系统，所以写代码的时候一定要警惕数组越界。
但并非所有的语言都像 C 一样，把数组越界检查的工作丢给程序员来做，像 Java 本身就会做越界检查，越界就会抛出java.lang.ArrayIndexOutOfBoundsException

容器能否完全替代数组？

针对数组类型，很多语言都提供了容器类，比如 Java 中的 ArrayList、C++ STL 中的 vector。

  1. 对于业务开发，直接使用容器，省时省力。如果是做一些非常底层的开发，比如开发网络框架，性能的优化需要做到极致，这个时候数组就会优于容器，成为首选。
  2. Java ArrayList 无法存储基本类型，比如 int、long，需要封装为 Integer、Long 类，而 Autoboxing、Unboxing 则有一定的性能消耗，所以如果特别关注性能，或者希望使用基本类型，就可以选用数组。
  3. 如果数据大小事先已知，并且对数据的操作非常简单，用不到 ArrayList 提供的大部分方法，也可以直接使用数组。

    数组为什么从 0 开始编号

    从数组存储的内存模型上来看，“下标”最确切的定义应该是“偏移（offset）”。如a[0] 就是偏移为 0 的位置，也就是首地址，a[k] 就表示偏移 k 个 type_size 的位置，所以计算 a[k] 的内存地址公式：a[k]_address = base_address + k * type_size
    但是，如果数组从 1 开始计数，那计算数组元素 a[k] 的内存地址公式就会变为：a[k]_address = base_address + (k-1)*type_size。
    对比两个公式，从 1 开始编号，每次随机访问数组元素都多了一次减法运算，对于 CPU 来说，就是多了一次减法指令。数组作为非常基础的数据结构，通过下标随机访问数组元素又是其非常基础的编程操作，效率的优化就要尽可能做到极致。所以为了减少一次减法操作，数组选择了从 0 开始编号，而不是从 1 开始。
    但其实最主要的原因可能是历史原因，C 语言设计者用 0 开始计数数组下标，之后的 Java、JavaScript 等高级语言都效仿了 C 语言，或者说，为了在一定程度上减少 C 语言程序员学习 Java 的学习成本，因此继续沿用了从 0 开始计数的习惯。实际上，很多语言中数组也并不是从 0 开始计数的，比如 Matlab。甚至还有一些语言支持负数下标，比如 Python。

    应用

    求斐波那契数列的前20个数

    const fibonacci = []; 
fibonacci[1] = 1; // 因为斐波那契数列中不存在0，所以这里直接从第二位开始
fibonacci[2] = 1; // 斐波那契数列中的前两项是1
for (let i = 3; i < 20; i++) {
fibonacci[i] = fibonacci[i -1] + fibonacci[i -2]; // 斐波那契数列公式，从第三个开始，当前项=前两项之和
}
console.log(fibonacci); // [空, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

    模拟unshift、shift

    unshift：在数组的开头中插入一个新元素，首先要腾出数组里第一个元素的位置，把所有的元素向右移动一位。可以循环数组中的元素，从最后一位（长度值就是数组的末尾位置）开始，将对应的前一个元素（i-1）的值赋给它（i），依次处理，最后把想要的值赋给第一个位置（索引0）上。
    // unshift方法背后的逻辑和insertFirstPosition方法的行为是一样的
// 但是unshift还支持一次插入多个，numbers.unshift(-4, -3)，暂时没有实现，但是也挺简单
Array.prototype.insertFirstPosition = function(value) {
for (let i = this.length; i >= 0; i--) {
 this[i] = this[i -1];
}
this[0] = value;
};
numbers.insertFirstPosition(-1);
    shift：移除数组里的第一个元素，并且修改原数组的长度
    Array.prototype.removeFirstPosition = function() {
for (let i = 0; i < this.length; i++) {
 this[i] = this[i + 1]; // 移除的原理就是后一个覆盖前一个值，但是这会导致数组最后一个值为undefined
}
// 所以需要处理最后一个值
this.length--
return this
};
numbers = numbers.removeFirstPosition();