栈数据结构

栈是一种遵从后进先出（LIFO）原则的有序集合。新添加或待删除的元素都保存在栈的同一端，称作栈顶，另一端就叫栈底。在栈里，新元素都靠近栈顶，旧元素都接近栈底。一个非常贴切的例子就是一摞叠在一起的盘子。放盘子的时候，都是从下往上一个一个放；取的时候，也是从上往下一个一个地依次取，不能从中间任意抽出。

栈的基本操作：入栈和出栈，只允许在一端插入和删除数据，栈是一种“操作受限”的线性表数据结构。
从功能上来说，数组或链表确实可以替代栈，但是栈这种特定的数据结构针对特定的场景：当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，就应该首选“栈”这种数据结构。

JS实现一个“栈”

栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈叫作顺序栈，用链表实现的栈叫作链式栈。

数组实现顺序栈

通过push和pop方法，就能用数组来模拟栈；
注意：如果入栈是放在数组最后，那么出栈也是先取数组最后的；如果入栈是放在数组最前，那么出栈也要取数组最前的；必须要在栈的一端进行操作

// 定义栈类（纯粹是用数组的属性和方法来模拟栈）
class StackArray {
  constructor() {
    this.items = []
  }
  // 入栈
  push(item) {
    this.items.push(item) // 放在最后
  }
  // 出栈（移除栈顶元素，同时返回被删除的元素）
  pop() {
    return this.items.pop();
  }
  // 返回栈顶元素值,不对栈做任何修改
  peek() {
    return this.items[this.items.length - 1];
  }
  // 判断栈是否为空
  isEmpty() {
    return this.items.length === 0
  }
  // 返回给定对象的位置
  search(item) {
    let index = this.items.lastIndexOf(item)
    if (index >= 0) {
      return this.size() - index
    } else {
      return -1
    }
  }
  // 获取栈元素个数
  size() {
    return this.items.length
  }
  // 清空栈
  clear() {
    this.items = []
  }
  toString() {
    return this.items.toString();
  }
}
// 测试
const stack = new StackArray()
console.log(stack.isEmpty()) // true
stack.push('nodeA') 
stack.push('nodeB')
stack.push('nodeC')
while (!stack.isEmpty()) {
  console.log(stack) 
  stack.pop()
}
// Stack { items: [ 'nodeA', 'nodeB', 'nodeC' ] }
// Stack { items: [ 'nodeA', 'nodeB' ] }
// Stack { items: [ 'nodeA' ] }

利用数组实现的栈，内部的数组items并不是私有属性，不受保护，可以利用WeakMap来实现私有属性：

const items = new WeakMap() // 声明一个WeakMap类型的变量items
class Stack {
  constructor() {
    items.set(this, []) // 以this（Stack类自己的引用）为键，把代表栈的数组存入items
    // ⭐items在Stack类里是真正的私有属性。采用这种方法，代码的可读性不强，而且在扩展该类时无法继承私有属性
  }
  push(element) {
    const s = items.get(this) // 从WeakMap中取出值，即以this为键从items中取值。
    s.push(element)
  }
  pop() {
    const s = items.get(this)
    const r = s.pop()
    return r
  }
  // 其他方法
}

对象实现栈

class Stack {
  constructor() {
    this.count = 0 // 记录栈的大小
    this.items = {} 
  }
  // 数组实现的栈可以一次添加多个元素。但是对象，只允许一次插入一个元素
  push(element) {
    this.items[this.count] = element // 放在最后
    this.count++ // 插入元素后，递增count变量
  }
  // 对象，通过delete来删除
  pop() {
    if (this.isEmpty()) {
      return undefined
    }
    this.count--
    const result = this.items[this.count]
    delete this.items[this.count] // 删除最后
    return result
  }
  peek() {
    if (this.isEmpty()) {
      return undefined
    }
    return this.items[this.count - 1] // 获取栈顶元素
  }
  isEmpty() {
    return this.count === 0
  }
  size() {
    return this.count
  }
  clear() {
    /* while (!this.isEmpty()) {
        this.pop();
      } */
    this.items = {}
    this.count = 0
  }
  toString() {
    if (this.isEmpty()) {
      return ''
    }
    let objString = `${this.items[0]}`
    for (let i = 1; i < this.count; i++) {
      objString = `${objString},${this.items[i]}`
    }
    return objString
  }
}
// 测试
const stack = new Stack()
stack.push(5)
stack.push(8)
console.log(stack) // Stack { count: 2, items: { '0': 5, '1': 8 } }

栈操作的复杂度

空间复杂度：不管是顺序栈还是链式栈，存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。注意：存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n)。因为，这 n 个空间是必须的，无法省掉。所以说空间复杂度的时候，是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。
时间复杂度：不管是顺序栈还是链式栈，入栈、出栈只涉及栈顶数据的操作，所以时间复杂度都是 O(1)。

栈的应用

浏览器前进后退

使用两个栈X 和 Y，把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈 X 中出栈，并将出栈的数据依次放入栈 Y。当点击前进按钮时，依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。比如顺序查看了 a，b，c 三个页面，就依次把 a，b，c 压入栈，此时两个栈的数据如下图：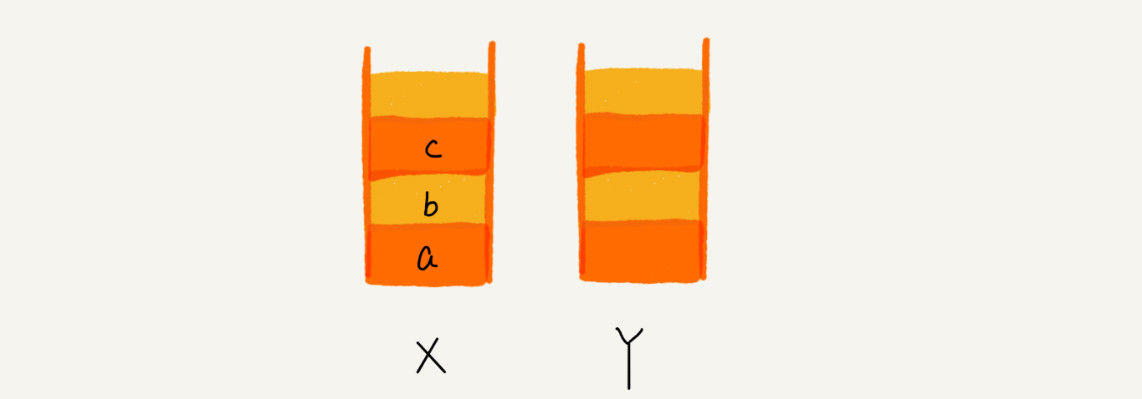

当点击后退按钮，从页面 c 后退到页面 a 之后，就依次把 c 和 b 从栈 X 中弹出，并且依次放入到栈 Y：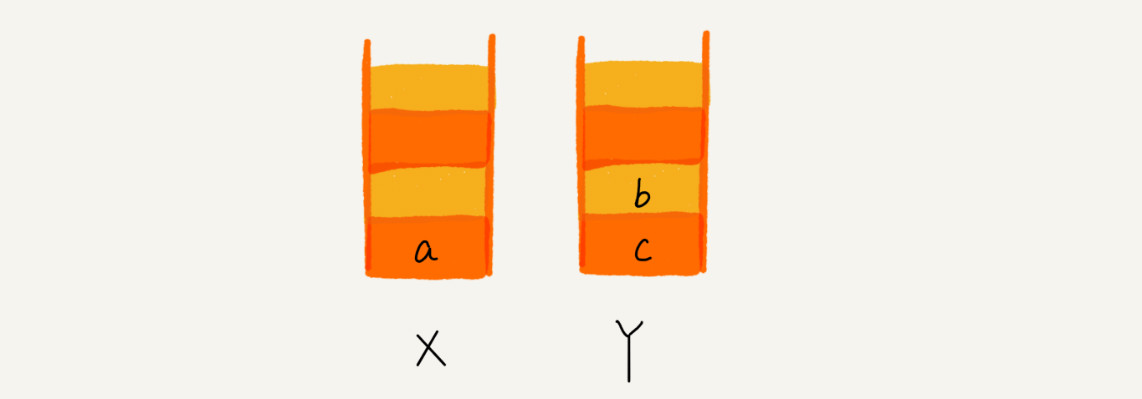

这时再点击前进按钮回到 b 页面，就把 b 再从栈 Y 中出栈，放入栈 X 中：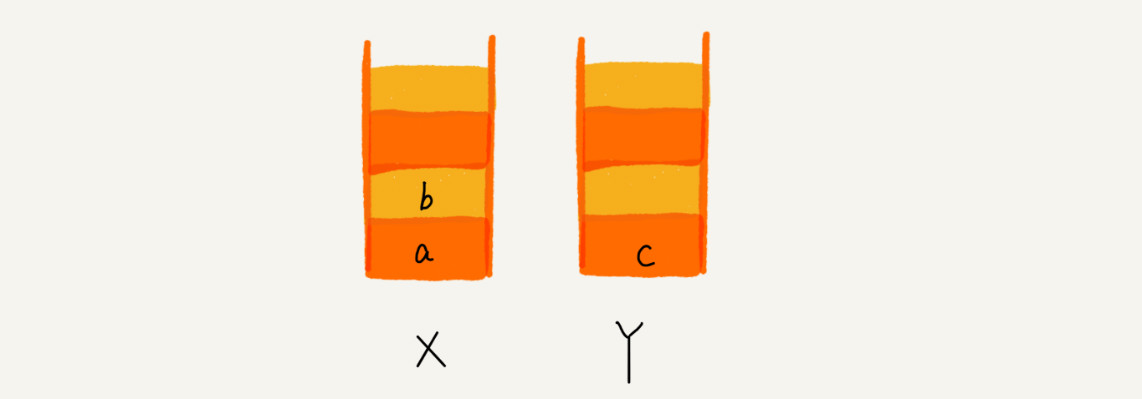

这时如果从页面 b 又跳转到新的页面 d 了，页面 c 就无法再通过前进、后退按钮重复查看了，所以需要清空栈 Y。此时两个栈的数据这个样子：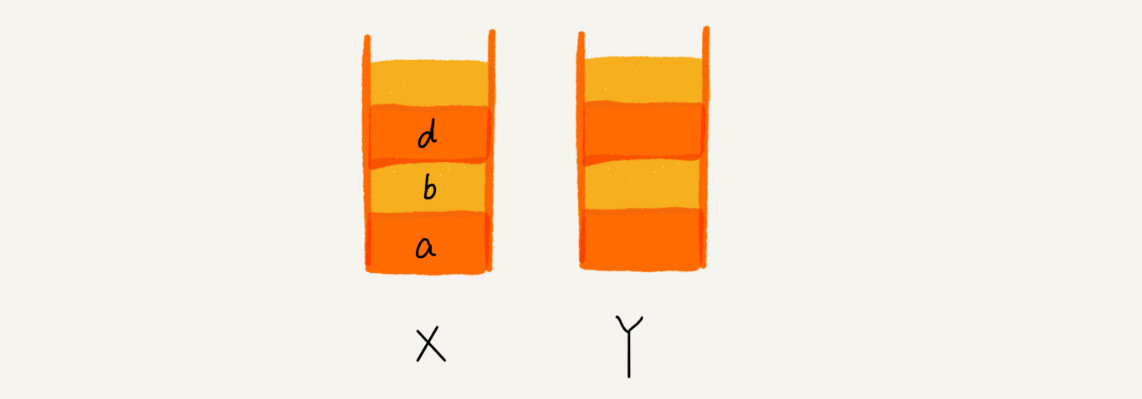

函数调用栈

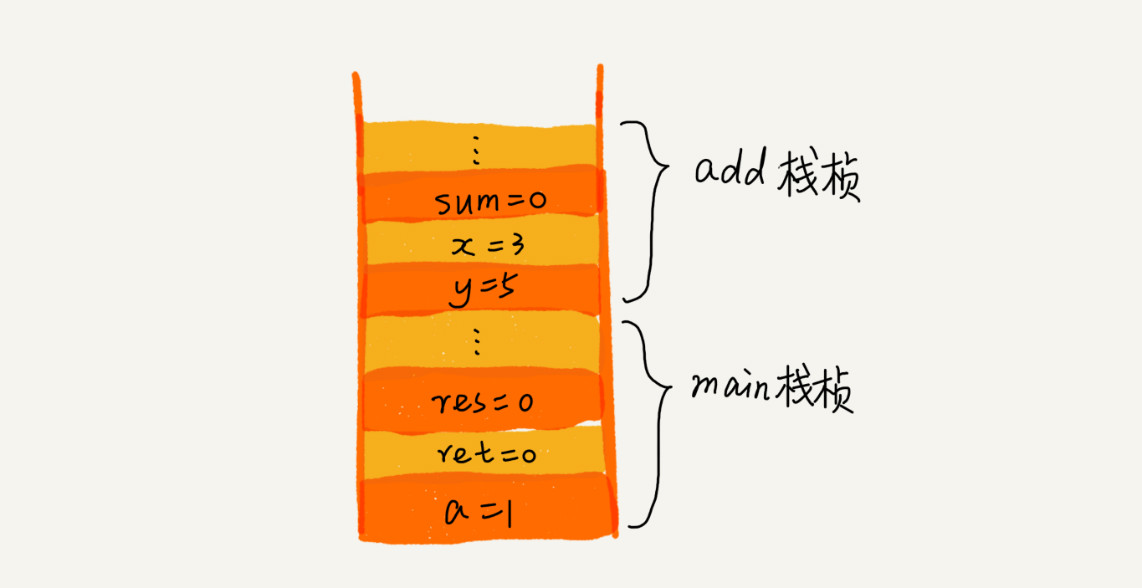
操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧压入栈，当被调用函数执行完成之后，将这个函数对应的栈帧出栈。

int main() {
   int a = 1; 
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

表达式求值

实现一个四则运算表达式求值的功能：3+5*8-6
编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。从左向右遍历表达式，当遇到数字，直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。
如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。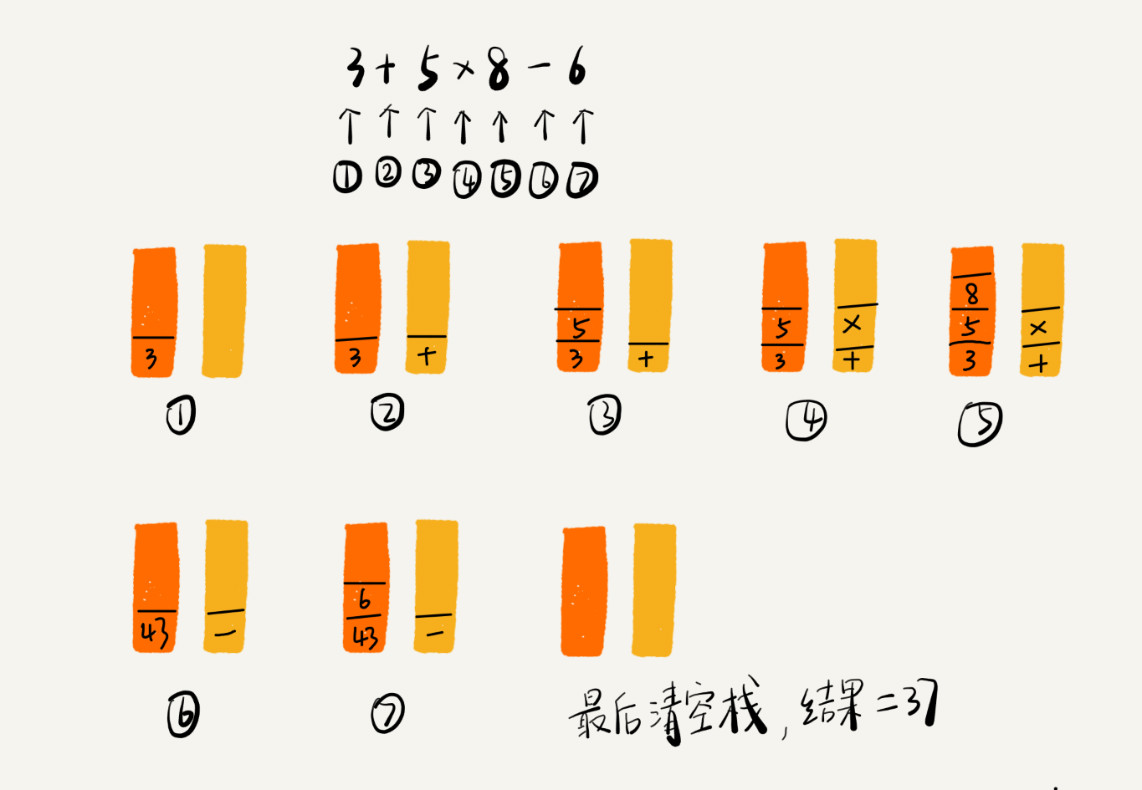

括号匹配

场景：假设表达式中只包含三种括号，圆括号 ()、方括号 [ ] 和花括号{ }，并且它们可以任意嵌套。比如，{ [ { } ] }或 [ { ( ) } ( [ ] ) ] 等都为合法格式，而{ [ } ( ) ] 或 [ ( { ) ] 为不合法的格式。那如何检查它是否合法？
解决：可以用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。
当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

十进制转换其它进制

要把十进制转化成二进制，可以将该十进制数除以2（二进制是满二进一）并对商取整，直到结果是0为止

function decimalToBinary(decNumber) {
  const remStack = new Stack()
  let number = decNumber
  let rem
  let binaryString = ''
  while (number > 0) { // 先循环将余数推入栈中
    rem = Math.floor(number % 2)
    remStack.push(rem)
    number = Math.floor(number / 2)
  }
  while (!remStack.isEmpty()) {
    binaryString += remStack.pop().toString()
  }
  return binaryString
}

// 测试
console.log(decimalToBinary(233)) // 11101001

function baseConverter(decNumber, base) {
  const remStack = new Stack()
  const digits = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ' // 三十六进制以内转换表，从十一进制开始，字母表中的每个字母将表示相应的基数
  let number = decNumber
  let rem
  let baseString = ''
  if (!(base >= 2 && base <= 36)) {
    return ''
  }
  while (number > 0) {
    rem = Math.floor(number % base)
    remStack.push(rem)
    number = Math.floor(number / base)
  }
  while (!remStack.isEmpty()) {
    baseString += digits[remStack.pop()] // 弹出表中对应的基数，主要是针对十一进制以上要用字母表示
  }
  return baseString
}

// 测试
console.log(baseConverter(100345, 8)) // 303771
console.log(baseConverter(100345, 16)) // 187F9