概述

递归的思想是将大问题分解为小问题来求解，然后再将小问题分解为小小问题。这样一层一层地分解，直到问题的数据规模被分解得足够小，不用继续递归分解为止。
将这种一层层分解的过程画成图，其实就是一棵树：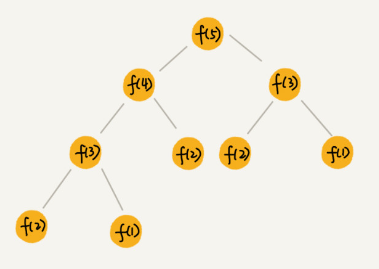

递归树的作用：借助递归树来分析递归算法的时间复杂度。

递归树求解算法时间复杂度

分析归并排序

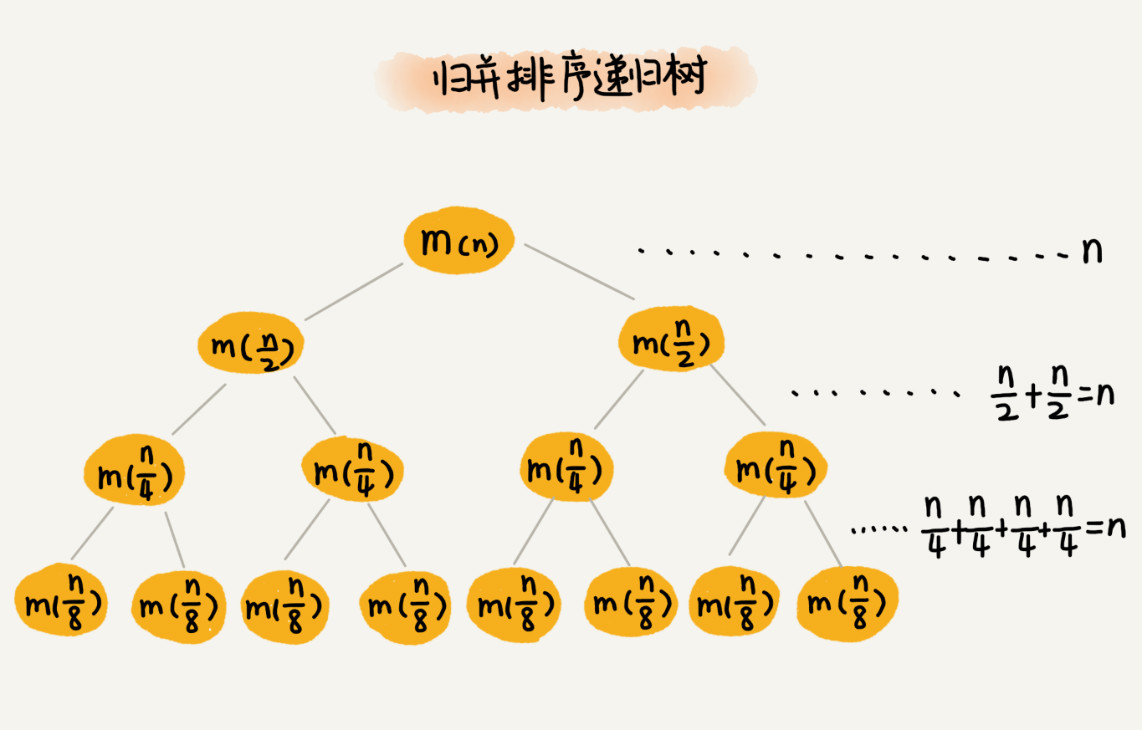
因为每次分解都是一分为二，所以代价很低，把时间上的消耗记作常量 1。归并算法中比较耗时的是归并操作，也就是把两个子数组 合并为大数组。从图中可看出，每一层归并操作消耗的时间总和是一样的，跟要排序的数据规模有关。把每一层归并操作消耗的时间记作 n。
现在，我们只需要知道这棵树的高度 h，用高度 h 乘以每一层的时间消耗 n，就可以得到总的时间复杂度 O(n∗h)。归并排序递归树是一棵满二叉树，满二叉树的高度大约是 log2n，所以，归并排序递归实现的时间复杂度就是 O(nlogn)。这里的时间复杂度都是估算的，对树的高度的计算也没有那么精确，但这并不影响复杂度的计算结果。

分析快速排序

快速排序在最好情况下，每次分区都能一分为二，这个时候用递推公式 T(n)=2T(n/2)+n，很容易就能推导出时间复杂度是 O(nlogn)。但是并不可能每次分区都正好一分为二。
假设平均情况下，每次分区之后，两个分区的大小比例为 1:k。当 k=9 时（一个分区是另一个分区的 9 倍），如果用递推公式的方法来求解时间复杂度的话，递推公式就写成 T(n)=T(n/10)+T(9n/10)+n。这个公式可以推导出时间复杂度，但是推导过程非常复杂。所以还是用递归树来求解：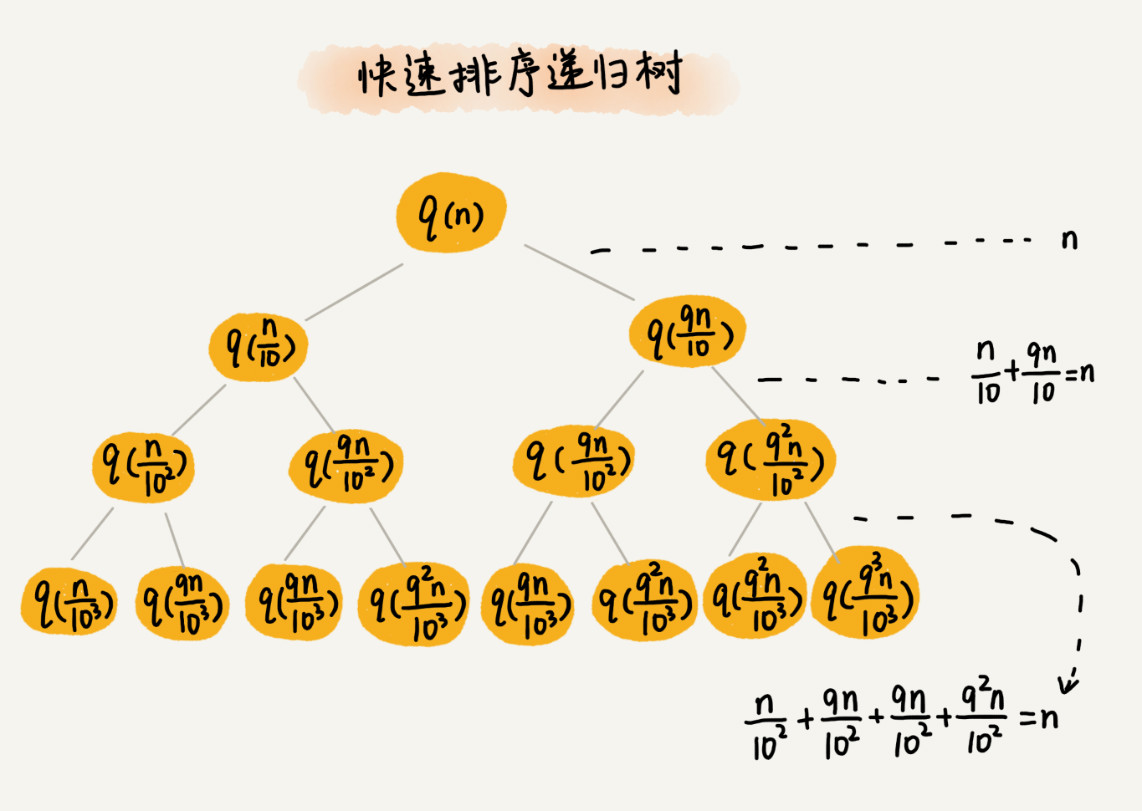

快速排序的过程中，每次分区都要遍历待分区区间的所有数据，所以，每一层分区操作所遍历的数据的个数之和就是 n。只要求出递归树的高度 h，这个快排过程遍历的数据个数就是 h∗n ，也就是说，时间复杂度就是 O(h∗n)。因为每次分区并不是均匀地一分为二，所以递归树并不是满二叉树。快速排序结束的条件就是待排序的小区间，大小为 1，也就是说叶子节点里的数据规模是 1。从根节点 nn到叶子节点 1，递归树中最短的一个路径每次都乘以 1/10，最长的一个路径每次都乘以 9/10。从根节点到叶子节点的最短路径是 log10n，最长的路径是 log10/9n。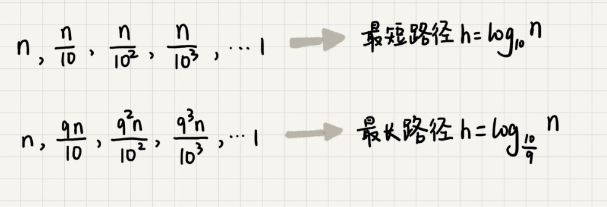
所以，遍历数据的个数总和就介于 nlog10n和 nlog10/9n之间。根据大 O 表示法，对数复杂度的底数不管是多少，统一为 logn，所以，当分区大小比例是 1:9时，快速排序的时间复杂度仍然是 O(nlogn)。
那如果 k=99，也就是说，每次分区极其不平均，两个区间大小是 1:99，树的最短路径就是 log100n，最长路径是 log100/99n，所以总遍历数据个数介于 nlog100n和 nlog100/99n之间。尽管底数变了，但是时间复杂度也O(nlogn)。
也就是说，对于 k，只要 k的值不随 n 变化，是一个确定的常量，那快排的时间复杂度就是 O(nlogn)。所以，从概率论的角度来说，快排的平均时间复杂度就是 O(nlogn)。

分析斐波那契数列

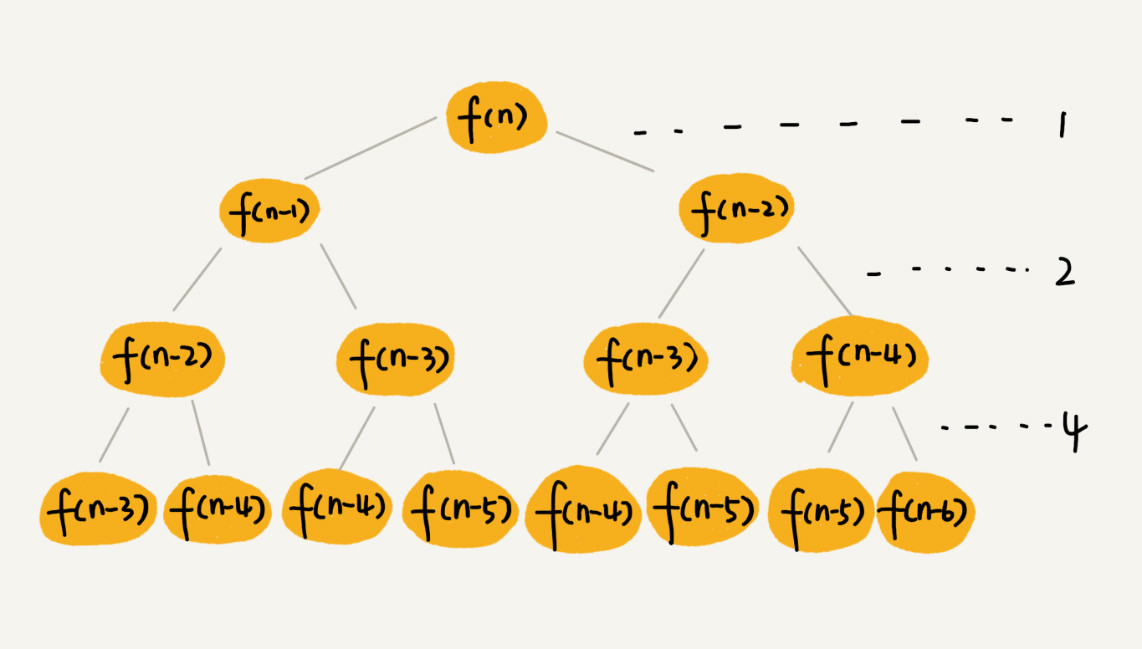
f(n) 分解为 f(n−1) 和 f(n−2)，每次数据规模都是 −1 或者 −2，叶子节点的数据规模是 1或者 2。所以，从根节点走到叶子节点，每条路径是长短不一的。如果每次都是 −1，那最长路径大约就是 n；如果每次都是 −2，那最短路径大约就是 。
每次分解之后的合并操作只需要一次加法运算，把每次加法运算的时间消耗记作 1。所以，从上往下，第一层的总时间消耗是 1，第二层的总时间消耗是 2，第三层的总时间消耗就是 22。依次类推，第 k 层的时间消耗就是 2k−1，那整个算法的总的时间消耗就是每一层时间消耗之和。
如果路径长度都为 n，那总和就是 2n −1。如果路径长度都是，那整个算法的总的时间消耗就是 2n/2−1。所以，这个算法的时间复杂度就介于 O(2n)和 O(2n/2)之间。虽然结果还不够精确，只是一个范围，但是也基本上知道了上面算法的时间复杂度是指数级的，非常高。

分析全排列

高中的时候学过排列组合。“如何把 n 个数据的所有排列都找出来”，这就是全排列的问题。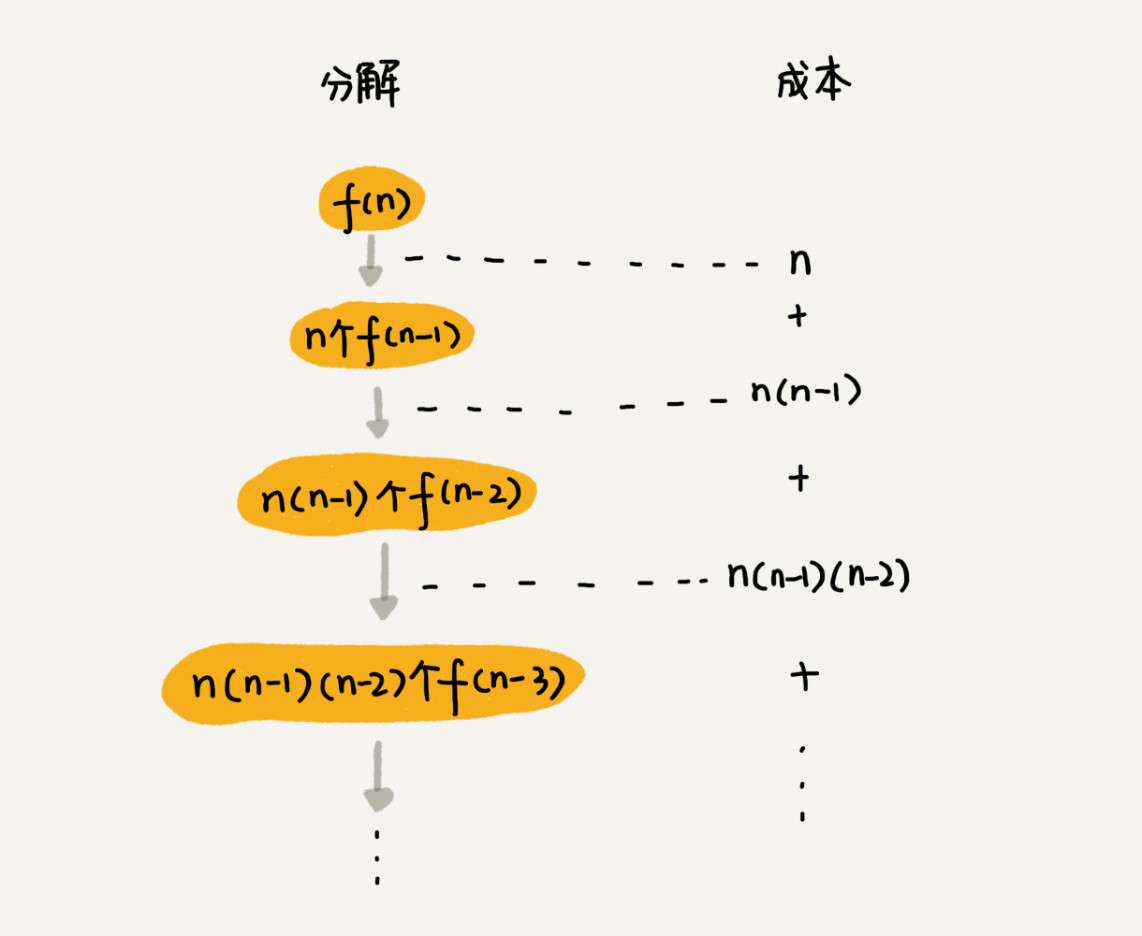

求和：n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1，总和肯定小于 n∗n!，也就是说，全排列的递归算法的时间复杂度大于 O(n!)，小于 O(n∗n!)，虽然没法知道非常精确的时间复杂度，但通过这个范围也能知道，全排列的时间复杂度是非常高的。