桶排序、计数排序、基数排序这些排序算法的时间复杂度都是 O(n) ，是线性的，所以这类排序算法也叫作线性排序（Linear sort）。原因是这三种算法都不是基于比较的排序算法，都不涉及元素之间的比较操作。都是典型的拿空间换时间的排序算法

桶排序（Bucket sort）

桶排序是计数排序的升级版，也采用了分治思想

原理

  • 将要排序的数据分到有限数量的几个有序的桶里。
  • 每个桶里的数据再单独进行排序（一般用插入排序或者快速排序）。
  • 桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

桶排序的核心：在于怎么把元素平均分配到每个桶里，合理的分配将大大提高排序的效率。在额外空间充足的情况下，尽量增大桶的数量。
image.png

代码实现

  1. 创建桶：二维数组数据结构“[ [ 5, 1 ], [ 10, 6, 7 ], [ 15 ], [ 19 ] ]”
    1. 要找出原始数组最大值与最小值
    2. 做一个桶的计算”((最大值-最小值)/默认分组桶的个数)+1”
  2. 把原始数组的元素分配到各个桶中
  3. 分别对各个桶做排序

  4. 合并排序后的桶，输出排序结果 ```javascript // 桶排序 const bucketSort = (array, bucketSize = 5) => { // bucketSize桶的大小，即桶存放数据的范围大小，注意不是存放的个数！！比如桶大小为5，最小值为5，那么第一个桶存放的数据范围是5~9，5~9范围数据的个数并不确定。 if (array.length <= 1) return array

    console.time(‘桶排序耗时’) // 第一步：找出原始数组最大值与最小值 const minValue = Math.min(…array) const maxValue = Math.max(…array)

    // 第二步：创建桶 const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1 // 算出桶的个数。一定要多一个桶，否则会漏掉最大值 const buckets = Array.from({ length: bucketCount }, () => []) // 将这些桶和数组进行规整成二维数组

    // 第三步：把原始数组的元素分配到各个桶中。注意，每个桶存的数量不一定相同，而且很有可能会超出桶的存储范围 for (i = 0; i < array.length; i++) { buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]) }

    // 第四步：分别对各个桶做排序 // 第五步：合并排序后的桶，输出排序结果 const sortedArray = [] for (let i = 0; i < buckets.length; i++) { if (buckets[i] != null) { // 此时桶已经是有序的，只要将桶里的数据进行排序即可，最后拼接在一起 sortedArray.push(…(buckets[i]).sort()) } } // 快速排序 // for (i = 0; i < buckets.length; i++) { // quickSort(buckets[i]) // 对每个桶进行排序，也可以使用快排 // for (var j = 0; j < buckets[i].length; j++) { // sortedArray.push(buckets[i][j]) // } // } console.timeEnd(‘桶排序耗时’) return sortedArray }

// 测试 console.log(‘newArr:’, bucketSort([22, 5, 11, 41, 45, 26, 29, 10, 7, 8, 30, 27, 44, 41, 42, 43, 40]))

  1. <a name="fXJak"></a>
  2. ## 复杂度分析
  3. 时间复杂度分析：<br />如果要排序的数据有 n 个，把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的**时间复杂度接近** **O(n)**。<br />**实际上，桶排序对要排序数据的要求是非常苛刻的：**
  5. 1. 要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
  6. 1. 数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。
  7. <a name="xC8sy"></a>
  8. ## 应用场景
  9. **适用场景：桶排序比较适合用在外部排序中**。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。<br />**举例：**比如有 10GB 的订单数据，希望按订单金额（假设金额都是正整数）进行排序，但是内存有限，只有几百 MB，没办法一次性把 10GB 的数据都加载到内存中。该怎么办？<br />先扫描一遍文件，看订单金额所处的数据范围。假设经过扫描之后得到，订单金额最小是 1 元，最大是 10 万元。再将所有订单根据金额划分到 100 个桶里，第一个桶存储金额在 1 元到 1000 元之内的订单，第二桶存储金额在 1001 元到 2000 元之内的订单，以此类推。每一个桶对应一个文件，并且按照金额范围的大小顺序编号命名（00，01，02…99）。<br />理想的情况下，如果订单金额在 1 到 10 万之间均匀分布，那订单会被均匀划分到 100 个桶中，每个桶中的存储大约 100MB 的订单数据，就可以将这 100 个桶装文件依次放到内存中，用快排来排序。等所有文件都排好序之后，只需要按照文件编号，从小到大依次读取每个小文件中的订单数据，并将其写入到一个文件中，那这个文件中存储的就是按照金额从小到大排序的订单数据了。<br />不过，有可能某个金额区间的数据特别多，划分之后对应的桶就会很大，没法一次性读入内存。这又该怎么办呢？针对这些划分之后还是比较大的文件，可以继续划分，比如，订单金额在 1 元到 1000 元之间的比较多，就将这个区间继续划分为 10 个小区间，1 元到 100 元，101 元到 200 元，201 元到 300 元…901 元到 1000 元。如果划分之后，101 元到 200 元之间的订单还是太多，无法一次性读入内存，那就继续再划分，直到所有的文件都能读入内存为止。
  10. <a name="krdxD"></a>
  11. # 计数排序（Counting sort）
  12. 每个桶里存放的数据都是一样大的，计数排序只能用在数据范围不大的场景中**，**并且计数排序只能针对**正整数**<br />![](https://www.yuque.com/api/filetransfer/images?url=https%3A%2F%2Fmmbiz.qpic.cn%2Fmmbiz_gif%2FbwG40XYiaOKkG2UVJzibXf4dzQ6N3DngUCOVjbOZA6F1XwWkamFJFDxTLNBR1fFIMA8Iz6JF2Cic8NjSVhCrMgmdQ%2F640%3Fwx_fmt%3Dgif&sign=a9124a1f0a2ca5651c604ab37fb123f6248dd8a94d1a83ff7866a96650476b7f#crop=0&crop=0&crop=1&crop=1&from=url&id=sPvXa&margin=%5Bobject%20Object%5D&originHeight=557&originWidth=1012&originalType=binary&ratio=1&rotation=0&showTitle=false&status=done&style=none&title=)
  13. <a name="KvEXD"></a>
  14. ## 原理
  15. 统计数组中每个元素出现的次数，存入新数组中。<br />关键要理解新数组的结构：新数组的索引代表原数组中的值，新数组的值代表原数组每个元素出现的次数<br />也就是说，新数组的索引就是已经是排好序的数组，只需要再根据值依次取出来展开就可以<br />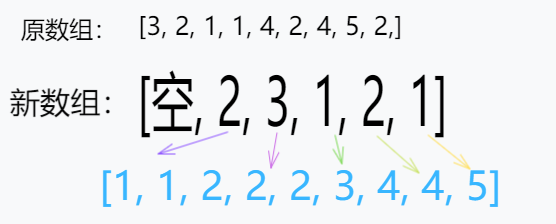![image.png](https://cdn.nlark.com/yuque/0/2022/png/915768/1653473932218-fb417162-9d14-434f-9e24-0c703621d1bd.png#clientId=u4ba31825-5aeb-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=224&id=u2c9e22ef&margin=%5Bobject%20Object%5D&name=image.png&originHeight=224&originWidth=556&originalType=binary&ratio=1&rotation=0&showTitle=false&size=29051&status=done&style=none&taskId=ua981b923-5b22-4168-bc23-adfdde4dfe4&title=&width=556)
  16. <a name="sGeWp"></a>
  17. ## 代码实现
  18. ```javascript
  19. function countingSort(array) {
  20.   if (array.length <= 1) {
  21.     return array
  22.   }
  24.   const counts = [] // ⭐索引index才是存储的数据值，值value存储的是这个数据出现几次
  25.   for (let i = 0; i < array.length; i++) { // 统计原数组每个值出现的次数，存在出现一次就 +1
  26.     // counts长度 = maxValue + 1
  27.     counts[array[i]] = counts[array[i]] ? counts[array[i]] + 1 : 1
  28.   }
  29.   // 此时counts的索引就是已经是排好序的数组，只需要再根据值依次取出来展开就可以
  30.   // 比如[空, 2, 3, 1, 2, 1]
  31.   // 那么依次取出展开就是2个1, 3个2, 1个3, 2个4, 1个5：[1, 1, 2, 2, 2, 3, 4, 4, 5]
  32.   console.log("🚀 ~ counts", counts)
  33.   let sortedIndex = 0
  34.   counts.forEach((count, index) => { // count代表这个数据出现几次，index代表这个数据的值
  35.     while (count > 0) { // 如果出现过，根据出现的次数依次展开
  36.       array[sortedIndex++] = index // sortedIndex作用就是重新排序
  37.       count--
  38.     }
  39.   })
  40.   return array
  41. }
  43. console.log(countingSort([3, 2, 1, 1, 4, 2, 4, 5, 2]))

基数排序（Radix sort）

原理

  • 基数排序是非比较型整数排序算法
  • 它将整数按位数切割成不同的数字，然后按照每个位数分别比较

桶、计数、基数 - 图2

代码实现

  1. 先将数组中的数据以个位为基数，进行第一次遍历排序，然后排序输出
  2. 再以未排序的十位数为基数，继续第二次遍历排序，然后排序输出
  3. 依次类推。总结而言：就是以数值的不同位为基数进行排序，所以叫基数排序
    1. const radixSort = (array, max) => { // max就是多少位。本例是手动传，也可以通过计算数组中最大值的位数
    2. console.time('基数排序耗时')
    3. const buckets = [] // 每轮每个桶存的的都是位数相同的数据
    4. let unit = 10,
    5.  base = 1
    6. for (let i = 0; i < max; i++, base *= 10, unit *= 10) {
    7.  for (let j = 0; j < array.length; j++) {
    8.    let index = ~~((array[j] % unit) / base) // 第一轮过滤出个位，第二轮十位...(~~有向下取整特性)
    9.    if (buckets[index] == null) {
    10.      buckets[index] = [] //初始化桶
    11.    }
    12.    buckets[index].push(array[j]) //往不同桶里添加数据
    13.  }
    14.  let pos = 0, // pos的作用是重头开始重新排序
    15.    value
    16.  for (let j = 0, length = buckets.length; j < length; j++) { // 遍历所有的桶，将桶里的数据依次取出
    17.    if (buckets[j] != null) {
    18.      while ((value = buckets[j].shift()) != null) { // 遍历第一个桶，将桶里的数据依次取出，然后继续第二个桶...
    19.        array[pos++] = value
    20.      }
    21.    }
    22.  }
    23.  // 第一轮过滤出来的数据先排好序，然后再下一轮
    24. }
    25. console.timeEnd('基数排序耗时')
    26. return arra
    27. }
    28. const newArr = radixSort([3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48], 2)
    29. console.log('newArr:', newArr)

    复杂度分析

  • 时间复杂度：基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要 O(n) 的时间复杂度，而且分配之后得到新的关键字序列又需要 O(n) 的时间复杂度。假如待排数据可以分为 d 个关键字，则基数排序的时间复杂度将是 O(d*2n) ，当然 d 要远远小于 n，因此基本上还是线性级别的
  • 空间复杂度：O(n)