原理

二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

代码实现

三个注意点：

  1. 循环退出条件：是 low<=high，而不是 low<high。
  2. mid 的取值：(low+high)/2 这种写法是有问题的，因为如果 low 和 high 比较大的话，两者之和就有可能会溢出。更进一步，如果要将性能优化到极致的话，可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说，计算机处理位运算要快得多。

3.low 和 high 的更新：low=mid+1，high=mid-1。如果直接写成 low=mid 或者 high=mid，就可能会发生死循环。

  1. const bsearch = (nums, target) => {
  2.   let low = 0,
  3.     high = nums.length - 1 //  下标
  4.   while (low <= high) { // 1.循环退出条件
  5.     const mid = Math.floor((high - low) / 2) + low // 2.求中间值
  6.     const num = nums[mid]
  7.     if (num === target) {
  8.       return mid
  9.     } else if (num > target) { // 3. 更新high
  10.       high = mid - 1
  11.     } else {
  12.       low = mid + 1
  13.     }
  14.   }
  15.   return -1
  16. }
  18. console.log("结果索引", bsearch([1, 2, 3, 4, 5, 6, 7], 5))

复杂度

时间复杂度： O(logn)。
O(logn) 这种对数时间复杂度是一种极其高效的时间复杂度，有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。因为即便 n 非常非常大，对应的 logn 也很小，比如n为232（42亿），用二分查找最多只需要32次！而O(1) 常量级时间复杂度，可能表示的是一个非常大的常量值，比如 O(1000)、O(10000)。所以，常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。

局限性

  1. 二分查找依赖的是顺序表结构，简单说就是数组。链表不行。
  2. 二分查找针对的是有序数据。如果数据没有序，需要先排序。
  3. 数据量太小不适合二分查找。如果数据量很小，完全没有必要用二分查找，顺序遍历就足够了。
  4. 数据量太大也不适合二分查找。二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，即使内存空间足够但是零散的不连续也不行！

    二分查找变体

    查找第一个值等于给定值的元素

    如果有重复的元素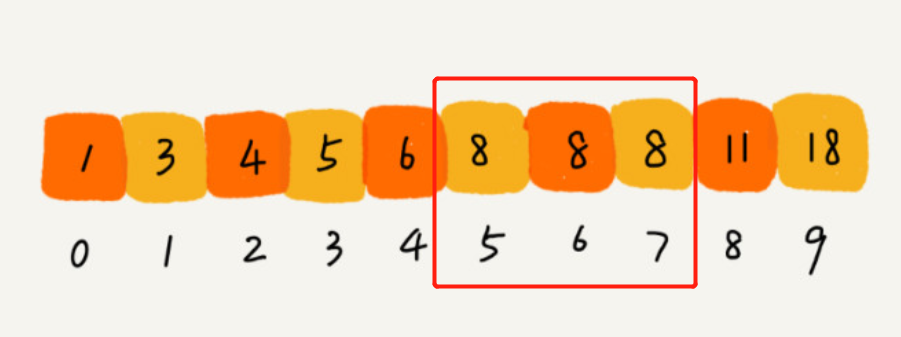image.png
    一般第一个都在左半边查找 ```javascript const bsearch = (nums, target) => { let low = 0, high = nums.length - 1 while (low <= high) { const mid = Math.floor((high - low) / 2) + low const num = nums[mid] if (num > target) { // 大于 high = mid - 1 } else if (num < target) { // 小于 low = mid + 1 } else { // 等于 // 1、如果mid等于0，那就说明是第一个元素，直接返回 // 2、如果mid不为0，并且mid前一个元素也等于target，那说明mid就是要找的第一个值，直接返回 if ((mid == 0) || (nums[mid - 1] != target)) return mid; // 3、否则，前面一个值也等于value，要找的元素肯定出现在[low, mid - 1]，那就更新high值，继续循环 else high = mid - 1 } } return -1 }

console.log(“结果索引”, bsearch([1, 3, 4, 5, 6, 8, 8, 8, 11, 18], 8)) // 结果索引 5

  1. <a name="ov36V"></a>
  2. ## 查找最后一个值等于给定值的元素
  3. 一般最后一个都在右半边查找
  4. ```javascript
  5. const bsearch = (nums, target) => {
  6.   let low = 0,
  7.       high = nums.length - 1
  8.   while (low <= high) {
  9.     const mid = Math.floor((high - low) / 2) + low
  10.     const num = nums[mid]
  11.     if (num > target) { // 大于
  12.       high = mid - 1
  13.     } else if (num < target) { // 小于
  14.       low = mid + 1
  15.     } else { // 等于
  16.       // 1、如果mid为最后一个元素，直接返回
  17.       // 2、如果mid不是最后一个元素，但是mid后一个元素不等于target，那说明mid就是要找的最后一个值
  18.       if ((mid == high) || (nums[mid + 1] != target)) return mid;
  19.       // 3、否则，后面一个值也等于value，要找的元素肯定出现在 [mid+1, high]，那就更新low值，继续循环
  20.       else low = mid + 1
  21.     }
  22.   }
  23.   return -1
  24. }
  26. console.log("结果索引", bsearch([1, 3, 4, 5, 6, 8, 8, 8, 11, 18], 8)) // 结果索引 7

查找第一个大于等于给定值的元素

一般第一个都在左半边查找

const bsearch = (nums, target) => {
  let low = 0,
    high = nums.length - 1
  while (low <= high) {
    const mid = Math.floor((high - low) / 2) + low
    const num = nums[mid]
    if (num >= target) { // 大于等于
      // 1、如果mid == 0，说明是第一个元素，肯定就是第一个值大于要查找的值，直接返回
      // 2、或者，前面一个元素小于要查找的值，那mid是要找的元素
      if ((mid == 0) || (nums[mid - 1] < target)) return mid
      // 3、否则，mid-1也大于要找的值，那就说明要找的元素在[low, mid-1] 之间，所以更新high
      else high = mid - 1
    } else {
      low = mid + 1
    }
  }
  return -1
}

console.log("结果索引", bsearch([3, 4, 6, 7, 10], 5)) // 结果索引 2

查找最后一个小于等于给定值的元素

一般最后一个都在右半边查找

const bsearch = (nums, target) => {
  let low = 0,
    high = nums.length - 1
  while (low <= high) {
    const mid = Math.floor((high - low) / 2) + low
    const num = nums[mid]
    if (num > target) {
      high = mid - 1
    } else { // 小于等于
      // 1、最后一个，直接返回
      // 2、查找到的后一个比给定值要大，那么也直接返回
      if ((mid == high) || (nums[mid + 1] > target)) return mid
      // 否则要找的值在右半边
      else low = mid + 1
    }
  }
  return -1
}

console.log("结果索引", bsearch([3, 4, 5, 6, 8, 9, 10], 7)) // 结果索引 3