一、第一期

1.反转二叉树(226)

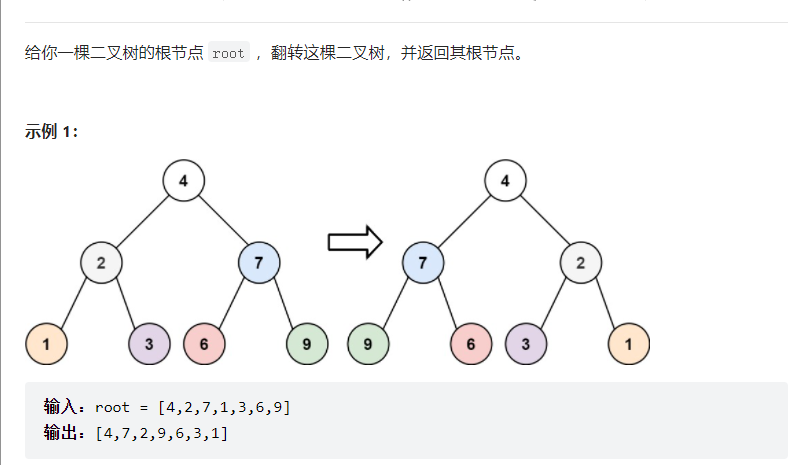
class Solution {
    // 将整棵树的节点翻转
    public TreeNode invertTree(TreeNode root) {
        // base case
        if (root == null) {
            return null;
        }
        /****前序遍历位置****/
        // 对于 root 节点，需要交换它的左右子节点
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        // 递归框架，遍历并交换子树所有节点
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

2.填充每个节点下的右侧节点指针(116)

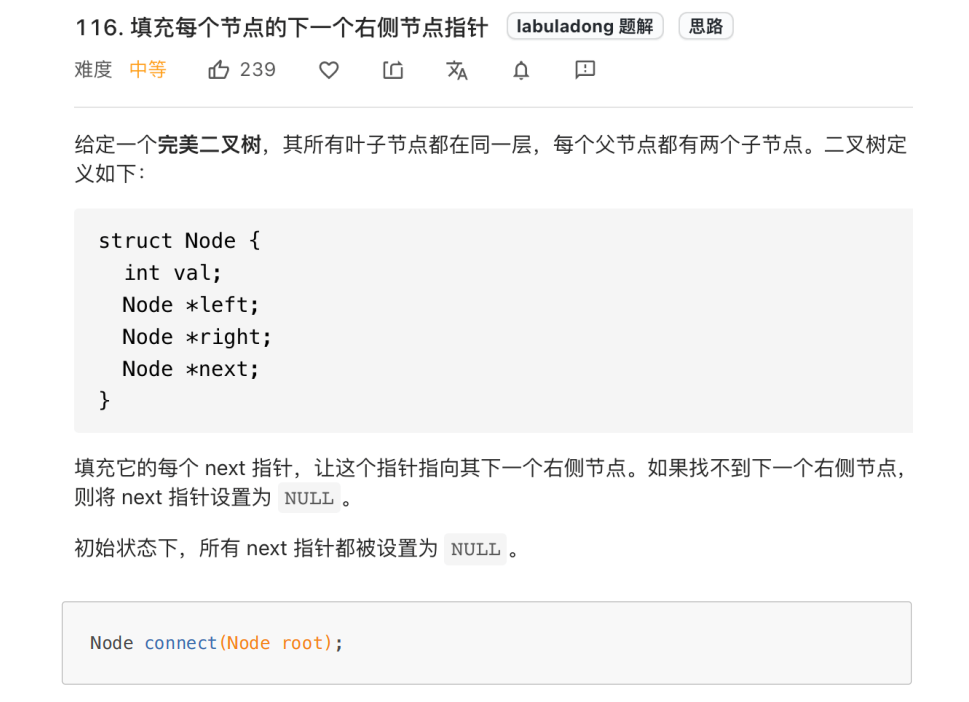
⽽且题⽬说了，输⼊是⼀棵「完美⼆叉树」，形象地说整棵⼆叉树是⼀个正三⻆形，除了最右侧的节点 next
指针会指向 null，其他节点的右侧⼀定有相邻的节点。
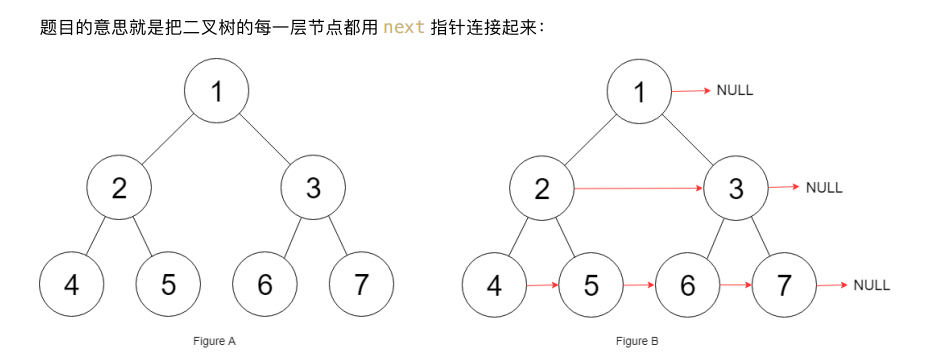
这道题怎么做呢？把每⼀层的节点穿起来，是不是只要把每个节点的左右⼦节点都穿起来就⾏了？
我们可以模仿上⼀道题，写出如下代码：

Node connect(Node root) {
 if (root == null || root.left == null) {
 return root;
 }
 root.left.next = root.right;
 connect(root.left);
 connect(root.right);
 return root;
}

节点 5 和节点 6 不属于同⼀个⽗节点，那么按照这段代码的逻辑，它俩就没办法被穿起来，这是不符合题意的

class Solution {
    public Node connect(Node root) {
        if (root == null) return null;
        connectTwoNode(root.left, root.right);
        return root;
    }
    // 辅助函数
    void connectTwoNode(Node node1, Node node2) {
        if (node1 == null || node2 == null) {
            return;
        }
        /****前序遍历位置****/
        // 将传入的两个节点连接
        node1.next = node2;
        // 连接相同父节点的两个子节点
        connectTwoNode(node1.left, node1.right);
        connectTwoNode(node2.left, node2.right);
        // 连接跨越父节点的两个子节点
        connectTwoNode(node1.right, node2.left);
    }
}

3.二叉树展开为链表(114)

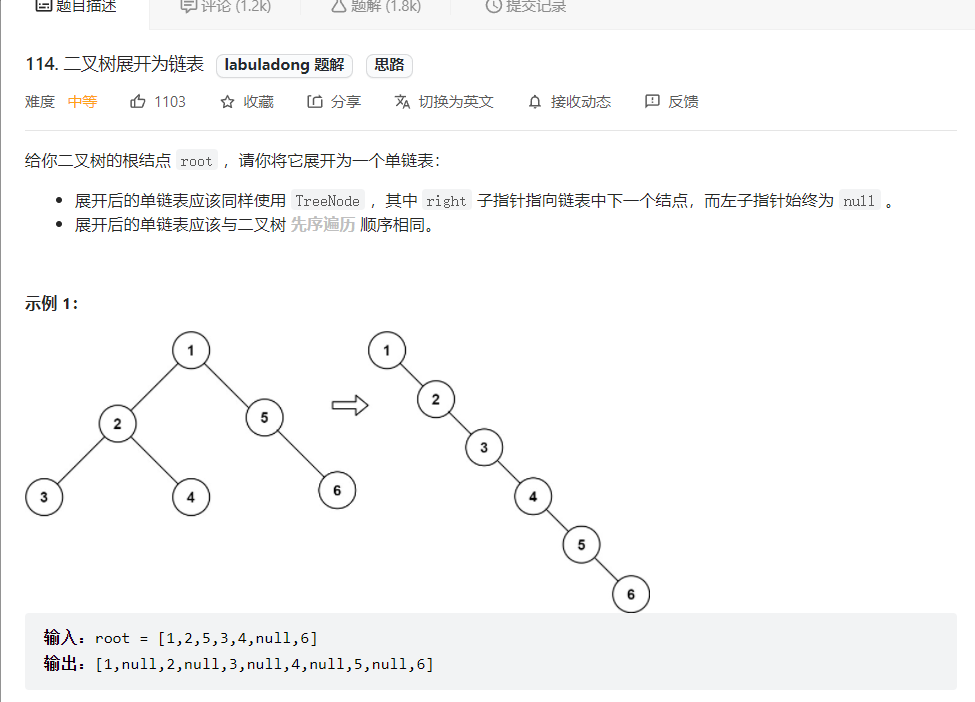
前文手把手刷二叉树总结篇说过二叉树的递归算法可以分两类，一类是遍历二叉树的类型，一类是分解子问题的类型。
前者较简单，只要运用二叉树的递归遍历框架即可；后者的关键在于明确递归函数的定义，然后利用这个定义。
这题属于后者，flatten 函数的定义：
给 flatten 函数输入一个节点 root，那么以 root 为根的二叉树就会被拉平为一条链表。
如何利用这个定义来完成算法？你想想怎么把以 root 为根的二叉树拉平为一条链表？
很简单，以下流程：
1、将 root 的左子树和右子树拉平。
2、将 root 的右子树接到左子树下方，然后将整个左子树作为右子树。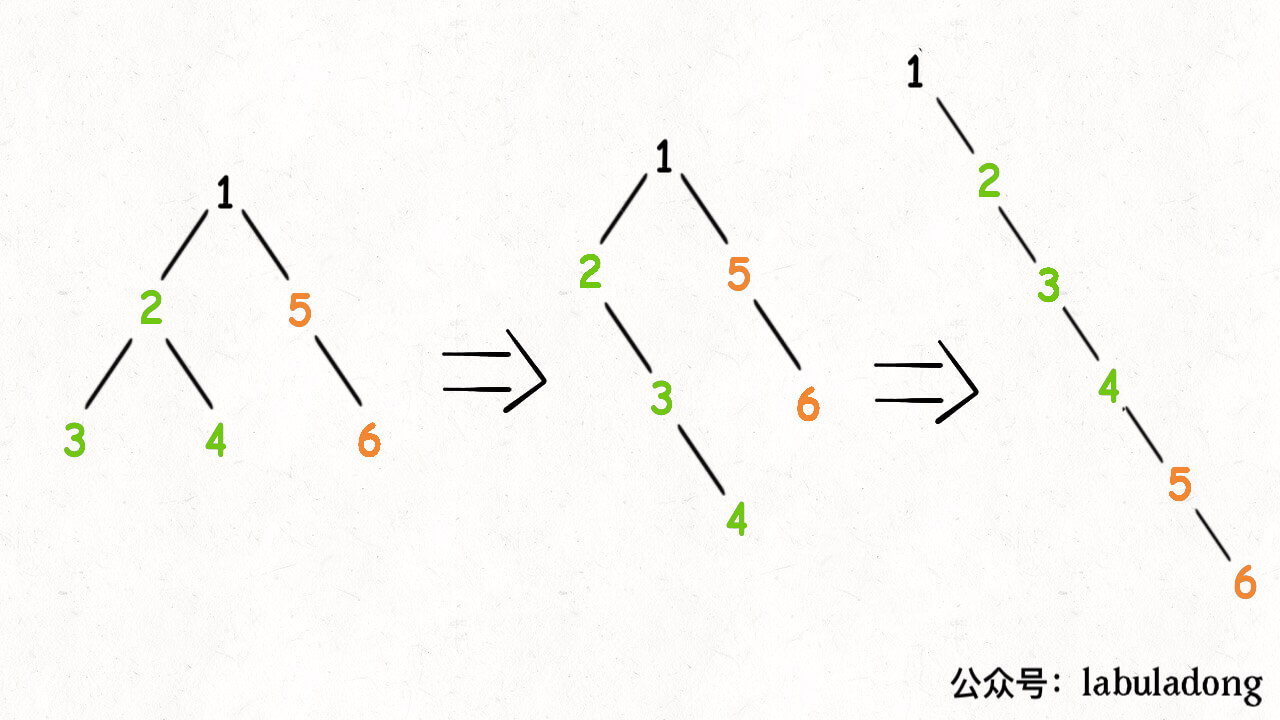
二、树 - 图5
注意:一定不要忘了把左子树置空root.left=null;

class Solution {
    // 定义：将以 root 为根的树拉平为链表
    public void flatten(TreeNode root) {
        // base case
        if (root == null) return;
        // 先递归拉平左右子树
        flatten(root.left);
        flatten(root.right);
        /****后序遍历位置****/
        // 1、左右子树已经被拉平成一条链表
        TreeNode left = root.left;
        TreeNode right = root.right;
        // 2、将左子树作为右子树
        root.left = null;
        root.right = left;
        // 3、将原先的右子树接到当前右子树的末端
        TreeNode p = root;
        while (p.right != null) {
            p = p.right;
        }
        p.right = right;
    }
}

二、第二期

1.最大二叉树(654)

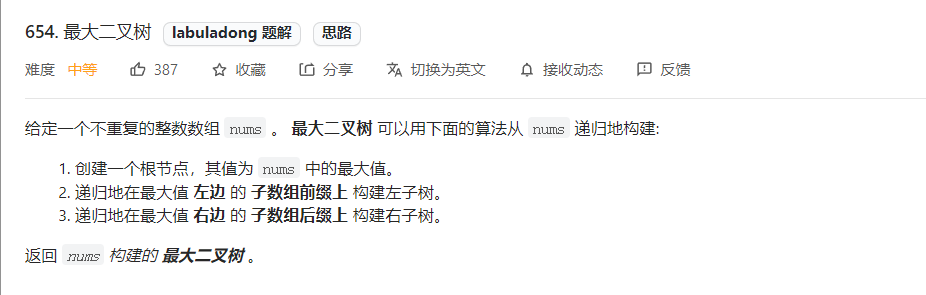
class Solution {
    /* 主函数 */
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }
    /* 定义：将 nums[lo..hi] 构造成符合条件的树，返回根节点 */
    TreeNode build(int[] nums, int lo, int hi) {
        // base case
        if (lo > hi) {
            return null;
        }
        // 找到数组中的最大值和对应的索引
        int index = -1, maxVal = Integer.MIN_VALUE;
        for (int i = lo; i <= hi; i++) {
            if (maxVal < nums[i]) {
                index = i;
                maxVal = nums[i];
            }
        }
        TreeNode root = new TreeNode(maxVal);
        // 递归调用构造左右子树
        root.left = build(nums, lo, index - 1);
        root.right = build(nums, index + 1, hi);
        return root;
    }
}

2.从前序与中序遍历序列构造二叉树(105)

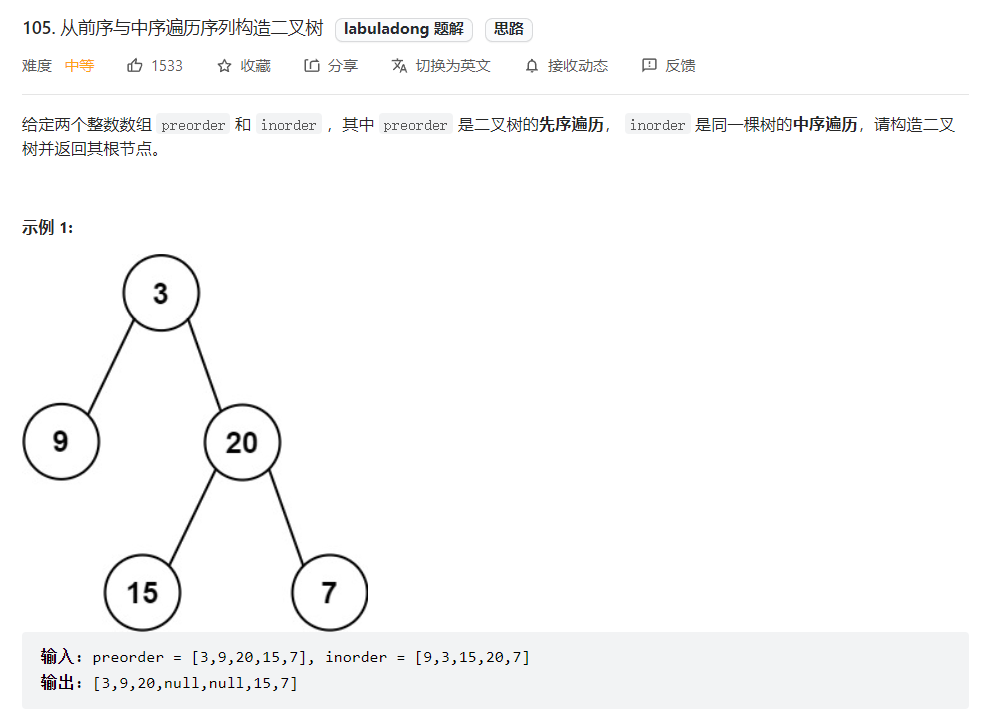
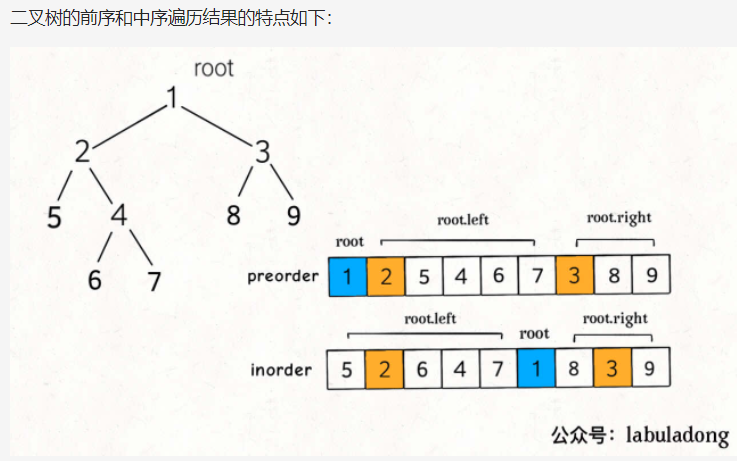
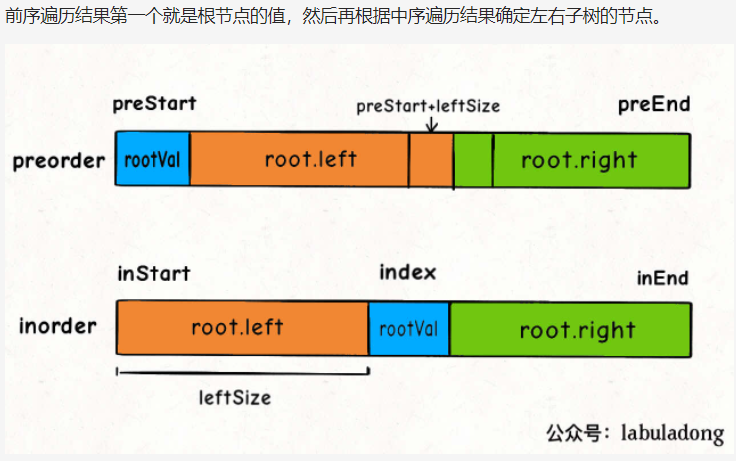
class Solution {
    // 存储 inorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1,
                     inorder, 0, inorder.length - 1);
    }
    /*
    定义：前序遍历数组为 preorder[preStart..preEnd]，
    中序遍历数组为 inorder[inStart..inEnd]，
    构造这个二叉树并返回该二叉树的根节点
    */
    TreeNode build(int[] preorder, int preStart, int preEnd,
                   int[] inorder, int inStart, int inEnd) {
        if (preStart > preEnd) {
            return null;
        }
        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // rootVal 在中序遍历数组中的索引
        int index = valToIndex.get(rootVal);
        int leftSize = index - inStart;
        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                          inorder, inStart, index - 1);
        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                           inorder, index + 1, inEnd);
        return root;
    }
}
// 详细解析参见：
// https://labuladong.gitee.io/article/?qno=105

3.从中序与后序遍历序列构造二叉树(106)

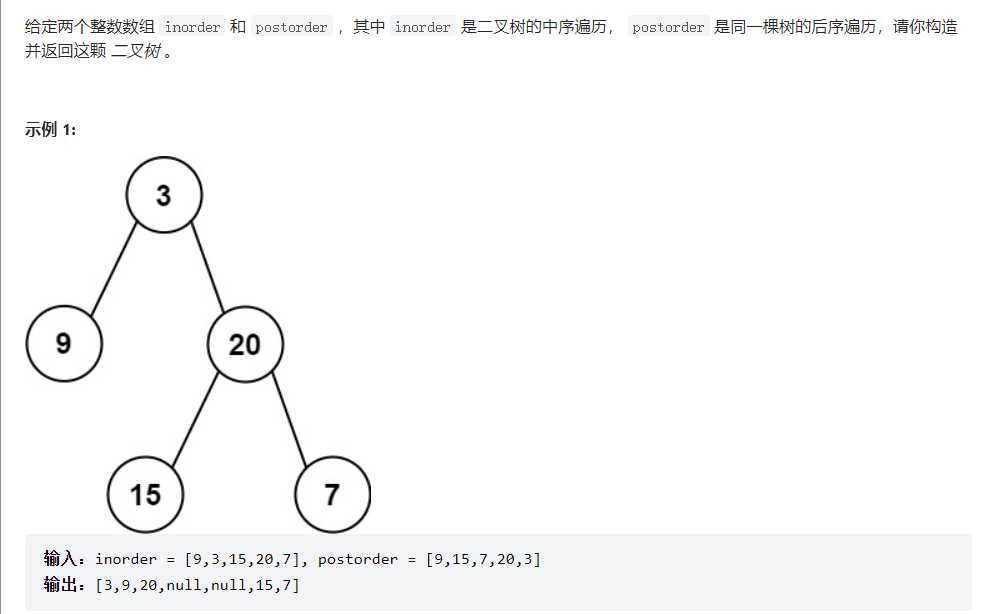
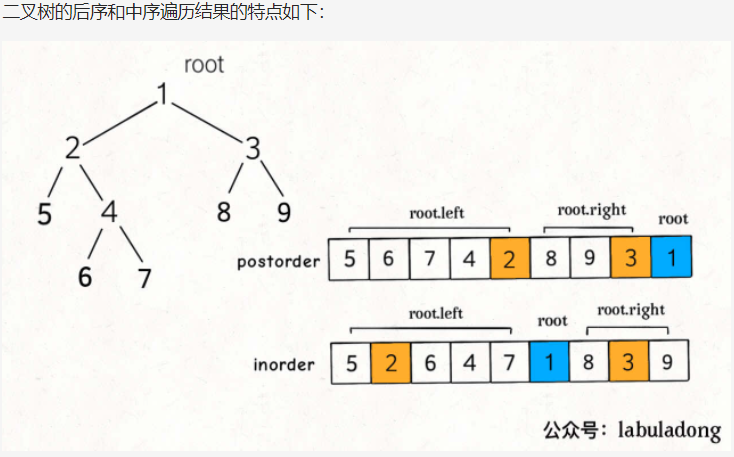
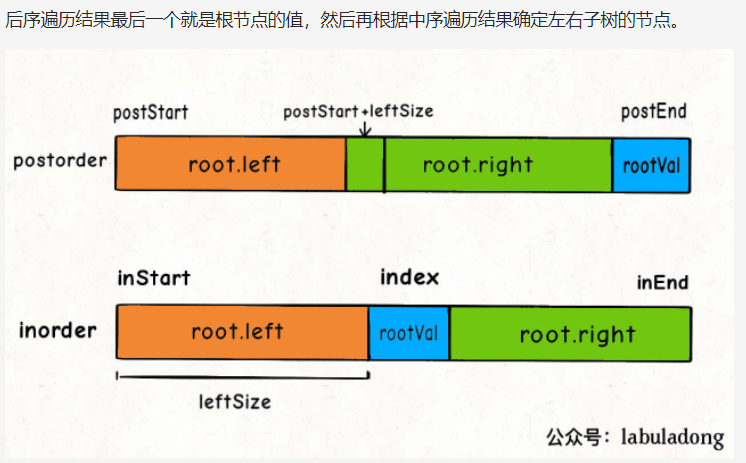
class Solution {
    // 存储 inorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; i++) {
            valToIndex.put(inorder[i], i);
        }
        return build(inorder, 0, inorder.length - 1,
                    postorder, 0, postorder.length - 1);
    }
    /*
       定义：
       中序遍历数组为 inorder[inStart..inEnd]，
       后序遍历数组为 postorder[postStart..postEnd]，
       构造这个二叉树并返回该二叉树的根节点
    */
    TreeNode build(int[] inorder, int inStart, int inEnd,
                int[] postorder, int postStart, int postEnd) {
        if (inStart > inEnd) {
            return null;
        }
        // root 节点对应的值就是后序遍历数组的最后一个元素
        int rootVal = postorder[postEnd];
        // rootVal 在中序遍历数组中的索引
        int index = valToIndex.get(rootVal);
        // 左子树的节点个数
        int leftSize = index - inStart;
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        root.left = build(inorder, inStart, index - 1,
                         postorder, postStart, postStart + leftSize - 1);
        root.right = build(inorder, index + 1, inEnd,
                          postorder, postStart + leftSize, postEnd - 1);
        return root;
    }
}

4. 通过后序和前序遍历结果构造⼆叉树 (889)

这道题和前两道题有⼀个本质的区别：
通过前序中序，或者后序中序遍历结果可以确定⼀棵原始⼆叉树，但是通过前序后序遍历结果⽆法确定原始⼆叉树。
题⽬也说了，如果有多种可能的还原结果，你可以返回任意⼀种。
为什么呢？我们说过，构建⼆叉树的套路很简单，先找到根节点，然后找到并递归构造左右⼦树即可。
前两道题，可以通过前序或者后序遍历结果找到根节点，然后根据中序遍历结果确定左右⼦树。
这道题，你可以确定根节点，但是⽆法确切的知道左右⼦树有哪些节点。
举个例⼦，下⾯这两棵树结构不同，但是它们的前序遍历和后序遍历结果是相同的：

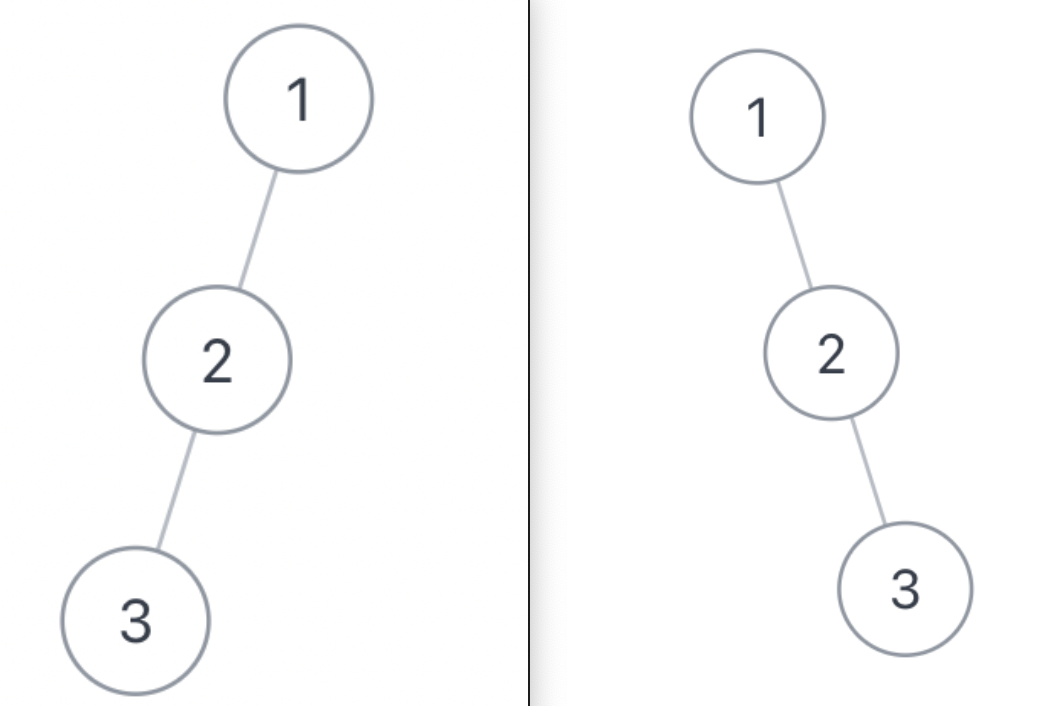
不过话说回来，⽤后序遍历和前序遍历结果还原⼆叉树，解法逻辑上和前两道题差别不⼤，也是通过控制左右⼦树的索引来构建：
1、⾸先把前序遍历结果的第⼀个元素或者后序遍历结果的最后⼀个元素确定为根节点的值。
2、然后把前序遍历结果的第⼆个元素作为左⼦树的根节点的值。
3、在后序遍历结果中寻找左⼦树根节点的值，从⽽确定了左⼦树的索引边界，进⽽确定右⼦树的索引边界，递归构造左右⼦树即可。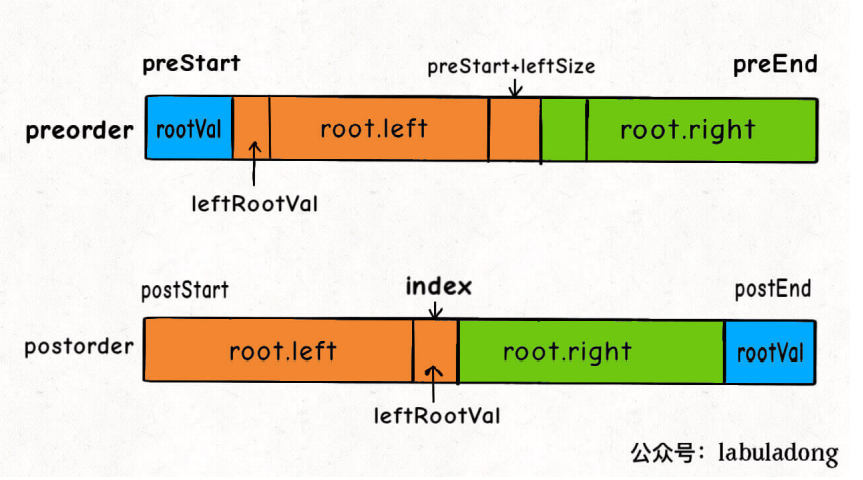

class Solution {
    // 存储 postorder 中值到索引的映射
    HashMap<Integer, Integer> valToIndex = new HashMap<>();
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        for (int i = 0; i < postorder.length; i++) {
            valToIndex.put(postorder[i], i);
        }
        return build(preorder, 0, preorder.length - 1,
                     postorder, 0, postorder.length - 1);
    }
    // 定义：根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
    // 构建二叉树，并返回根节点。
    TreeNode build(int[] preorder, int preStart, int preEnd,
                   int[] postorder, int postStart, int postEnd) {
        if (preStart > preEnd) {
            return null;
        }
        if (preStart == preEnd) {
            return new TreeNode(preorder[preStart]);
        }
        // root 节点对应的值就是前序遍历数组的第一个元素
        int rootVal = preorder[preStart];
        // root.left 的值是前序遍历第二个元素
        // 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
        // 确定 preorder 和 postorder 中左右子树的元素区间
        int leftRootVal = preorder[preStart + 1];
        // leftRootVal 在后序遍历数组中的索引
        int index = valToIndex.get(leftRootVal);
        // 左子树的元素个数
        int leftSize = index - postStart + 1;
        // 先构造出当前根节点
        TreeNode root = new TreeNode(rootVal);
        // 递归构造左右子树
        // 根据左子树的根节点索引和元素个数推导左右子树的索引边界
        root.left = build(preorder, preStart + 1, preStart + leftSize,
                          postorder, postStart, index);
        root.right = build(preorder, preStart + leftSize + 1, preEnd,
                           postorder, index + 1, postEnd - 1);
        return root;
    }
}

代码和前两道题⾮常类似，我们可以看着代码思考⼀下，为什么通过前序遍历和后序遍历结果还原的⼆叉树可能不唯⼀呢？关键在这⼀句：

int leftRootVal = preorder[preStart + 1];

我们假设前序遍历的第⼆个元素是左⼦树的根节点，但实际上左⼦树可能是空指针，这个元素可能是右⼦树的根节点。由于这⾥⽆法确切进⾏判断，所以导致了最终答案的不唯⼀。⾄此，通过前序和后序遍历结果还原⼆叉树的问题也解决了。

三、第三期

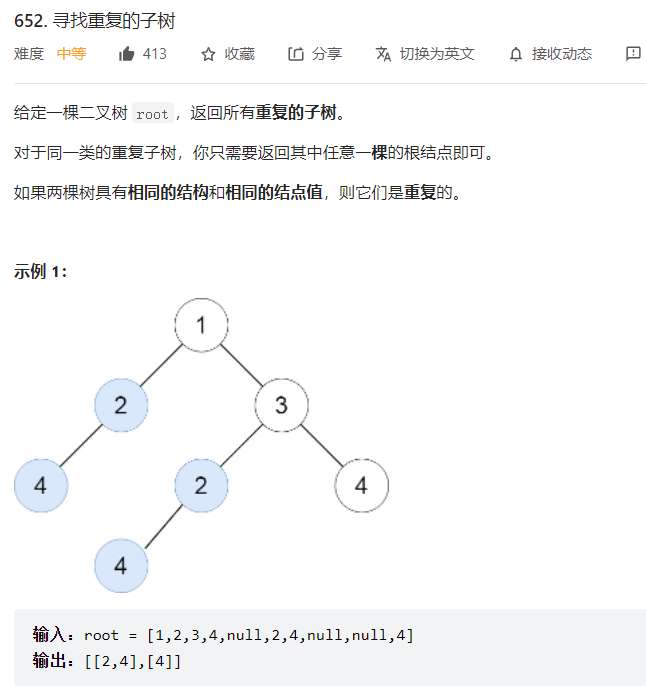
1.寻找重复的子树(652)

基本思路

比如说，你站在图中这个节点 2 上：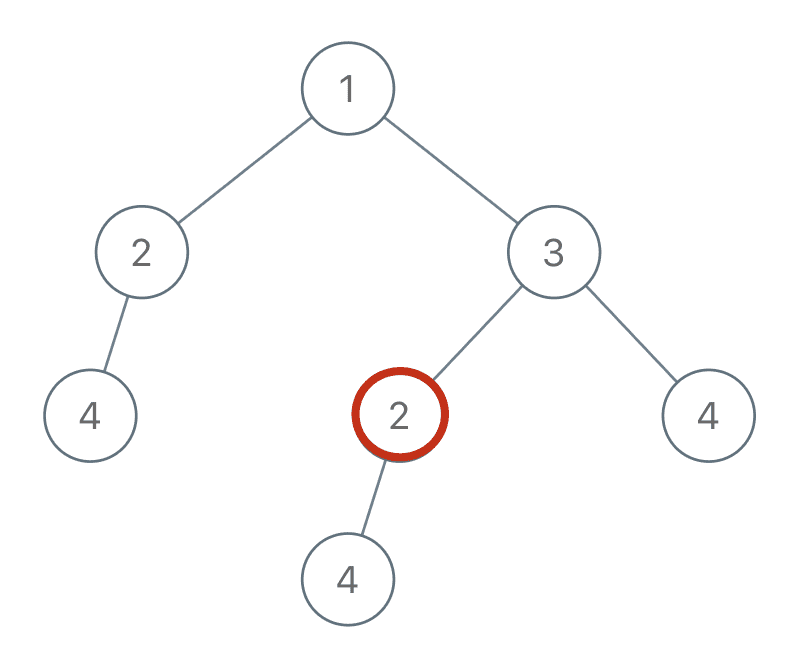

如果你想知道以自己为根的子树是不是重复的，是否应该被加入结果列表中，你需要知道什么信息？
你需要知道以下两点：
1、以我为根的这棵二叉树（子树）长啥样？
2、以其他节点为根的子树都长啥样？
这就叫知己知彼嘛，我得知道自己长啥样，还得知道别人长啥样，然后才能知道有没有人跟我重复，对不对？
我怎么知道自己以我为根的二叉树长啥样？前文序列化和反序列化二叉树其实写过了，二叉树的前序/中序/后序遍历结果可以描述二叉树的结构。
我咋知道其他子树长啥样？每个节点都把以自己为根的子树的样子存到一个外部的数据结构里即可。
按照这个思路看代码就不难理解了。

class Solution {
    // 记录所有子树以及出现的次数
    HashMap<String, Integer> memo = new HashMap<>();
    // 记录重复的子树根节点
    LinkedList<TreeNode> res = new LinkedList<>();
    /* 主函数 */
    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        traverse(root);
        return res;
    }
    String traverse(TreeNode root) {
        if (root == null) {
            return "#";
        }
        String left = traverse(root.left);
        String right = traverse(root.right);
        String subTree = left + "," + right + "," + root.val;
        int freq = memo.getOrDefault(subTree, 0);
        // 多次重复也只会被加入结果集一次
        if (freq == 1) {
            res.add(root);
        }
        // 给子树对应的出现次数加一
        memo.put(subTree, freq + 1);
        return subTree;
    }
}