概念

基数(cardinality，也译作势)，是指一个集合中不重复元素的个数。这里的集合和我们学过的严格定义的集合不同，允许存在重复元素，被称作multi-set，如给定这样的一个集合{1,2,3,1,2}，它有5个元素, 基数是3

基数计数(cardinality counting)，则是指计算一个集合的基数，意即count-discint。 基数计算的场景很广泛，例如计算网站的访问uv，计算网络流量网络包请求header中的源地址的distinct数来作为网络攻击的重要指标。想要实现基数计数最直接想到的方式就是通过字典/HashSet，每条数据流入后直接保存相应的key，最后统一次集合的size就得到集合的基数。但是，这种方法的空间复杂度很高，在面对大数据的场景下做这样的统计代价很高。在近几十年有学者提出了很多基数估算的算法，在容许一定的误差的情况下，基于统计概率进行估算，本文就来介绍其中比较有名的几个基数估计算法

基数估计算法

Linear Counting

Linear Counting（以下简称LC）在1990年的一篇论文“A linear-time probabilistic counting algorithm for database applications”中被提出。作为一个早期的基数估计算法，LC在空间复杂度方面并不算优秀，是, 因此目前很少单独使用LC。

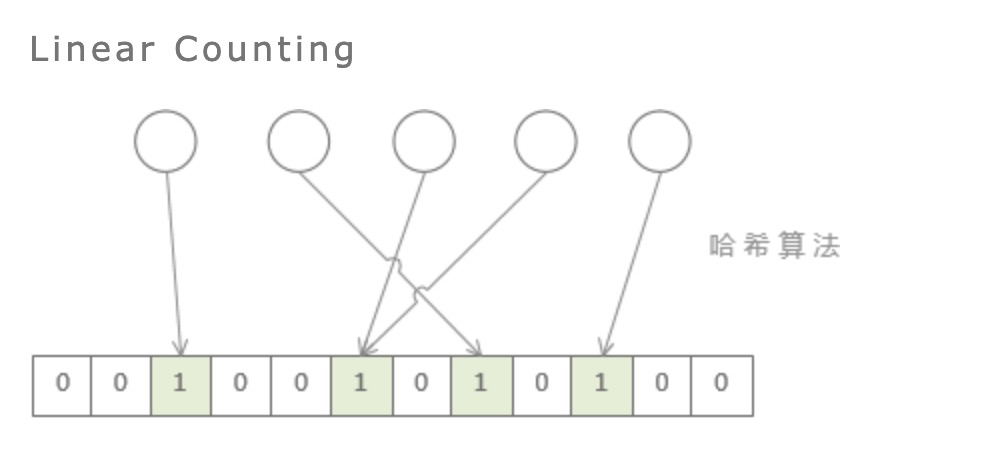
LC的基本思路是：设有一哈希函数H，其哈希结果空间有m个值（最小值0，最大值m-1），并且哈希结果服从均匀分布。使用一个长度为m的bitmap，每个bit为一个桶，均初始化为0，设一个集合的基数为n，此集合所有元素通过H哈希到bitmap中，如果某一个元素被哈希到第k个比特并且第k个比特为0，则将其置为1。当集合所有元素哈希完成后，设bitmap中还有u个bit为0。则：, 这里证明过程就略过了，包含比较多的概率论相关的知识点。

下图是论文作者预先计算出的关于不同基数量级和误差情况下，m的选择表：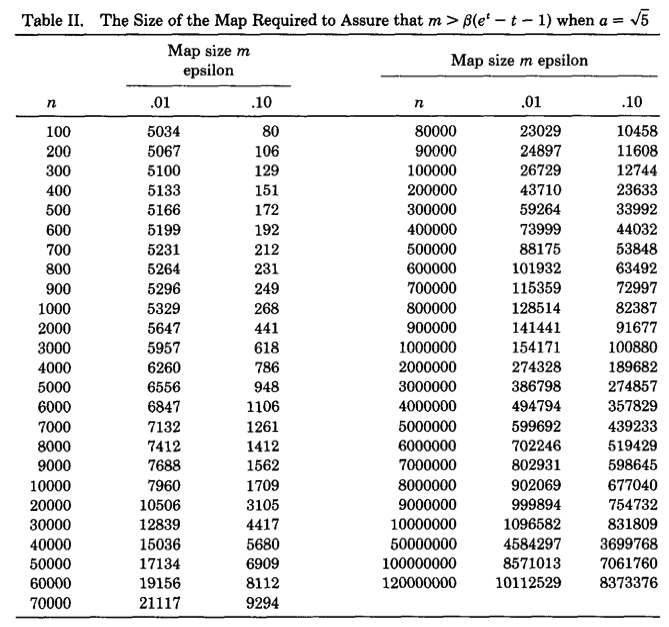

可以看出精度要求越高，则bitmap的长度越大。随着m和n的增大，m大约为n的十分之一。因此LC所需要的空间只有传统的bitmap直接映射方法的1/10，但是从渐进复杂性的角度看，空间复杂度仍为但是他在元素较少的时候表现是比较好的，也因为作为其他几个算法的误差修正的手段

LogLog Counting

LogLog Counting（以下简称LLC）出自论文“Loglog Counting of Large Cardinalities”。LLC的空间复杂度仅有，使得通过KB级内存估计数亿级别的基数成为可能，因此目前在处理大数据的基数计算问题时，所采用算法基本为LLC或其几个变种

算法思想
LLC算法也假设有一个Hash函数，能将原始的数据映射成一个基本服从均匀分布的结果，这里忽略到Hash碰撞的情况。这样在hash之后，我们就能得到一个比特串 a，a的长度是L，因为hash结果是服从均匀分布的，所以每一位为0或者1的概率都为1/2，且相互独立。那么我们假设为a中第一个”1”出现的位置，。遍历集合中所有元素的比特串（每个元素都经过hash函数生成一个比特串）, 取为所有的最大值，这里将作为基数的粗糙估计， 即

这个算法的思想可以用抛硬币的实验来类比理解一下，在一个抛硬币的场景下，假设硬币的正面对应着1， 硬币的反面对应着0; 依次扔出0, 0, 0, 1的概率是多少？通过概率计算可以得到是这个概率是 那么相当于平均需要扔16次，才会获得 0001 这个序列。反之，如果出现了 0001 这个序列，说明起码抛了 16 次硬币。

那这样近似计算的理论依据是什么？

从比特串中（每个比特串独立且服从0-1分布），从左到右扫描比特串的第一个”1”的过程从统计学上叫伯努利过程。等价于

不断投掷一个硬币，直到得到一个正面的过程，在一次这样的过程中投掷一次就得到正面的概率为1/2，投掷两次得到正面的概率是1/4，…，投掷k次才得到第一个正面的概率为

现在考虑两个问题:

1. 抛n次硬币，所有投掷次数都不大于k的概率是多少 P1
2. 抛n次硬币，至少有一次投掷次数等于k的概率是多少 P2

问题一

• 所有投掷次数都不大于k的概率 = 一次过程中投掷次数不大于k的概率 =
• 一次过程中投掷次数不大于k的概率 = 1 - 一次过程中投掷次数大于k的概率 = 1 -
• 一次过程中投掷次数大于k的概率 = 连续掷出k个反面的概率 =

问题二

• 至少有一次投掷次数等于k的概率 = 1 - N次伯努利过程均不等于k的概率 =
• N次伯努利过程均不等于k的概率 = 一次过程中不等于k的概率 =
  
• 一次过程中不等于k的概率 = 1 - 投掷次数为k的概率 =
• 投掷次数等于k的概率 = 连续k-1次都是反面，是

从以上分析可以看出，当时，P2的概率几乎为0，同时，当时，P1的概率也几乎为0。
用自然语言概括上述结论就是：当伯努利过程次数远远小于时，至少有一次过程投掷次数等于k的概率几乎为0；当伯努利过程次数远远大于时，没有一次过程投掷次数大于k的概率也几乎为0。

如果将上面描述做一个对应：一次伯努利过程对应一个元素的比特串，反面对应0，正面对应1，投掷次数k对应第一个“1”出现的位置，我们就得到了下面结论：

设一个集合的基数为n，为所有元素中首个“1”的位置最大的那个元素的“1”的位置，如果n远远小于，则我们得到为当前值的概率几乎为0（它应该更小），同样的，如果n远远大于，则我们得到为当前值的概率也几乎为0（它应该更大），因此可以作为基数n的一个粗糙估计。

但是如果直接使用单一的估计量会由于偶然性而存在较大的误差，因此LLC采用了分桶平均的思想来消除误差。具体来说，就是降哈希空间平均分成m份，每份称之为一个桶，对于每个元素，其hash值的前K比特位作为桶的编号，其中,而后L-k比特作为真正用于基数估计的比特串，桶编号相同的元素被分配到同一个桶，在进行基数估计时，首先计算每个桶内元素最大的第一个”1”的位置，设为M[i]，然后对这m个值去平均再进行估计即:

这相当于物理试验中经常使用的多次试验取平均的做法，可以有效消减因偶然性带来的误差。
与LC算法相比LLC的空间复杂度下降了很多直接变成LogLog量级，这也是其算法名称的由来，但是LLC算法存在一个问题就是在n不是特别大的时候误差估计较大，主要原因是基数不大时，可能存在一些空桶，这些空桶的为0，由于LLC的估计值依赖各个桶的的几何平均数，而几何平均数对于0这种特殊值比较敏感，因此存在一些空桶时就会误差比较大。
目前生产使用的一些算法都是基于LLC的改进算法，这些改进算法通过一定手段抑制原始LLC在n较小时偏差过大的问题

HyperLogLog Counting 和 Adaptive Counting

这两个算法主要是在LLC算法上的改进，大体思想没有变
AC算法在Fast and accurate traffic matrix measurement using adaptive cardinality counting提出，思想比较直观，是直接将LC和LLC算法组合使用，根据数量级决定使用LC还是LLC。
HLL的改进是使用调和平均数替代几何平均数，调和平均数可以有效抵抗离群值的扰动，并且在实现部分作者还提供了再n相对于m较小或者较大时的偏差修正的方案

关于HLL算法有一个动态演示的网站可以看到每个输入元素的插入过程

1. 插入数据16751354
2. 计算出hashcode1247735109
3. 从后6位计算出插入的index为6，也就是会将插入第6个桶
4. 从剩余的位数从右往左数得到 = 1
5. 最后由所有的位桶计算得到基数估计值

Flajolet–Martin

Flajolet–Martin算法其实不应该放在这个位置说，因为LLC和HLL其实都是FM-sketch的衍生，不过是我再了解过程中最后才了解到，因此这里稍微补充下。在论文中两位作者给出了比较完整的和上文LLC中分析的基于伯努利过程的概率计算模型，也提出了改进的方案：PCSA-Probabilistic counting with stochastic averaging
其实就是上面LLC中提到的降bitmap分成m组，目的是为了增多实验数据，避免单一数据带来的偏差过大，有兴趣的话可以看下这篇文章:https://www.jianshu.com/p/4bddbcdd89df

实际上基数估计的算法还有很多，观察方式也还有很多，本文介绍的应该主要是基于Bit-pattern的LogLog派系的，其他的有机会再研究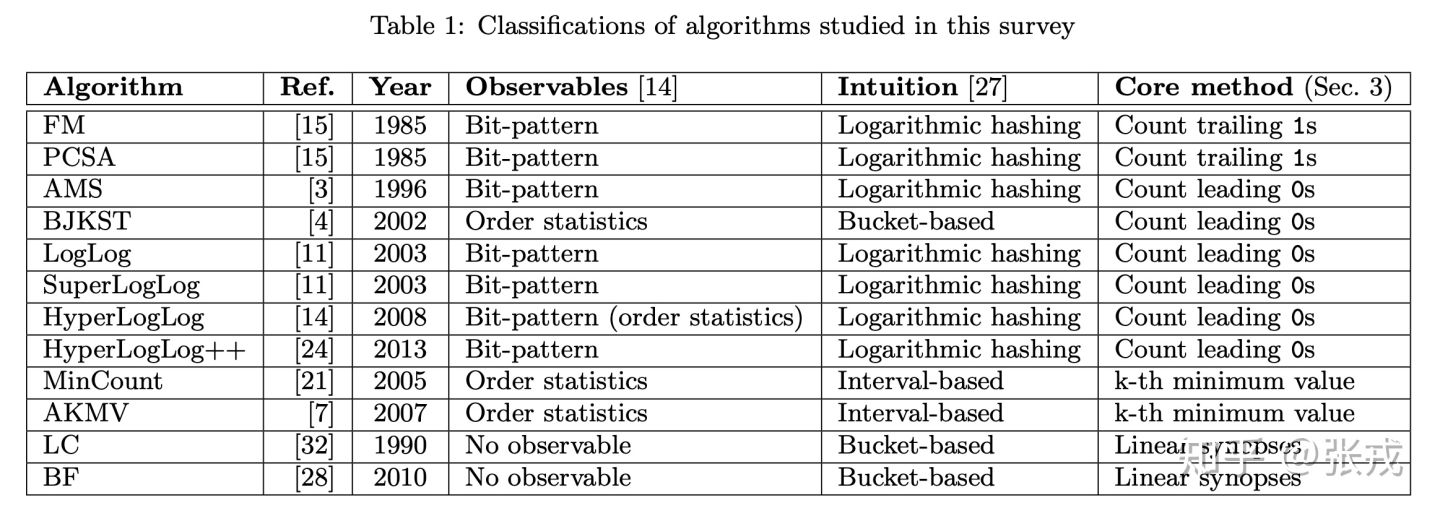

参考文章

• https://zhuanlan.zhihu.com/p/141344814 这篇文章以非常通俗易懂的方式介绍了Hll算法的原理
• http://www.yoonper.com/post.php?id=79
• https://www.jianshu.com/p/1327d03c8124
• http://blog.codinglabs.org/articles/algorithms-for-cardinality-estimation-part-i.html
• http://blog.codinglabs.org/articles/algorithms-for-cardinality-estimation-part-ii.html
• http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm
• http://algo.inria.fr/flajolet/Publications/FlMa85.pdf Flajolet–Martin 算法论文
• http://content.research.neustar.biz/blog/hll.html hll算法的可视化的测试网站
• https://bindog.github.io/blog/2015/02/14/cardinality-counting/ 如何科学的计数
• https://zhuanlan.zhihu.com/p/19930815 伪随机与真随机

几个算法实现的工程

• https://github.com/addthis/stream-lib/blob/master/src/main/java/com/clearspring/analytics/stream/cardinality/HyperLogLog.java
• https://github.com/apache/incubator-datasketches-java/tree/master/src/main/java/org/apache/datasketches/hll