42.接雨水 难

作者：Sweetiee姨
链接：https://zhuanlan.zhihu.com/p/125074613

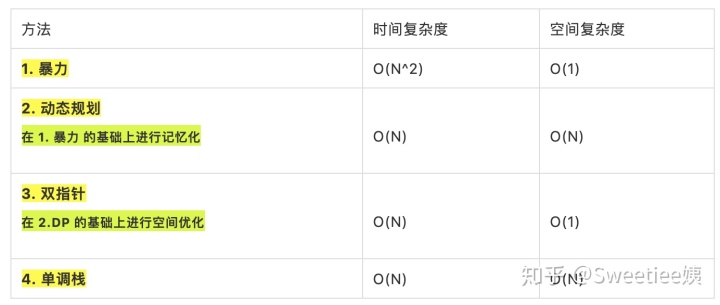
1、暴力 时间O(N^2) 空间O(1)

很明显每个柱子顶部可以储水的高度为：该柱子的左右两侧最大高度的较小者减去此柱子的高度。
因此我们只需要遍历每个柱子，累加每个柱子可以储水的高度即可。
此方法非常好理解，

//1，暴力法，时间N^2,空间1
func trap(height []int) int {
    n := len(height)    //长度，横坐标
    res := 0    //面积初值
    for i :=1; i <n-1; i++ {    //找中间点，作为参照点
        leftMax := 0
        for k := 0; k <= i; k++ {      //针对每一个中间点，找左边最大值
            leftMax = max(height[k],leftMax)    //为啥是k<=i，有=？
        }
        rightMax := 0
        for j := i; j < n ;j++ {    //针对每一个中间点，找右边最大值
            rightMax = max(height[j], rightMax)
        }
        minVal := min(leftMax,rightMax)     //核心，找到左右边界的较小值
        water := minVal - height[i]         //计算水量公式
        res = res + water
    }
    return res
}
func max(a,b int)int {
    if a>b {
        return a
    }
    return b
}
func min(a,b int)int {
    if a>b {
        return b
    }
    return a
}

2、动态规划 时间O(N) 空间O(N)

在上述的暴力法中，对于每个柱子，我们都需要从两头重新遍历一遍求出左右两侧的最大高度，这里是有很多重复计算的，很明显最大高度是可以记忆化的，具体在这里可以用数组边递推边存储，也就是常说的动态规划，DP。

预处理最值解法

朴素解法的思路有了，我们想想怎么优化。
事实上，任何的优化无非都是「减少重复」。
想想在朴素思路中有哪些环节比较耗时，耗时环节中又有哪些地方是重复的，可以优化的。
首先对每根柱子进行遍历，求解每根柱子可以接下多少雨水，这个 O(n)操作肯定省不了。
但在求解某根柱子可以接下多少雨水时，需要对两边进行扫描，求两侧的最大值。每一根柱子都进行这样的扫描操作，导致每个位置都被扫描了 n 次。这个过程显然是可优化的。
换句话说：我们希望通过不重复遍历的方式找到任意位置的两侧最大值。
问题转化为：给定一个数组，如何求得任意位置的左半边的最大值和右半边的最大值。
一个很直观的方案是：直接将某个位置的两侧最大值存起来。
我们可以先从两端分别出发，预处理每个位置的「左右最值」，这样可以将我们「查找左右最值」的复杂度降到 O(1)。
整体算法的复杂度也从 O(n^2) 下降到 O(n)。

//动态规划
func trap(height []int)int{
    if len(height)==0{
        return 0
    }
    size :=len(height)
    res :=0
    leftDP :=make([]int,size)
    rightDP :=make([]int,size)
    leftDP[0]= height[0]
    rightDP[size-1] = height[size-1]

    for i:=1;i<size;i++{
        leftDP[i] = max(leftDP[i-1],height[i])
    }
    for i:=size-2;i>=0;i--{
        rightDP[i] = max(rightDP[i+1],height[i])
    }
    for i:=1;i<size-1;i++{
        minHeight := min(leftDP[i],rightDP[i])
        waterVal :=minHeight-height[i]
        res +=waterVal
    }
    return res
}

func max(a,b int)int{
    if a>b{
        return a
    }
    return b
}
func min(a,b int)int{
    if a>b{
        return b
    }
    return a
}

3.单调栈解法

前面我们讲到，优化思路将问题转化为：给定一个数组，如何求得任意位置的左半边的最大值和右半边的最大值。
但仔细一想，其实我们并不需要找两侧最大值，只需要找到两侧最近的比当前位置高的柱子就行了。
针对这一类找最近值的问题，有一个通用解法：单调栈。
单调栈其实就是在栈的基础上，维持一个栈内元素单调。
在这道题，由于需要找某个位置两侧比其高的柱子（只有两侧有比当前位置高的柱子，当前位置才能接下雨水），我们可以维持栈内元素的单调递减。
PS. 找某侧最近一个比其大的值，使用单调栈维持栈内元素递减；找某侧最近一个比其小的值，使用单调栈维持栈内元素递增 …
当某个位置的元素弹出栈时，例如位置 a ，我们自然可以得到 a 位置两侧比 a 高的柱子：

• 一个是导致 a 位置元素弹出的柱子（ a 右侧比 a 高的柱子）
• 一个是 a 弹栈后的栈顶元素（a 左侧比 a 高的柱子）

当有了 a 左右两侧比 a 高的柱子后，便可计算 a 位置可接下的雨水量。

//单调栈法，核心考点
func trap(height []int) int {
    var stack []int
    var res int
    for i, v := range height {
        // 由于栈内是存放索引，并且栈内索引的高度值是递减的，
        for len(stack) > 0 && v > height[stack[len(stack)-1]] {
            // 拿出栈顶元素
            stacktop := stack[len(stack)-1]
            // 拿出就出栈，继续计算，出栈元素后的栈为了进入下一次循环继续计算
            stack = stack[:len(stack)-1]
            // 如果栈内没有元素了就需要继续添加
            if len(stack) == 0 {
                break
            }
            // 此时要计算两个索引边界，即碰到高于栈顶元素的索引，到栈顶元素的索引，用来计算面积
            // 这个地方为什么还要拿出栈顶元素来计算宽度呢？而不是用之前拿出来的栈顶元素计算呢？是因为假设出现一个类似于W的走势的话，中间低的索引都被出栈了，所以要计算长度也只能用栈内元素继续向前拿才是整确的索引。
            width := i - stack[len(stack)-1]-1
            // 而面积则是要由左右两边界的最小值来乘,这地方的高度就用heith来表示
            heith := min(height[stack[len(stack)-1]],v) - height[stacktop] 
            res += width*heith
        }
        // 在这里入栈，表明每次碰到的都是递减的高度
        stack = append(stack,i)
    }
    return res
}


func min(a, b int) int {
    if a < b {
        return a
    }else {
        return b
    }
}

4、双指针 时间O(N) 空间O(1)

在上述的动态规划方法中，我们用二维数组来存储每个柱子左右两侧的最大高度，但我们递推累加每个柱子的储水高度时其实只用到了 dp[i][0]和 dp[i][1] 两个值，因此我们递推的时候只需要用 int leftMax 和 int rightMax 两个变量就行了。
即将上述代码中的递推公式：
res += Math.min(dp[i][0], dp[i][1]) - height[i];
优化成：
res += Math.min(leftMax, rightMax) - height[i];
注意这里的 leftMax 是从左端开始递推得到的，而 rightMax 是从右端开始递推得到的。
因此遍历每个柱子，累加每个柱子的储水高度时，也需要用 left 和 right 两个指针从两端开始遍历。

//双指针，最优解法
func trap(height []int) int {
    if len(height) == 0 {
        return 0
    }
    left, right := 0, len(height)-1
    leftmax, rightmax := height[0], height[len(height)-1]
    var res int
    for ;left < right; {
        if rightmax > leftmax {
            res += leftmax - height[left]
            left ++
            if height[left] > leftmax {
                leftmax = height[left]
            }
        }else {
            res += rightmax - height[right]
            right--
            if height[right] > rightmax {
                rightmax = height[right]
            }
        }
    }
    return res
}