概述
开篇直接讲 Union-Find,然后以它为例,讲解如何使用科学方法研究算法性能。
编程作业是使用加权快速合并(Weighted Quick Union)解决渗滤(Percolation)问题。
建议阅读《算法 4th》的 1.4、1.5 两节。
开发高效算法的流程
建立问题模型
找出解决该问题大体上所需要的基本操作 ,据此找出算法解决该问题
算法是否足够快?是否满足对存储空间的要求 ?
如果不满足,我们就需要搞清楚 为什么会这样
想办法找出造成这些问题的源头 ,然后提出新的算法
如此循环直到满意为止
Quick-find

class QuickFindUF{private int[] _id;public QuickFindUF(int n){_id = new int[n];for (var i = 0; i < n; i++){_id[i] = i;}}public bool Connected(int p, int q){return _id[p] == _id[q];}public void Union(int p, int q){var pId = _id[p];var qId = _id[q];for (var i = 0; i < _id.Length; i++){if (_id[i] == pId){_id[i] = qId;}}}}

合并操作代价太大,特别是如果你需要在 N 个对象上 进行 N 次合并操作时,单是判断它们是否连通 就需要正比于 N^2 的时间。
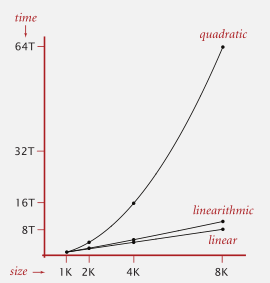
对于大型问题 ,我们不能接受需要平方时间的算法,因为它们无法成比例适应大规模问题。
Quick-union
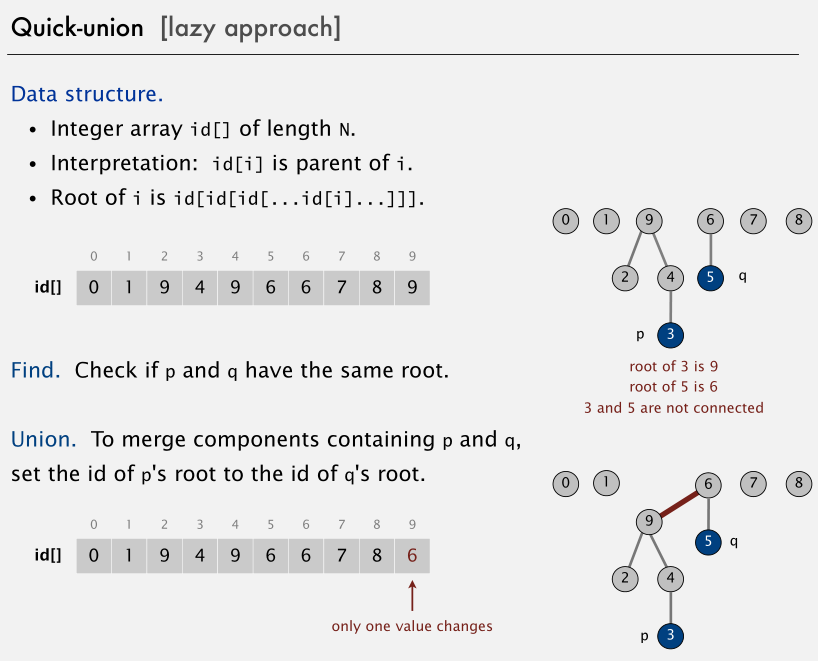
public class QuickUnionUF{private int[] _id;public QuickUnionUF(int n){_id = new int[n];for (var i = 0; i < n; i++){_id[i] = i;}}private int Root(int i){while (i!=_id[i]){i = _id[i];}return i;}public bool Connected(int p, int q){return Root(p) == Root(q);}public void Union(int p, int q){var i = Root(p);var j = Root(q);_id[i] = j;}}

快速合并的缺点在于树可能太高了,导致查找操作代价太大。你可能需要回溯一棵瘦长的树,每个对象只是指向下一个节点,那么对叶子节点执行一次查找操作,需要回溯整棵树。只进行查找操作就需要花费 N 次数组访问。
改进 Quick-union
带权
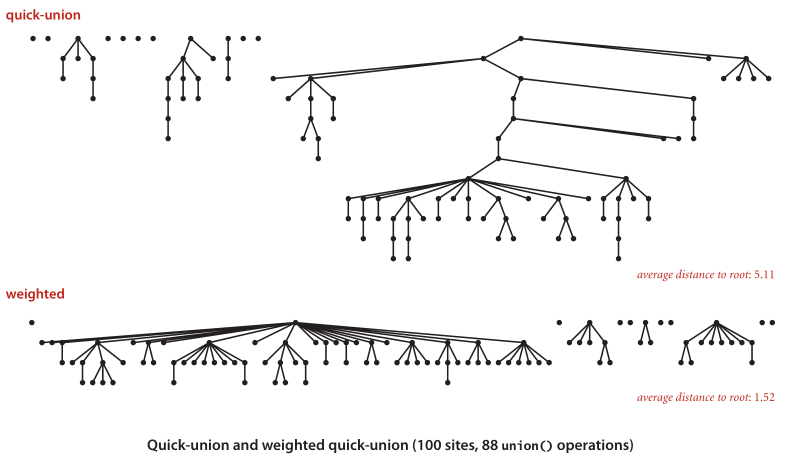

带权的树中任意节点的深度是 lg2(N)。
路径压缩
将树展平,当我们找到P的根节点之后,可以回过头来将路径上每个节点都指向根节点。

实际实现时只需将路径上的每个节点指向它的祖父节点,这种实现效果不如完全展平,但实际应用中两者差不多一样好。
Union-find applications

Percolation
渗滤(Percolation)是一个被数学模型精确描述的问题,没有人知道这个数学问题的解,我们有的唯一的解来自计算模型。
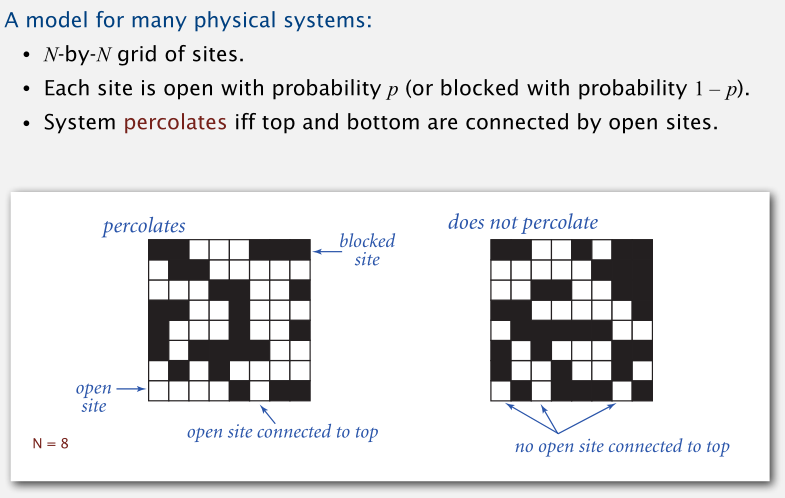
渗滤问题的重点在于找到 N 极大时,引起渗滤系统“相变”的 p 值。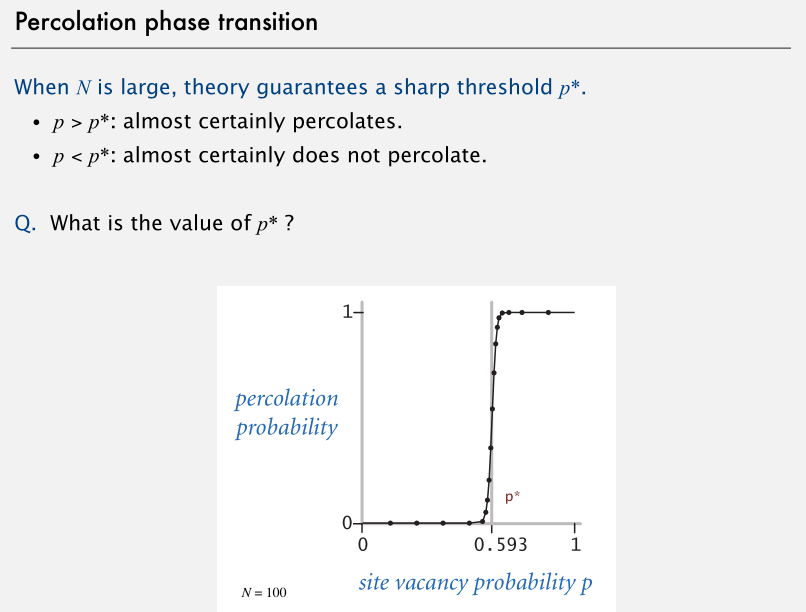
直接使用 Union-find 的问题在于,检查 top 行和 bottom 行的连通性时,它需要调用查找 N^2 次来依次检查 top 行每位,与 bottom 行每位的连通性。这是一个需要平方时间的暴力算法,太慢了。
解决方法时给 top 行和 bottom 行的分别引入一个虚拟位。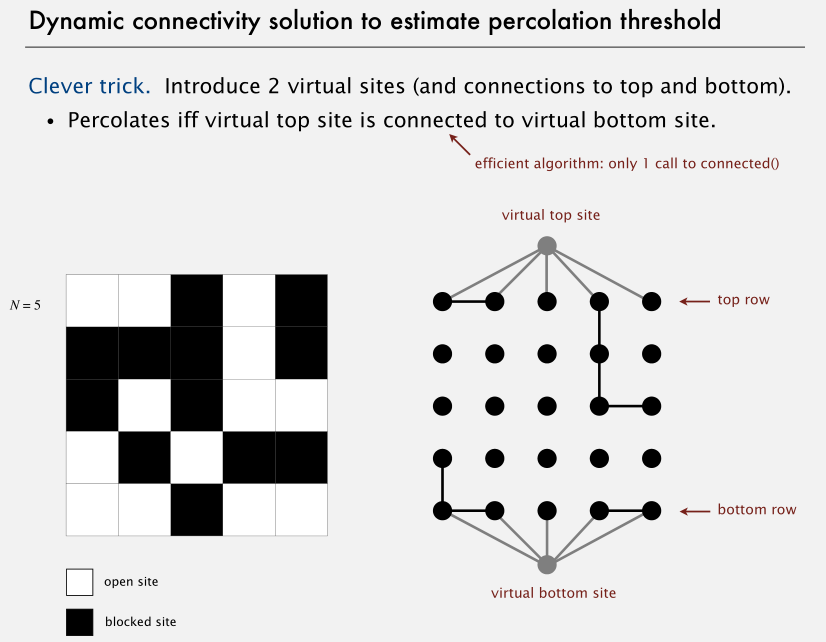
总结
我们选取了一个重要的问题——动态连通性问题
我们通过对问题建模试图精确理解,我们需要什么样的数据结构和算法来解决它
然后我们先提出了几个可以解决问题的简单算法
并很快发现它们不足以处理巨大问题
但之后我们发现了如何改进它们,得到了高效的算法
最后我们遇到了必须使用高效算法才能解决的应用问题


