概述

算法性能分析的基础是科学方法。本节我们首先通过实验观测程序运行时间（观察法），再依据实验结果提出关于性能的假设。接下来，我们创建数学模型来解释算法的行为。最后我们学习分析 Java 程序的内存使用情况。

AnalysisOfAlgorithms.pdf

学习目标

Define tilde and order-of-growth notations.
Determine the order of growth of the running time of a program as a function of the input size.
Formulate a hypothesis for the running time of a program as a function of the input size by performing computational experiments.
Calculate the amount of memory that a Java program uses a function of the input size.
Describe the binary search algorithm.
Analyze the running time of binary search.

Introduction

分析算法时要从多个角度来思考。
总的来说， 我们将要从多种不同的角色来思考这些问题 ：

1. 第一个角色是程序员, 他需要解决一个问题，让算法能够工作，并部署它

2. 第二个角色是用户，他想要完成某项工作，但不关心程序做了什么

3. 第三个角色是理论家，他真的想要理解发生的事情

4. 最后一个角色，是一个团队，团队中的基本工作有时需要，完成以上所有的工作

所以，今天的课程中每一种角色的工作都会出现一些。

实际上，你还是个学生时，你必须想到某一天你将会扮演这里任何一种甚至所有的角色。所以理解不同的观点是相当重要的。

分析算法的理由：

• 预测算法的性能

• 我们还想要比较完成同一任务不同算法的性能

• 并能得知在最坏情况下算法性能的底线

• 同时，我们需要理解关于算法如何运行的一些理论基础

但是首先，我们想要分析并理解算法的很实际的原因是为了避免性能错误。

分析算法的关键就在于运行时间，下面介绍了两个将 N^2 步骤缩减为 N*log2(N) 的成功算法。

FFT 和 Andrew Appel 的模拟 N 体之间的引力相互作用的算法。前者带来了数字多媒体技术，后者使科学家能够运行巨大N值的N体仿真 这个算法催生了新的研究。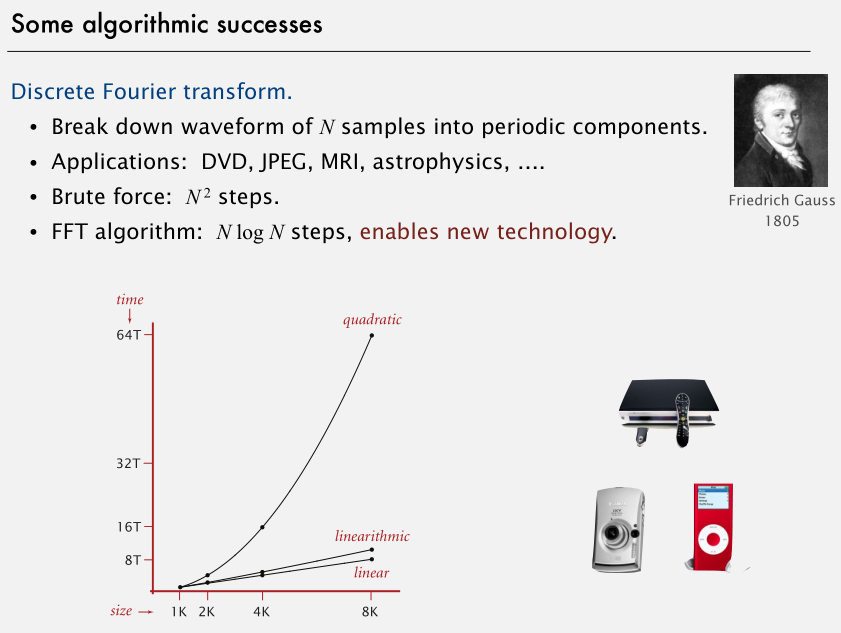

使用科学的方法来分析算法性能，所以我们要做的是：

1. 从自然界中观察某些特征。对我们来说，就是程序在计算机上的运行时间

2. 然后我们要提出假设——一些与观察到的现象相一致的模型

3. 而且我们希望假设是合理的并且能够让我们做一些预测 一般用来预测更大问题规模或者另一台计算机上的运行时间

4. 接下来我们会做更多的观察来验证预测

5. 直到，我们的模型假设和观察都吻合

证实我们的模型假设是正确的，这是一种理解程序性能的方法。使用科学方法，有一些基本原则。第一，如果要做实验，你应该期望 别人做同样的实验也能有相同的结果。而假设必须具有某个特殊的性质，它能被实验证伪。

Observations

以 3-Sum 问题的暴力解法为例，阐释如何使用观察法分析算法性能，并讲解了观察法的优势。

3-SUM

3-SUM 问题：给定 N 个不同整数，计算有多少种三个元素和为零的搭配。

暴力解法：

static int Count(int[] a)
{
    var n = a.Length;
    var count = 0;
    for (var i = 0; i < n; i++)
    {
        for (var j = i + 1; j < n; j++)
        {
            for (var k = j + 1; k < n; k++)
            {
                if (a[i] + a[j] + a[k] == 0) count++;
            }
        }
    }
    return count;
}

计时

通过 Stopwatch 进行计时。

static void Main(string[] args)
{
    const int n = 2000;
    var ints = Enumerable.Range(-n / 2, n).ToArray();
    var sw = new Stopwatch();
    sw.Start();
    var count = Count(ints);
    Console.WriteLine($"StopWatch:{sw.ElapsedMilliseconds}\tCount:{count}");
    Console.ReadKey();
}

作图分析

通过将每次的输入翻倍，得出 N 与 time 的离散值，再根据离散值绘图。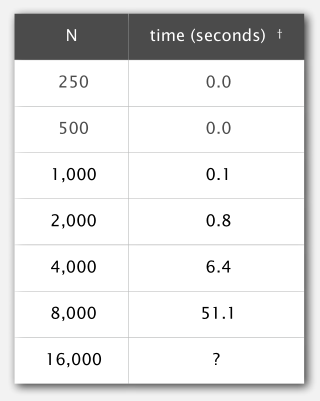

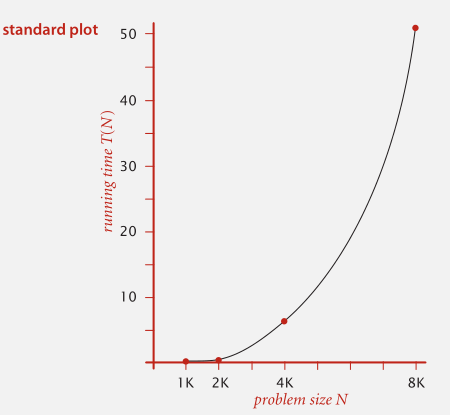
使用以 2 为底的双对数坐标进行绘图。在双对数坐标下，我们一般会得到一条直线，此时直线的斜率就是重点。

通过回归拟合出来的直线斜率为 3，再计算出 b 和 c 到的经验值，得出假设。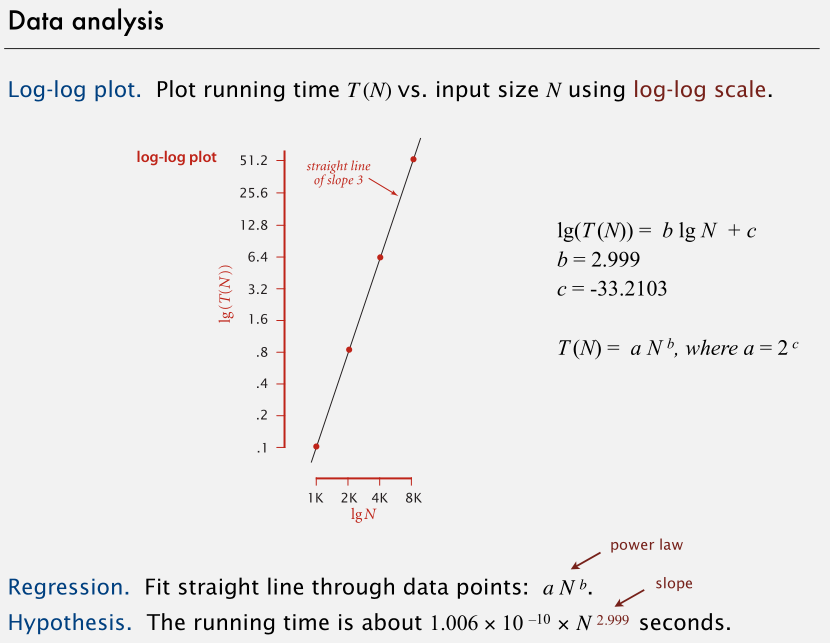

通过假设预测 N 为 16000 时的运行时间为 408.1 s，接着运行实验，测试实际运行时间。

Doubling hypothesis

绝大多数计算机算法的运行时间满足幂定律。

下面我们假设该算法也满足幂定律。我们通过将输入翻倍，计算 N 和 2N 运行时间的比率，进而计算幂定律中的 b 值。

然后通过给定一个较大的 N，多次运行程序求出 a。

不难看出，这和我们通过作图得到的模型很接近。

算法的可实验性

我们只需运行大量实验，就可以计算出决定算法性能的关键因素和系统相关因素。不必像别的学科又是动物实验又是发射行星探测器那么麻烦。

Mathematical Models

建立近似数学模型的步骤：

1. 识别基本操作，确定基本操作的开销

2. 分析统计算法的基本操作和每个操作的频率

3. 简化统计方式

   1. cost model：仅统计最耗时的操作，其他操作直接忽略

   2. tilde notation：仅保留最高阶项

4. 近似模型

Cost of basic operations

绝大多数操作的耗时是常数。有些操作的耗时和所处理对象数 N 成正比，例如分配一个大小为 N 的数组，需要正比于N的时间。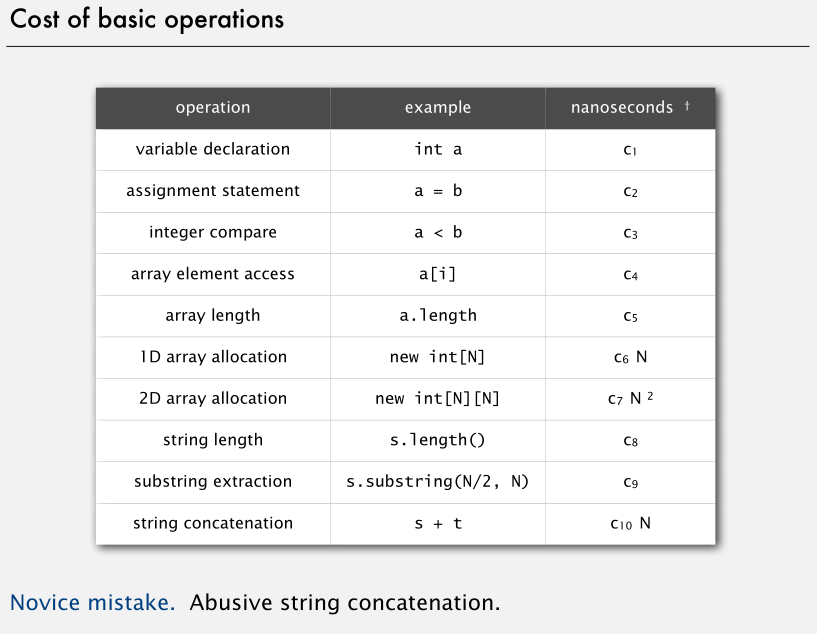

注：字符串连接操作的运行时间与字符串的长度成正比，不是常数时间。

Simplifying the calculations

以统计 2-SUM 中的 array access 操作频率为例。

通过离散求和不难算出 if (a[i] + a[j] == 0) 语句共执行 N(N-1)/2 次，每次都需要读取 a[i] 和 a[j] 就是 2 次读取操作，所以最终计算出的 array access 频率是 N(N-1)。

Simplification 1: cost model

与其钻到程序里抠细节，我们用开销最大频率最高的操作来代表执行时间。

一般，我们假设实际的运行时间就是常数乘以这个操作的执行时间。所以这个例子中，我们选择访问数组作为代表。

Simplification 2: tilde notation

第二个简化是忽略推导出的式子中的低阶项。

这种简化的思想就是当式子中的 N 很大时，N^3 项远大于 N^2 项和常数项。实际上，大到几乎注意不到低阶项。所以这些式子都可以近似为 1/6 N^3。

丢掉这些低阶项极大地简化了计算。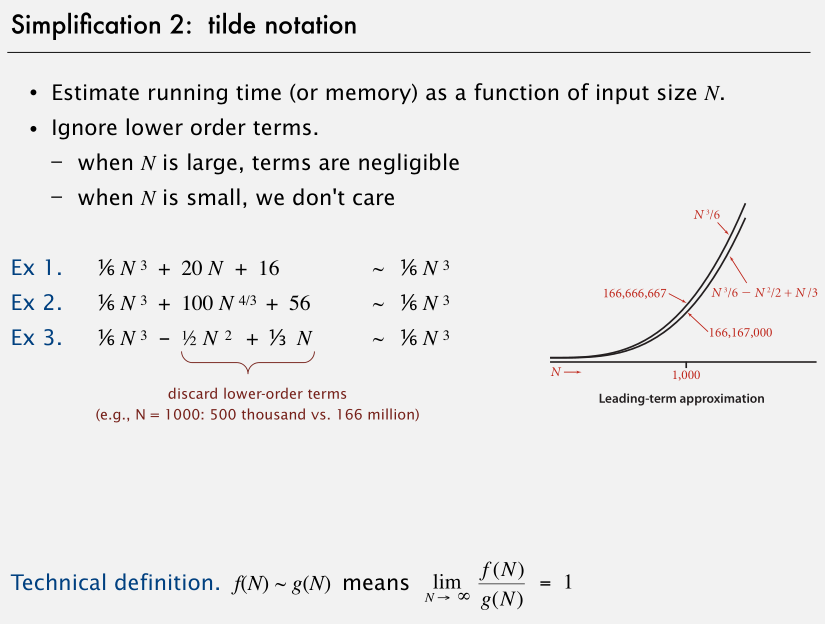

~ 号的严格定义：专注于一种操作，丢掉低阶项。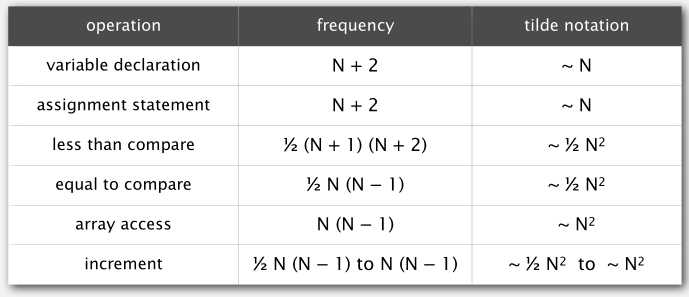

注：N 很小时，低阶项是不能忽略的。不过我们不是很关心，因为我们想要做的是对于大 N 估计运行时间，小 N 的运行时间本来就不长。

Example: 3-SUM

以 3-SUM 为例，演示 cost model 和 tilde notation 的运用。

3-SUM 有三重循环，其 if 语句的执行次数是个组合数学问题，我们要求的是从 N 个对象中选出 3 个的方法，这是个二项式系数 Cn3，它近似为 1/6 N^3 。

每次执行 if 语句访问数组三次，那么就是 1/2 N^3。

我们不会计算所有操作的开销，这太麻烦了。我们选出开销最大的操作乘上频率并作出近似来试图为运行时间建立一个好模型。

Estimating a discrete sum

这门课中我们不会教完整的离散数学，但要介绍一些我们要用到的离散数学基础知识，它们并不难理解。

很多时候我们需要估计一个离散求和，像我们做过的从 1 到 N 的求和，或者平方的求和，或者其他例如三重循环这样的。

实际上，如果你学过微积分基础，可以将求和替换为积分。我们做一些计算然后应用欧拉-麦克劳林求和公式来得到真正的近似。

Mathematical models for running time

总的来说，实际上在数学建模时我们可以运用高级的数学知识建立精确的模型，获得复杂的式子。但这些都是理论家擅长的，对于刚接触算法的人可能并不懂得这些，所以精确的模型最好还是留给那些专家。

对于我们涉及的所有算法，我们都会试着用合适的近似模型来描述运行时间。有时我们会给出数学证明，其他时候我们只是引用专家的工作成果。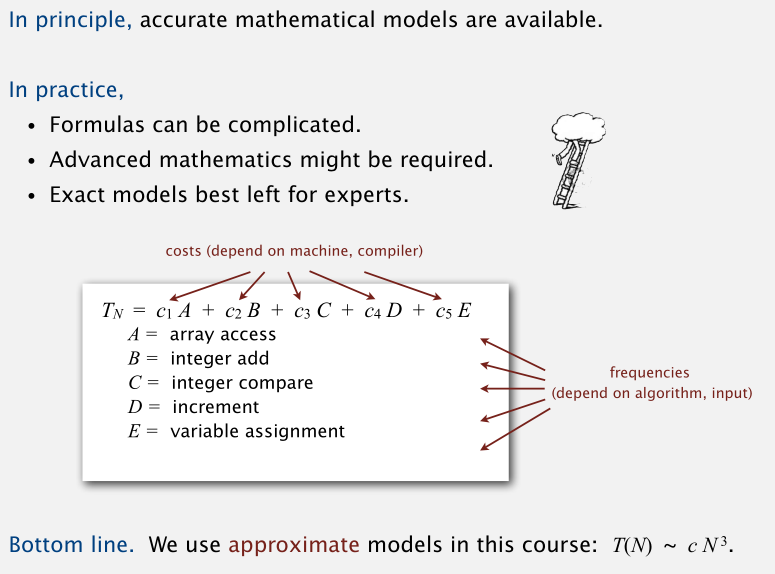

Order of Growth Classifications

增长阶数

最多能接受 NlogN 的算法，增长阶数在平方阶和以上的算法，在 N 很大时基本无法使用。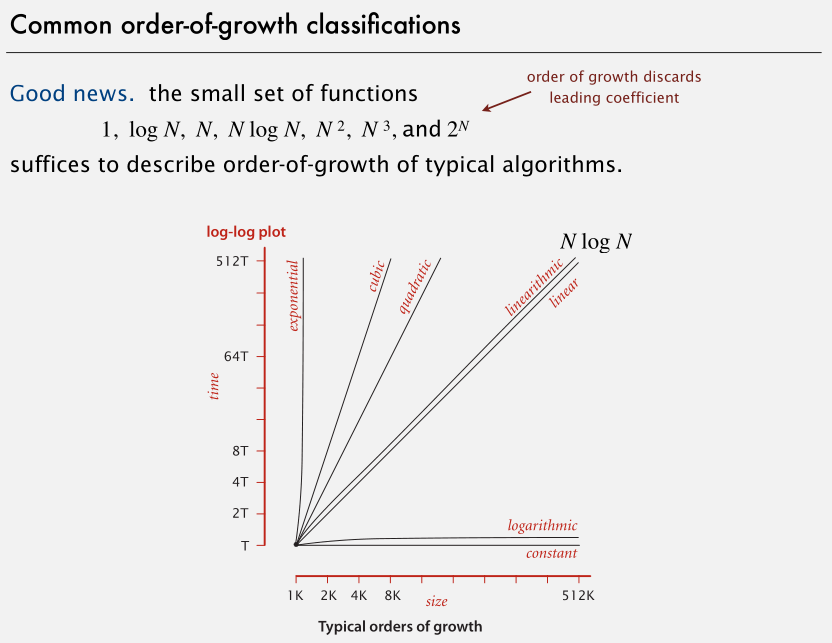

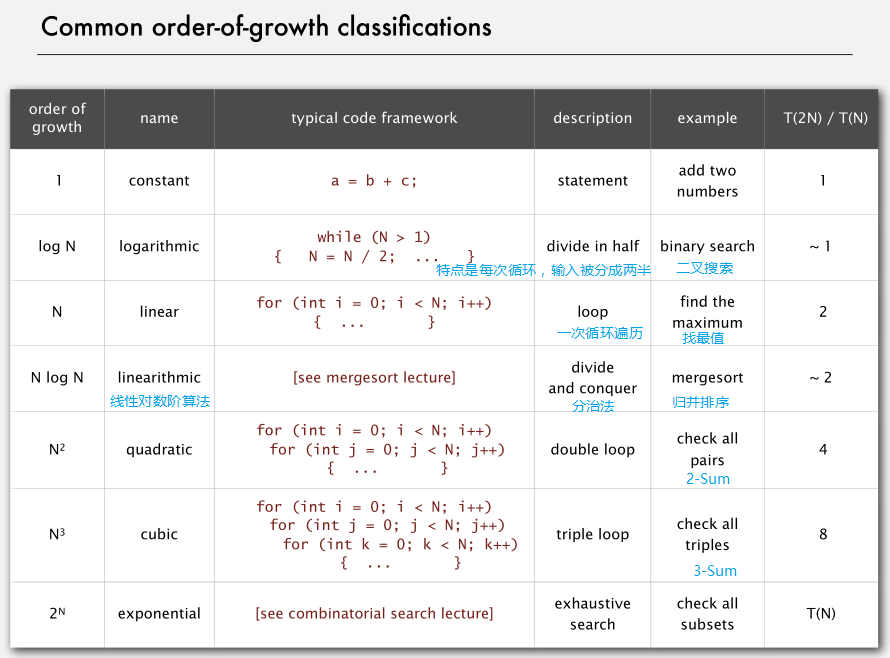
增长阶数的现实意义：
早期还有讨论平方阶算法是否有用的，随着时代的发展，虽然计算机性能大幅提升，但输入数据 N 的增长更为迅速。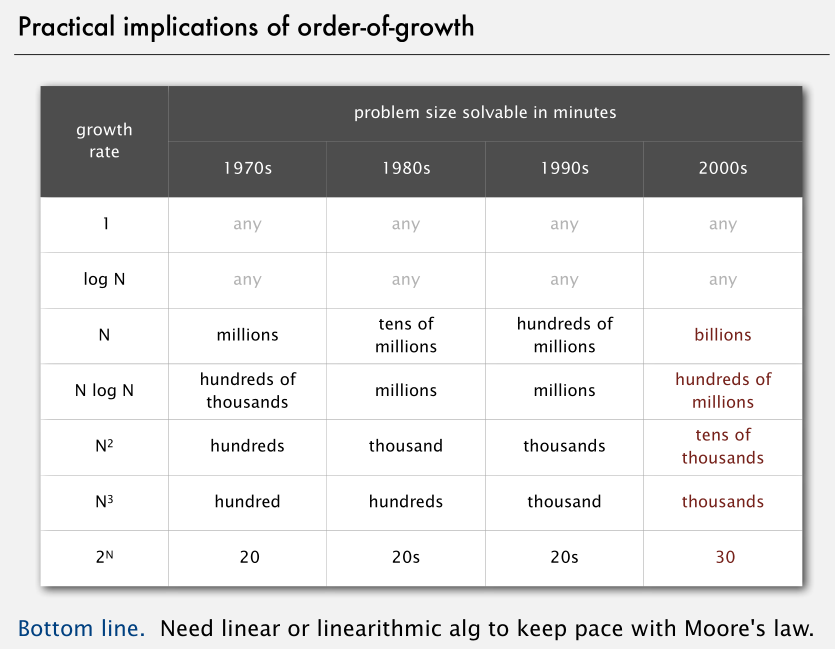

二叉搜索

演示了二叉搜索：

二叉搜索的 Java 实现：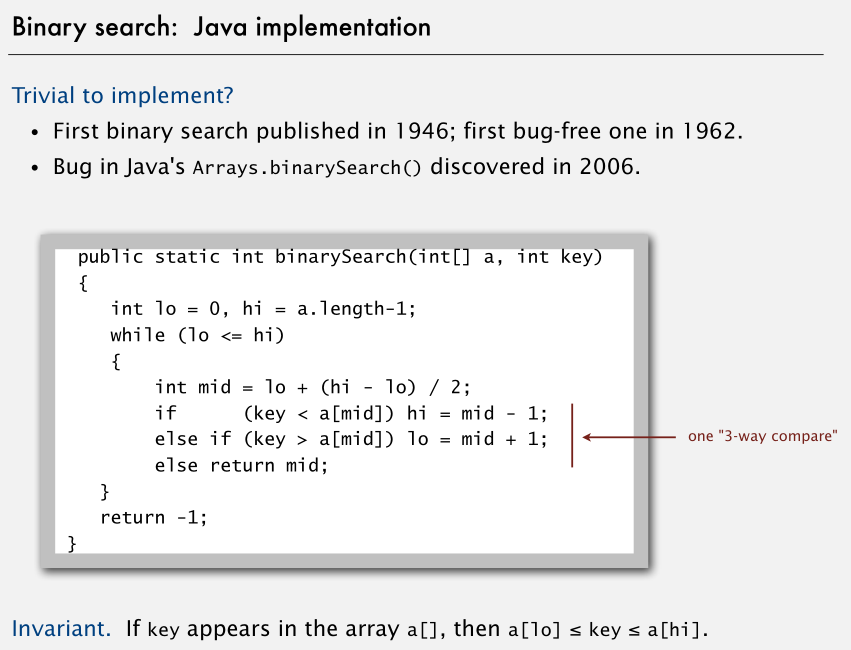

二叉搜索的数学分析：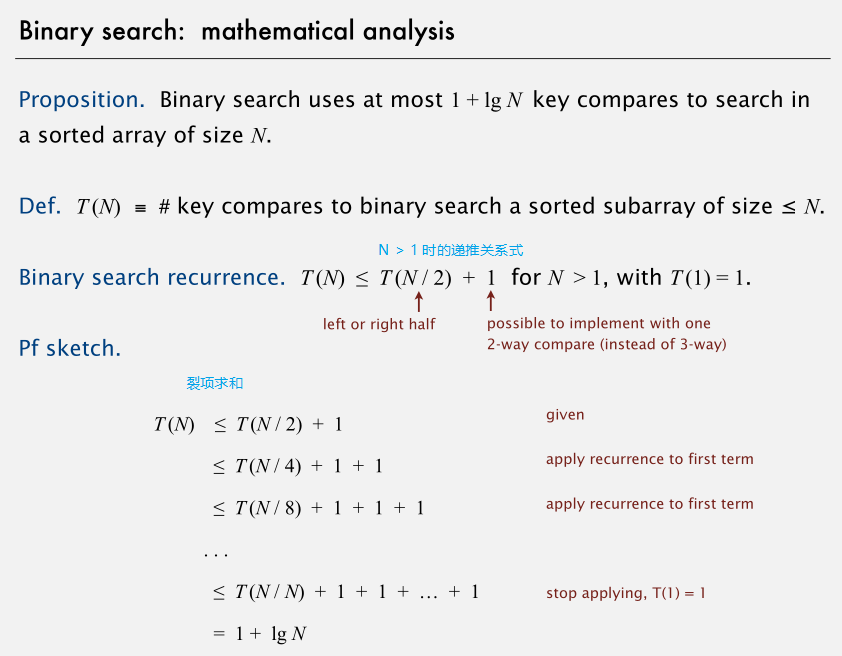

此处只考虑了 N 为偶数的情况，N 为奇数的情况下 T(N) 也正比于 lgN。

基于搜索的 3-Sum 算法

1. 先排序，排序需要 NlgN 的时间

2. 每两个数组成一对，通过二叉搜索去找 -(a[i] + a[j])

3. 记得排除 i，j，k 有重复值的情况

通过测试，比较改进后的算法效率。

Theory of Algorithms

伴随输入的不同，算法代价有着上界、下界和平均值。

虽然输入不同会造成算法代价的波动，但我们关心的是客户要解决的实际问题，实际情况。

设计算法时，一般有两种方式计算算法代价：

1. 考虑最坏的情况

2. 依靠某种概率，考虑随机情况

用于描述性能界限的常用记号：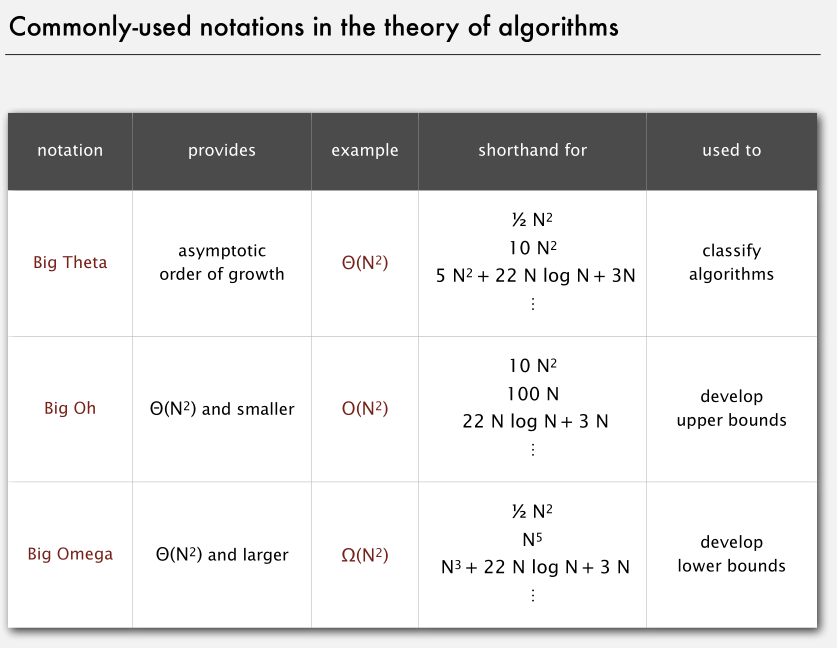

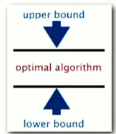
对于 1-Sum 问题，暴力算法的 Upper bound == Lower bound，即证明了 1-Sum 的暴力算法是最优的：

对于 3-Sum 问题，我们已知一个较好的上界，我们也能证明最好的下界是 Ω(N)，但没人能找到更高的下界。这便使得上界与下界间存在间隔，即我们不知道 3-Sum 的最优算法。3-Sum 就是算法理论中一个开放问题的例子。

1. 研究算法时并不执着于最坏情况，我们更应该专注于理解输入的性质，并针对输入的性质寻找高效的算法

2. 真的要预测性能和比较算法时，我们需要比常数因子级误差更准确的分析

Recall that big-Oh notation provides only an upper bound on the growth rate of a function as nn gets large. In this course, we primarily use tilde notation because it more accurately describes the function—it provides both an upper and lower bound on the function as well as the coefficient of the leading term.

Memory

基础常识：

Java 实现中基本类型及数组的内存需求：

• Object overhead 16 bytes：对象需要的额外空间

• Reference 8 bytes：引用的开销

• Padding：典型实现中内置的用来对齐的空间，使得每个对象占据的空间是 8 字节的倍数

例一：Date 对象的大小是 32 bytes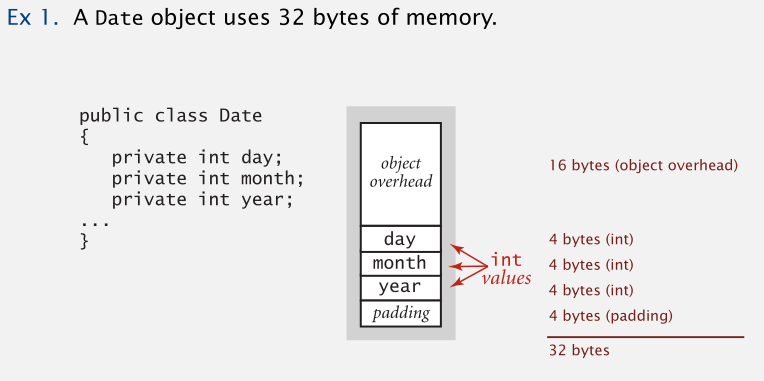

例二：长度为 N 的字符串的空间开销是 2N + 64 字节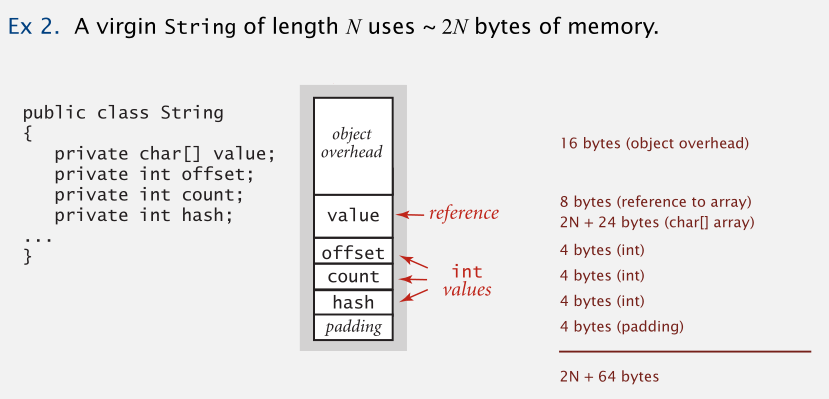

简单分析内存使用时，不必考虑引用开销：

示例：分析 WeightedQuickUnionUF 的内存开销。

1. WeightedQuickUnionUF 类本身的 Object overhead

2. int[] id 和 int[] sz 数组，每个引用开销 8 字节，数组开销 4N +24 字节

3. count 4 字节

4. padding 4 字节

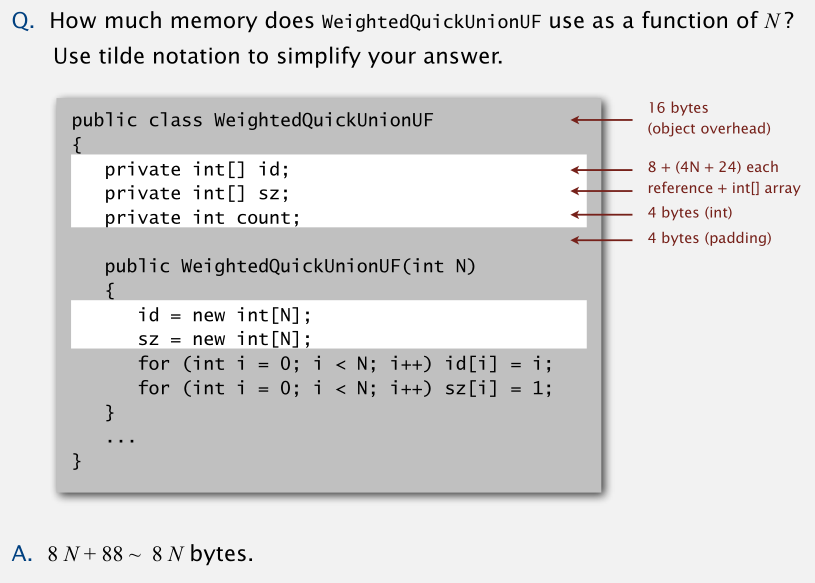
总结