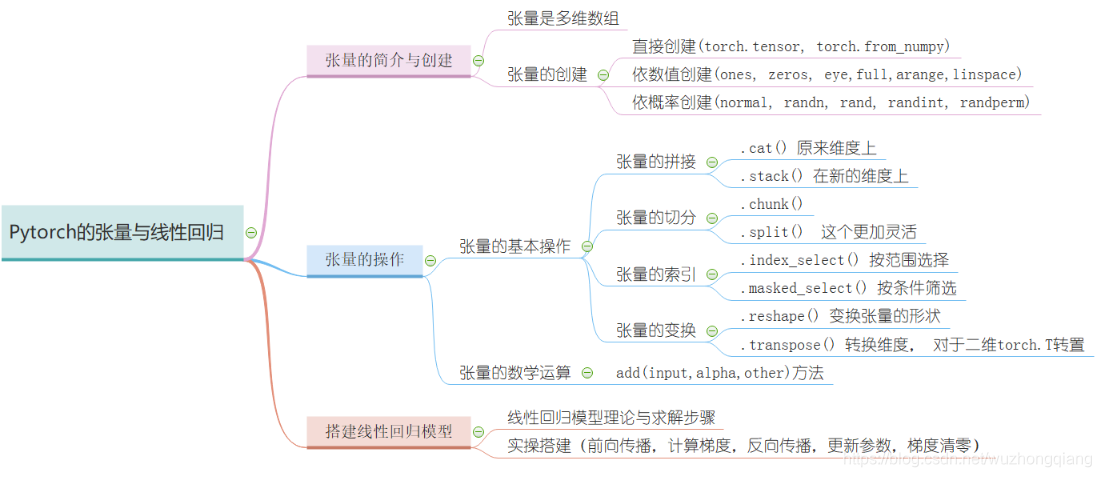
张量的简介与创建

这部分内容介绍 pytorch 中的数据结构——Tensor，Tensor 是 PyTorch 中最基础的概念，其参与了整个运算过程，主要介绍张量的概念和属性，如 data, device, dtype 等，并介绍 tensor 的基本创建方法，如直接创建、依数值创建和依概率分布创建等。

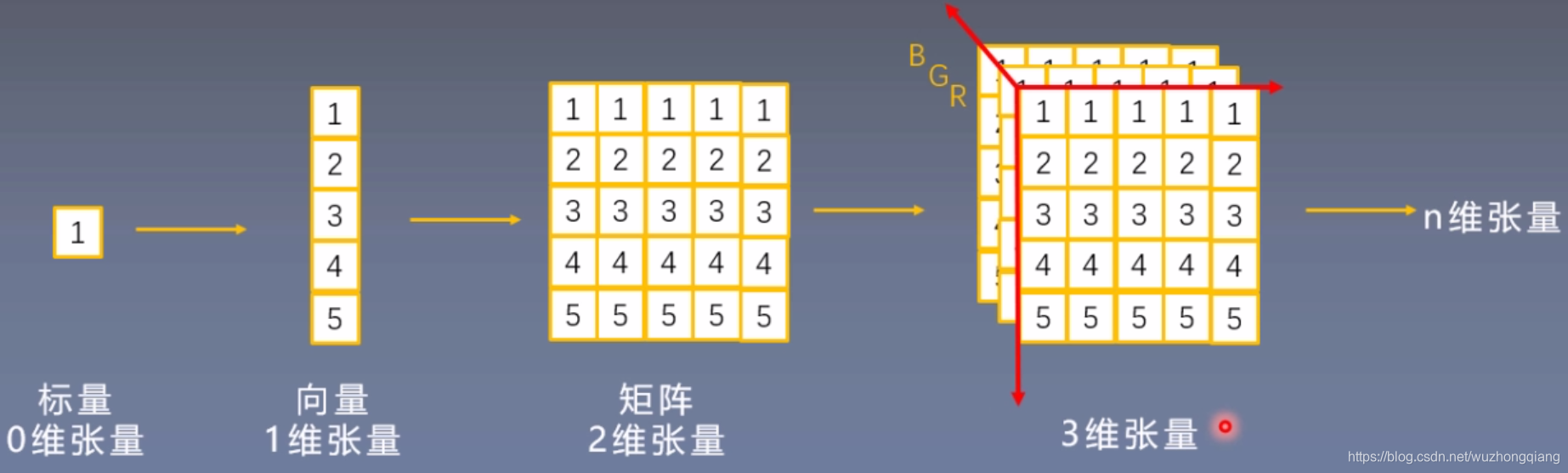
张量简介

张量的基本概念

张量其实是一个多维数组，它是标量、向量、矩阵的高维拓展
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图1

Tensor 与 Variable

在 Pytorch0.4.0 版本之后其实 Variable 已经并入 Tensor， 但是 Variable 这个数据类型的了解，对于理解张量来说很有帮助， 这到底是个什么呢？
Variable 是 torch.autograd 中的数据类型。
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图2

Variable 有下面的 5 个属性：

  • data: 被包装的 Tensor
  • grad: data 的梯度
  • grad_fn: fn 表示 function 的意思，记录我么创建的创建张量时用到的方法，比如说加法，乘法，这个操作在求导过程需要用到，Tensor 的 Function， 是自动求导的关键
  • requires_grad: 指示是否需要梯度， 有的不需要梯度
  • is_leaf: 指示是否是叶子节点（张量）

这些属性都是为了张量的自动求导而设置的， 从 Pytorch0.4.0 版开始，Variable 并入了 Tensor， 看看张量里面的属性：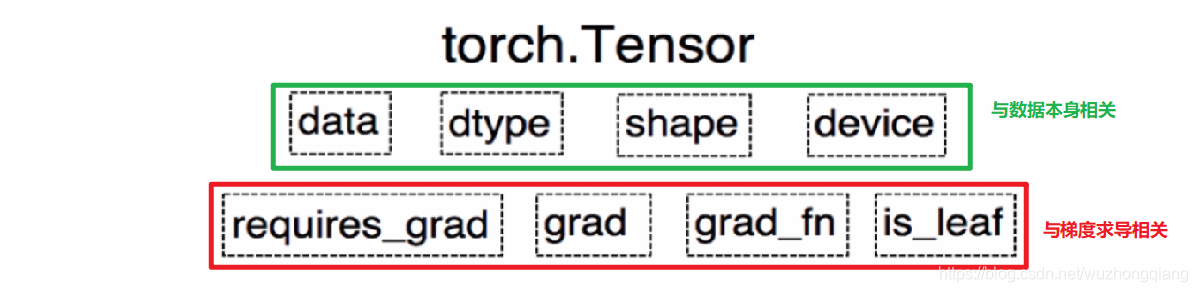
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图3

可以发现，如今版本里面的 Tensor 共有 8 个属性，上面四个与数据本身相关，下面四个与梯度求导相关。 其中有五个是 Variable 并入过来的， 这些含义就不解释了， 而还有三个属性没有说：

  • dtype: 张量的数据类型， 如 torch.FloatTensor, torch.cuda.FloatTensor, 用的最多的一般是 float32 和 int64(torch.long)
  • shape: 张量的形状， 如 (64, 3, 224, 224)
  • device: 张量所在的设备， GPU/CPU， 张量放在 GPU 上才能使用加速。

知道了什么是张量，那么如何创建张量呢？

张量的创建

直接创建张量

torch.Tensor(): 功能： 从 data 创建 Tensor
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图4

  • data，就是我们的数据，可以是 list，也可以是 numpy。
  • dtype 这个是指明数据类型， 默认与 data 的一致。
  • device 是指明所在的设备
  • requires_grad 是是否需要梯度， 在搭建神经网络的时候需要求导的那些参数这里要设置为 true。
  • pin_memory 是否存于锁页内存，这个设置为 False 就可以。

下面就具体代码演示：

  1. arr = np.ones((3, 3))
  2. print('ndarry的数据类型：', arr.dtype)
  4. t = torch.tensor(arr, device='cuda')
  5. print(t)
  8. ndarry的数据类型： float64
  9. tensor([[1., 1., 1.],
  10.     [1., 1., 1.],
  11.     [1., 1., 1.]], device='cuda:0', dtype=torch.float64)

通过 numpy 数组创建

torch.from_numpy(ndarry): 从 numpy 创建 tensor
注意：这个创建的 Tensor 与原 ndarray共享内存, 当修改其中一个数据的时候，另一个也会被改动。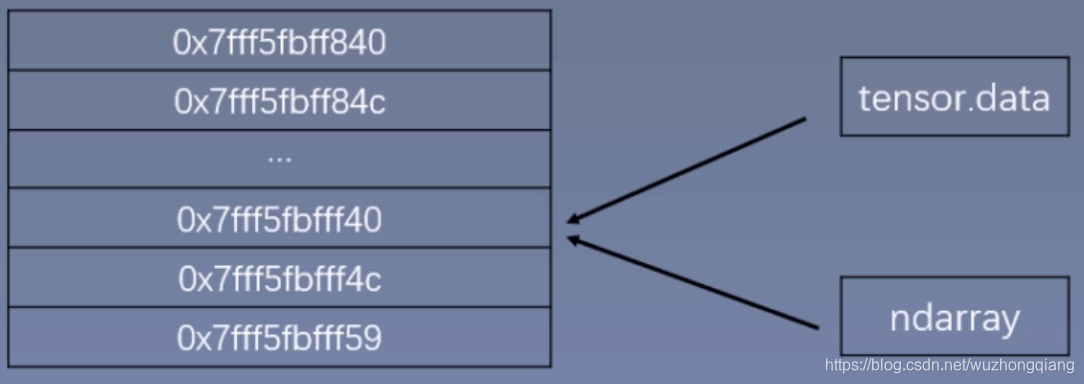
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图5
下面具体看代码演示（共享内存）：

  1. arr = np.array([[1, 2, 3], [4, 5, 6]])
  2. t = torch.from_numpy(arr)
  4. print(arr, '\n',t)
  5. arr[0, 0] = 0
  6. print('*' * 10)
  7. print(arr, '\n',t)
  8. t[1, 1] = 100
  9. print('*' * 10)
  10. print(arr, '\n',t)
  13. [[1 2 3]
  14.  [4 5 6]] 
  15.  tensor([[1, 2, 3],
  16.         [4, 5, 6]], dtype=torch.int32)
  17. **********
  18. [[0 2 3]
  19.  [4 5 6]] 
  20.  tensor([[0, 2, 3],
  21.         [4, 5, 6]], dtype=torch.int32)
  22. **********
  23. [[  0   2   3]
  24.  [  4 100   6]] 
  25.  tensor([[  0,   2,   3],
  26.         [  4, 100,   6]], dtype=torch.int32)

依据数值创建

  • torch.zeros(): 依 size 创建全 0 的张量

系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图6

  • layout 这个是内存中的布局形式， 一般采用默认就可以。
  • out，表示输出张量，就是再把这个张量赋值给别的一个张量，但是这两个张量是一样的，指的同一个内存地址。看代码：```python out_t = torch.tensor([1]) t = torch.zeros((3, 3), out=out_t)

print(out_t, ‘\n’, t) print(id(t), id(out_t), id(t) == id(out_t))

tensor([[0, 0, 0], [0, 0, 0], [0, 0, 0]]) tensor([[0, 0, 0], [0, 0, 0], [0, 0, 0]]) 2575719258696 2575719258696 True

  3. - torch.zeros_like(input, dtype=None, layout=None, device=None, requires_grad=False) : 这个是创建与 input 同**形状**的全 0 张量```python
  4. t = torch.zeros_like(out_t)   
  5. print(t)
  7. tensor([[0, 0, 0],
  8.         [0, 0, 0],
  9.         [0, 0, 0]])
  • 除了全 0 张量， 还可以创建全 1 张量， 用法和上面一样，torch.ones(), torch.ones_like()， 还可以自定义数值张量：torch.full(), torch.full_like()

系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图7
这里的 fill_value 就是要填充的值。

  1. t = torch.full((3,3), 10)
  2. tensor([[10., 10., 10.],
  3.         [10., 10., 10.],
  4.         [10., 10., 10.]])
  • torch.arange(): 创建等差的 1 维张量，数值区间[start, end)， 注意这是右边开，取不到最后的那个数。

系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图8
这个和 numpy 的差不多，这里的 step 表示的步长。

  1. t = torch.arange(2, 10, 2)
  • torch.linspace(): 创建均分的 1 维张量， 数值区间[start, end] 注意这里都是闭区间，和上面的区分。

系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图9
这里是右闭， 能取到最后的值，并且这里的 steps 是数列的长度而不是步长。

  1. t = torch.linspace(2, 10, 5)   
  4. t = torch.linspace(2, 10, 6)

除了创建均分数列，还可以创建对数均分数列：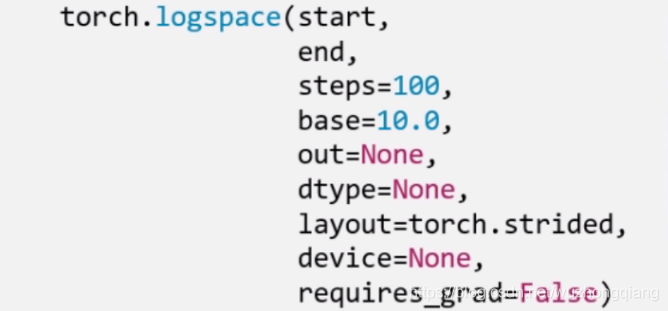
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图10
这里的 base 表示以什么为底。

  • torch.eye(): 创建单位对角矩阵， 默认是方阵

系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图11
n, m 分别是矩阵的行数和列数。

依概率分布创建张量

torch.normal(): 生成正态分布（高斯分布）， 这个使用的比较多
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图12
mean 是均值，std 是标准差。 但是这个地方要注意， 根据 mean 和 std，分别各有两种取值，所以这里会有四种模式：

  • mean 为标量， std 为标量
  • mean 为标量， std 为张量
  • mean 为张量， std 为标量
  • mean 为张量，std 为张量

这个看代码来的直接：

  1. t_normal = torch.normal(0, 1, size=(4,))
  2.                         print(t_normal)     
  5. std = torch.arange(1, 5, dtype=torch.float)
  6. print(std.dtype)
  7. t_normal2 = torch.normal(1, std)
  8. print(t_normal2)        
  11. mean = torch.arange(1, 5, dtype=torch.float)
  12. t_normal3 = torch.normal(mean, 1)
  13. print(t_normal3)     
  16. mean = torch.arange(1, 5, dtype=torch.float)
  17. std = torch.arange(1, 5, dtype=torch.float)
  18. t_normal4 = torch.normal(mean, std)
  19. print(t_normal4)

下面一个是标准正态分布：torch.randn(), torch.randn_like()
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图13
生成均匀分布：torch.rand(), rand_like() 在[0,1) 生成均匀分布
torch.randint(), torch.randint_like(): 区间[low,hight) 生成整数均匀分布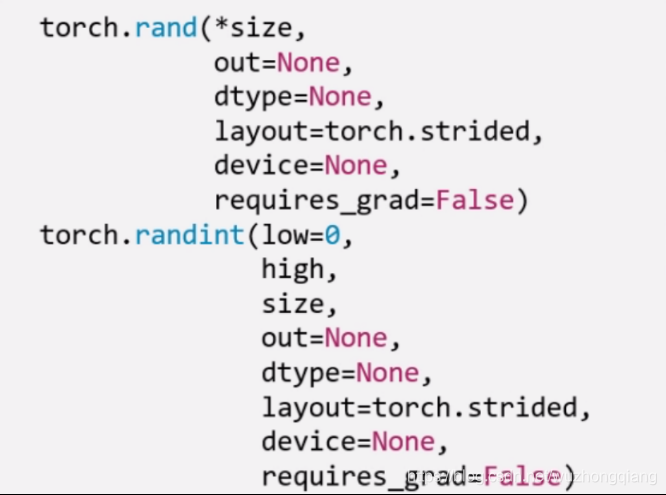
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图14
下面看最后两个：
torch.randperm(n): 生成从 0 - n-1 的随机排列, n 是张量的长度, 经常用来生成一个乱序索引。
torch.bernoulli(input): 以 input 为概率，生成伯努利分布 (0-1 分布，两点分布）， input: 概率值
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图15

张量的操作

这次整理张量的基本操作，比如张量的拼接，切分，索引和变换以及数学运算等，并基于所学习的知识，实现线性回归模型。

张量的基本操作

1. 张量的拼接

  • torch.cat(tensors, dim=0, out=None): 将张量按维度 dim 进行拼接, tensors 表示张量序列， dim 要拼接的维度
  • torch.stack(tensors, dim=0, out=None): 在新创建的维度 dim 上进行拼接， tensors 表示张量序列， dim 要拼接的维度

stack 会新创建一个维度，然后完成拼接。还是看代码：

  1. t = torch.ones((2, 3))
  2. print(t)
  4. t_0 = torch.cat([t, t], dim=0)       
  5. t_1 = torch.cat([t, t], dim=1)    
  6. print(t_0, t_0.shape)
  7. print(t_1, t_1.shape)
  9. tensor([[1., 1., 1.],
  10.     [1., 1., 1.]])
  11. tensor([[1., 1., 1.],
  12.     [1., 1., 1.],
  13.     [1., 1., 1.],
  14.     [1., 1., 1.]]) torch.Size([4, 3])
  15. tensor([[1., 1., 1., 1., 1., 1.],
  16.     [1., 1., 1., 1., 1., 1.]]) torch.Size([2, 6])

cat 是在原来的基础上根据行和列，进行拼接， 我发现一个问题，就是浮点数类型拼接才可以，long 类型拼接会报错。
下面我们看看stack 方法：

  1. t_stack = torch.stack([t,t,t], dim=0)
  2. print(t_stack)
  3. print(t_stack.shape)
  5. t_stack1 = torch.stack([t, t, t], dim=1)
  6. print(t_stack1)
  7. print(t_stack1.shape)
  10. tensor([[[1., 1., 1.],
  11.          [1., 1., 1.]],
  13.         [[1., 1., 1.],
  14.          [1., 1., 1.]],
  16.         [[1., 1., 1.],
  17.          [1., 1., 1.]]])
  18. torch.Size([3, 2, 3])
  19. tensor([[[1., 1., 1.],
  20.          [1., 1., 1.],
  21.          [1., 1., 1.]],
  23.         [[1., 1., 1.],
  24.          [1., 1., 1.],
  25.          [1., 1., 1.]]])
  26. torch.Size([2, 3, 3])

stack 是根据给定的维度新增了一个新的维度，在这个新维度上进行拼接, 这个. stack 与其说是从新维度上拼接，不太好理解，其实是新加了一个维度 Z 轴，只不过 dim=0 和 dim=1 的视角不同罢了。 dim=0 的时候，是横向看，dim=1 是纵向看。
所以这两个使用的时候要小心，看好了究竟是在原来的维度上拼接到一块，还是从新维度上拼接到一块。

2. 张量的切分

torch.chunk(input, chunks, dim=0): 将张量按维度 dim 进行平均切分， 返回值是张量列表，注意，如果不能整除， 最后一份张量小于其他张量。 chunks 代表要切分成几份。 下面看一下代码实现：

  1. a = torch.ones((2, 7))  
  2. list_of_tensors = torch.chunk(a, dim=1, chunks=3)   
  3. print(list_of_tensors)
  4. for idx, t in enumerate(list_of_tensors):
  5.     print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))
  8. (tensor([[1., 1., 1.],
  9.         [1., 1., 1.]]), tensor([[1., 1., 1.],
  10.         [1., 1., 1.]]), tensor([[1.],
  11.         [1.]]))
  12. 第1个张量：tensor([[1., 1., 1.],
  13.         [1., 1., 1.]]), shape is torch.Size([2, 3])
  14. 第2个张量：tensor([[1., 1., 1.],
  15.         [1., 1., 1.]]), shape is torch.Size([2, 3])
  16. 第3个张量：tensor([[1.],
  17.         [1.]]), shape is torch.Size([2, 1])

torch.split(tensor, split_size_or_sections, dim=0): 这个也是将张量按维度 dim 切分，但是这个更加强大， 可以指定切分的长度， split_size_or_sections 为 int 时表示每一份的长度， 为 list 时，按 list 元素切分```

t = torch.ones((2, 5))

list_of_tensors = torch.split(t, [2, 1, 2], dim=1)
for idx, t in enumerate(list_of_tensors): print(“第{}个张量：{}, shape is {}”.format(idx+1, t, t.shape))

第1个张量：tensor([[1., 1.], [1., 1.]]), shape is torch.Size([2, 2]) 第2个张量：tensor([[1.], [1.]]), shape is torch.Size([2, 1]) 第3个张量：tensor([[1., 1.], [1., 1.]]), shape is torch.Size([2, 2])

  1. <br />所以切分，也有两个函数，.chunk 和. split。 
  3. - .chunk 切分的规则就是提供张量，切分的维度和几份， 比如三份， 先计算每一份的大小，也就是这个维度的长度除以三，然后上取整，就开始沿着这个维度切，最后不够一份大小的，也就那样了。 所以长度为 7 的这个维度，3 块，每块 7/3 上取整是 3， 然后第一块 3，第二块是 3，第三块 1。这样切
  4. - .split 这个函数的功能更加强大，它可以指定每一份的长度，只要传入一个列表即可，或者也有一个整数，表示每一份的长度，这个就根据每一份的长度先切着， 看看能切几块算几块。 不过列表的那个好使，可以自己指定每一块的长度，但是注意一下，这个长度的总和必须是维度的那个总长度才用办法切。
  5. <a name="oBbCY"></a>
  6. #### 3. 张量的索引
  7. torch.index_select(input, dim, index, out=None): 在维度 dim 上，按 index 索引数据，返回值，以 index 索引数据拼接的张量。```json
  8. t = torch.randint(0, 9, size=(3, 3))     
  9. print(t)
  10. idx = torch.tensor([0, 2], dtype=torch.long)   
  11. t_select = torch.index_select(t, dim=1, index=idx)  
  12. print(t_select)
  15. tensor([[3, 7, 3],
  16.     [4, 3, 7],
  17.     [5, 8, 0]])
  18. tensor([[3, 3],
  19.     [4, 7],
  20.     [5, 0]])


torch.masked_select(input, mask, out=None): 按 mask 中的 True 进行索引，返回值：一维张量。 input 表示要索引的张量， mask 表示与 input 同形状或者可以广播的布尔类型的张量。 这种情况在选择符合某些特定条件的元素的时候非常好使， 注意这个是返回一维的张量。下面看代码：``` mask = t.ge(5)
print(“mask: \n”, mask) t_select1 = torch.masked_select(t, mask)
print(t_select1)

mask: tensor([[False, True, False], [False, False, True], [ True, True, False]]) tensor([7, 7, 5, 8])

  1. <br />所以张量的索引，有两种方式：.index_select 和. masked_select
  3. - .index_select： 按照索引查找 需要先指定一个 Tensor 的索引量，然后指定类型是 long 的
  4. - .masked_select: 就是按照值的条件进行查找，需要先指定条件作为 mask
  5. <a name="czIgD"></a>
  6. #### 4. 张量的变换
  7. torch.reshape(input, shape): 变换张量的形状，这个很常用, input 表示要变换的张量，shape 表示新张量的形状。 但注意，当张量在内存中是连续时， 新张量与 input 共享数据内存```json
  8. t = torch.randperm(8)       
  9. print(t)
  11. t_reshape = torch.reshape(t, (-1, 2, 2))    
  12. print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
  14. t[0] = 1024
  15. print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
  16. print("t.data 内存地址:{}".format(id(t.data)))
  17. print("t_reshape.data 内存地址:{}".format(id(t_reshape.data))) 
  20. tensor([2, 4, 3, 1, 5, 6, 7, 0])
  21. t:tensor([2, 4, 3, 1, 5, 6, 7, 0])
  22. t_reshape:
  23. tensor([[[2, 4],
  24.          [3, 1]],
  26.         [[5, 6],
  27.          [7, 0]]])
  28. t:tensor([1024,    4,    3,    1,    5,    6,    7,    0])
  29. t_reshape:
  30. tensor([[[1024,    4],
  31.          [   3,    1]],
  33.         [[   5,    6],
  34.          [   7,    0]]])
  35. t.data 内存地址:1556953167336
  36. t_reshape.data 内存地址:1556953167336


上面这两个是共内存的， 一个改变另一个也会改变。这个要注意一下。
torch.transpose(input, dim0, dim1): 交换张量的两个维度, 矩阵的转置常用， 在图像的预处理中常用， dim表示要交换的维度```json t = torch.rand((2, 3, 4))
print(t) t_transpose = torch.transpose(t, dim0=0, dim1=2)
print(“t shape:{}\nt_transpose shape: {}”.format(t.shape, t_transpose.shape))

tensor([[[0.7480, 0.5601, 0.1674, 0.3333], [0.4648, 0.6332, 0.7692, 0.2147], [0.7815, 0.8644, 0.6052, 0.3650]],

  1.     [[0.2536, 0.1642, 0.2833, 0.3858],
  2.      [0.8337, 0.6173, 0.3923, 0.1878],
  3.      [0.8375, 0.2109, 0.4282, 0.4974]]])

t shape:torch.Size([2, 3, 4]) t_transpose shape: torch.Size([4, 3, 2]) tensor([[[0.7480, 0.2536], [0.4648, 0.8337], [0.7815, 0.8375]],

  1.     [[0.5601, 0.1642],
  2.      [0.6332, 0.6173],
  3.      [0.8644, 0.2109]],
  5.     [[0.1674, 0.2833],
  6.      [0.7692, 0.3923],
  7.      [0.6052, 0.4282]],
  9.     [[0.3333, 0.3858],
  10.      [0.2147, 0.1878],
  11.      [0.3650, 0.4974]]])
  1. <br />torch.t(input): 2 维张量的转置， 对矩阵而言，相当于 torch.transpose(inpuot, 0,1)<br />torch.squeeze(input, dim=None, out=None): 压缩长度为 1 的维度， dim 若为 None，移除所有长度为 1 的轴，若指定维度，当且仅当该轴长度为 1 时可以被移除```json
  2. t = torch.rand((1, 2, 3, 1))
  3. t_sq = torch.squeeze(t)
  4. t_0 = torch.squeeze(t, dim=0)
  5. t_1 = torch.squeeze(t, dim=1)
  6. print(t.shape)        
  7. print(t_sq.shape)     
  8. print(t_0.shape)     
  9. print(t_1.shape)

torch.unsqueeze(input, dim, out=None): 依据 dim 扩展维度

张量的数学运算

标量运算

Pytorch 中提供了丰富的数学运算，可以分为三大类： 加减乘除， 对数指数幂函数，三角函数
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图16
这里重点演示一下加法这个函数， 因为这个函数有一个小细节：
torch.add(input, alpha=1, other, out=None): 逐元素计算 input+alpha * other。 注意人家这里有个 alpha，叫做乘项因子。类似权重的个东西。
这个东西让计算变得更加简洁， 比如线性回归我们知道有个 y = wx + b， 在这里直接一行代码 torch.add(b, w, x) 就搞定。 类似的还有两个方法：
torch.addcdiv(input, value=1, tensor1, tensor2, out=None):
这个实现了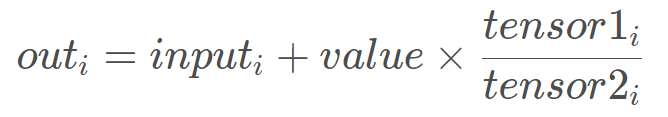image.png
torch.addcmul(input, value=1, tensor1, tensor2, out=None)
这个实现了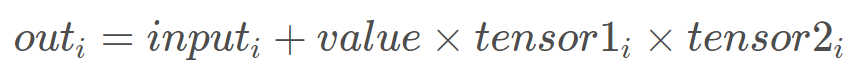image.png
这个在优化的时候经常会用到。

  1. t_0 = torch.randn((3, 3))
  2. t_1 = torch.ones_like(t_0)
  3. t_add = torch.add(t_0, 10, t_1)
  5. print("t_0:\n{}\nt_1:\n{}\nt_add_10:\n{}".format(t_0, t_1, t_add))
  8. t_0:
  9. tensor([[-0.4133,  1.4492, -0.1619],
  10.         [-0.4508,  1.2543,  0.2360],
  11.         [ 1.0054,  1.2767,  0.9953]])
  12. t_1:
  13. tensor([[1., 1., 1.],
  14.         [1., 1., 1.],
  15.         [1., 1., 1.]])
  16. t_add_10:
  17. tensor([[ 9.5867, 11.4492,  9.8381],
  18.         [ 9.5492, 11.2543, 10.2360],
  19.         [11.0054, 11.2767, 10.9953]])

向量运算

向量运算符只在一个特定轴上运算，将一个向量映射到一个标量或者另外一个向量。

  1. a = torch.arange(1,10).float()
  2. print(torch.sum(a))
  3. print(torch.mean(a))
  4. print(torch.max(a))
  5. print(torch.min(a))
  6. print(torch.prod(a)) 
  7. print(torch.std(a))  
  8. print(torch.var(a))  
  9. print(torch.median(a))

cum 累积

  1. a = torch.arange(1,10)
  3. print(torch.cumsum(a,0))    
  4. print(torch.cumprod(a,0))    
  5. print(torch.cummax(a,0).values)
  6. print(torch.cummax(a,0).indices)
  7. print(torch.cummin(a,0))

张量排序

  1. a = torch.tensor([[9,7,8],[1,3,2],[5,6,4]]).float()
  2. print(torch.topk(a,2,dim = 0),"\n")
  3. print(torch.topk(a,2,dim = 1),"\n")
  4. print(torch.sort(a,dim = 1),"\n")

矩阵运算

矩阵必须是二维的。类似 torch.tensor([1,2,3]) 这样的不是矩阵。
矩阵运算包括：矩阵乘法，矩阵转置，矩阵逆，矩阵求迹，矩阵范数，矩阵行列式，矩阵求特征值，矩阵分解等运算。

  1. 矩阵乘法json a = torch.tensor([[1,2],[3,4]]) b = torch.tensor([[2,0],[0,2]]) print(a@b)

  2. 转置json a = torch.tensor([[1.0,2],[3,4]]) print(a.t())

  3. 矩阵求逆json a = torch.tensor([[1.0,2],[3,4]]) print(torch.inverse(a))

  4. 矩阵求迹json a = torch.tensor([[1.0,2],[3,4]]) print(torch.trace(a))

  5. 求范数和行列式```json a = torch.tensor([[1.0,2],[3,4]]) print(torch.norm(a))

a = torch.tensor([[1.0,2],[3,4]]) print(torch.det(a))

  2. 6. 特征值和特征向量```json
  3. a = torch.tensor([[1.0,2],[-5,4]],dtype = torch.float)
  4. print(torch.eig(a,eigenvectors=True))

  1. QR 分解json a = torch.tensor([[1.0,2.0],[3.0,4.0]]) q,r = torch.qr(a) print(q,"\n") print(r,"\n") print(q@r)

  2. SVD 分解```json a=torch.tensor([[1.0,2.0],[3.0,4.0],[5.0,6.0]])

u,s,v = torch.svd(a)

print(u,”\n”) print(s,”\n”) print(v,”\n”)

print(u@torch.diag(s)@v.t())

  2. <a name="661f60dc"></a>
  3. ## 搭建一个线性回归模型
  4. 线性回归是分析一个变量与另外一 (多) 个变量之间关系的方法。 因变量是 y， 自变量是 x， 关系线性： <br />y = wx + b<br />任务就是求解 w，b。<br />我们的求解步骤：
  6. 1. 确定模型： Model -> y = wx + b
  7. 1. 选择损失函数： 这里用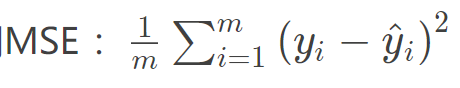
  9.     ![image.png](https://cdn.nlark.com/yuque/0/2020/png/750176/1600336646268-0bcb7281-6f70-4817-afcf-c132257cd382.png#align=left&display=inline&height=44&margin=%5Bobject%20Object%5D&name=image.png&originHeight=88&originWidth=460&size=7498&status=done&style=none&width=230)
  11. 3. 求解梯度并更新 w, b<br />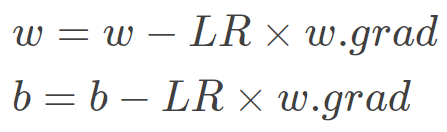
  13. ![image.png](https://cdn.nlark.com/yuque/0/2020/png/750176/1600336665176-60ac8077-45ac-490e-ac2f-87ff306fbc83.png#align=left&display=inline&height=66&margin=%5Bobject%20Object%5D&name=image.png&originHeight=132&originWidth=447&size=11041&status=done&style=none&width=223.5)<br />这就是我上面说的叫做代码逻辑的一种思路， 写代码往往习惯先有一个这样的一种思路，然后再去写代码的时候，就比较容易了。 而如果不系统的学一遍 Pytorch， 一上来直接上那种复杂的 CNN， LSTM 这种，往往这些代码逻辑不好形成，因为好多细节我们根本就不知道。 所以这次学习先从最简单的线性回归开始，然后慢慢的到复杂的那种网络。下面我们开始写一个线性回归模型：
  14. ```json
  15. x = torch.rand(20, 1) * 10
  16. y = 2 * x + (5 + torch.randn(20, 1))
  19. w = torch.randn((1), requires_grad=True)
  20. b = torch.zeros((1), requires_grad=True)   
  22. for iteration in range(100):
  24.     wx = torch.mul(w, x)
  25.     y_pred = torch.add(wx, b)
  28.     loss = (0.5 * (y-y_pred)**2).mean()
  31.     loss.backward()
  34.     b.data.sub_(lr * b.grad)    
  35.     w.data.sub_(lr * w.grad)
  38.     w.grad.data.zero_()
  39.     b.grad.data.zero_()
  41. print(w.data, b.data)

我们看一下结果：

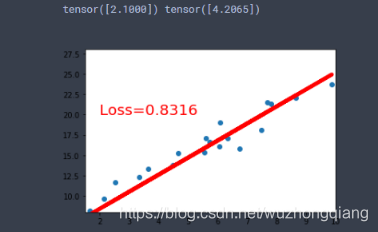
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图19

5. 总结

今天的学习内容结束， 下面简单的梳理一遍，其实小东西还是挺多的， 首先我们从 Pytorch 最基本的数据结构开始，认识了张量到底是个什么东西，说白了就是个多维数组，然后张量本身有很多的属性， 有关于数据本身的 data, dtype, shape, dtype, 也有关于求导的 requires_grad, grad, grad_fn, is_leaf。 然后学习了张量的创建方法， 比如直接创建，从数组创建，数值创建，按照概率创建等。 这里面涉及到了很多的创建函数 tensor(), from_numpy(), ones(), zeros(), eye(), full(), arange(), linspace(), normal(), randn(), rand(), randint(), randperm() 等等吧。
接着就是张量的操作部分， 有基本操作和数学运算， 基本操作部分有张量的拼接两个函数 (.cat, .stack), 张量的切分两个函数 (.chunk, .split), 张量的转置 (.reshape, .transpose, .t)， 张量的索引两个函数 (.index_select, .masked_select)。 数学运算部分，也是很多数学函数，有加减乘除的，指数底数幂函数的，三角函数的很多。
最后基于上面的所学完成了一个简单的线性回归。 下面以一张思维导图把这一篇文章的内容拎起来：
系统学习Pytorch笔记一：Pytorch的数据载体张量与线性回归 - 图20