梯度下降

一维梯度下降

证明：沿梯度反方向移动自变量可以减小函数值
泰勒展开：
f(x+ϵ)=f(x)+ϵf′(x)+O(ϵ2)
代入沿梯度方向的移动量 ηf′(x)：
f(x−ηf′(x))=f(x)−ηf′2(x)+O(η2f′2(x))
f(x−ηf′(x))≲f(x)
x←x−ηf′(x)

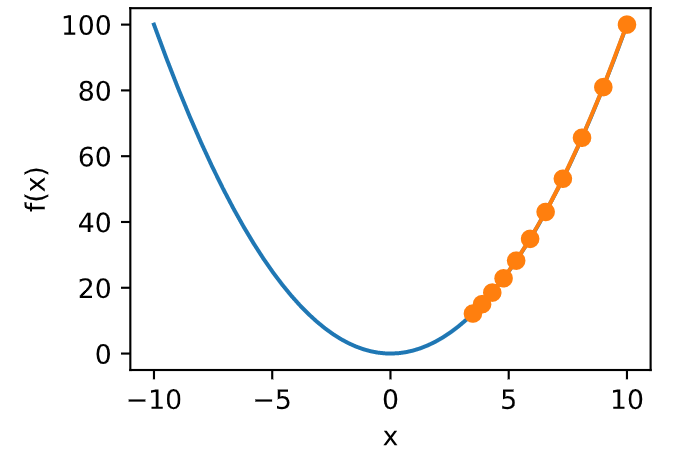
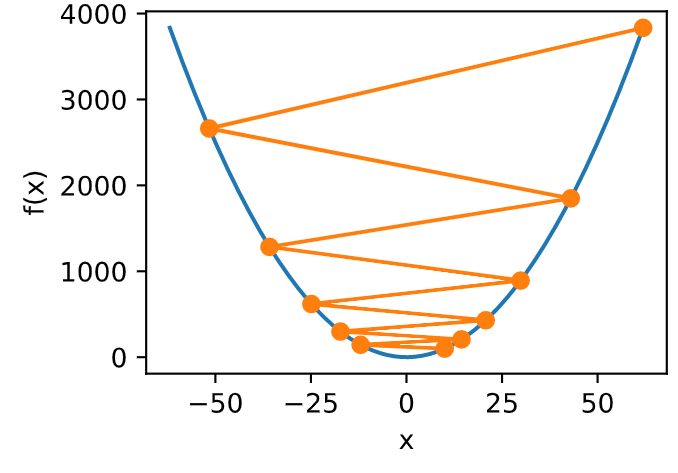
学习率

  • 0.05
    • image.png

  • 1.1

    • image.png

      局部极小值

      image.png

      多维梯度下降

      ∇f(x)=[∂f(x)∂x1,∂f(x)∂x2,…,∂f(x)∂xd]⊤
      f(x+ϵ)=f(x)+ϵ⊤∇f(x)+O(‖ϵ‖2)
      x←x−η∇f(x)

      自适应方法

      牛顿法

      在 x+ϵ 处泰勒展开：
      f(x+ϵ)=f(x)+ϵ⊤∇f(x)+12ϵ⊤∇∇⊤f(x)ϵ+O(‖ϵ‖3)
      最小值点处满足: ∇f(x)=0, 即我们希望 ∇f(x+ϵ)=0, 对上式关于 ϵ 求导，忽略高阶无穷小，有：
      ∇f(x)+Hfϵ=0 and hence ϵ=−Hf−1∇f(x)

  • 引入了二阶导的信息，收敛速度快

    收敛性分析

    只考虑在函数为凸函数, 且最小值点上 f″(x∗)>0 时的收敛速度：
    令 xk 为第 k 次迭代后 x 的值， ek:=xk−x∗ 表示 xk 到最小值点 x∗ 的距离，由 f′(x∗)=0:
    0=f′(xk−ek)=f′(xk)−ekf′′(xk)+12ek2f′′′(ξk)for some ξk∈[xk−ek,xk]
    两边除以 f″(xk), 有：
    ek−f′(xk)/f′′(xk)=12ek2f′′′(ξk)/f′′(xk)
    代入更新方程 xk+1=xk−f′(xk)/f′′(xk), 得到：
    xk−x∗−f′(xk)/f′′(xk)=12ek2f′′′(ξk)/f′′(xk)
    xk+1−x∗=ek+1=12ek2f′′′(ξk)/f′′(xk)
    当 12f′′′(ξk)/f′′(xk)≤c 时，有:
    ek+1≤cek2

    预处理 （Heissan阵辅助梯度下降）

    x←x−ηdiag⁡(Hf)−1∇x

  • 使得不同维度的下降幅度和它当前的数值是大致成比例的

    随机梯度下降

    随机梯度下降参数更新

    对于有 n 个样本对训练数据集，设 fi(x) 是第 i 个样本的损失函数, 则目标函数为:
    f(x)=1n∑i=1nfi(x)
    其梯度为:
    ∇f(x)=1n∑i=1n∇fi(x)
    使用该梯度的一次更新的时间复杂度为 O(n)
    随机梯度下降更新公式 O(1):
    x←x−η∇fi(x)
    且有：
    Ei∇fi(x)=1n∑i=1n∇fi(x)=∇f(x)

    动态学习率

    梯度下降 - 图4

  • 一开始学习率要大，尽快收敛

  • 随着优化的深入，学习率逐渐减小，避免震荡

    小批量随机梯度下降

  • batch介于1和total之间

  • batch过小，没有很好地利用并行性，引入噪声
  • batch过大，更新一次的计算复杂度高，更新慢，噪声最小