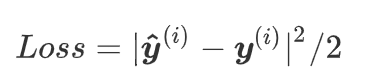本节讨论的是分类任务
Softmax的基本概念
直接使用线性输出层有两个问题:
- 输出层的输出值的范围不确定，我们难以直观上判断这些值的意义
- 由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量
softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布：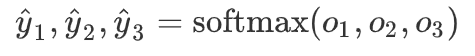
其中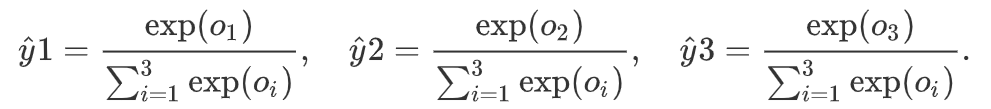
它将
转换成了一个概率分布，并且不改变预测类别输出
交叉熵损失函数
- 平方损失估计
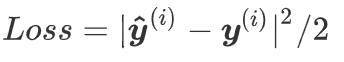在分类任务中过于严格了 - 改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数，常用的就是交叉熵
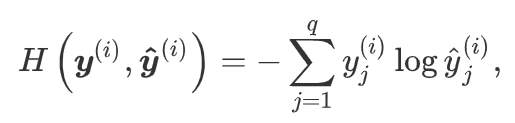
- 交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时，我们并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。
- 如果每个样本只有一个标签，那么交叉熵损失可以简写成
- 我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。
- 准确率（accuracy）：正确预测数量与总预测数量之比。
若有收获，就点个赞吧
0 人点赞
