题目
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。
要求不能创建任何新的结点，只能调整树中结点指针的指向。
注意：
需要返回双向链表最左侧的节点。
例如，输入下图中左边的二叉搜索树，则输出右边的排序双向链表。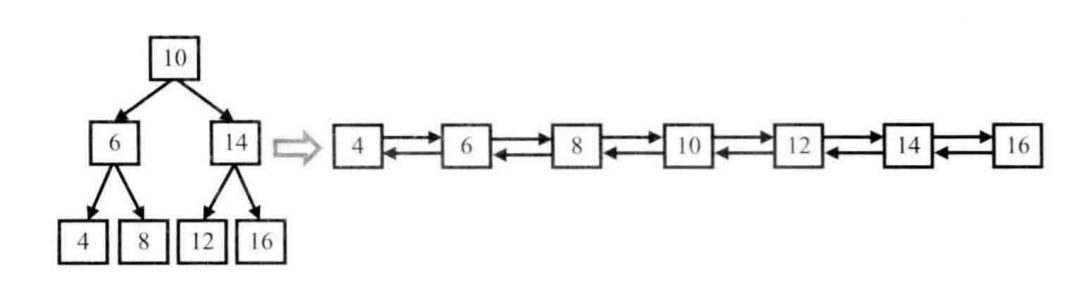

解法一：后序遍历

先获取左子树最右结点和右子树最左结点，然后进行拼接
时间复杂度O(n)，空间复杂度O(1)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* convert(TreeNode* root) {
        if (!root) return nullptr;
        auto ans = dfs(root);
        return ans.first;
    }
    pair<TreeNode*, TreeNode*> dfs(TreeNode* u) {
        if (!u->left && !u->right) return {u, u};
        else if (u->left && u->right) {
            auto l = dfs(u->left), r = dfs(u->right);
            l.second->right = u, u->left = l.second;
            u->right = r.first, r.first->left = u;
            return {l.first, r.second};
        }
        else if (u->left) {
            auto l = dfs(u->left);
            l.second->right = u, u->left = l.second;
            return {l.first, u};
        }
        else {
            auto r = dfs(u->right);
            u->right = r.first, r.first->left = u;
            return {u, r.second};
        }
    }
};

解法二：逆中序遍历

从大往小遍历与拼接，用一个指针维护当前值最小的结点，遍历结束后，该指针即为二叉链表起点
时间复杂度O(n)，空间复杂度O(1)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* convert(TreeNode* root) {
        if (!root) return nullptr;
        TreeNode *last = nullptr;
        dfs(root, last);
        return last;
    }
    void dfs(TreeNode* u, TreeNode* &f) {
        if (!u) return;
        if (u->right) dfs(u->right, f);
        u->right = f;
        if (f) f->left = u;
        f = u;
        if (u->left) dfs(u->left, f);
    }
};