插入排序：
    插入排序顾名思义，就是在排序的过程中，把数组的每一个元素按照大小关系，插入到前面有序区的对应位置。
    例如： 数组 [5, 8, 6, 3, 9, 2, 1, 7]，共有n个元素，则需要n-1趟。 见下表每趟的排序结果。

    排序算法 - 插入排序，希尔排序，折半查找 - 图1

    插入排序的代码示例：

    1. function insertSort(arr){
    2.     var length = arr.length;
    3.     // gap取1
    4.     var gap = 1;
    6.     for (var i = 1; i < length; i++) {
    7.       for (var j = (i-gap); j >= 0, arr[j] > arr[j+gap]; j-=gap) {
    8.         var temp = arr[j];
    9.         arr[j] = arr[j+gap];
    10.         arr[j+gap] = temp;
    11.       }
    12.     }
    14.     return arr;
    15. }
    17. var arr1 = [8, 5, 6, 3, 9, 2, 1, 7];
    18. insertSort(arr1);
    19. console.log(arr1);

    插入排序的平均时间复杂度是O（n^2）。这个排序算法并不复杂，但显然并不是一个高效的排序算法。

    那么，怎样可以对插入排序算法做出优化呢？我们不妨从插入排序的两个特点入手：

    1. 在大多数元素已经有序的情况下，插入排序的工作量较小；

    这个结论很明显，如果一个数组大部分元素都有序，那么数组中的元素自然不需要频繁地进行比较和交换。

    1. 在元素数量较少的情况下，插入排序的工作量较小；

    这个结论更加显而易见，插入排序的工作量和n的平方成正比，如果n比较小，那么排序的工作量自然要小得多。

    希尔排序是对插入排序的一种优化：

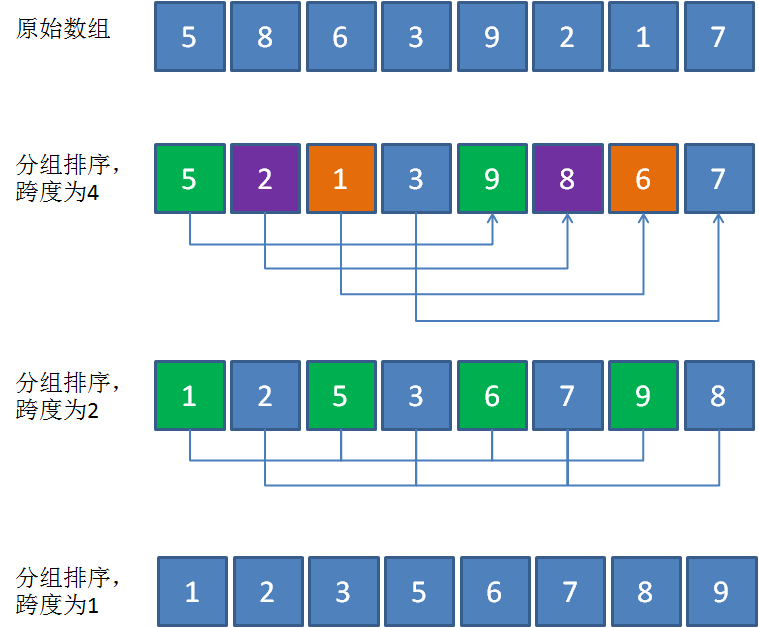
    排序算法 - 插入排序，希尔排序，折半查找 - 图2

    逐步分组进行粗调，再进行直接插入排序的思想，就是希尔排序，根据该算法的发明者，计算机科学家Donald Shell的名字所命名。

    希尔排序是稳定排序吗？
    不是一个稳定排序算法，值相同的元素可能会被调换位置。

    希尔排序的gap步长为1时，这时候其实就是简单插入排序了。

    希尔排序代码：

    1. function shellSort(arr){
    2.     var length = arr.length;
    3.     //向上取整获得步长，也可以向下取整
    4.     var gap = Math.floor(length/2);
    6.     //增加学习性，添加了趟数
    7.     var times = 1;
    9.     for(; gap > 0; gap = Math.floor(gap/2), times++) {
    10.       for (var i = gap; i < length; i++) {
    11.         // j-=gap 很重要，是回退操作
    12.         for (var j = (i-gap); j >= 0, arr[j] > arr[j+gap]; j-=gap) {
    13.           var temp = arr[j];
    14.           arr[j] = arr[j+gap];
    15.           arr[j+gap] = temp;
    16.         }
    17.       }
    19.       console.log('第' + times + '趟', arr);
    20.     }
    23.     return arr;
    24. }
    26. var arr1 = [5, 8, 6, 3, 9, 2, 1, 7];
    27. shellSort(arr1);
    29. // 第一趟(gap=4)：5 2 1 3 9 8 6 7
    30. // 第二趟(gap=2)：1 2 5 3 6 7 9 8
    31. // 第三趟(gap=1)：1 2 3 5 6 7 8 9

    折半查找：
    折半查找的前提是待查找序列是一个有序序列。

    1. var array1 = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21];
    2. var index = mySearch(array1, 19);
    3. console.log(array1[index]);
    5. function mySearch(array1, value){
    6.   var low = 0;
    7.   var high = array1.length - 1;
    9.   while(low < high) {
    10.     var mid = Math.floor((low + high)/2);
    11.     console.log(low, mid, high);
    13.     if (array1[mid] < value) {
    14.       low = mid + 1;
    15.     }
    16.     else {
    17.       // 等于的情况包含在这个分支里，所以返回high
    18.       high = mid;
    19.     }
    20.   }
    22.   return high;
    23. }
    1.    有序的顺序表的话，由折半查找法的定义本身，每次比较之后问题规模都会减小一半，当pow(2, k)恰好等于N时，查找规模可以说已经是0了，所以折半查找的最大比较次数应当是floor(k) + 1,其中k满足2^k=N。<br />其中对于任意二分查找，其比较次数都在[1, floor(k)+1]之间，当N=1000时，最大比较次数为11。