算法动画了解
时间复杂度
算法时间复杂度是衡量一个算法优劣的主要因素。
运行时间的增长率
再例如冒泡排序的时间复杂度是N*N;快排的时间复杂度是log(n)。
其实目的只有一个就是把衡量算法时间的关于输入规模的函数f(n)用另一个关于输入规模的函数集来表示

比如:
要找到一个数组里面最大的一个数,你要把n个变量都扫描一遍,操作次数为n,那么算法复杂度是O(n).
用冒泡排序排一个数组,对于n个变量的数组,需要交换变量位置次,那么算法复杂度就是O(n^2).
有时候,如果对变量操作的次数是个多项式比如, 就取数量级最大的那个,O()
Big O. https://zh.wikipedia.org/wiki/大O符号
《算法导论》
Big 0
大O符号(英语:Big O notation),又称为渐进符号,是用于描述函数渐近行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。
渐近上界: 最坏的情况
所以当我们说“时间复杂度为O(n²)时”,也就是说最坏情况下时间复杂度为O(n²)。
有一些常见的增长快慢的函数:
指数量级: 2n,n!
多项式量级: n,n{1⁄2}
对数多项式量级: logn,log^2 n,loglogn
算法的好坏,叫做效率。
O(n)是线性的,比如我有一个数据结构是队列,里面有n个元素,我从头到尾遍历一遍,复杂度就是O(n).O( )是二次方的,比如冒泡算法就是典型的,需要在一个线性数据结构上进行二重循环的操作。通常我们对算法的追求O(logN)或者O(1),但这两种时间复杂度是可遇不可求的。
O(logN)一般的要求是二分法,应用在顺序的数据结构上。至于O(1),如果输入的量级和输出完全无关,那么他就是常数级别的时间复杂度,这是理论上最好的时间复杂度。
渐进记号
渐进确界 渐进上界(最坏情况) 渐进下界(最好情况)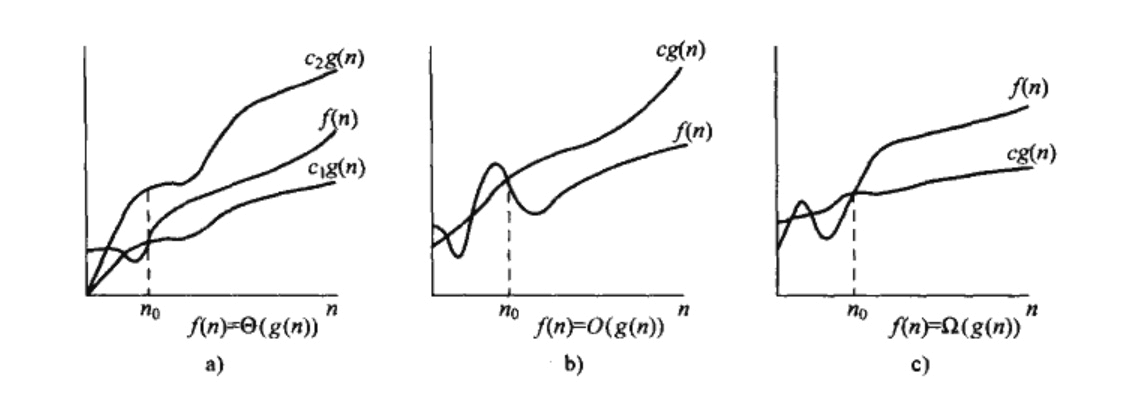
通俗解释
有100个人站在你面前,脸盲的你得两两结对、一对一对观察,才能找到唯一的一对双胞胎。同上,我总是可以把双胞胎放在你最后找到的一对。你至多一共要观察4 950对。如果换成10 000个,那就是49 995 000对,也就是10 100倍的工作量这就是O(n²)
有128个人站在你面前,你要把他们按照高矮排序——我们假设用归并排序——你先把他们分成两个64人的大队,每个大队分成两个32人的中队,每个中队分成……直到最后每一个“小小…小队”只剩一个人。显然,一个人一定是已经排好序的。然后反向操作,将刚刚拆分的队伍合并起来。合并队伍的时候,由于已经排好序,只需要取出两队排头进行比较,就找到了最矮的一个,取出来——如此进行下去,合成的两倍大的队伍也将是有序的。显然,这个合并操作,是O(n)的。总共的比较次数,不会超过两个队伍的总人数。最后的问题只是,有多少次“分割-合并”操作。每次分割数量都减半,很明显是7(log 128)次。由此看来,大致需要执行7×128次操作。这就是O(nlogn)。
排序算法
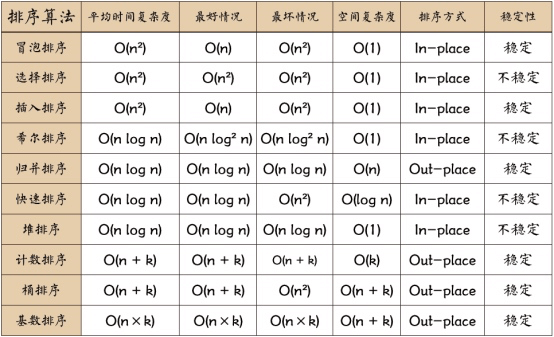
排序在前端的实现
Array.prototype.sort
目前大部分浏览器通过使用归并排序和快排来实现sort方法
快排
- 先从数列中去除一个数作为“基准”(理论上可以随便选取一个数)
- 实现数组分区:将比这个”基准数“大的数放到“基准”的右边,小于或等于“基准数”的数放到“基准”的左边;
- 再对左右区间重复第二步,直到各区间只有一个数
反转单向链表
树的遍历
字符串相关
字符串相关算法中,Trie 树可以解决解决很多问题,同时具备良好的空间和时间复杂度,比如以下问题
词频统计
前缀匹配

