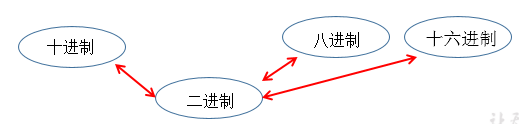
1.编程中涉及的进制及表示方式：

2.二进制的使用说明：

• 2.1 计算机底层的存储方式：所有数字在计算机底层都以二进制形式存在。
• 2.2 二进制数据的存储方式：所有的数值，不管正负，底层都以__补码的方式存储。
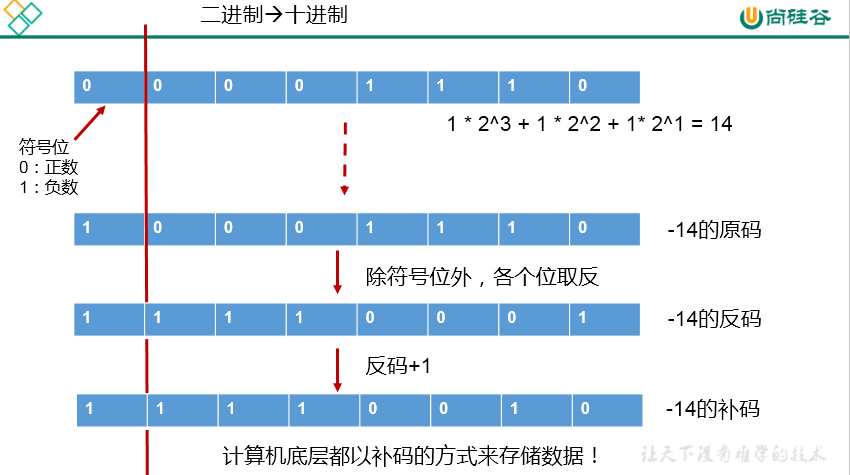
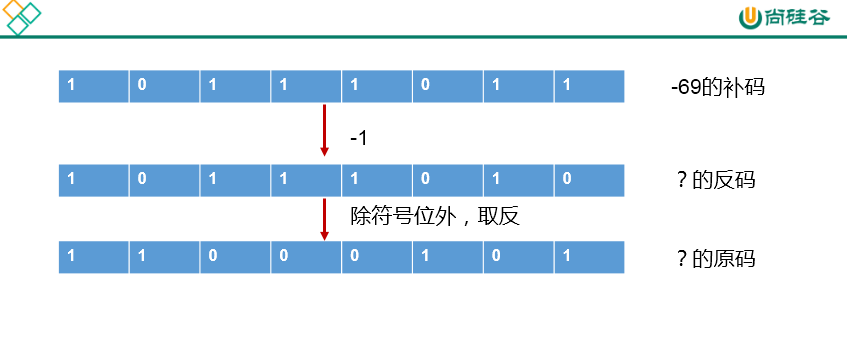
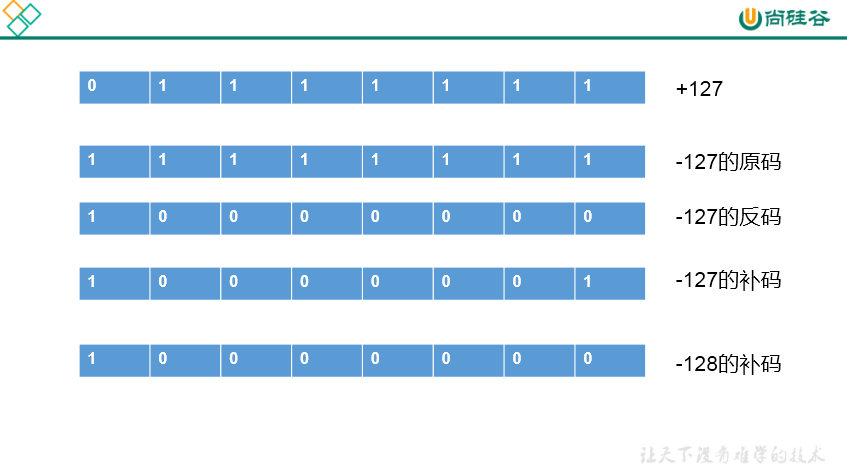
• 2.3 原码、反码、补码的说明：
  • 正数：三码合一
  • 负数：
    • 

3.进制间的转换：

3.1 图示：

3.2 图示二进制转换为十进制：

3.3 图示十进制转换为二进制：

3.4 二进制与八进制、十六进制间的转换：

4. 数制，进制转换

1）. 将任意进制数转换为等值的十进制数

解题方法和步骤：
利用公式
即可将任何进制的数转换为等值的十进制数。上式中的N为以十进制数表示的计数进位的基数，为第位的系数，它可以是0 ~ N中的任何一个整数。若整数部分有n位，小数部分有m位，则t 将包含从n-1到0的所有正整数和从－1到－m的所有负整数。
对于整数部分为n位、小数部分为m位的二进制数(N=2) ，则得到等值的十进制数为

其中每一位的系数，可能是1或0。

对于整数部分为n位、小数部分为m位的八进制数(N=8) ，则得到等值的十进制数为

其中每一位的系数，可能是0~7当中的某个数值。

对于整数部分为n位、小数部分为m位的十六进制数(N=16) ，则得到等值的十进制数为

式中每一位的系数，的取值可能是0~15当中的某一数值。

2）. 将十进制数转换为等值的二进制数

解题方法和步骤：
若十进制数包含整数和小数，则整数部分和小数部分需按不同方法分别进行转换。
(1) 整数部分的转换 (倒取)
将十进制数除以2，所得余数即二进制数的;
将上面得到的商再除以2，所得余数即二进制数的;
将上面得到的商再除以2，所得余数即二进制数的;
依此类推，直到所得商等于0为止，就得到了等值的二进制数。
(2) 小数部分的转换（顺取）
将十进制数的小数乘以2，所得乘积的整数部分即;
将上面得到的乘积的小数部分再乘以2，所得乘积的整数部分即;
将上面得到的乘积的小数部分再乘以2，所得乘积的整数部分即;
依此类推，直到求出要求的位数为止，就得到了等值的二进制数。

3）. 二进制与八进制和十六进制间的互相转换

解题方法和步骤：
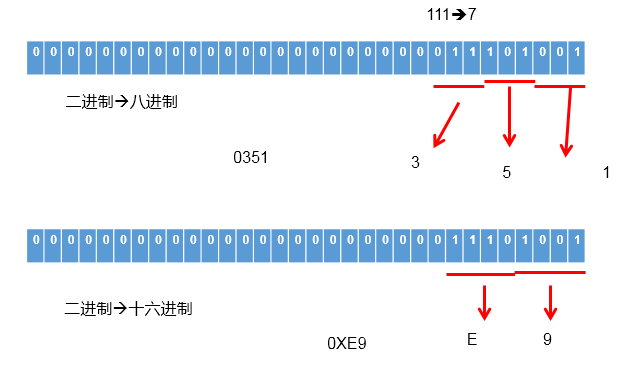
在将二进制数转换为八进制数时，首先将二进制数的整数部分从最低位向高位每3位划分为一组，同时将二进制数的小数部分从最高位向低位每3位划分为一组，然后将每一组代之以等值的八进制数，就得到了所求的转换结果。
在将二进制数转换为十六进制数时，首先将二进制数的整数部分从最低位向高位每4位划分为一组，同时将二进制数的小数部分从最高位向低位每4位划分为一组，然后将每一组代之以等值的十六进制数，就得到了所求的转换结果。
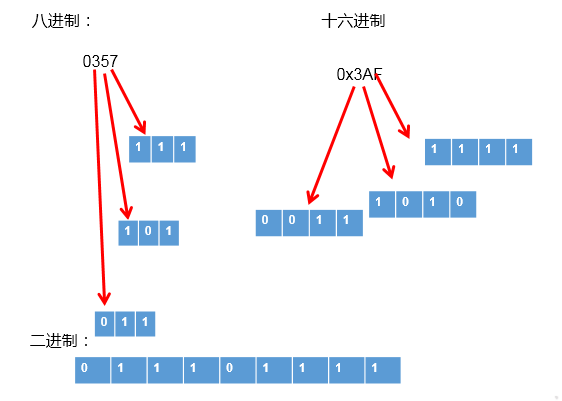
相反地，在将八进制数转换为二进制数时，只需将八进制数的每一位代之以等值的3位二进制数并按原来的顺序排列起来就行了。
同理，在将十六进制数转换为二进制数时，只需将十六进制数的每一位代之以等值的4位二进制数并按原来的顺序排列起来就行了。

4）. 将十进制数转换为等值的八进制和十六进制数

转换方法和步骤：
(1) 首先将十进制数转换为等值的二进制数。
(2) 再将得到的二进制数转换为等值的八进制和十六进制数。