一个SLAM系统分为前端和后端，其中前端也称为视觉里程计（Visual Odometry，VO）。视觉里程计根据相邻图像的信息估计出粗略的相机运动，给后端提供较好的初始值。视觉里程计主要分为两个大类：① 特征点法；② 直接法。

视觉里程计的核心问题是如何根据图像估计相机运动。

特征点

特征点是图像里一些特别的地方。比如图像中的角点、边缘和区块。角点的提取算法有很多，比如Harris角点、FAST角点、GFTT角点，这些都是2000年以前的算法。角点在相机移动后可能就提取不出来了，为此需要提取更加稳定的局部图像特征，比如SIFT、SURF、ORB等等。这些人工设计（通过特定算法）的特征点能够拥有如下性质：① 可重复性（相同的特征可以在不同的图像中找到）；② 可区别性（不同的特征有不同的表达）；③ 高效率（特征点的数量远小于像素的数量）；④ 本地性（特征仅与一小片图像区域相关）。

特征点的组成：关键点（KeyPoint）和描述子（Descriptor）。关键点是该特征点在图像中的位置，有些特征点还具有朝向、大小等信息。描述子是按照“外观相似的特征应该有相似的描述子”的原则设计的。

1.1 ORB特征（Oriented FAST and Rotated BRIEF）（重点）

特征点提取方法有很多，但ORB提取算法在实时性上优势很大，并且精度也不低。

ORB特征：由关键点和描述子组成。提取ORB特征分为两个步骤：

1. FAST角点提取：在原始FAST角点提取算法的基础上，计算了特征点区域的质心M，得到特征点的主方向OM
2. BRIEF描述子：对前一步提取的特征点的周围区域进行描述。

相对于之前的FAST算法：

• ORB通过构建图像金字塔来实现尺度不变性，在金字塔的每一层进行角点检测。比如相机在后退，那么我们应该能够在上一个图像金字塔的上层（像素低、远）和下一个图像金字塔的下层（像素高、近）找到匹配。ORB通过
• ORB通过灰度质心法（Intensity Centroid）实现旋转不变性。

这里的XX不变性可以理解为尺度缩放（图像旋转）后依然能在第二张图像中找到对应的特征点匹配。

1.1.1 Fast关键点（oriented）

流程：

1. 选取像素p，假设它的亮度为lp
2. 设一个阈值T，比如lp的20%
3. 以像素点为中心，选取半径为3的圆上面的16个像素点（不是圆内）
4. 假如选取的圆上，有连续的N个点亮度大于lp+T或者lp-T，那么像素p可以被认为是特征点
5. 循环以上4步，对每一个像素执行相同操作

灰度质心法提取质心：

1. 定义图像的矩（图像矩是图像像素强度的某个特定加权平均，用来描述图像特征，有原点矩，中心矩，hu矩）
2. 根据原点矩的一阶矩和零阶矩的比值可以找到图像块的质心（零阶矩是区域内所有像素的灰度值综合，一阶矩是单个方向上）

这里的灰度质心法是在圆形区域内进行的灰度质心计算，ORBSLAM是先旋转坐标再从图像中采点提取，并不是先取再旋转，所以如果用正方形，旋转前后会取到不同部分的像素。

1.1.2 BRIEF描述子（Binary Robust Independent Elementary Features）

BRIEF描述子（descriptor）是一种二进制描述子，其描述向量由许多个0和1组成，这里的0和1编码了关键点附近两个随机像素（比如p和q）的大小关系：如果p比q大，则取1，反之就取0。如果我们取了128个这样的p、q，则最后得到128维的二进制向量。
通俗的理解：在关键点p的周围以一定的模式选取N个点对，把这N个点对的结果组合起来作为描述子。

由于ORB特征在提取角点是提供的方向信息，所以计算旋转之后的steer BRIEF特征使得ORB的描述子具有较好的旋转不变性。

特征匹配

特征匹配就是将图像1和图像2提取的特征点进行相互对应。特征匹配是视觉SLAM中极为关键的一步，宽泛的说，特征匹配解决了SLAM中的数据关联问题（data association）。匹配方式是计算描述子之间的距离，然后排序，取距离最近（特征最相似）的一个作为匹配点。对于二进制描述子，常用汉明距离（不同位数的个数）。对于浮点数描述子，常用欧氏距离。

特征匹配方法：

• 暴力匹配法，将图1中的m个特征点和图2中的n个特征点进行m*n次匹配
• 快速近邻最近邻（FLANN）：适合于匹配点数量极多的情况

特征匹配方法大多已集成进OpenCV中。

计算相机运动

有了匹配好的点对后，就可以估计相机的运动：

1. 当相机为单目时，使用对极几何解决。根据两组2D点估计运动
2. 如果一组为3D、一组为2D时（或者单目用对极几何计算出初始化深度），使用PnP求解
3. 如果相机为双目、RGB-D是，使用ICP求解。利用两组3D点估计运动

2. 2D-2D对极几何

2.1 对极约束

两个图像I1、I2，两相机中心O1、O2，两个图像中的对应特征点p1、p2，空间点P（相机坐标系）。O1O2P组成的平面为极平面（Epipolar plane），极平面与I1和I2相交形成的线为极线（Epipolar line），O1O2为基线，基线和I1、I2相交的点称为极点（Epipoles）。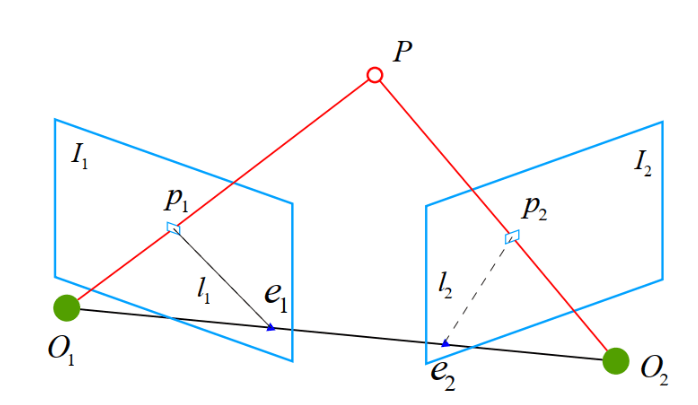

2.2 对极约束式子的引出

目的：我们希望用一个式子将已知的空间信息（特征点位置等）和相机运动（R, t）约束起来，以求解相机的运动R和t。p1和p2之间的转换关系。

推导：我们知道像素坐标系和相机坐标系的转换关系：

Z为点的深度，换一种方式书写：

在使用其次坐标时，一个向量将等于它自身乘上任意的非零常数。这通常表示一种投影关系，比如p1和s1p1成投影关系，它们在齐次坐标系下的意义是相等的。我们称这种相等关系为尺度意义下相等（equal to scale），记为：

于是，我们用x1和x2来表示两个像素点p1p2的归一化平面上的坐标，有：

而x1 x2仍然具有尺度意义下相等关系：

两边同时左乘，再同时左乘：

回忆反对称矩阵的性质反对称矩阵的性质，相当于叉积，得到了与x2垂直的向量，再和x2进行內积结果为0.则我们可以吧\simeq写为等号，于是就得到了对极约束：

对极约束的几何意义：三者共面。

其中的部分记作两个矩阵：基础矩阵（Fundamental Matrix）F和本质矩阵（Essential Matrix）E：

由于对极约束，相机位姿估计问题变成以下两步：

1. 根据配对点的像素位置求出基础矩阵F或者本质矩阵E
2. 根据F或者E求出R, t

2.3 本质矩阵E

关于本质矩阵E的内在性质的证明：证明过程

2.4 单应矩阵

单应矩阵homography（H），描述了两个平面之间的映射关系。
流程：

1. 点p2与P的转换关系（内参外参）
2. 平面方程构建，构建左边=1
3. 代入转换关系方程
4. 把P提取出来
5. 把p1和P的转换关系代入
6. 得到p1和p2的关系式，