考虑放在机器人上的SLAM，那么我们会希望地图能够用于定位、导航、避障和交互，特征点地图显然不能满足所有的需求。关于地图的用处，大致归纳如下：

1. 定位。保存的地图允许机器人只对地图进行一次建模，并在其中定位，而不是每次启动都要做一次完整的SLAM。
2. 导航。导航是指机器人能够在地图中进行路径规划。我们至少得知道地图中哪些地方不可通过，而哪些地方是可以通过的。这要求地图是一种稠密的地图。
3. 避障。同上
4. 重建。
5. 交互。增强现实

稀疏地图只建模感兴趣的部分，也就是前面说了很久的特征点（路标点），而稠密地图是指建模所有看到过的部分。

1. 单目稠密重建

获取像素点的距离（深度），大概有以下方案：

1. 使用单目相机，估计相机运动，并用三角化计算像素的距离
2. 双目，利用左右相机的视差计算像素的距离
3. RGB-D相机直接获取像素距离

前两种称为立体视觉（stereo vision），其中移动弹幕相机的又称为移动视角的立体视觉。

在稠密深度图估计中，（稀疏建图使用的是特征点，而非每个像素），我们无法把每个像素都当做特征点计算描述子，因此，在稠密深度估计问题中，匹配就成为了重要的一环：如何确定第一幅图的某像素出现在其他图里的位置，这里运用到了极线搜索和块匹配技术。
当我们知道了某个像素在各个图中的位置，就能想特征点那样，利用三角测量取确定它们的深度。不过不同的是，这里要使用很多次三角测量法让深度估计收敛。我们希望深度估计能够随着测量的增加从一个非常不确定的值，逐渐收敛到一个稳定值，这就是深度滤波器技术。

1.1 极线搜索

简单理解：在视角1中，对于某个像素点，我们能够得到从相机光心与像素点连接形成的射线，称为O1P1，当我们知道相机的运动RT，那我们就知道视角2中，这条射线在图片中的投影线，这条线就是点P可能出现的位置，也称为极线。现在我们要在极线上找到对应像素点的位置。由于这里不是特征点匹配法，所以直觉上我们只能用像素的亮度值来匹配，这显然不合理。所以我们使用块匹配。我们在p1周围取一个ww方块，然后在极线上也取同样大小的方块，进行方块之间的相似性对比，这样就*从像素的灰度不变性变成了图像块的灰度不变性，这样显然更加合理。

相似性度量的计算方法有好几种：SAD（作差后求绝对值之和），SSD（作差后平法和），NCC（归一化互相关）

在搜索距离较长的情况下，通常会得到一个非凸函数：即结果很可能是极小值。这种情况下，我们会倾向于用概率分布来描述深度值，而非用一个单一的数值来描述深度。这样我们的问题就转到了在不断对不同图像进行极线搜索时，我们估计的深度分布将发生怎样的变化——这就是所谓的深度滤波器。

1.1.1 高斯分布的深度滤波器

在SLAM这种对实时性要求较强的场合，考虑到前端已经使用了不少计算量，建图方面则通常采用计算量较少的滤波器方式。

简单理解：

视角1-2中，像素的深度符合高斯分布 视角2-3中，像素的深度符合高斯分布 该像素对应点的高斯分布是前面两个分布的乘积。

现有一个问题是如何确定像素的深度分布。（看书上的公式推导）
综上，我们给出了估计稠密深度的一个完整过程：

1. 假设所有像素的深度满足某个初始的高斯分布
2. 当新数据产生时，通过极线搜索和块匹配确定投影点位置
3. 根据几何关系计算三角化之后的深度及不确定性
4. 将当前观测融合进上一次的估计中。若收敛则停止计算，否则返回第二步

1.2 像素梯度问题

块匹配的正确与否依赖于图像块是否具有区分度，如果图像块是一片黑或者一片白，则难以匹配。

有明显梯度的小块将具有良好的区分度，不易引起误匹配。对于梯度不明显的像素，由于块匹配没有区分性，将难以有效地估计其深度。所以，像素梯度明显的地方，也就是有明显纹理的物体，得到的深度信息也相对准确。所以反映了立体视觉中一个非常常见的问题：对物体纹理的依赖性。

以上问题无法在现有的算法流程上加以改进并解决。现在说一下两种极端情况：

1. 像素梯度平行于极线方向：在平行的例子里，我们能够精确地确定匹配度最高点出现在何处，匹配效果好。
2. 像素梯度垂直于极线方向：即使小块有明显梯度，但是我们沿着极线做块匹配时，会发现匹配成都都是一样的，因此得不到有效的匹配，匹配效果差。

（注：理解极线的方向和梯度的方向，可看图）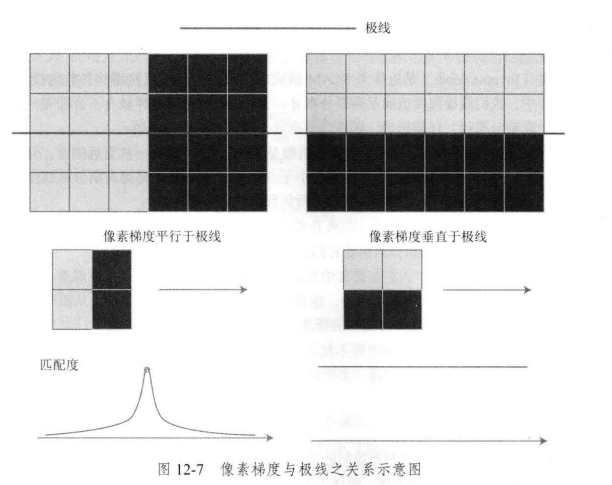

但实际情况往往处于像素梯度与极限方向垂直和平行之间。所以夹角越小（趋近于平行）匹配的不确定性变小 ，反之变大。

1.3 逆深度

没太看明白，大概意思是关于一个三维点的参数化形式是否合理？是否可以用高斯分布？是否独立？根据以上探讨，人们在仿真中发现，假设深度的倒数，也就是逆深度，为高斯分布是比较有效的。随后，在实际应用中，逆深度也具有更好的数值稳定性，从而逐渐成为一种通用的技巧，存在与现有SLAM方案中的标准做法中。

1.4 图像间的变换

在块匹配事前，做一次图想到图像间的变换是一种常见的预处理方式。我们做块匹配是通过像素值来完成的，当相机旋转式，一块上黑下白的图像块可能会变成上白下黑，导致匹配相关性直接为负值。因此，为了防止这样的情况出现，我们在匹配前把参考帧与当前参考帧之间的运动考虑进来。

方法：将当前帧和草看诊通过关系式（看书）建立起放射变换矩阵，这样就可以对当前帧进行放射变换，在进行块匹配。

1.5 并行化：效率的问题

CPU读取图片是通过循环遍历，是串行的，非常慢。由于这几十万个像素点的深度是彼此无关的，我们可以使用GPU进行并行加速运算。因此，在单目和双目的稠密重建中，经常看到利用GPU进行并行加速的方式。利用GPU的稠密深度估计是可以在主流GPU上实时化的。

2. RGB-D稠密建图

只需了解有多种地图模式，点云地图，占据网格地图（occupancy grid map）（体素，voxel，跟像素对比）。体素建图有体素网络滤波器进行降采样，由于多个视角存在视野重叠，重叠区域会有大量位置相近的点，占用很多空间，体素滤波保证了一个一定大小的立方体（或者说体素）内仅有一个点。

2.1 八叉树地图（octomap）

八叉树是一种在导航中比较常用的、灵活的、压缩的、能随时更新的、本身有较好的压缩性能的地图形式。

我们可以把一个方块等分的切成8个相同大小的小方块，这个步骤可以不断地重复，直到最后的方块达到建模的最高精度。

为什么八叉树地图更省空间？
在八叉树中，在节点中存储他是否被占据的信息。当某个方块的所有子节点都被占据或都不被占据的时候，就没必要展开这个节点。通常有占据的空间点都是相连的，不占据的也是，所以八叉树比点云更节省大量的存储空间。

比如，如果一个块8个子节点都占据，在octomap中只需一个变量即可表示，而点云需要8个变量，这样差距就是8倍。

注：不是所有点都是确定的，对于不确定的点，我们可以动态的处理，用一个浮点数而非二值来表示，当不断的观测时，它被占据就加它，反之就减。但是这样可能会超过0到1的范围，所以可以用概率对数值logit来处理。

3. 三维重建

三维重建与SLAM非常相似但又有少许不同。