最近在学习高翔的视觉SLAM十四讲，在第三章提到了罗德里格斯公式（Rodrigue’s Formula），但书中并没有给出相应的推导公式。在网上搜了不上相关的博客，看了好几篇才看明白，一些基础知识并没有在公式推导过程中给出，导致一开始看得云里雾里。

所以这篇博客就是总结罗德里格斯公式推导过程以及过程中所对应的所有知识点，包括一些基础知识。

推导流程

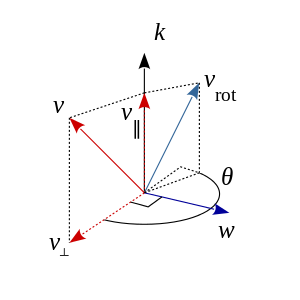
整个推导过程都是围绕这上面这张图展开的，其实是要旋转的向量，是旋转后的向量，是旋转轴方向上的单位向量，是关于旋转轴上的平行分量，是关于旋转轴的垂直分量。

搞清楚定义之后，开始进行推导。

根据向量的加法运算：

现假设为旋转轴上的单位向量，则可以表示为：

其中a和b为与k垂直的平面上的两个向量，可以不用在意，知识表述k和平面的垂直关系，后续只用到k。

那么对于的平行分量和垂直分量，利用向量点乘和叉乘的性质，有：

公式3即点乘的性质，比较好理解。在公式4中，我们知道向量之间叉乘得垂直向量，而k是单位向量，则叉乘相当于绕着k旋转了90°，再叉乘一个k就相当于旋转了180°，方向与相反，所以再加个负号就为垂直分量。至于为什么要这么做，是因为利用叉乘将三个量关联起来，后面的推导会用到。

对于公式4，还有一种推导方法，根据双重向量积（二重矢积，https://baike.baidu.com/item/%E5%8F%8C%E9%87%8D%E5%90%91%E9%87%8F%E7%A7%AF/7385780?fr=aladdin）的性质，对于给定空间的三个向量a,b,c，有，所以可以推出：

在有了三个量之间的关系式后，再求旋转后的向量分量：

那么联立公式4，5，7，8可得：

这是向量叉乘形式，现在转化成矩阵相乘形式。对于向量叉乘，可以转化为矩阵相乘，其中表示a的反对成矩阵，那么将k转化为反对称矩阵K，就有：

联立公式9，10，11，最后得的表达式：

令，则可得罗德里格斯公式：

上面的公式是单位向量k的反对称矩阵形式，将其转成视觉SLAM第三讲的公式形式，可以利用向量投影矩阵。先将公式9转换一下：

因为是v在k上的投影，并且k是单位向量，所以由向量投影矩阵，可得：

最终，联立公式14，15，即可得旋转向量与旋转矩阵之间的转换关系：

相关知识

点乘和叉乘

dot点乘：点乘又称內积。对于，其几何意义有：
① 点乘的结果是a在b上的投影的模乘以b的模
② 描述了向量之间的夹角

矩阵没有点乘一说

cross product叉乘：叉乘又称外积、向量积。对于，其几何意义有：
① 代表了aOb平面的法向量
② 该法向量长度为
③ 上式也代表a和b组成的平行四边形的面积
叉乘形成的法向量成右手法则，所以叉乘的顺序会影响结果。

向量投影和向量投影矩阵

https://blog.csdn.net/wlk1229/article/details/84779370

双重向量积

定义：给定空间的三个向量a,b,c,如果先做其中两个向量a,b的向量积a×b,再做所得向量与第三向量的向量 积，那么最后的结果仍然是一个向量，叫做所给三向量的双重向量积，记做：(a×b)×c。

性质：

• (a×b)×c=(a·c)b-(b·c)a
• a×(b×c)=-(b×c)×a=(a·c)b-(a·b)c