1. 什么是线性？

最简单的解释：
线性=齐次性+可加性

齐次性：f(ax) = af(x) 可加性：f(x+y) = f(x) + f(y)

2. BA

2.1 代价函数、目标函数

代价函数又称为损失函数，有均方差误差、交叉熵误差
目标函数是要进行求解的函数（可以是代价函数、或其变体）

2.2 BA的求解

1. 最小二乘的引出：BA要求解一个最小二乘问题。所以把运动方程抽象为h(T, p)，则误差项为e - h(T, p)
2. 代价函数：这里使用均方差误差作为代价函数，即sum{error}^2 = sum{z - h(T, p)}^2，这个也是目标函数
3. 非线性优化：定义一个初始值，不断求解增量方程。我们把增量定义为整体自变量（包括位姿、内参、三维点等）的增量，这样就得到一个目标函数的变体。定义代价函数关于位姿的偏导数Fij和代价函数关于三维点的偏导数Eij，具体形式参加7.7.3节，最小化投影误差求解PnP。
4. 定义F为每个Fij的拼凑，是整体目标函数关于整体变量的导数。对E也一样。这样我们定义雅可比矩阵为，则，然后我们要计算，无论用什么方式求解，这个计算量都是巨大的，因为H矩阵特别大。所以我们需要利用这里的H的特殊性质（稀疏性）并利用边缘化的方法进行加速求解。

2.3 稀疏性和边缘化

H矩阵的稀疏性是由雅可比矩阵J(x)引起的。如果只考虑这些代价函数的其中一个eij，注意这个误差项只描述了在Ti看到pj这件事，只涉及到第i个相机点和第j个路标点，对其余部分的变量的导数都为0：

这体现了该误差项与其他路标和轨迹无关的特性。而想想，这样H的邻接矩阵（adjacency matrix）就变成了一个镐形。H的左上角和右下角都是对角块矩阵：

我们可以利用这个特性，加速运算，需要用到的方法就是边缘化（marginalization）：
方法是对两边左乘一个矩阵，将H右上角变为0：

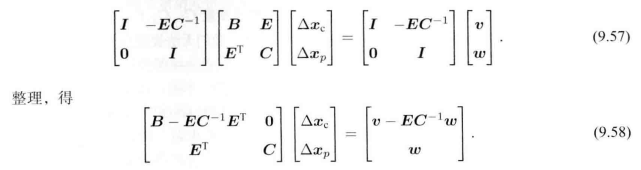
这样子，我们就可以先求出，然后再求另一个。这个过程称为marginalization，或者Schur消元。这样做法的优势在于：

1. 在消元过程中，由于C为对角块矩阵，所以求逆容易解出（只需要求解每一个小对角块矩阵的逆，把它们拼接起来即可，计算量大大降低）
2. 求解了之后，再求解另一个就变得方便，这依然用到了C求逆容易的特性。

所以，整个边缘化的计算量在于求解消元即求解：

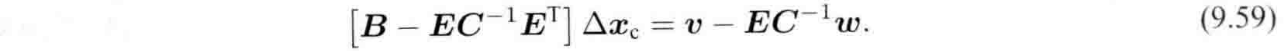
对于9.59式子打的系数方程，我们把它记为S，即H矩阵进行Schur消元后的矩阵，它的稀疏性是不规则的。但是它的邻接矩阵还是有一定的意义：S矩阵的非对角线上的非零矩阵快，表示了该处对应的两个相机变量之间存在这共同观测的路标点，有时称为共视。反之，如果该块为0，则表示这两个相机没有共同观测。

2.3.1 什么是边缘化

边缘化就是把某个未知量通过矩阵恒等变换的方式令其暂时不参与计算，将其与的未知量求出后，被边缘化的量可以自然得到，因此将它们暂时理解为删除也未尝不可。

2.4 鲁邦核函数

为什么需要鲁邦核函数：
在前面的BA中，我们把最小化误差的二范数平方作为目标函数、代价函数。这样很直观，但如果其中一个数据是错的，比如误匹配等原因，这样我们把一条原本不应该加到图的边给加进去了。在算法看来，这相当于我们观测到了一次很不可能产生的数据。这时，在图优化中会有一条误差很大的边，它的梯度也很大，意味着调整它的值性价比很高，所以算法会优先调整这条边所连接的节点的估计值，而忽视（一定程度上的）其他值。

我们可以理解代价函数是损失函数，合适的损失函数对于拟合映射有着深刻的作用。

所以我们需要鲁邦核函数，具体的方式是，把原先误差的二范数度量替换为一个增长没有这么快的函数，同时保证自己的光滑性质（不然没法求导）。比如最常见的Huber核：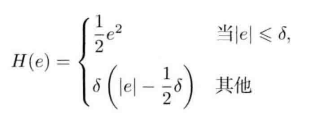

什么是鲁邦核函数：
首先，它是核函数，核函数在SLAM中可以认为是一个代价函数，核函数保证每个边的误差不会大的没边而在求梯度、优化的时候忽视其他的边（比如误匹配的现象），这使得整个优化结果更稳健，所以又称鲁棒核函数。