举个例子

举个例子：
令，问满足这个条件的矩阵的自由度是多少？

• 对于，一共有9个变量，自由度为9。
• 对于A的每一个行向量，比如，只要确定了其中两个元素的值就能算出第三个元素的值（因为），那么自由度减去3。
• 再看，对A乘以任意常数任然满足原等式即，所以是尺度等价的。利用这个性质，我们可以对矩阵A进行一下处理，比如令或者说对A每一个元素除一个，这样，我们就令矩阵A的处的元素为1，然后求其他元素的值，再通过缩放，我们就得到了所有满足条件的矩阵。所以，因为尺度等价性，自由度减1。所以最后问题的答案是：自由度为5.

本质矩阵的自由度

对于本质矩阵E（Essential Matrix），因为，平移和旋转各有3个自由度，故共有6个自由度。但是由于尺度等价性，故实际上有5个自由度。如何理解呢？参照上面的例子，对于对极约束，有：

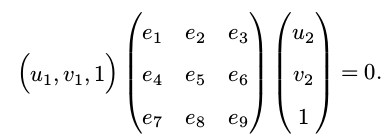
现在把矩阵E展开，写成线性模式：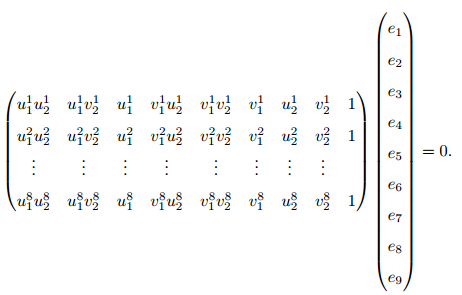

对于左边的的系数矩阵，如果存在解，那么对乘以任意常数k，等式依然成立。所以E具有尺度等价性，自由度减1。如果抛开E这个本质矩阵的约束，考虑任意矩阵，自由度减1后只要求解8个变量即可，这就是八点法（Eight-point-algorithm）的由来。

而从E本质矩阵的角度出发，E具有5个自由度，意思是我们最少可以用5对点来求解E，这就是5点法。

为什么最少能用5个点求解本质矩阵

自由度9-1可以理解，但自由度是6-1。这是我学习时候的困惑。下面给出我的理解：

首先说6个自由度。所谓的本质矩阵E不过是由三个轴上的位移和三个轴上的旋转角度通过一定的组合构成的矩阵。（代入这几个量的公式实在是太难敲了就不敲了），下面只就给出旋转矩阵的公式：

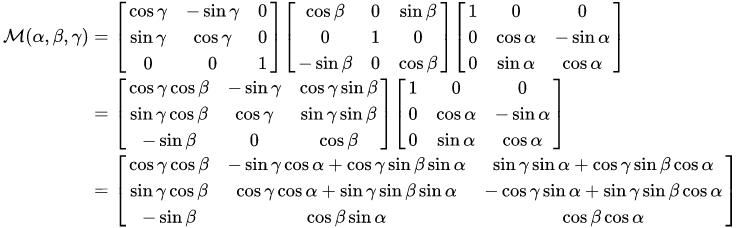
虽然E有9个元素，但是当我们确定了，我们就确定了的值，同理于。所以有9个元素的本质矩阵有6个自由度。但是由于尺度等价性，我们将前文提到的E展开后的向量中的置为1，这里，这个元素涉及到的变量有五个，因为我们将e9置了1，所以当我们知道这五个变量的其中4个之后，剩下一个变量就可以通过这个等式推出来，自由度减1。

以上都是个人见解，如果有不对的地方非常希望大家能够指出来，一起交流~