回溯法

概念

「回溯」就是 深度优先遍历 状态空间的过程中发现的特有的现象，程序会回到以前访问过的结点。而程序在回到以前访问过的结点的时候，就需要将状态变量恢复成为第一次来到该结点的值。

问「一个问题 所有的 解」一般考虑使用回溯算法。因此回溯算法也叫「暴力搜索」，但不同于最粗暴的多个 for 循环，回溯算法是有方向的遍历。

实现细节

解释递归后面状态重置是怎么回事

当回到上一级的时候，所有的状态变量需要重置为第一次来到该结点的状态，这样继续尝试新的选择才有意义；
在代码层面上，需要在递归结束以后，添加递归之前的操作的逆向操作；

基本类型变量和对象类型变量的不同处理

基本类型变量每一次向下传递的时候的行为是复制，所以无需重置；
对象类型变量在遍历的全程只有一份，因此再回退的时候需要重置；
类比于 Java 中的 方法参数 的传递机制：
基本类型变量在方法传递的过程中的行为是复制，每一次传递复制了参数的值；
对象类型变量在方法传递的过程中复制的是对象地址，对象全程在内存中共享地址。

字符串问题的特殊性

如果使用 + 拼接字符串，每一次拼接产生新的字符串，因此无需重置；
如果使用 StringBuilder 拼接字符串，整个搜索的过程 StringBuilder 对象只有一份，需要状态重置。

为什么不是广度优先遍历

广度优先遍历每一层需要保存所有的「状态」，如果状态空间很大，需要占用很大的内存空间；
深度优先遍历只要有路径可以走，就继续尝试走新的路径，不同状态的差距只有一个操作，而广度优先遍历在不同的层之前，状态差异很大，就不能像深度优先遍历一样，可以使用一份状态变量去遍历所有的状态空间，在合适的时候记录状态的值就能得到一个问题的所有的解。

例题

完成「力扣」第 46 题：全排列（中等）；
完成「力扣」第 37 题：数独（困难）；
下面是字符串的搜索问题，完成这些问题可以帮助理解回溯算法的实现细节。

完成「力扣」第 22 题：括号生成（中等）；
完成「力扣」第 17 题：电话号码的字母组合（中等）；
完成「力扣」第 784 题：字母大小写全排列（中等）。

力扣46 全排列

46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3] 输出:

[

[1,2,3],

[1,3,2],

[2,1,3],

[2,3,1],

[3,1,2],

[3,2,1]

]

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/permutations

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>>ret;
        if(nums.size() == 0)
            return ret;
        if(nums.size() == 1)
            return vector<vector<int>>{{nums[0]}};
        for(int i = 0; i < nums.size(); i++)
        {
            vector<int>part(nums.begin(), nums.begin() + i);
            part.insert(part.end(), nums.begin() + i + 1, nums.end());
            vector<vector<int>>tmp_ret = permute(part);
            for(auto &vec : tmp_ret)
            {
                vec.insert(vec.begin(), nums[i]);
                ret.push_back(vec);
            }
        }
        return ret;
    }
};

力扣351 安卓系统手势解锁

351. 安卓系统手势解锁

我们都知道安卓有个手势解锁的界面，是一个 3 x 3 的点所绘制出来的网格。

给你两个整数，分别为 m 和 n，其中 1 ≤ m ≤ n ≤ 9，那么请你统计一下有多少种解锁手势，是至少需要经过 m 个点，但是最多经过不超过 n 个点的。

先来了解下什么是一个有效的安卓解锁手势:

每一个解锁手势必须至少经过 m 个点、最多经过 n 个点。 解锁手势里不能设置经过重复的点。 假如手势中有两个点是顺序经过的，那么这两个点的手势轨迹之间是绝对不能跨过任何未被经过的点。

经过点的顺序不同则表示为不同的解锁手势。

解释:

| 1 | 2 | 3 |

| 4 | 5 | 6 |

| 7 | 8 | 9 |

无效手势：4 - 1 - 3 - 6

连接点 1 和点 3 时经过了未被连接过的 2 号点。

无效手势：4 - 1 - 9 - 2

连接点 1 和点 9 时经过了未被连接过的 5 号点。

有效手势：2 - 4 - 1 - 3 - 6

连接点 1 和点 3 是有效的，因为虽然它经过了点 2 ，但是点 2 在该手势中之前已经被连过了。

有效手势：6 - 5 - 4 - 1 - 9 - 2

连接点 1 和点 9 是有效的，因为虽然它经过了按键 5 ，但是点 5 在该手势中之前已经被连过了。

示例:

输入: m = 1，n = 1

输出: 9

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/android-unlock-patterns

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

概要
自从安卓使用“手势解锁”系统保护手机以免非授权使用之后，一个常被提及的问题是：这个图案的安全性到底有多高？本文将给出这个答案，以呈现以下算法：计算有多少种合法图案。这个算法面向初学者并介绍两个基本概念：回溯和数组。

题解
方法：回溯
算法

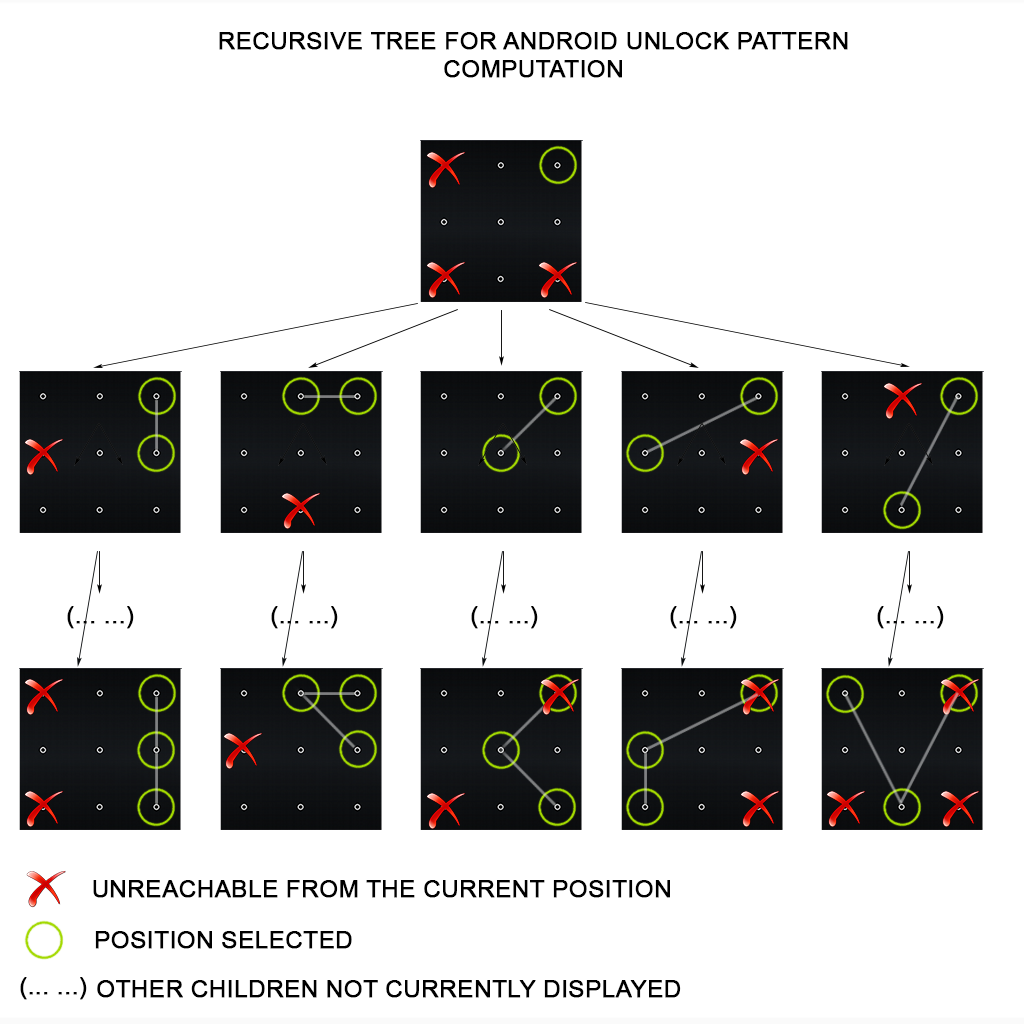
算法适用回溯方法模拟所有可能的 kk 个数字 [1…9][1…9] 的组合，其中 m≤k≤n。在构造递归搜索树的时候，算法会剪枝掉所有不满足规则的方案。

为了计算一个合法手势，算法按照如下步骤进行：

选择一个当前仍然未被使用的数字 ii，这一步通过一个访问数组 usedused 实现，保存所有可用数字。
我们需要记录上一个访问的数字 lastlast。算法需要检查是否满足以下任一条件：
从 lastlast 到 ii 之间是国际象棋中马的移动，或者 lastlast 和 ii 是同一行或列的相邻元素。这种情况下，两个数字之和应当为奇数。
连接 lastlast 和 ii 的中间元素 midmid 已经被访问过，比方说 lastlast 和 ii 选择的是对角线上的两点，那么中间点 mid = 5mid=5 应当已经选过。
lastlast 和 ii 是对角线上的相邻元素。
假设上面有一个条件满足，数字 ii 就变成了合法手势的一部分，算法继续枚举下一个数字，知道整个手势图案被生成。最终计数总方案数。

加入没有任一条件符合，算法当前就不会选择数字 ii，回溯然后继续在未使用的数字中搜索可行的数字。

public class Solution {
    private boolean used[] = new boolean[9];
    public int numberOfPatterns(int m, int n) {            
        int res = 0;
        for (int len = m; len <= n; len++) {                
            res += calcPatterns(-1, len);
            for (int i = 0; i < 9; i++) {                    
                used[i] = false;
            }            
        }
        return res;
    }
    private boolean isValid(int index, int last) {
        if (used[index])
            return false;
        // first digit of the pattern    
        if (last == -1)
            return true;
        // knight moves or adjacent cells (in a row or in a column)           
        if ((index + last) % 2 == 1)
            return true;
        // indexes are at both end of the diagonals for example 0,0, and 8,8          
        int mid = (index + last)/2;
        if (mid == 4)
            return used[mid];
        // adjacent cells on diagonal  - for example 0,0 and 1,0 or 2,0 and //1,1
        if ((index%3 != last%3) && (index/3 != last/3)) {
            return true;
        }
        // all other cells which are not adjacent
        return used[mid];
    }
    private int calcPatterns(int last, int len) {
        if (len == 0)
            return 1;    
        int sum = 0;
        for (int i = 0; i < 9; i++) {
            if (isValid(i, last)) {
                used[i] = true;
                sum += calcPatterns(i, len - 1);
                used[i] = false;                    
            }
        }
        return sum;
    }
}
作者：LeetCode
链接：https://leetcode-cn.com/problems/android-unlock-patterns/solution/an-zhuo-xi-tong-shou-shi-jie-suo-by-leetcode/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

力扣39 组合总和

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。

解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,

所求解集为：

[

[7],

[2,2,3]

]

示例 2：

输入：candidates = [2,3,5], target = 8,

所求解集为：

[

[2,2,2,2],

[2,3,3],

[3,5]

]

提示：

1 <= candidates.length <= 30

1 <= candidates[i] <= 200

candidate 中的每个元素都是独一无二的。

1 <= target <= 500

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/combination-sum

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

回溯法需要注意的是，需要找到回溯终止的条件，在这道题中，已经说明了数组中不存在负数，因此可以把target<0作为回溯终止的条件，如果没有不存在负数这个条件，就需要先对数组进行排序，并判断target是否小于排序后的第一个数，如果小于，则终止回溯。详见第二种解法，另外采用emplace_back可以大大提高程序的效率。同时，这道题也说明了，所有的数字都可以重复使用，所以在下面的解法中传入的start是i而非是i+1.

class Solution {
public:
    void backtrace(vector<int>& candidates, vector<vector<int>>& ret, vector<int>&tmplist, int target, int start)
    {
        if(target < 0)
            return;

        if(target == 0)
        {
            ret.emplace_back(tmplist);
            return;
        }

        for(int i = start; i < candidates.size(); i++)
        {
            tmplist.emplace_back(candidates[i]);
            backtrace(candidates, ret, tmplist, target-candidates[i], i);
            tmplist.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>>ret;
        vector<int>tmplist;
        backtrace(candidates, ret, tmplist, target, 0);
        return ret;
    }
};

如果没有说明数组中全是正数

class Solution {
public:
    void backtrace(vector<int>& candidates, vector<vector<int>>& ret, vector<int>&tmplist, int target, int start)
    {
        if(target < 0)
            return;

        if(target == 0)
        {
            ret.emplace_back(tmplist);
            return;
        }

        for(int i = start; i < candidates.size(); i++)
        {
            tmplist.emplace_back(candidates[i]);
            backtrace(candidates, ret, tmplist, target-candidates[i], i);
            tmplist.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>>ret;
        vector<int>tmplist;
        backtrace(candidates, ret, tmplist, target, 0);
        return ret;
    }
};

力扣47 全排列II

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]

输出：

[[1,1,2],

[1,2,1],

[2,1,1]]

示例 2：

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8

-10 <= nums[i] <= 10

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/permutations-ii

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

在这里进行了剪枝

class Solution {
public:
    vector<vector<int>> backtrace(vector<int> nums)
    {
        vector<vector<int>>ret;
        if(nums.size() == 0)
            return ret;

        if(nums.size() == 1)
            return vector<vector<int>>{{nums[0]}};

        for(int i = 0; i < nums.size(); i++)
        {
            if(i > 0 && nums[i] == nums[i-1])
                continue;

            vector<int>part(nums.begin(), nums.begin() + i);
            part.insert(part.end(), nums.begin() + i + 1, nums.end());

            vector<vector<int>>partres = backtrace(part);

            for(auto vec : partres)
            {
                vec.insert(vec.begin(), nums[i]);
                ret.emplace_back(vec);
            }
        }

        return ret;
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return backtrace(nums);
    }
};

力扣22 括号生成

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3

输出：[“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]

示例 2：

输入：n = 1

输出：[“()”]

提示：

1 <= n <= 8

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/generate-parentheses

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
public:
    void backtrack(vector<string>& ans, string& cur, int open, int close, int n)
    {
        if(cur.size() == n * 2)
        {
            ans.push_back(cur);
            return;
        }

        if(open < n)
        {
            cur.push_back('(');
            backtrack(ans, cur, open + 1, close, n);
            cur.pop_back();
        }

        if(close < open)
        {
            cur.push_back(')');
            backtrack(ans, cur, open, close + 1, n);
            cur.pop_back();
        }
    }
    vector<string> generateParenthesis(int n) {
        vector<string> result;
        string current;
        backtrack(result, current, 0, 0, n);
        return result;
    }
};

力扣51 N皇后

51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

输入：n = 4 输出：[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]] 解释：如上图所示，4 皇后问题存在两个不同的解法。 示例 2：

输入：n = 1 输出：[[“Q”]]

提示：

1 <= n <= 9 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/n-queens 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
public:
    void quenePos(int currow, vector<pair<int, int>>& forbiden, int n)
    {
        if(currow >= n)
        {
            vector<string>tmp;
            for(int i = 0; i < n; ++i)
            {
                string str(n, '.');  
                int col = forbiden[i].second;
                str[col] = 'Q';
                tmp.push_back(str);

            }
            ret.push_back(tmp);
            return;
        }

        for(int col = 0; col < n; col++)
        {
            bool place = true;
            for(int tmp = 0; tmp < forbiden.size(); tmp++)
            {
                int forbidenrow = forbiden[tmp].first;
                int forbidencol = forbiden[tmp].second;
                int gaprow = currow - forbidenrow;
                if((col == forbidencol - gaprow) || (col == forbidencol) || (col == forbidencol + gaprow))
                {
                    place = false;
                    break;
                }

            }

            if(!place)
                continue;

            pair<int, int>position{currow, col};
            forbiden.push_back(position);
            quenePos(currow + 1, forbiden, n);
            forbiden.pop_back();
        }

        return;
    }

    vector<vector<string>> solveNQueens(int n) {
        ret.clear();
        vector<pair<int, int>>forbiden;
        quenePos(0, forbiden, n);
        return ret;

    }
private:
    vector<vector<string>> ret;
};