字符串

151 字符串反转

151. Reverse Words in a String
Given an input string, reverse the string word by word.

Example 1: Input: “the sky is blue“ Output: “blue is sky the“

Example 2: Input: “ hello world! “ Output: “world! hello” Explanation: Your reversed string should not contain leading or trailing spaces.

Example 3:

Input: “a good example”

Output: “example good a”

Explanation: You need to reduce multiple spaces between two words to a single space in the reversed string.

Note:

  • A word is defined as a sequence of non-space characters.
  • Input string may contain leading or trailing spaces. However, your reversed string should not contain leading or trailing spaces.
  • You need to reduce multiple spaces between two words to a single space in the reversed string.

Follow up:

For C programmers, try to solve it in-place in O(1) extra space.

  1. class Solution(object):
  2.     def reverseWords(self, s):
  3.         """
  4.         :type s: str
  5.         :rtype: str
  6.         """
  7.         slist = s.split()
  8.         revertlist = slist[::-1]
  9.         ret=""
  10.         for tmp in revertlist:
  11.             ret += tmp + " "
  12.         return ret[:-1]

collections

这个模块实现了特定目标的容器，以提供Python标准内建容器 dict , list , set , 和 tuple 的替代选择。

namedtuple() 创建命名元组子类的工厂函数
deque 类似列表(list)的容器，实现了在两端快速添加(append)和弹出(pop)
ChainMap 类似字典(dict)的容器类，将多个映射集合到一个视图里面
Counter 字典的子类，提供了可哈希对象的计数功能
OrderedDict 字典的子类，保存了他们被添加的顺序
defaultdict 字典的子类，提供了一个工厂函数，为字典查询提供一个默认值
UserDict 封装了字典对象，简化了字典子类化
UserList 封装了列表对象，简化了列表子类化
UserString 封装了列表对象，简化了字符串子类化

Counter

class collections.Counter([iterable-or-mapping])

一个 Counter 是一个 dict 的子类，用于计数可哈希对象。它是一个集合，元素像字典键(key)一样存储，它们的计数存储为值。计数可以是任何整数值，包括0和负数。 Counter 类有点像其他语言中的 bags或multisets。

  1. >>> from collections import Counter
  2. >>> c = Counter() # a new, empty counter
  3. >>> c
  4. Counter()
  5. >>> c = Counter('gallahad') # a new counter from an iterable
  6. >>> c
  7. Counter({'a': 3, 'l': 2, 'g': 1, 'h': 1, 'd': 1})
  8. >>> c = Counter({'red':4, 'blue': 2}) # a new counter from a mapping
  9. >>> c
  10. Counter({'red': 4, 'blue': 2}) 
  11. >>> c = Counter(cats=4, dogs=8) # a new counter from keywords args
  12. >>> c
  13. Counter({'dogs': 8, 'cats': 4})

347 前K个高频元素

347. 前 K 个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2

输出: [1,2]

示例 2:

输入: nums = [1], k = 1

输出: [1]

提示：

你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。

你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。

题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。

你可以按任意顺序返回答案。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/top-k-frequent-elements

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

方法一：Heap

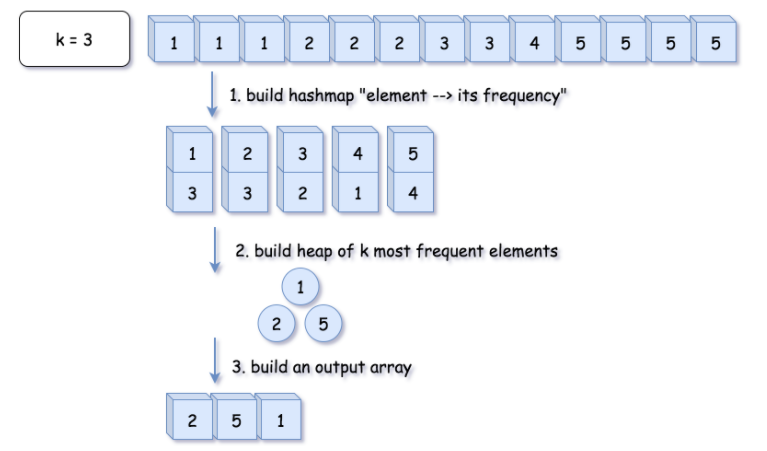
image.png

  1. from collections import Counter
  2. class Solution:
  3.     def topKFrequent(self, nums: List[int], k: int) -> List[int]: 
  4.         # O(1) time 
  5.         if k == len(nums):
  6.             return nums
  8.         # 1. build hash map : character and how often it appears
  9.         # O(N) time
  10.         count = Counter(nums)   
  11.         # 2-3. build heap of top k frequent elements and
  12.         # convert it into an output array
  13.         # O(N log k) time
  14.         return heapq.nlargest(k, count.keys(), key=count.get)

复杂度分析
时间复杂度：O(Nlog(k))。Counter 方法的复杂度是 O(N)，建堆和输出的复杂度是 O(Nlog(k))。因此总复杂度为 O(N + N log(k)) =O(Nlog(k))。
空间复杂度：O(N)O(N)，存储哈希表的开销。
注释
根据复杂度分析，方法对于小 k 的情况是很优的。但是如果 k 值很大，我们可以将算法改成删除频率最低的若干个元素。

方法二：Quickselect

Hoare’s selection algorithm

Quickselect is a textbook algorthm typically used to solve the problems “find kth something”: kth smallest, kth largest, kth most frequent, kth less frequent, etc. Like quicksort, quickselect was developed by Tony Hoare, and also known as Hoare’s selection algorithm.

参考资料

Lib/heapq.py

  1. # -*- coding: latin-1 -*-
  3. """Heap queue algorithm (a.k.a. priority queue).
  5. Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
  6. all k, counting elements from 0.  For the sake of comparison,
  7. non-existing elements are considered to be infinite.  The interesting
  8. property of a heap is that a[0] is always its smallest element.
  10. Usage:
  12. heap = []            # creates an empty heap
  13. heappush(heap, item) # pushes a new item on the heap
  14. item = heappop(heap) # pops the smallest item from the heap
  15. item = heap[0]       # smallest item on the heap without popping it
  16. heapify(x)           # transforms list into a heap, in-place, in linear time
  17. item = heapreplace(heap, item) # pops and returns smallest item, and adds
  18.                                # new item; the heap size is unchanged
  20. Our API differs from textbook heap algorithms as follows:
  22. - We use 0-based indexing.  This makes the relationship between the
  23.   index for a node and the indexes for its children slightly less
  24.   obvious, but is more suitable since Python uses 0-based indexing.
  26. - Our heappop() method returns the smallest item, not the largest.
  28. These two make it possible to view the heap as a regular Python list
  29. without surprises: heap[0] is the smallest item, and heap.sort()
  30. maintains the heap invariant!
  31. """
  33. # Original code by Kevin O'Connor, augmented by Tim Peters and Raymond Hettinger
  35. __about__ = """Heap queues
  37. [explanation by Fran�ois Pinard]
  39. Heaps are arrays for which a[k] <= a[2*k+1] and a[k] <= a[2*k+2] for
  40. all k, counting elements from 0.  For the sake of comparison,
  41. non-existing elements are considered to be infinite.  The interesting
  42. property of a heap is that a[0] is always its smallest element.
  44. The strange invariant above is meant to be an efficient memory
  45. representation for a tournament.  The numbers below are `k', not a[k]:
  47.                                    0
  49.                   1                                 2
  51.           3               4                5               6
  53.       7       8       9       10      11      12      13      14
  55.     15 16   17 18   19 20   21 22   23 24   25 26   27 28   29 30
  58. In the tree above, each cell `k' is topping `2*k+1' and `2*k+2'.  In
  59. a usual binary tournament we see in sports, each cell is the winner
  60. over the two cells it tops, and we can trace the winner down the tree
  61. to see all opponents s/he had.  However, in many computer applications
  62. of such tournaments, we do not need to trace the history of a winner.
  63. To be more memory efficient, when a winner is promoted, we try to
  64. replace it by something else at a lower level, and the rule becomes
  65. that a cell and the two cells it tops contain three different items,
  66. but the top cell "wins" over the two topped cells.
  68. If this heap invariant is protected at all time, index 0 is clearly
  69. the overall winner.  The simplest algorithmic way to remove it and
  70. find the "next" winner is to move some loser (let's say cell 30 in the
  71. diagram above) into the 0 position, and then percolate this new 0 down
  72. the tree, exchanging values, until the invariant is re-established.
  73. This is clearly logarithmic on the total number of items in the tree.
  74. By iterating over all items, you get an O(n ln n) sort.
  76. A nice feature of this sort is that you can efficiently insert new
  77. items while the sort is going on, provided that the inserted items are
  78. not "better" than the last 0'th element you extracted.  This is
  79. especially useful in simulation contexts, where the tree holds all
  80. incoming events, and the "win" condition means the smallest scheduled
  81. time.  When an event schedule other events for execution, they are
  82. scheduled into the future, so they can easily go into the heap.  So, a
  83. heap is a good structure for implementing schedulers (this is what I
  84. used for my MIDI sequencer :-).
  86. Various structures for implementing schedulers have been extensively
  87. studied, and heaps are good for this, as they are reasonably speedy,
  88. the speed is almost constant, and the worst case is not much different
  89. than the average case.  However, there are other representations which
  90. are more efficient overall, yet the worst cases might be terrible.
  92. Heaps are also very useful in big disk sorts.  You most probably all
  93. know that a big sort implies producing "runs" (which are pre-sorted
  94. sequences, which size is usually related to the amount of CPU memory),
  95. followed by a merging passes for these runs, which merging is often
  96. very cleverly organised[1].  It is very important that the initial
  97. sort produces the longest runs possible.  Tournaments are a good way
  98. to that.  If, using all the memory available to hold a tournament, you
  99. replace and percolate items that happen to fit the current run, you'll
  100. produce runs which are twice the size of the memory for random input,
  101. and much better for input fuzzily ordered.
  103. Moreover, if you output the 0'th item on disk and get an input which
  104. may not fit in the current tournament (because the value "wins" over
  105. the last output value), it cannot fit in the heap, so the size of the
  106. heap decreases.  The freed memory could be cleverly reused immediately
  107. for progressively building a second heap, which grows at exactly the
  108. same rate the first heap is melting.  When the first heap completely
  109. vanishes, you switch heaps and start a new run.  Clever and quite
  110. effective!
  112. In a word, heaps are useful memory structures to know.  I use them in
  113. a few applications, and I think it is good to keep a `heap' module
  114. around. :-)
  116. --------------------
  117. [1] The disk balancing algorithms which are current, nowadays, are
  118. more annoying than clever, and this is a consequence of the seeking
  119. capabilities of the disks.  On devices which cannot seek, like big
  120. tape drives, the story was quite different, and one had to be very
  121. clever to ensure (far in advance) that each tape movement will be the
  122. most effective possible (that is, will best participate at
  123. "progressing" the merge).  Some tapes were even able to read
  124. backwards, and this was also used to avoid the rewinding time.
  125. Believe me, real good tape sorts were quite spectacular to watch!
  126. From all times, sorting has always been a Great Art! :-)
  127. """
  129. __all__ = ['heappush', 'heappop', 'heapify', 'heapreplace', 'merge',
  130.            'nlargest', 'nsmallest', 'heappushpop']
  132. from itertools import islice, count, imap, izip, tee, chain
  133. from operator import itemgetter
  135. def cmp_lt(x, y):
  136.     # Use __lt__ if available; otherwise, try __le__.
  137.     # In Py3.x, only __lt__ will be called.
  138.     return (x < y) if hasattr(x, '__lt__') else (not y <= x)
  140. def heappush(heap, item):
  141.     """Push item onto heap, maintaining the heap invariant."""
  142.     heap.append(item)
  143.     _siftdown(heap, 0, len(heap)-1)
  145. def heappop(heap):
  146.     """Pop the smallest item off the heap, maintaining the heap invariant."""
  147.     lastelt = heap.pop()    # raises appropriate IndexError if heap is empty
  148.     if heap:
  149.         returnitem = heap[0]
  150.         heap[0] = lastelt
  151.         _siftup(heap, 0)
  152.     else:
  153.         returnitem = lastelt
  154.     return returnitem
  156. def heapreplace(heap, item):
  157.     """Pop and return the current smallest value, and add the new item.
  159.     This is more efficient than heappop() followed by heappush(), and can be
  160.     more appropriate when using a fixed-size heap.  Note that the value
  161.     returned may be larger than item!  That constrains reasonable uses of
  162.     this routine unless written as part of a conditional replacement:
  164.         if item > heap[0]:
  165.             item = heapreplace(heap, item)
  166.     """
  167.     returnitem = heap[0]    # raises appropriate IndexError if heap is empty
  168.     heap[0] = item
  169.     _siftup(heap, 0)
  170.     return returnitem
  172. def heappushpop(heap, item):
  173.     """Fast version of a heappush followed by a heappop."""
  174.     if heap and cmp_lt(heap[0], item):
  175.         item, heap[0] = heap[0], item
  176.         _siftup(heap, 0)
  177.     return item
  179. def heapify(x):
  180.     """Transform list into a heap, in-place, in O(len(x)) time."""
  181.     n = len(x)
  182.     # Transform bottom-up.  The largest index there's any point to looking at
  183.     # is the largest with a child index in-range, so must have 2*i + 1 < n,
  184.     # or i < (n-1)/2.  If n is even = 2*j, this is (2*j-1)/2 = j-1/2 so
  185.     # j-1 is the largest, which is n//2 - 1.  If n is odd = 2*j+1, this is
  186.     # (2*j+1-1)/2 = j so j-1 is the largest, and that's again n//2-1.
  187.     for i in reversed(xrange(n//2)):
  188.         _siftup(x, i)
  190. def _heappushpop_max(heap, item):
  191.     """Maxheap version of a heappush followed by a heappop."""
  192.     if heap and cmp_lt(item, heap[0]):
  193.         item, heap[0] = heap[0], item
  194.         _siftup_max(heap, 0)
  195.     return item
  197. def _heapify_max(x):
  198.     """Transform list into a maxheap, in-place, in O(len(x)) time."""
  199.     n = len(x)
  200.     for i in reversed(range(n//2)):
  201.         _siftup_max(x, i)
  203. def nlargest(n, iterable):
  204.     """Find the n largest elements in a dataset.
  206.     Equivalent to:  sorted(iterable, reverse=True)[:n]
  207.     """
  208.     if n < 0:
  209.         return []
  210.     it = iter(iterable)
  211.     result = list(islice(it, n))
  212.     if not result:
  213.         return result
  214.     heapify(result)
  215.     _heappushpop = heappushpop
  216.     for elem in it:
  217.         _heappushpop(result, elem)
  218.     result.sort(reverse=True)
  219.     return result
  221. def nsmallest(n, iterable):
  222.     """Find the n smallest elements in a dataset.
  224.     Equivalent to:  sorted(iterable)[:n]
  225.     """
  226.     if n < 0:
  227.         return []
  228.     it = iter(iterable)
  229.     result = list(islice(it, n))
  230.     if not result:
  231.         return result
  232.     _heapify_max(result)
  233.     _heappushpop = _heappushpop_max
  234.     for elem in it:
  235.         _heappushpop(result, elem)
  236.     result.sort()
  237.     return result
  239. # 'heap' is a heap at all indices >= startpos, except possibly for pos.  pos
  240. # is the index of a leaf with a possibly out-of-order value.  Restore the
  241. # heap invariant.
  242. def _siftdown(heap, startpos, pos):
  243.     newitem = heap[pos]
  244.     # Follow the path to the root, moving parents down until finding a place
  245.     # newitem fits.
  246.     while pos > startpos:
  247.         parentpos = (pos - 1) >> 1
  248.         parent = heap[parentpos]
  249.         if cmp_lt(newitem, parent):
  250.             heap[pos] = parent
  251.             pos = parentpos
  252.             continue
  253.         break
  254.     heap[pos] = newitem
  256. # The child indices of heap index pos are already heaps, and we want to make
  257. # a heap at index pos too.  We do this by bubbling the smaller child of
  258. # pos up (and so on with that child's children, etc) until hitting a leaf,
  259. # then using _siftdown to move the oddball originally at index pos into place.
  260. #
  261. # We *could* break out of the loop as soon as we find a pos where newitem <=
  262. # both its children, but turns out that's not a good idea, and despite that
  263. # many books write the algorithm that way.  During a heap pop, the last array
  264. # element is sifted in, and that tends to be large, so that comparing it
  265. # against values starting from the root usually doesn't pay (= usually doesn't
  266. # get us out of the loop early).  See Knuth, Volume 3, where this is
  267. # explained and quantified in an exercise.
  268. #
  269. # Cutting the # of comparisons is important, since these routines have no
  270. # way to extract "the priority" from an array element, so that intelligence
  271. # is likely to be hiding in custom __cmp__ methods, or in array elements
  272. # storing (priority, record) tuples.  Comparisons are thus potentially
  273. # expensive.
  274. #
  275. # On random arrays of length 1000, making this change cut the number of
  276. # comparisons made by heapify() a little, and those made by exhaustive
  277. # heappop() a lot, in accord with theory.  Here are typical results from 3
  278. # runs (3 just to demonstrate how small the variance is):
  279. #
  280. # Compares needed by heapify     Compares needed by 1000 heappops
  281. # --------------------------     --------------------------------
  282. # 1837 cut to 1663               14996 cut to 8680
  283. # 1855 cut to 1659               14966 cut to 8678
  284. # 1847 cut to 1660               15024 cut to 8703
  285. #
  286. # Building the heap by using heappush() 1000 times instead required
  287. # 2198, 2148, and 2219 compares:  heapify() is more efficient, when
  288. # you can use it.
  289. #
  290. # The total compares needed by list.sort() on the same lists were 8627,
  291. # 8627, and 8632 (this should be compared to the sum of heapify() and
  292. # heappop() compares):  list.sort() is (unsurprisingly!) more efficient
  293. # for sorting.
  295. def _siftup(heap, pos):
  296.     endpos = len(heap)
  297.     startpos = pos
  298.     newitem = heap[pos]
  299.     # Bubble up the smaller child until hitting a leaf.
  300.     childpos = 2*pos + 1    # leftmost child position
  301.     while childpos < endpos:
  302.         # Set childpos to index of smaller child.
  303.         rightpos = childpos + 1
  304.         if rightpos < endpos and not cmp_lt(heap[childpos], heap[rightpos]):
  305.             childpos = rightpos
  306.         # Move the smaller child up.
  307.         heap[pos] = heap[childpos]
  308.         pos = childpos
  309.         childpos = 2*pos + 1
  310.     # The leaf at pos is empty now.  Put newitem there, and bubble it up
  311.     # to its final resting place (by sifting its parents down).
  312.     heap[pos] = newitem
  313.     _siftdown(heap, startpos, pos)
  315. def _siftdown_max(heap, startpos, pos):
  316.     'Maxheap variant of _siftdown'
  317.     newitem = heap[pos]
  318.     # Follow the path to the root, moving parents down until finding a place
  319.     # newitem fits.
  320.     while pos > startpos:
  321.         parentpos = (pos - 1) >> 1
  322.         parent = heap[parentpos]
  323.         if cmp_lt(parent, newitem):
  324.             heap[pos] = parent
  325.             pos = parentpos
  326.             continue
  327.         break
  328.     heap[pos] = newitem
  330. def _siftup_max(heap, pos):
  331.     'Maxheap variant of _siftup'
  332.     endpos = len(heap)
  333.     startpos = pos
  334.     newitem = heap[pos]
  335.     # Bubble up the larger child until hitting a leaf.
  336.     childpos = 2*pos + 1    # leftmost child position
  337.     while childpos < endpos:
  338.         # Set childpos to index of larger child.
  339.         rightpos = childpos + 1
  340.         if rightpos < endpos and not cmp_lt(heap[rightpos], heap[childpos]):
  341.             childpos = rightpos
  342.         # Move the larger child up.
  343.         heap[pos] = heap[childpos]
  344.         pos = childpos
  345.         childpos = 2*pos + 1
  346.     # The leaf at pos is empty now.  Put newitem there, and bubble it up
  347.     # to its final resting place (by sifting its parents down).
  348.     heap[pos] = newitem
  349.     _siftdown_max(heap, startpos, pos)
  351. # If available, use C implementation
  352. try:
  353.     from _heapq import *
  354. except ImportError:
  355.     pass
  357. def merge(*iterables):
  358.     '''Merge multiple sorted inputs into a single sorted output.
  360.     Similar to sorted(itertools.chain(*iterables)) but returns a generator,
  361.     does not pull the data into memory all at once, and assumes that each of
  362.     the input streams is already sorted (smallest to largest).
  364.     >>> list(merge([1,3,5,7], [0,2,4,8], [5,10,15,20], [], [25]))
  365.     [0, 1, 2, 3, 4, 5, 5, 7, 8, 10, 15, 20, 25]
  367.     '''
  368.     _heappop, _heapreplace, _StopIteration = heappop, heapreplace, StopIteration
  369.     _len = len
  371.     h = []
  372.     h_append = h.append
  373.     for itnum, it in enumerate(map(iter, iterables)):
  374.         try:
  375.             next = it.next
  376.             h_append([next(), itnum, next])
  377.         except _StopIteration:
  378.             pass
  379.     heapify(h)
  381.     while _len(h) > 1:
  382.         try:
  383.             while 1:
  384.                 v, itnum, next = s = h[0]
  385.                 yield v
  386.                 s[0] = next()               # raises StopIteration when exhausted
  387.                 _heapreplace(h, s)          # restore heap condition
  388.         except _StopIteration:
  389.             _heappop(h)                     # remove empty iterator
  390.     if h:
  391.         # fast case when only a single iterator remains
  392.         v, itnum, next = h[0]
  393.         yield v
  394.         for v in next.__self__:
  395.             yield v
  397. # Extend the implementations of nsmallest and nlargest to use a key= argument
  398. _nsmallest = nsmallest
  399. def nsmallest(n, iterable, key=None):
  400.     """Find the n smallest elements in a dataset.
  402.     Equivalent to:  sorted(iterable, key=key)[:n]
  403.     """
  404.     # Short-cut for n==1 is to use min() when len(iterable)>0
  405.     if n == 1:
  406.         it = iter(iterable)
  407.         head = list(islice(it, 1))
  408.         if not head:
  409.             return []
  410.         if key is None:
  411.             return [min(chain(head, it))]
  412.         return [min(chain(head, it), key=key)]
  414.     # When n>=size, it's faster to use sorted()
  415.     try:
  416.         size = len(iterable)
  417.     except (TypeError, AttributeError):
  418.         pass
  419.     else:
  420.         if n >= size:
  421.             return sorted(iterable, key=key)[:n]
  423.     # When key is none, use simpler decoration
  424.     if key is None:
  425.         it = izip(iterable, count())                        # decorate
  426.         result = _nsmallest(n, it)
  427.         return map(itemgetter(0), result)                   # undecorate
  429.     # General case, slowest method
  430.     in1, in2 = tee(iterable)
  431.     it = izip(imap(key, in1), count(), in2)                 # decorate
  432.     result = _nsmallest(n, it)
  433.     return map(itemgetter(2), result)                       # undecorate
  435. _nlargest = nlargest
  436. def nlargest(n, iterable, key=None):
  437.     """Find the n largest elements in a dataset.
  439.     Equivalent to:  sorted(iterable, key=key, reverse=True)[:n]
  440.     """
  442.     # Short-cut for n==1 is to use max() when len(iterable)>0
  443.     if n == 1:
  444.         it = iter(iterable)
  445.         head = list(islice(it, 1))
  446.         if not head:
  447.             return []
  448.         if key is None:
  449.             return [max(chain(head, it))]
  450.         return [max(chain(head, it), key=key)]
  452.     # When n>=size, it's faster to use sorted()
  453.     try:
  454.         size = len(iterable)
  455.     except (TypeError, AttributeError):
  456.         pass
  457.     else:
  458.         if n >= size:
  459.             return sorted(iterable, key=key, reverse=True)[:n]
  461.     # When key is none, use simpler decoration
  462.     if key is None:
  463.         it = izip(iterable, count(0,-1))                    # decorate
  464.         result = _nlargest(n, it)
  465.         return map(itemgetter(0), result)                   # undecorate
  467.     # General case, slowest method
  468.     in1, in2 = tee(iterable)
  469.     it = izip(imap(key, in1), count(0,-1), in2)             # decorate
  470.     result = _nlargest(n, it)
  471.     return map(itemgetter(2), result)                       # undecorate
  473. if __name__ == "__main__":
  474.     +
  475. −# Simple sanity test
  476.     heap = []
  477.     data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
  478.     for item in data:
  479.         heappush(heap, item)
  480.     sort = []
  481.     while heap:
  482.         sort.append(heappop(heap))
  483.     print sort
  485.     import doctest
  486.     doctest.testmod()

530 检测大写字母

520. 检测大写字母

给定一个单词，你需要判断单词的大写使用是否正确。

我们定义，在以下情况时，单词的大写用法是正确的：

全部字母都是大写，比如”USA”。

单词中所有字母都不是大写，比如”leetcode”。

如果单词不只含有一个字母，只有首字母大写， 比如 “Google”。

否则，我们定义这个单词没有正确使用大写字母。

示例 1:

输入: “USA”

输出: True

示例 2:

输入: “FlaG”

输出: False

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/detect-capital

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

对于这道题，我一开始使用的是C++的方法，非常的费脑子，算是按照过程式的思维去考虑到所有可能的情况，并总结规律，最后通过两个bool的flag来维系状态

class Solution {
public:
    bool detectCapitalUse(string word) {
        if(word.size() == 1)
            return true;

        int first = word[0];
        bool no_capitals = false;
        if(first >= 'a' && first <= 'z')
            no_capitals = true;

        int second = word[1];
        bool always_capitals = false;

        if(second >= 'A' && second <= 'Z')
        {
            if(no_capitals)
                return false;
            always_capitals = true;
        }

        if(second >= 'a' && second <= 'z')
            no_capitals = true;

        for(int i = 2; i < word.size(); i++)
        {
            if(word[i] >= 'A' && word[i] <= 'Z')
            {
                if(no_capitals)
                    return false;
            }

            if(word[i] >= 'a' && word[i] <= 'z')
            {
                if(always_capitals)
                    return false;
            }
        }

        return true;
    }
};

下面这种方法是我在评论区中所看到的，采用python，非常的简洁

def detectCapitalUse(self, word):
    return word.isupper() or word.islower() or word.istitle()