简介
计算思维是一个有着诸多特点和要求的问题解决过程。计算思维不但对于计算机应用的发展非常重要,而且它也可以用于所有学科的问题解决,包括人文学科、数学和科学等。在完成计算思维的课程后,不但能了解各学科之间的关联,同时也能够体会到课外生活与课堂内知识之间的联系。
计算思维四要素
- 分解:把数据、过程或问题分解成更小的、易于管理或解决的部分
- 模式识别:观察数据的模式、趋势和规律
- 抽象:识别模式形成背后的一般原理
- 算法开发:为解决某一类问题撰写一系列详细的指令
计算思维 vs. 计算机科学
计算机科学是关于信息的研究:如何表征信息?如何优化存储信息?如何处理信息?计算机科学是使用计算机进行计算及其应用的研究。
计算思维则包括编写计算机程序时所使用的技能和思维方式。在已有的课堂教学中使用计算思维的方法和概念能够获得更好的效果。
| 计算思维 | 计算机科学应用 | 学科领域应用 |
|---|---|---|
| 把问题分解为若干部分或步骤 | 将计算图表问题拆分成四部分来处理,每部分由不同的计算机程序独立完成 | 文学:通过对韵律、韵文、意象、结构、语气、措词与含义的分析来分析诗歌 |
| 识别并发现模式或趋势 | 可视化数据来比较微芯片材料和计算机速度,并注意到它的发展趋势 | 经济:寻找国家经济增长和下降的循环模式 |
| 开发解决问题或任务步骤的指令 | 编写一个计算机程序来对数据进行排序 | 烹饪艺术:撰写供他人使用的菜谱 |
| 把模式和趋势归纳至规则、原理或见解中 | 相对于复杂的编程,用较少代码实现复数数据结构 | 数学:找出二阶多项式分解法则 |
| 化学:找出化学键(类型)及(分子间)相互作用的规律 |
算法探究
介绍学科领域中的算法实例。认识并理解算法是一种可以提高学习者能力的强大工具,以及该技术可以用来实现算法和完成算法的自动化。
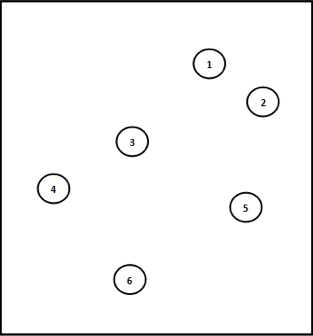
旅行:最短路径
拓展:旅行推销员问题、NP(Non-Deterministic Polynomial, 非确定多项式)问题。旅行推销员问题是计算机科学家所提出的一个经典挑战:为一名旅行推销员规划出一条穿过一个国家的最优路线。
对于该问题来说,找到一条可行路线并不难。你只需要按照你自己的步骤创建一条经过所有城市的路线即可。然而,该问题的困难之处在与:如何确定一条最短路线或者步骤最少的路线,以及是否能在合理的时间内求得一个最优可行方案。
 ->
-> 
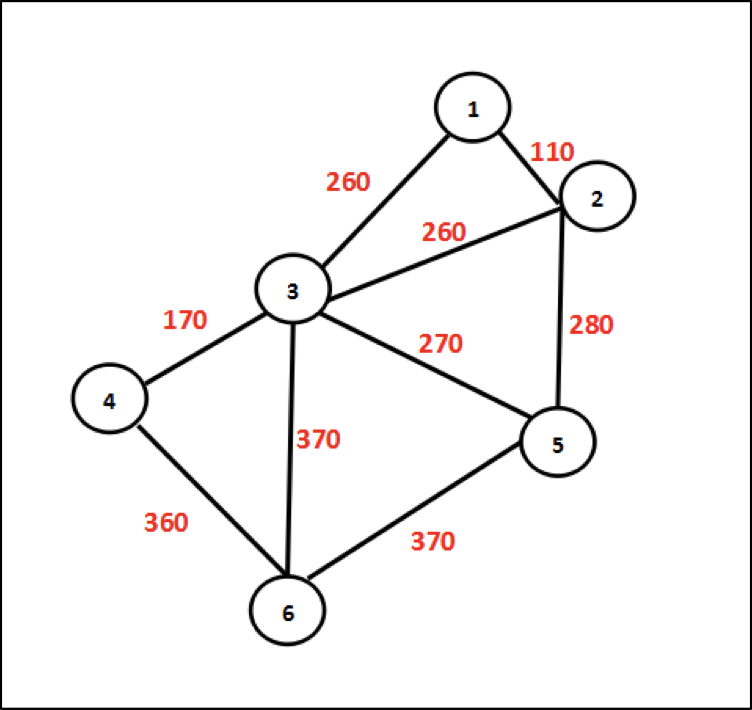
| 距离(公里) | 北京① | 天津② | 石家庄③ | 太原④ | 济南⑤ | 郑州⑥ |
|---|---|---|---|---|---|---|
| 北京① | 0 | 110 | 260 | 400 | 370 | 630 |
| 天津② | 110 | 0 | 260 | 430 | 280 | 580 |
| 石家庄③ | 260 | 260 | 0 | 170 | 270 | 370 |
| 太原④ | 400 | 430 | 170 | 0 | 410 | 360 |
| 济南⑤ | 370 | 280 | 270 | 410 | 0 | 370 |
| 郑州⑥ | 630 | 580 | 370 | 360 | 370 | 0 |
| 距离(公里) | 北京① | 天津② | 石家庄③ | 太原④ | 济南⑤ | 郑州⑥ |
| 郑州⑥ | 630 | 580 | 370 | 360 | 370 | 0 |
| 济南⑤ | 370 | 280 | 270 | 410 | 0 | 370 |
| 太原④ | 400 | 430 | 170 | 0 | 410 | 360 |
| 石家庄③ | 260 | 260 | 0 | 170 | 270 | 370 |
| 天津② | 110 | 0 | 260 | 430 | 280 | 580 |
| 北京① | 0 | 110 | 260 | 400 | 370 | 630 |
| 距离(公里) | 北京① | 天津② | 石家庄③ | 太原④ | 济南⑤ | |
| 郑州⑥ | 630 | 580 | 370 | 360 | 370 | |
| 济南⑤ | 370 | 280 | 270 | 410 | ||
| 太原④ | 400 | 430 | 170 | |||
| 石家庄③ | 260 | 260 | ||||
| 天津② | 110 | |||||
不同路线的结果
| 策略 | 路线 | 距离(公里) |
|---|---|---|
| 1 | ①→②→③→④→⑥→⑤→① | 1640 |
| 2 | ③→②→①→⑤→⑥→④→① | 1640 |
| 3 | ⑤→②→③→⑥→④→①→⑤ | 2010 |
| 4 | ②→⑤→③→④→⑥→①→② | 1820 |
| 5 | … | … |
人文:与时俱进的字词
当我们将算法用计算机技术实现的时候,我们会发现指令的执行要比人工执行快得多。这样的效率优势在处理大规模数据的时候尤为明显。以往需要大量人手共同工作数年才能得出的结果,如今在很短的时间就能得到。
一个经典的计算机应用案例就是我们身边的计算器:从前需要许多人共同合作才能完成计算量,在今天可以用任何袖珍计算器迅速完成。N-gram Viewer 就是一个将算法应用到大规模数据集合中,以获得某些文化中有趣甚至是滑稽的发现。随着越来越多的人了解如何分析数据和整理信息,他们将能够把这些技能应用到新的领域当中,并帮助他们以一种以往难以想象的方式拓展对于宇宙的理解。
数学:元胞自动机
给定一个系统一些初始参数,并规定系统的运行规则,然后让该系统自行运作——该过程我们称之为混沌系统。对于元胞自动机来说,任何一点初始细胞生存状态的或细胞繁殖的规则的变化,都会导致结果的巨大变化。混沌系统广泛存在于天气、交通模式、宇宙学和基因科学中。
科学:基因组学
农民们早已知道动物和植物们已经用相似的特性繁衍后代长达一千多年了。当人们发现所有的生命都使用相同的基因编码和遗传信息时,他们意识到其中蕴含着探索生命奥秘的巨大机会。
从苍蝇的研究中获得的知识可以被应用到猪和其他的物种当中。更加深入的研究人类基因组,了解人类基因组是如何随着时间而变化的,以及发现不同文化的人类种群间的基因差异,都有助于我们改善医疗技术和为人类这个种族留下历史记录。
人类的 DNA 包括数千种不同的基因,而每一种基因都可能需要耗尽一个人的一生来进行研究。算法已经被应用到快速搜索和分析生物样本之中,这能帮助科学家寻找模式与基因突变和某些治疗手段造成的影响。没有任何两个人有着完全一样的基因表现型。深入对于基因的研究将有助于人们了解自身的独特性,并且体会到个体是如何融入更广大的生命群体中的。
模式挖掘
探索学科案例中蕴含的一些模式,并形成一套您独有的、借助模式识别方法进行问题研究的流程。
计算机:数据压缩
| 分解 | 将一整张照片视为许多像素点来处理。 |
|---|---|
| 模式识别 | 应用不同的位掩码,以了解不同的位掩码对图片所需存储空间和图片质量的关系。 |
| 抽象化 | 使用发现的模式来决定使用合适的位掩码,既能够压缩图片体积也能够保持合适的图片质量。 |
| 算法开发 | 你也许已经认识到位掩码的不同属性可以帮助你改善算法的使用。 |
人文:音乐
| 分解 | 观察歌曲的不同部分并将其划分为不同的组成,例如:节拍,音符,以及和声,然后分别检查这些组成成分。 |
|---|---|
| 模式识别 | 调整每个变量,诸如音符的长度以及音阶中音符的频率,来找到一个你最喜欢的设置。 |
| 抽象化 | 添加第三个钢琴来营造和声。 |
| 算法开发 | 调整设置,使用另一种音阶,以及添加额外的钢琴,进行探索。你也许有一些关于音乐其它属性的不同想法,尝试将它们应用到以后对音乐的改进之中。 |
数学:小海龟几何
| 分解 | 将一个任务转换为一系列步伐和转向,例如画一个正方形。 |
|---|---|
| 模式识别 | 观察重复步伐和所画图形的边之间的相互关系。 |
| 抽象化 | 使用转向角度和步伐的数目中的模式来深入了解步伐数目,角度和多边形边的数目之间的关系。 |
| 算法开发 | 设计一个算法用来绘制任意形状的多边形。我们有很多方法来拓展该算法。例如,当计算小海龟的每一步应该多长的时候将边数考虑到。 |
科学:分类
| 分解 | 观察生物体的不同的分类方式。例如:生物体是水生生物或者是有翅膀能在天上飞。 |
|---|---|
| 模式识别 | 研究一种方法用以有效地根据生物体的共同特征来进行分类。 |
| 抽象化 | 测定使用该方法的情况下需要多长时间来进行分类,有助于你了解对所有已知生物体进行分类需要多少问题或分级。 |
| 算法开发 | 在本章节中你并没有开发出一个算法,但是你也许已经想到了如何更有效的对生物进行分类。 |
算法开发
增强你在解决问题过程中应用计算过程的信心,并了解算法是如何清晰地表达一个过程或规则。
计算机:汉诺塔
汉诺塔问题是一个在计算机出现之前就很流行的算法案例。尽管这是一个很有趣的谜题,它也
是一个非常有名的递归和算法效率重要性的例子。随着碟子的数目以线性增加,问题解答步骤的数目以指数增加。在如今,我们在网络和商业交易中使用的算法必须能够处理数十亿用户在一秒内产生的数据。因此,计算机科学家们一直在寻找能够降低算法复杂度而提高算法质量的方法。
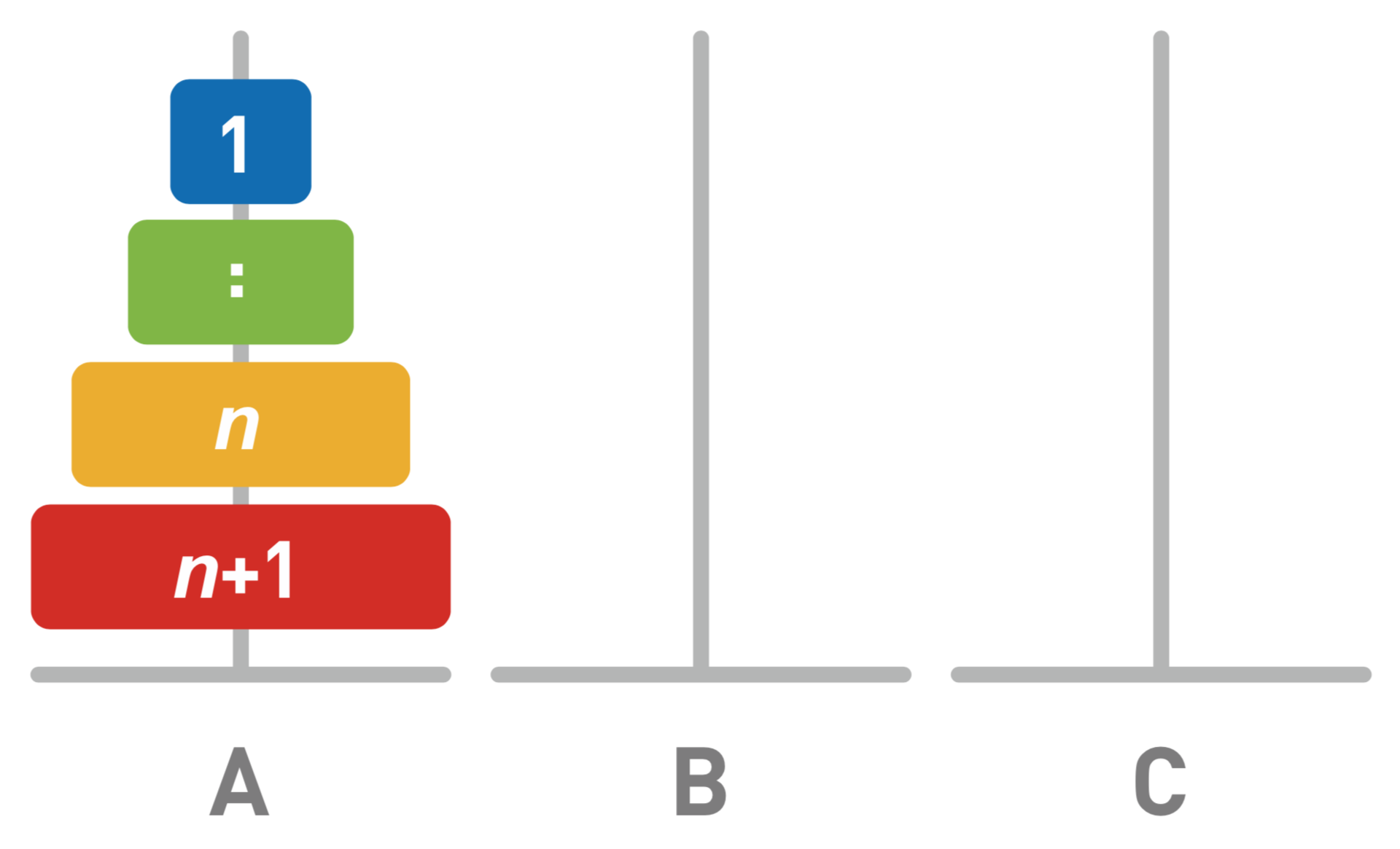

hanoi(n, src, dst, tmp):if n > 0:hanoi(n-1, src, tmp, dst)move disk n from src to dsthanoi(n-1, tmp, dst, src)
def hanoi(n, src, tmp, dst):if n == 1:print(src + ' --> ' + dst)else:hanoi(n-1, src, dst, tmp)print(src + ' --> ' + dst)hanoi(n-1, tmp, src, dst)layer = int(input('number of layers: '))if layer >= 3:hanoi(layer, 'A', 'B', 'C')
人文:聊天机器人
人工智能有可能诞生吗?计算机是否能够和你进行一段对话并不让你意识到它的身份?当计算机在扮演一个人的时候,他需要多少信息呢?我们之所以在活动中选择该算法,是因为他有着相对直观的逻辑。
计算机科学家们在训练他们的算法拓展连接的层级和网络的时候,很像我们自己的大脑在学习新事物的过程。这些算法通常训练用来完成特殊的工作,例如识别一个目标或者解析口语命令。图灵为人工智能设计的测试已经被一个算法通过了,但是这是不可避免的?或是不可能的?
数学:计算器
科学技术和互联网使获得海量的信息成为可能。以往要数个小时才能找到答案的问题,现在只需要几秒钟就能解决,而很复杂的数学方程只要输进计算器就能很快被解答出来。
学生可以自己为课堂创作使用的工具,你有机会为一个计算器来开发算法。使用计算器是一回事,但是为计算器开发一个算法则可以让你更好的理解数学中潜藏的模式。
当你可以清晰的表达和彻底理解数学过程的时候,你就获得了非常深刻的对数学本质的了解。这样,即使在很久以后已经遗忘了具体的数学公式,你也可以将这些理解应用到新的问题之中。
科学:弹力球
实验室是科学家进行试验来验证他们的假设的地方。对某些研究来说,在传统实验室中进行实验是非常困难的,因为它们的研究对象太过微小(例如亚原子微粒),或者需要一个跟地球完全不同的实验环境(例如宇宙中的黑洞),又或者需要极端的环境(例如飞机的测试)。
数十年来,科学家和工程师们通力合作,创造了许多模型和仿真系统来测试他们的理论和原型机。你模拟了一个小球的弹动,并且不断改进这个模型使得它越来越真实。
没有任何一个模拟是完美无缺的,但是只要算法不断改善,仿真就可以帮助我们为一些复杂的现象提供预测,例如全球变暖。科技的成本和仿真软件以及编程语言的可获得性,使得在全球各地进行科学研究称为可能。

