一 GCN做了什么

首先，我们得知道GCN要做什么，现在我们是对CNN网络比较熟悉了，那么在图中加入卷积会做什么呢？这篇博客给了一张图：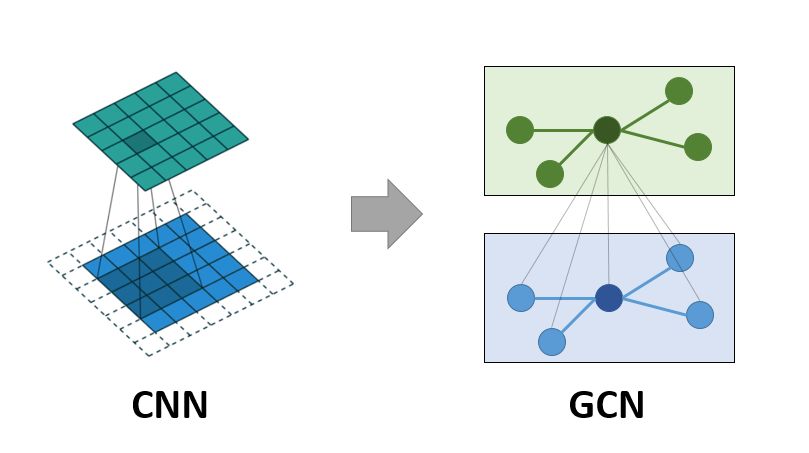
♠ PyT实现GCN - 图2
图1. CNN和GCN的对比
通过上面的PyT消息传递网络中的公式（1），我们可以知道某个节点♠ PyT实现GCN - 图3第♠ PyT实现GCN - 图4层的状态是由♠ PyT实现GCN - 图5层的♠ PyT实现GCN - 图6的状态和其邻边节点♠ PyT实现GCN - 图7的状态通过一些列函数得到的，这个过程对应的就是上图1的GCN
♠ PyT实现GCN - 图8

接下来，就看一下PyT是怎么实现这个过程的：博客原文链接

二 API接口

我们首先调用一下PyT给我们的函数，看看其输入和输出长什么样子

  1. from torch_geometric.nn import GCNConv
  2. import torch
  4. # 定义网络
  5. conv = GCNConv(1, 2)  # emb(in), emb(out)
  6. # 定义边
  7. edge_index = torch.tensor([[1, 2, 3],[0, 0, 0]], dtype=torch.long)  # 2 x E
  8. # 定义输入特征向量
  9. x = torch.tensor([[1], [1], [1], [1]], dtype=torch.float)  # N x emb(in)
  11. # 输入网络
  12. x = conv(x, edge_index)
  13. print(x)

tensor([[0.4282, 2.2683], [0.2447, 1.2962], [0.2447, 1.2962], [0.2447, 1.2962]], grad_fn=)

可以看到，我们输入的特征向量的长度为1，输出的向量长度的特征为2，为什么特征向量的长度发生了改变？

三 消息传递过程

这一部分和PyT消息传递网络部分相似，只不过这里是具体针对GCN的实现。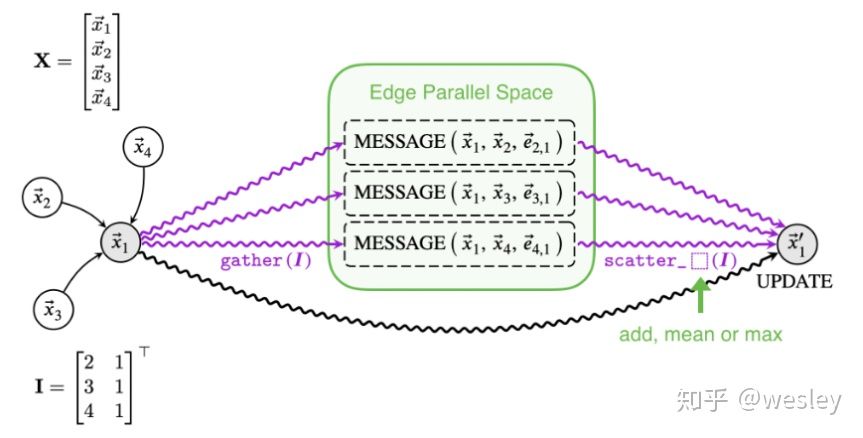
♠ PyT实现GCN - 图9
图2. 节点和节点消息传递过程
这个消息传递的过程是PyTorch Geometric中的内置代码的所实现的过程，首先是针对中心节点♠ PyT实现GCN - 图10和其邻边节点♠ PyT实现GCN - 图11，通过消息传递机制传递它们的信息，之后通过不同的聚合方式将每个邻边节点得到的特征联合起来。

图2中的左半部分对应的是下面的公式2：
♠ PyT实现GCN - 图12

我们的邻边矩阵的特征首先通过一个权重矩阵♠ PyT实现GCN - 图13进行改变，就类似于线性变换层的操作一样，所以我们的输出的维度out_channels会发生改变：
♠ PyT实现GCN - 图14
之后通过度degree进行归一化，然后再进行整合。

现在使用矩阵的变化形式来描述整个过程：
♠ PyT实现GCN - 图15

其中的♠ PyT实现GCN - 图16表示带有自循环（♠ PyT实现GCN - 图17）的邻接矩阵，其中的♠ PyT实现GCN - 图18表示度矩阵（用于归一化）

四 PyT的GCN过程

1. 初始化参数

首先是初始化相关的参数♠ PyT实现GCN - 图19

  1. # 做类似于Linear层的操作，改变输出的维度
  2. self.weight = torch.nn.Parameter(torch.Tensor(in_channels, out_channels))
  3. # 添加最后Update部分的bias
  4. self.bias = torch.nn.Parameter(torch.Tensor(out_channels))

2. 改变输出维度

我们在上述调用API接口时候，可以看到输出变为2，所以这里我们将它手动实现，看看它是怎么改变的

  1. # N x emb(out) = N x emb(in) @ emb(in) x emb(out)
  2. x = torch.matmul(x, self.weight)

3. 实现自循环邻接矩阵♠ PyT实现GCN - 图20

  1. def add_self_loops(edge_index, num_nodes=None):
  2.     loop_index = torch.arange(0, num_nodes, dtype=torch.long,
  3.                               device=edge_index.device)
  4.     loop_index = loop_index.unsqueeze(0).repeat(2, 1)
  5.     edge_index = torch.cat([edge_index, loop_index], dim=1)
  7.     return edge_index
  10. edge_index = add_self_loops(edge_index, x.size(0))  # 2 x (E+N)

4. 计算归一化

现在实现通过degree矩阵实现归一化：

  1. edge_weight = torch.ones((edge_index.size(1),),
  2.                           dtype=x.dtype,
  3.                           device=edge_index.device)  # [E+N]
  4. row, col = edge_index  # [E+N], [E+N]
  5. deg = scatter_add(edge_weight, row, dim=0, dim_size=x.size(0))  # [N]
  6. deg_inv_sqrt = deg.pow(-0.5)  # [N]
  7. deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0  # [N]  #same to use masked_fill_
  8. norm = deg_inv_sqrt[row] * edge_weight * deg_inv_sqrt[col]  # [E+N]

5. 节点消息传播

计算完上述的矩阵以后，就需要将这一层的节点消息传递到下一层

  1. self.propagate(edge_index, x=x, norm=norm)  # 2 x (E+N), 4 x emb(out), [E+N]

之后，归一化节点的特征：

  1. def message(self, x_j, norm):
  2.     return norm.view(-1, 1) * x_j

之后，将得到的特征进行聚合，在PyT中，使用的是scatter函数，这个函数重新写一篇来看一下PyT中的scatter函数是怎么实现聚合的。

6. Update层

在图2中，我们可以看到最后有一个Update，就是对整合好的邻边节点的特征是否添加bias

  1. def update(self, aggr_out):
  2.     if self.bias is not None:
  3.         return aggr_out + self.bias
  4.     else:
  5.         return aggr_out

五 自写GCN的实现

将四中的6个步骤写成一个类

  1. import torch
  2. from torch_scatter import scatter_add
  3. from torch_geometric.nn import MessagePassing
  4. import math
  7. def glorot(tensor):
  8.     if tensor is not None:
  9.         stdv = math.sqrt(6.0 / (tensor.size(-2) + tensor.size(-1)))
  10.         tensor.data.uniform_(-stdv, stdv)
  12. def zeros(tensor):
  13.     if tensor is not None:
  14.         tensor.data.fill_(0)
  16. def add_self_loops(edge_index, num_nodes=None):
  17.     print("Begin self_loops")
  18.     loop_index = torch.arange(0, num_nodes, dtype=torch.long,
  19.                               device=edge_index.device)
  20.     print(loop_index)
  21.     loop_index = loop_index.unsqueeze(0).repeat(2, 1)
  22.     print(loop_index)
  24.     edge_index = torch.cat([edge_index, loop_index], dim=1)
  25.     print(edge_index)
  26.     print("End self_loops")
  28.     return edge_index
  31. class GCNConv(MessagePassing):
  32.     def __init__(self, in_channels, out_channels, bias=True):
  33.         super(GCNConv, self).__init__(aggr='add')  # "Add" aggregation.
  34.         # super(GCNConv, self).__init__(aggr='max')  # "Max" aggregation.
  36.         self.weight = torch.nn.Parameter(torch.Tensor(in_channels, out_channels))
  38.         if bias:
  39.             self.bias = torch.nn.Parameter(torch.Tensor(out_channels))
  40.         else:
  41.             self.register_parameter('bias', None)
  43.         self.reset_parameters()
  45.     def reset_parameters(self):
  46.         glorot(self.weight)
  47.         zeros(self.bias)
  49.     def forward(self, x, edge_index):
  50.         # 1. Linearly transform node feature matrix  (XΘ)
  51.         x = torch.matmul(x, self.weight)  # N x emb(out) = N x emb(in) @ emb(in) x emb(out)
  52.         print('x', x)
  54.         # 2. Add self-loops to the adjacency matrix   (A' = A + I)
  55.         edge_index = add_self_loops(edge_index, x.size(0))    # 2 x (E+N)
  56.         print('edge_index', edge_index)
  58.         # 3. Compute normalization  ( D^(-0.5) A D^(-0.5) )
  59.         edge_weight = torch.ones((edge_index.size(1),),
  60.                                  dtype=x.dtype,
  61.                                  device=edge_index.device)  # [E+N]
  62.         print('edge_weight', edge_weight)
  63.         row, col = edge_index  # [E+N], [E+N]
  64.         print("row", row)
  65.         print("col", col)
  66.         deg = scatter_add(edge_weight, row, dim=0, dim_size=x.size(0))  # [N]
  67.         print("deg", deg)
  68.         deg_inv_sqrt = deg.pow(-0.5)  # [N]
  69.         deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0  # [N]  # same to use masked_fill_
  70.         norm = deg_inv_sqrt[row] * edge_weight * deg_inv_sqrt[col]  # [E+N]
  71.         print('norm', norm)
  73.         # 4. Start propagating messages
  74.         return self.propagate(edge_index, x=x, norm=norm)  # 2 x (E+N), N x emb(out), [E+N]
  76.     def message(self, x_j, norm):  # 4.1 Normalize node features.
  77.         # x_j: after linear x and expand edge  (N+E) x emb(out) = N x emb(in) @ emb(in) x emb(out) (+) E x emb(out)
  78.         print('x_j', x_j)
  79.         print('norm', norm)
  80.         print(f'Norm*x_j: {norm.view(-1, 1) * x_j}')
  81.         return norm.view(-1, 1) * x_j  # (N+E) x emb(out)  
  82.         # return: each row is norm(embedding) vector for each edge_index pair
  84.     def update(self, aggr_out):  # 4.2 Return node embeddings
  85.         print('aggr_out', aggr_out)  # N x emb(out)
  86.         # for Node 0: Based on the directed graph, Node 0 gets message from three edges and one self_loop
  87.         # for Node 1, 2, 3: since they do not get any message from others, so only self_loop
  88.         if self.bias is not None:
  89.             return aggr_out + self.bias
  90.         else:
  91.             return aggr_out
  95. torch.manual_seed(0)
  97. edge_index = torch.tensor([[1, 2, 3], [0, 0, 0]], dtype=torch.long)   # 2 x E
  98. x = torch.tensor([[1], [1], [1], [1]], dtype=torch.float)   # N x emb(in)
  99. print('x', x)
  100. print('edge_index', edge_index)
  102. # from 1 dim -> 2 dim
  103. conv = GCNConv(1, 2)   # emb(in), emb(out)
  105. # forward
  106. x = conv(x, edge_index)
  107. print(x)  # N x emb(out)    =aggr_out

六 原文链接

https://zhuanlan.zhihu.com/p/208019993