一、官方代码

在看PyTorch的官方文档的时候，看到了卷积网络的定义代码

class Net(nn.module):
    def __init__(self):
        super(Net, self).__init__()
        #1 input image channel,  6 output channels, 3x3 square convolution
        #kernel
        #卷积层
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        #an affine operation: y = W.x + b
        #全连接层
        self.fc1 = nn.Linear(16 * 6 * 6, 120) #6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
     def forward(self, x):
        #Max pooling over a(2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        #If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x =self.fc3(x)
        return x
    def num_flat_features(self, x):
        sieze = x.size()[1:]    #all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
         return num_features
net = Net()
print(net)

二、图像识别过程

从上面的代码中，可以得到，图像的识别过程为：

前向过程：

输入->卷积(conv1)->池化(max_pool2d)->卷积(conv2)->池化(max_pool2d)->Linear函数卷积->ReLU激活->Linear函数卷积->ReLU激活->Linear函数卷积->一次输出

就像下面这个图展示的样子

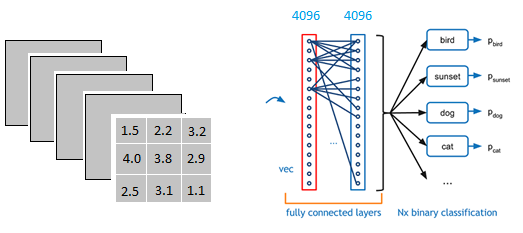
但是我们卷积完以后是矩阵形式的数据，而全连接层的数据是向量，如下图所示，这个过程是怎么进行的？

而且为什么要这么做？分割线在此，分割线以下的就是知乎博客里的解答了。

三、关于全连接的解惑

以上图为例，我们仔细看上图全连接层的结构，全连接层的每一层是由许多神经元组成的（1x4096）的平铺结构，上图不明显，我们看下图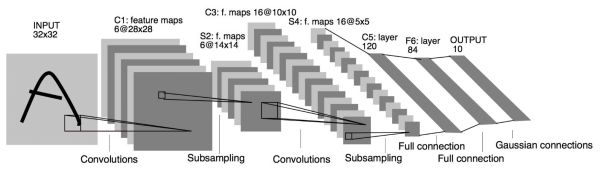

注：上图和我们要做的运算无联系，并且不考虑激活函数和bias

当我第一次看到这个全连接层，我的第一个问题是：

它是怎么样吧3x3x5的输出，转换成1x4096的形式：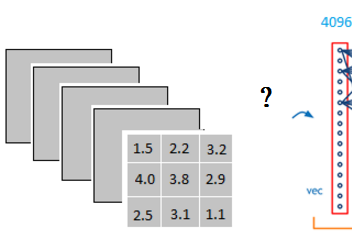

很简单，可以理解为中间做了一个卷积

由上图我们可知，使用1个3x3x5大小的filter与3x3x5大小的输出卷积，得到的就是全连接层(Fully connected layer)的一个神经元的输出，这个输出就是一个值。

所以，当我们使用4096个3x3x5大小的filter与3x3x5大小的输出卷积，得到的就是4096个值。所以我们实际上就是使用3x3x5x4096的卷积层去卷积激活函数的输出。

为什么这么做？

把分布式特征(representation)映射到样本标记空间，即：把特征(representation)整合到一起，输出为一个值。So, 为什么要整合？能够大大减少特征位置对分类带来的影响。

听不懂吧，我也听不懂，直观地感受下，举个例子：

这个图的意思就是：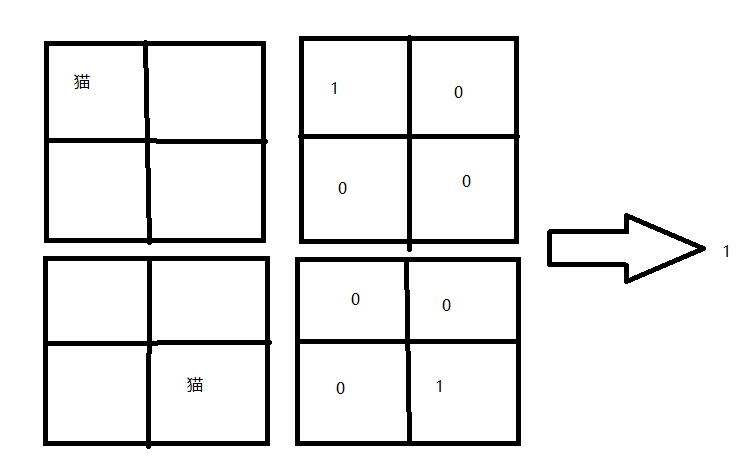

从上图我们可以看出，猫虽然在不同的位置，但是输出的feature值是相同的；但是对于电脑来说，我们是要利用它来进行分类的，特征值相同，但是特征位置不同的话可能有不一样的分类结果。

这时全连接filter的作用就相当于：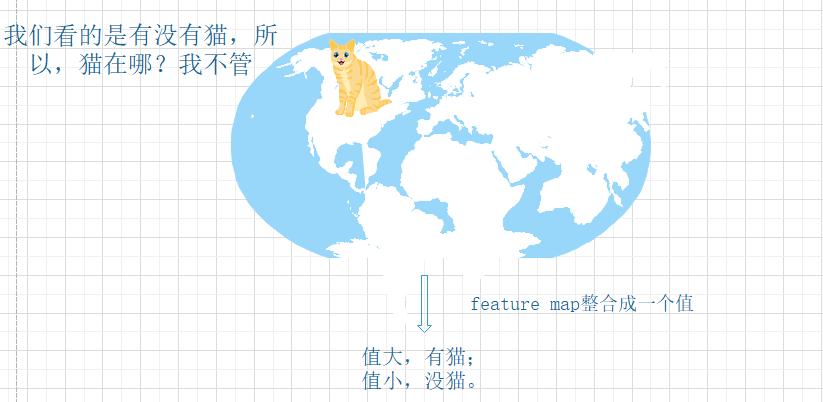

至此，大大增强了鲁棒性。但是，有得必有失，因为忽略了位置信息，所以全连接层不适合用于在方位上找Pattern的任务，比如segmentation。

从上面的图片中，我们可以看到全连接层有3个

为什么全连接层大多都是2层以上呢？

提到拟合这个话题，最基本的就是泰勒公式了，因为任何的函数都可以用多项式函数去拟合，我们这里的全连接层中一层的神经元就可以看成一个多项式。

我们用许多神经元去拟合数据分布，但是只用一层全连接层(fully connected layer)有时候没有办法很好地去解决非线性问题，而如果有两层及以上fully connected layer就可以很好地解决非线性问题了。

我们继续从猫这个例子来直观地理解。

我们都知道，全连接层之前的作用是特征提取，全连接层的作用是分类。我们现在的任务是去区别一张图片是不是猫：

假设这个神经网络模型已经训练完了，全连接层已经知道了这些特征：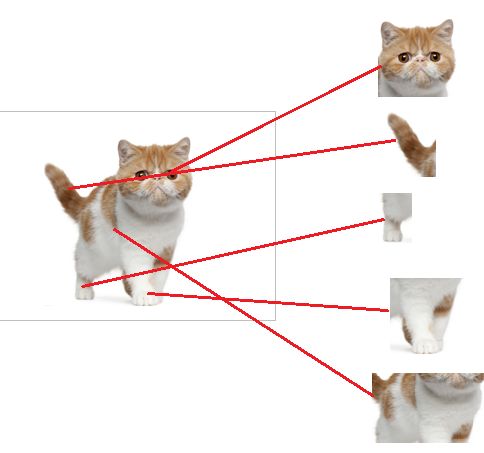

当我们得到以上特征的时候，我们就可以判断出这个东西是猫，因为全连接层的作用主要就是实现分类，从下图，我们可以看出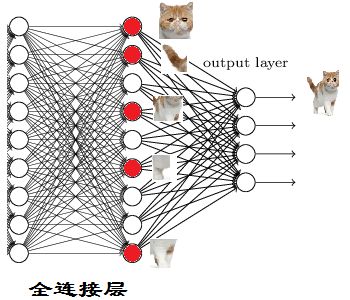

红色的神经元表示这个特征被找到了（激活了），同一层的其他神经元吗，要么猫的特征不明显，要么没找到。当我们把这些找到的特征组合在一起时，发和最符合要求的是猫。

OK，这时我们认为这就是猫。

然后，我们在往前走一层，我们现在要对子特征分类，也就是对猫头、猫尾巴、猫腿等进行分类，比如我们现在要把猫头找出来。

猫头有这么些个特征，于是我们下一步的任务，就是把猫头的这么些子特征找到，比如眼睛啊，耳朵啊。

道理和区别猫一样，当我们找到这些特征，神经元就被激活了（上图红色圆圈）。这细节特征又是怎么来的？就是从前面的卷积层，下采样层来的

至此，关于全连接层的信息就简单介绍完了

四、更多关于全连接层

全连接层参数特多（可占整个网络参数80%左右），近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代全连接层来融合学到的深度特征。

需要指出的是，用GAP替代FC的网络通常有较好的预测性能

于是还出现了Fully Convolutional Networks for Semantic Segmentation

另外，还有一些问题：

4.1 全连接层对模型的影响？

首先我们明白全连接层的组成如下：

二层全连接层结构
那么全连接层对模型影响参数就是三个：

1. 全接解层的总层数（长度）
2. 单个全连接层的神经元数（宽度）
3. 激活函数

首先我们要明白激活函数的作用是：增加模型的非线性表达能力，更详细的请去：CNN入门讲解：什么是激活函数（Activation Function）

4.2 参数改变带来的影响

如果全连接层宽度不变，增加长度：

• 优点：神经元个数增加，模型复杂度提升；全连接层数加深，模型非线性表达能力提高。理论上都可以提高模型的学习能力
• 缺点：学习能力太好容易造成过拟合

如果全连接层长度不变，增加宽度：

• 优点：神经元个数增加，模型复杂度提升。理论上可以提高模型的学习能力。
• 缺点：运算时间增加，效率变低

4.3 如何判断模型学习能力

看测试曲线以及 验证曲线，在其他条件理想的情况下，如果测试曲线高， 验证曲线低，也就是过拟合 了，可以尝试去减少层数或者参数。如果测试曲线低，说明模型学的不好，可以尝试增加参数或者层数。至于是增加长度和宽度，这个又要根据实际情况来考虑了。

PS：很多时候我们设计一个网络模型，不光考虑准确率，也常常得在Accuracy/Efficiency 里寻找一个好的平衡点。