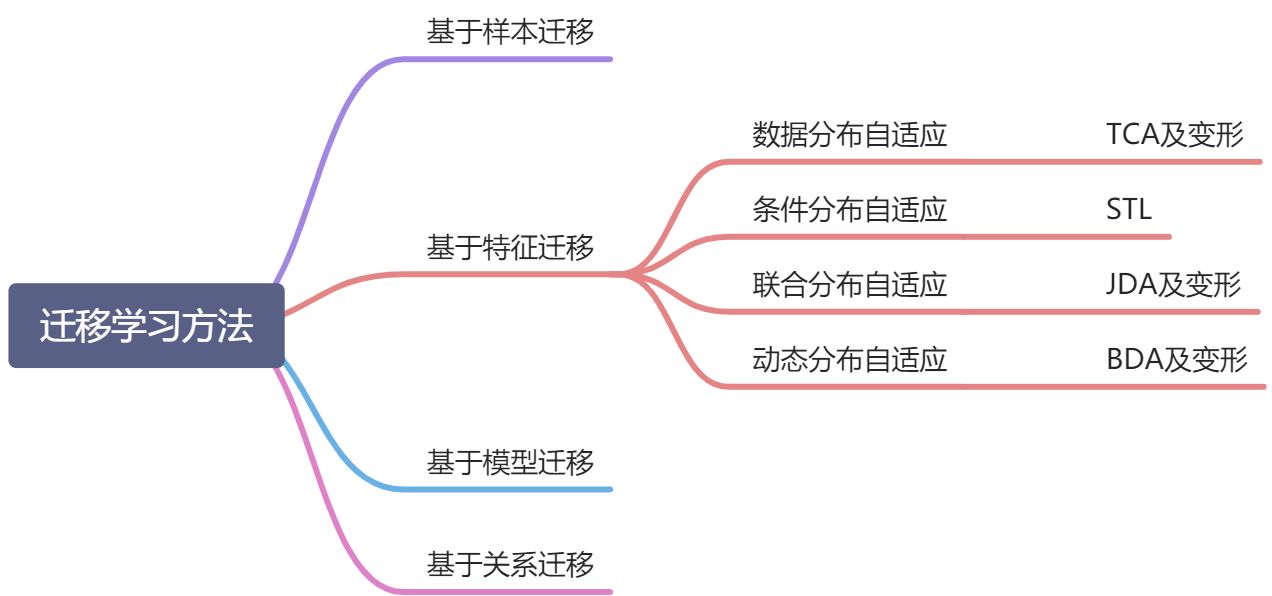
一、基于样本迁移

增加源域中与目标域有关部分的数据集的权重，关于这方面的方法有：

• TrAdaboost方法
• 传递迁移学习TTL方法
• 远域迁移学习DDTL

二、基于特征的迁移

基于特征的迁移方法是指通过特征变换的方式互相迁移，来减少源域和目标域之间的差距（数据分布自适应） || 将源域和目标域的数据特征变换到统一特征空间中（特征选择）。

2.1 数据分布自适应

边缘分布自适应方法（Marginal Distribution Adaptation）的目标是减小源域和目标域的边缘概率分布的距离，从而完成迁移学习。


%20%5Capprox%20%5C%7C%20P(%5Cmathrm%7Bxs%7D-P(%5Cmathrm%7Bx_t%7D))%20%5C%7C%0A#card=math&code=%5Cmathrm%7BDISTANCE%7D%28%5Cmathcal%7BD%7D%7Bs%7D%2C%20%5Cmathcal%7BD%7D_%7Bt%7D%29%20%5Capprox%20%5C%7C%20P%28%5Cmathrm%7Bx_s%7D-P%28%5Cmathrm%7Bx_t%7D%29%29%20%5C%7C%0A&id=NvjRQ)

边缘分布自适应对应的变化如图所示：

做的一些相关的工作如下所示：

TCA 方法是迁移学习领域一个经典的方法，之后的许多研究工作都以 TCA 为基础。我们列举部分如下：

• ACA (Adapting Component Analysis) [Dorri and Ghodsi, 2012]: 在 TCA 中加入HSIC
• DTMKL (Domain Transfer Multiple Kernel Learning) [Duan et al., 2012]: 在 TCA中加入了 MK-MMD，用了新的求解方式
• TJM (Transfer Joint Matching) [Long et al., 2014b]: 在优化目标中同时进行边缘分布自适应和源域样本选择
• DDC (Deep Domain Confusion) [Tzeng et al., 2014]: 将 MMD 度量加入了深度网络特征层的 loss 中 (我们将会在深度迁移学习中介绍此工作)
• DAN(Deep Adaptation Network) [Long et al., 2015a]: 扩展了 DDC 的工作，将 MMD换成了 MK-MMD，并且进行多层 loss 计算 (我们将会在深度迁移学习中介绍此工作)
• DME(Distribution Matching Embedding): 先计算变换矩阵，再进行特征映射 (与TCA 顺序相反)
• CMD (Central Moment Matching) [Zellinger et al., 2017]: MMD 着眼于一阶，此工作将 MMD 推广到了多阶

2.2 条件分布自适应

条件分布自适应方法 (Conditional Distribution Adaptation) 的目标是减小源域和目标域的条件概率分布的距离，从而完成迁移学习。从形式上来说，条件分布自适应方法是用#card=math&code=P%28ys%7Cxs%29&id=LmJ1I) 和 #card=math&code=P%28yt%7Cxt%29&id=e4C5T) 之间的距离来近似两个领域之间的差异。即：

%20%5Capprox%20%5C%7CP(ys%7Cxs)%20%E2%88%92%20P(yt%7Cxt)%5C%7C%20%0A#card=math&code=%5Cmathrm%7BDISTANCE%7D%28%5Cmathcal%7BD%7D_s%2C%20%5Cmathcal%7BD%7D_t%29%20%5Capprox%20%5C%7CP%28ys%7Cxs%29%20%E2%88%92%20P%28yt%7Cxt%29%5C%7C%20%0A&id=nl1Oc)

目前条件分布自适应用到的方法是STL方法。

2.3 联合分布自适应

联合分布自适应方法 (Joint Distribution Adaptation) 的目标是减小源域和目标域的联合概率分布的距离，从而完成迁移学习。从形式上来说，联合分布自适应方法是用 #card=math&code=P%28xs%29&id=RvDVV) 和#card=math&code=P%28xt%29&id=B0glc) 之间的距离、以及 $P (ys|xs) $和 $P (yt|xt) $之间的距离来近似两个领域之间的差异。

%20%E2%89%88%20%5C%7CP%20(xs)%20%E2%88%92%20P(xt)%5C%7C%20%2B%20%5C%7CP(ys%7Cxs)%20%E2%88%92%20P%20(yt%7Cxt)%5C%7C%0A#card=math&code=%5Cmathrm%7BDISTANCE%7D%28%5Cmathcal%7BD%7D_s%2C%20%5Cmathcal%7BD%7D_t%29%20%E2%89%88%20%5C%7CP%20%28xs%29%20%E2%88%92%20P%28xt%29%5C%7C%20%2B%20%5C%7CP%28ys%7Cxs%29%20%E2%88%92%20P%20%28yt%7Cxt%29%5C%7C%0A&id=HSCsN)

就是将数据分布自适应的边缘概率和条件分布自适应条件概率相加，关于这方面的工作：

JDA方法是十分经典的迁移学习方法。后续的相关工作通过在 JDA 的基础上加入额外的损失项，使得迁移学习的效果得到了很大提升。我们在这里简要介绍一些基于 JDA 的相关工作。

• ARTL (Adaptation Regularization) [Long et al., 2014a]: 将 JDA 嵌入一个结构风险最小化框架中，用表示定理直接学习分类器
• VDA[Tahmoresnezhad and Hashemi, 2016]: 在 JDA 的优化目标中加入了类内距和类间距的计算
• Hsiao et al., 2016]: 在 JDA 的基础上加入结构不变性控制
• [Hou et al., 2015]：在 JDA 的基础上加入目标域的选择
• JGSA (Joint Geometrical and Statistical Alignment) [Zhang et al., 2017a]: 在 JDA的基础上加入类内距、类间距、标签持久化
• JAN (Joint Adaptation Network) [Long et al., 2017]: 提出了联合分布度量 JMMD，在深度网络中进行联合分布的优化

2.4 动态分布自适应

动态分布自适应是在上面联合分布自适应的基础上进行改进的，因为我们上面的联合分布自适应得到的距离是两个距离的和，所以得有一个合适的权重，针对不同的数据集要适当地改变这两个距离的权重大小，这个就类似于我们的深度学习中的正则化了。

关于这方面的工作有：

• BDA方法，改变距离为%20%5Capprox%20(1%20%E2%88%92%20%5Cmu)%5Ctimes%20%5Cmathrm%7BDISTANCE%7D(P(xs)%2C%20P%20(xt))%0A%2B%20%5Cmu%20%5Ctimes%20%5Cmathrm%7BDISTANCE%7D(P(ys%7Cxs)%2C%20P%20(yt%7Cxt))%0A#card=math&code=%5Cmathrm%7BDISTANCE%7D%28%5Cmathcal%7BD%7D_s%2C%20%5Cmathcal%7BD%7D_t%29%20%5Capprox%20%281%20%E2%88%92%20%5Cmu%29%5Ctimes%20%5Cmathrm%7BDISTANCE%7D%28P%28xs%29%2C%20P%20%28xt%29%29%0A%2B%20%5Cmu%20%5Ctimes%20%5Cmathrm%7BDISTANCE%7D%28P%28ys%7Cxs%29%2C%20P%20%28yt%7Cxt%29%29%0A&id=tpCDM)
  其中的平衡因子 µ 可以通过分别计算两个领域数据的整体和局部的 A-distance 近似给出。特别地，当 µ = 0 时，方法退化为 TCA；当 µ = 0.5 时，方法退化为 JDA。
• BDA 方法是首次给出边缘分布和条件分布的定量估计。然而，其并未解决平衡因子的精确计算问题。最近，作者扩展了 BDA 方法，提出了一个更具普适性的动态迁移框架DDA(Dynamic Distribution Adaptation) [Wang et al., 2019] 来解决值的精确估计问题。
• 作者分别提出了基于流形学习的动态迁移方法MEDA(Manifold Embedded Distribution Alignment) [Wang et al., 2018b] 和基于深度学习的动态迁移方法DDAN (Deep Dynamic Adaptation Network) [Wang et al., 2019] 来进行学习。
• 最近，作者在 [Yu et al., 2019] 中将 DDA 的概念进一步扩展到了对抗网络中，证明了对抗网络中同样存在边缘分布和条件分布不匹配的问题。作者提出一个动态对抗适配网络DAAN (Dynamic Adversarial Adaptation Networks) 来解决对抗网络中的动态分布适配问题，取得了当前的最好效果。
  

2.5 边缘概率分布和条件概率分布具体指的是什么

这部分引自东哥的回答

边缘概率就是#card=math&code=P%28x%29&id=B7EqL)，指的是产生数据的分布；条件概率是#card=math&code=P%28y%7Cx%29&id=NCMBl)，就是数据和标签之间的后验概率分布，和学习任务有关。

#card=math&code=P%28x%29&id=xdcDM)不同是说数据产生的机制不同。比如：从不同光照背景下照相机照出来的图像和视频，不同的个体产生的行为的数据，不同的主题使用到的文本特征。

#card=math&code=P%28y%7Cx%29&id=uXBNL)不同是说即使数据来自于同一个分布（边缘概率#card=math&code=P%28x%29&id=D57TB)相同，但是在涉及到具体任务，如分类、回归等任务时，其概率也是不同的）。比如，都是来自一个人的脑电数据，但是在兴奋刺激和悲伤刺激下的条件概率分布#card=math&code=P%28y%7Cx%29&id=m3Kg8)时不相同的。

三、基于模型迁移

从源域数据和目标域数据中找到它们共享的参数信息，从而实现迁移。所以，这里有一个假设条件为：源域中的数据与目标域中的数据可以共享一些模型的参数。

四、基于关系迁移

基于关系的迁移，主要是根据目标域和源域之间的关系来进行迁移的，找到类似的关系