原文链接
这个例子是用来展示如何训练一个卷积神经网络来预测手写字的旋转角度，卷积神经网络对于深度学来说是很重要的，对于分析图像数据来说非常合适。你可以用卷积神经网络来对图像进行分类（离散的）和回归（连续的），预测图像的角度和距离，可以在这个网络的最后加上一个回归层。
这个例子构建了一个卷积神经网络架构，训练一个神经网络，使用这个训练好的神经网络去预测旋转手写字体的旋转角度。
同样地，可以使用 imrotate（图像处理工具箱）来旋转这些图像，使用 boxplot（统计和机器学习工具箱）创建一个残差箱型图。

加载数据

使用 digitTrain4DArrayData和 digitTest4DArrayData加载训练和验证图片成为4维矩阵。最后的输出 YTrain和 YValidation是旋转的角度。训练集和验证集各含5000张图片。

[XTrain, ~, YTrain] = digitTrain4DArrayData;
[XValidation, ~, YValidation] = digitTest4DArrayData;

使用 imshow随机展示20张训练图片

numTrainImages = numel(YTrain);
figure
idx = randperm(numTrainImages, 20);
for i = 1:numel(idx)
    subplot(4, 5, i);
  imshow(XTrain(:, :, :, idx(i)));
end

♠ 训练用于回归的卷积神经网络 - 图1
图1. 随机展示训练的20张图

检查数据的归一化

当训练神经网络的时候，通常情况下，他都会帮你确认你的数据是否在网络所有阶段都已经归一化。归一化能够使得在使用梯度下降的时候更加平稳，并且能够加速这个过程。如果数据没有归一化的话，在训练过程的损失结果可能会变成NAN，网络的参数可能会发生偏差。最常用的归一化方式就是将所有的数据大小调到[0, 1]区间上，最终的平均值为0，方差为1，我们可以归一化的数据如下：

输入数据。在投入网络之前要进行归一化。在这个例子中，最终要归一化到[0, 1]。
每层的输出。你可以归一化每个卷积层和全连接层通过归一化层，在训练开始的时候，我们就会将数据归一化。如果我们的训练数据进行了归一化，那么最后的预测结果同样也要进行，否则会产生偏差。

将我们投入到网络中的结果分布画出，这个结果已经归一化到-45°-45°，所以这部分不需要进行归一化。

figure
histogram(YTrain)
axis tight
ylabel('Counts')
xlabel('Rotation Angle')

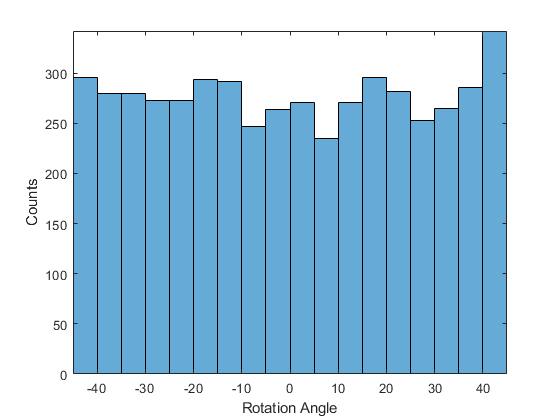
♠ 训练用于回归的卷积神经网络 - 图2
图2. 结果分布
通常情况下，我们的数据不是必须要归一化。但是，在这个例子中，我们最终要训练的是100*YTrain而不是YTrain，所以最终的结果可能很大变成NAN，最终的网络参数可能会发生偏差。
如果输入非常不均匀的话，也可以在训练之前使用非线性变化。

创建网络层(指定网络的大小)

为了解决回归问题，创建网络层+回归层，第一层是输入数据的大小和类型。我们的输出数据的大小为28×28×1.创建一个和训练图像一样大小的图像输入层。
网络的中间层定义了网络的核心结构，基本上我们的计算和学习都是在中间层进行的。
最后一层定义了输入出数据的大小和类型。对于回归问题，一个完全连接层必须要在最后的回归层之前，创建一个输出大小为1的全连接层和回归层。
将所有的连接层参数，放到一个矩阵中：

layers = [
imageInputLayer([28, 28, 1])
convolution2dLayer(3, 8, 'Padding', 'same')
batchNormalizationLayer
reluLayer
averagePooling2dLayer(2, 'Stride', 2)
convolution2dLayer(3, 16, 'Padding', 'same')
batchNormalizationLayer
reluLayer
averagePooling2dLayer(2, 'Stride', 2)
convolution2dLayer(3, 32, 'Padding', 'same')
batchNormalizationLayer
reluLayer
convolution2dLayer(3, 32, 'Padding', 'same')
batchNormalizationLayer
reluLayer
dropoutLayer(0.2)
fullyConnectedLayer(1)
regressionLayer
];

训练网络(指定网络的参数)

这部分主要是调整网络训练部分的参数，要训练30个epochs。设定最初的学习率是0.001并且在经历20个epochs后要减小学习率，在训练期间通过指定验证集和验证频率来监测网络的准确率。开启训练过程的画图，关掉命令行窗口的输出。

miniBatchSize = 128;
validationFrequencey = floor(numel(YTrain)/miniBatchSize);
options = trainingOptions(
                    'MiniBatchSize', miniBatchSize,...
          'MaxEpochs', 30, ...
          'InitialLearnRate', 1e-3, ...
          'LearnRateSchedule', 'piecewise', ...
          'LearnRateDropFactor', 0.1, ...
          'LearnRateDropPeriod', 20, ...
          'Shuffle', 'every-epoch', ...
          'ValidationData', {XValidation, YValidation}, ...
          'ValidationFrequency', validationFrequency, ...
          'Plots', 'training-progress', ...
          'Verbose', false
);

使用 trainNetwork创建训练网络，如果条件允许，我们还可以使用GPU来训练。

net = trainNetwork(XTrain, YTrain, layers, options);

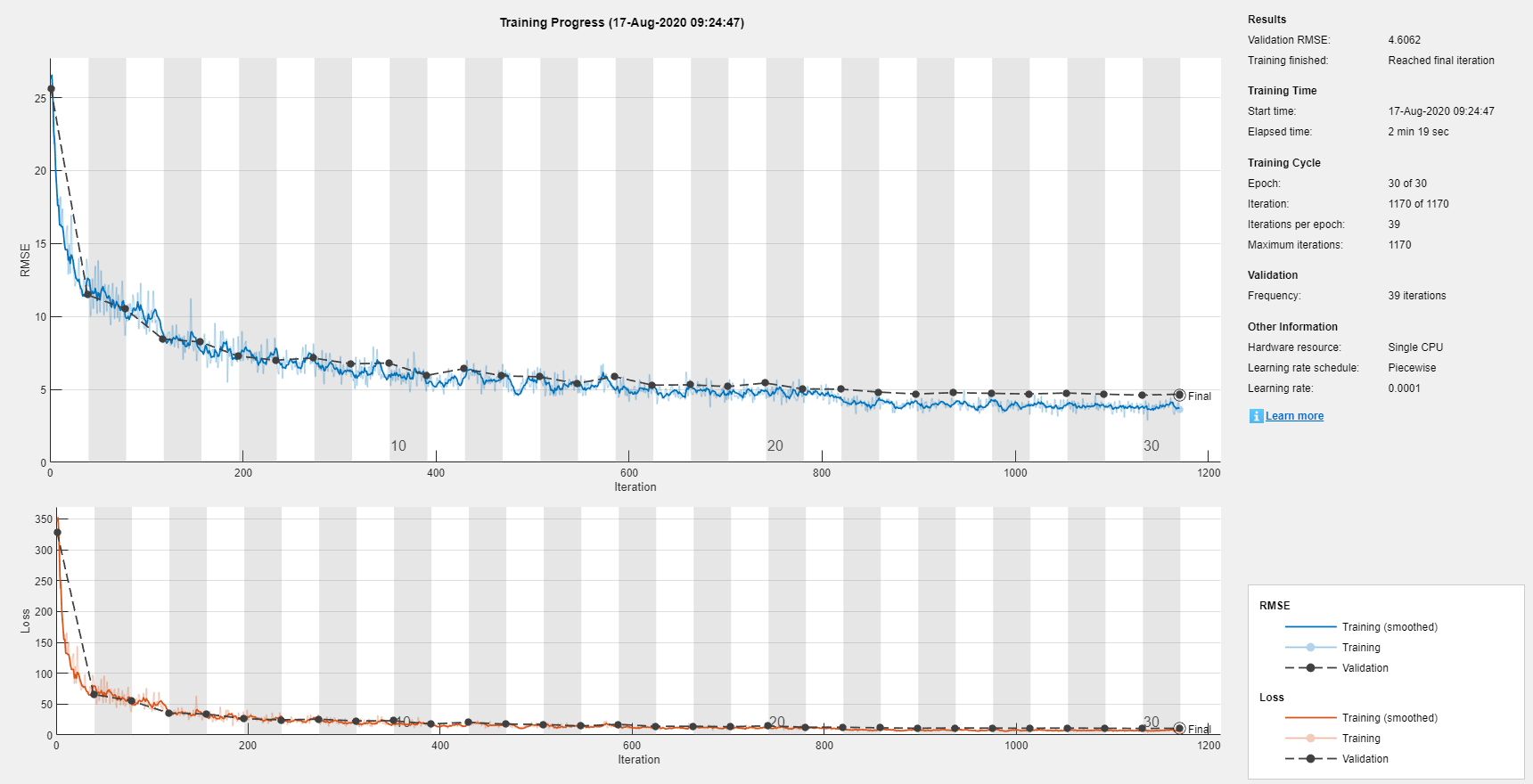
♠ 训练用于回归的卷积神经网络 - 图3
图3. 训练集
使用 Layers这个属性将我们训练好的网络结构net打印出来看一下

net.Layers

ans = 18×1 Layer array with layers:

 1   'imageinput'         Image Input           28×28×1 images with 'zerocenter' normalization
 2   'conv_1'             Convolution           8 3×3×1 convolutions with stride [1  1] and padding 'same'
 3   'batchnorm_1'        Batch Normalization   Batch normalization with 8 channels
 4   'relu_1'             ReLU                  ReLU
 5   'avgpool2d_1'        Average Pooling       2×2 average pooling with stride [2  2] and padding [0  0  0  0]
 6   'conv_2'             Convolution           16 3×3×8 convolutions with stride [1  1] and padding 'same'
 7   'batchnorm_2'        Batch Normalization   Batch normalization with 16 channels
 8   'relu_2'             ReLU                  ReLU
 9   'avgpool2d_2'        Average Pooling       2×2 average pooling with stride [2  2] and padding [0  0  0  0]
10   'conv_3'             Convolution           32 3×3×16 convolutions with stride [1  1] and padding 'same'
11   'batchnorm_3'        Batch Normalization   Batch normalization with 32 channels
12   'relu_3'             ReLU                  ReLU
13   'conv_4'             Convolution           32 3×3×32 convolutions with stride [1  1] and padding 'same'
14   'batchnorm_4'        Batch Normalization   Batch normalization with 32 channels
15   'relu_4'             ReLU                  ReLU
16   'dropout'            Dropout               20% dropout
17   'fc'                 Fully Connected       1 fully connected layer
18   'regressionoutput'   Regression Output     mean-squared-error with response 'Response'

验证集

通过分析验证数据集的准确率来看一下我们在训练集上训练好的网络的表现如何，使用 predict来预测我们验证的图片的旋转角度。

YPredicted = predict(net, XValidation);

分析结果

通过计算分析如下指标来衡量模型的表现：

设定可接受的最高误分率
我们预测的和真实的旋转角度之间的RMSE

计算误分类的错误率：

predictionError = YValidation - YPredicted;

计算在给定的可接受的预测错误率下的预测数量，设定阈值为10°，计算这个阈值下的预测准确率。

thr = 10;
numCorrect = sum(abs(predictionError) < thr);
numValidationImages = numel(YValidation);
accuracy = numCorrect/numValidationImages;

accuracy = 0.9690

计算预测的旋转角度和真实的旋转角度之间的RMSE

squares = predictionError.^2;
rmse = sqrt(mean(squares));

rmse = single
4.6062

预测结果可视化

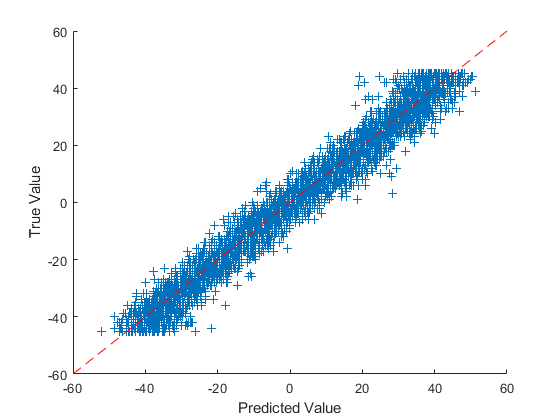
我们使用一个散点图来画出最后的预测结果，将真实值作为纵坐标，预测值作为横坐标，对角线是预测值==真实值：

figure
scatter(YPredicted, YValidation, '+');
xlabel('Predicted Value'); ylabel('True Value');
hold on 
plot([-60, 60], [-60, 60], 'r--');

♠ 训练用于回归的卷积神经网络 - 图4
图4. 预测结果可视化

矫正数字的旋转

可以使用图像处理工具箱的函数来矫正数字然后再展示。根据预测角度使用 imrotate函数旋转49°

idx = randperm(numValidationImages, 49);
for i = 1:numel(idx)
    image = XValidation(:, :, :, idx(i));
  predictedAngle = YPredicted(idx(i));
  imagesRotated(:, :, :, i) = imrotate(image, predictedAngle, 'bicubic', 'crop');
end

展示校正后的数字，可以使用 montage在一幅图中展示所有的数字：

figure;
subplot(1, 2, 1); montage(XValidation(:, :, :, idx)); title('Original');
subplot(1, 2, 2); montage(imagesRotated); title(Corrected)

♠ 训练用于回归的卷积神经网络 - 图5
图5. 原始图片和校正后的图片