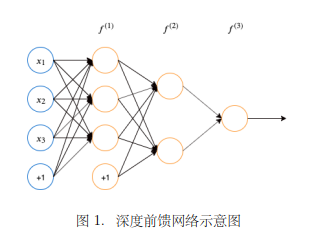
深度前馈网络
深度前馈网络(Deep Feedforward Network )也被称之为前馈神经网络(Feedforward Neural Network)或者多层感知机(Mutiplayer Perceptron)。是最典型的深度学习模型。
目标是拟合一个函数,如有一个分类器将输入
映射到输出类别
。深度前馈网将这个映射 定义为:
,把那个且学习这个参数
的值来得到最好的函数拟合。
前馈并不意味着网络中的信号不能反转,而是指网络拓扑中不能存在回路或环(反馈)。
深度前馈网络中信息从流入,通过中间
的计算,最后达到输出
。如图所示,假设由
这三个函数链式链接,这个链式连接可以表示为
,这种链式结构是神经网络最常用的结构。
被称为神经网络的第一层,第二层,也为网络的隐藏层(Hidden Layer),深度前馈网络最后一层
就是输出层(Output Layer)。这个链的长度就是神经网络的深度,输入向量的每个元素均视作一个神经元。
神经元模型
在介绍神经网络之前,我们先来看一下神经元的结构。
下图中 代表输入,
代表权重,b代表偏置,g代表非线性激活函数。
叫做带权输入,a叫做激活值,是神经元的输出。

神经网络的结构
前馈神经网络之所以被称为网络(network),是因为它们通常用许多不同函数复合在一起来表示。该模型与一个有向无环图相关联,而图描述了函数是如何复合在一起的。
我们以下图为例子说明神经网络的结构。神经网络分为输入层,隐藏层和输出层。前馈网络最前面的层称作输入层,最后一层称作输出层,中间既不是输入也不是输出的层叫做隐藏层。
下图是一个3层的神经网络,输入层不计入层数。神经网络的层数称为模型的深度,正是因为这个术语才出现了“深度学习”这个名字。每一层的节点都代表一个神经元(neuron),每层的单元数代表了模型的宽度。
神经网络的标记
我们首先以神经元为基本单位给出权重,偏置,带权输入,激活值的表示。然后以神经元的层为单位给出其矩阵表示。最后我们给出实际软件中使用的表示方法,这样的表示能够帮助我们处理多个输入向量。
单个神经元角度
我们首先给出网络中权重的清晰定义。我们使用 表示从
的
个神经元到
层的
个神经元的连接上的权重。例如下图给出了网络中第二层的第四个神经元到第三层的第二个神经元的连接上的权重:

我们对网络的偏置,激活值也会使用类似的表示。显式的,我们使 表示在
层的第
个神经元的偏置,使用
表示
层第
个神经元的激活值,
表示
层第
个神经元的激活函数的带权输入。下面的图清楚地解释了这样表示的含义:

有了这些表示, 层的第
个神经元的激活值
就和
层的激活值通过方程关联起来:
层的角度(单个输入样本)
 代表神经网络的第  层。  代表第  层神经元的个数。<br />我们对每一层  都定义**权重矩阵** ,偏置向量  ,带权输入向量  ,激活值向量 。<br /><br /> 是第  行第  列的元素。<br /> 的大小是 <br /> , ,<br />  的大小都是 <br />我们将**前向传播公式**写为如下矩阵形式:<br /><br />
多个样本的表示
当我们像让多个样本同时在网络中计算时,权重和偏置的表示方式没有变化。带权输入和激活值会有一些变化。我们假设同时输入的样本数为 ,对于第
个样本我们用上标
标记。
和
的不同列代表不同样本在该层的带权输入、激活值。
,shape=
, shape=
前向传播公式如下:
非线性激活函数
sigmoid函数

导数:
sigmoid函数在a接近0或者1时,函数的导数很小(接近0),会使模型收敛速度变慢。
我们一般不使用sigmoid函数,只在以下两种情况时使用:
- 1.二分类的时候,输出层使用
- 2.需要输出值在0到1之间,输出层使用
tanh函数
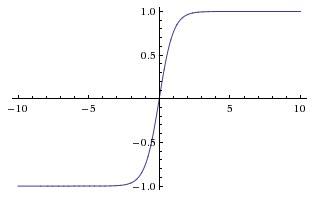
tanh函数和sigmoid函数的关系。。
导数:
tanh几乎在任何情况下效果都比sigmoid要好。tanh函数的值在-1和1之间,输出的结果的平均值为0。tanh函数和sigmoid函数的共同缺点是在z接近无穷大或无穷小时,这两个函数的导数也就是梯度变得非常小,此时梯度下降的速度也会变得非常慢。ReLu函数
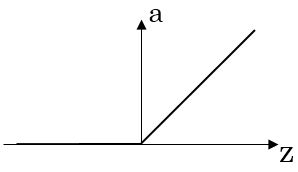
导数:
ReLU函数是非线性激活函数的默认选择,如果你不知道该选择哪个激活函数,ReLU很可能是个好的选择。
当z大于0时,ReLU的导数一直为1,所以采用ReLU函数作为激活函数时,随机梯度下降的收敛速度会比sigmoid及tanh快得多。Leaky ReLU函数
**
为什么需要非线性激活函数
如果没有非线性激活函数,得到的输出仅仅是输入的线性组合。这样多层的神经网络的模型复杂度就和单层神经网络一样了。
反向传播
下面是单个神经元的公式。
下面是向量化的公式(单个样本)。
最后我们给出同时输入多个样本时的公式,也是我们在编写程序时使用的公式。
具体实现
具体实现时,可以按照下图的流程和我们得到的公式进行前向和反向传播。这里就不详细说明了。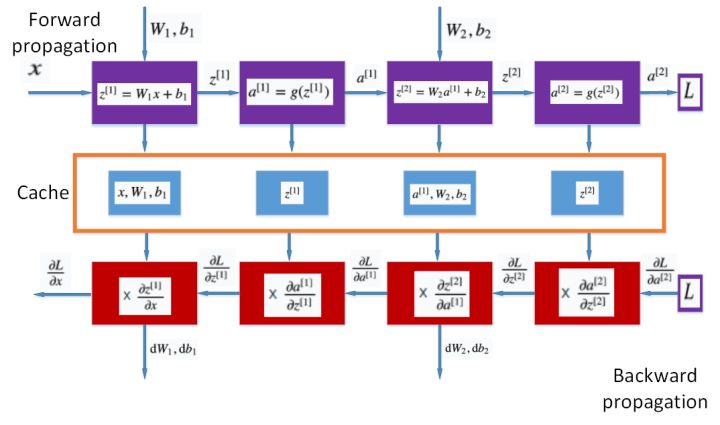
神经网络与神经科学
这些网络之所以被称为神经网络,是因为它们或多或少地受到神经科学的启发。然而,现代神经网络研究受到更多的是来自数学和工程学科的指引,并且神经网络的目标并不是完美的给大脑建模。我们最好将前馈神经网络想成是为了实现统计泛化而设计出的函数近似机,它偶尔从我们了解的大脑中提取灵感,但并不是大脑功能的模型。