原文链接

数据预处理

在训练神经网络前一般需要对数据进行预处理，一种重要的预处理手段是归一化处理。西面介绍归一化的处理的原理和方法。

什么是归一化？

数据归一化，就是将数据映射到[0,1]或者[-1,1]区间或者更小的空间，比如(0.1,0.9)。

为什么要归一化处理？

  • 1.输入数据的单位不一样，有些数据的范围可能特别大，导致的结果就是神经网络收敛慢、训练时间长。
  • 2.数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用可能会偏小。
  • 3.由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数，由于S形函数的值域限制在（0，1），也就是说神经网络的输出只能限制在（0，1），所以训练数据的输出就要归一化到[0,1]区间。

  • 4.S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数♠ BP神经网络的matlab实现 - 图1在参数♠ BP神经网络的matlab实现 - 图2时，♠ BP神经网络的matlab实现 - 图3与♠ BP神经网络的matlab实现 - 图4只相差0.0067

    归一化算法

    一种简单而又快速的归一化算法是线性转换算法。线性转换算法常见有两种形式：

  • ♠ BP神经网络的matlab实现 - 图5，其中♠ BP神经网络的matlab实现 - 图6是♠ BP神经网络的matlab实现 - 图7的最小值，♠ BP神经网络的matlab实现 - 图8是♠ BP神经网络的matlab实现 - 图9的最大值，输入向量是♠ BP神经网络的matlab实现 - 图10，归一化后的输出向量是♠ BP神经网络的matlab实现 - 图11。上式将数据归一化到♠ BP神经网络的matlab实现 - 图12区间，当激活函数采用S形函数时(值域为♠ BP神经网络的matlab实现 - 图13)时这条式子适用。

  • ♠ BP神经网络的matlab实现 - 图14这条公式将数据归一化到♠ BP神经网络的matlab实现 - 图15区间。当激活函数采用双极S形函数(值域为♠ BP神经网络的matlab实现 - 图16)时这条式子适用。

    matlab数据归一化处理函数

    matlab中归一化处理数据可以采用premnmx,postmnmx,tramnmx这三个函数。

  • premnmx函数

语法：[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
参数：
pn： p矩阵按行归一化后的矩阵
minp，maxp：p矩阵每一行的最小值，最大值
tn：t矩阵按行归一化后的矩阵
mint，maxt：t矩阵每一行的最小值，最大值
作用：将矩阵p，t归一化到[-1,1] ，主要用于归一化处理训练数据集。

  • postmnmx函数

语法： [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)
参数：
minp，maxp：premnmx函数计算的p矩阵每行的最小值，最大值
mint，maxt：premnmx函数计算的t矩阵每行的最小值，最大值
作用：将矩阵pn，tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。

  • tramnmx函数

语法：[pn] = tramnmx(p,minp,maxp)
参数：
minp，maxp：premnmx函数计算的矩阵的最小，最大值
pn：归一化后的矩阵
作用：主要用于归一化处理待分类的输入数据。

使用matlab实现神经网络

使用matlab建立前馈神经网络主要会使用到下面三个函数：
newff：前馈网络创建函数
train：训练一个神经网络
sim：使用网络进行仿真

newff函数

newff函数语法

newff函数参数列表有很多的可选参数，具体可以参考Matlab的帮助文档，这里介绍newff函数的一种简单的形式。
语法：net = newff ( A, B, {C} ,‘trainFun’)
参数：
A：一个n×2的矩阵，第i行元素为输入信号xi的最小值和最大值；
B：一个k维行向量，其元素为网络中各层节点数；
C：一个k维字符串行向量，每一分量为对应层神经元的激活函数；
trainFun ：为学习规则采用的训练算法。

常用的激活函数

常用的激活函数有：

  • 线性函数(Linear transfer function):

♠ BP神经网络的matlab实现 - 图17
该函数的字符串为’purelin’

  • 对数S形转移函数(Logarithmic sigmoid transfer function)

该函数的字符串为’logsig’

  • 双曲正切S形函数(Hyperbolic tangent sigmoid transfer function)

该函数的字符串为’tansig’

常见的训练函数

常见的训练函数有：

  • traingd:梯度下降BP训练函数(Gradient descent backpropagation)

  • traingdx:梯度下降自适应学习率训练函数

    网络配置函数

    一些重要的网络配置参数如下：

  • net.trainparam.goal ：神经网络训练的目标误差

  • net.trainparam.show ： 显示中间结果的周期
  • net.trainparam.epochs 　：最大迭代次数
  • net.trainParam.lr ： 学习率

    train函数

    网络训练学习函数。
    语法：[ net, tr, Y1, E ] = train( net, X, Y )
    参数：
    X：网络实际输入
    Y：网络应有输出
    tr：训练跟踪信息
    Y1：网络实际输出
    E：误差矩阵

    sim函数

    语法：Y=sim(net,X)
    参数：
    net：网络
    X：输入给网络的Ｋ×N矩阵，其中K为网络输入个数，N为数据样本数
    Y：输出矩阵Q×N，其中Q为网络输出个数

    Matlab BP网络实例

    我将Iris数据集分为2组，每组各75个样本，每组中每种花各有25个样本。其中一组作为以上程序的训练样本，另外一组作为检验样本。为了方便训练，将3类花分别编号为1，2，3 。
    　　使用这些数据训练一个4输入（分别对应4个特征），3输出（分别对应该样本属于某一品种的可能性大小）的前向网络。 ```matlab %读取训练数据 [f1,f2,f3,f4,class] = textread(‘trainData.txt’ , ‘%f%f%f%f%f’,150);

%特征值归一化 [input,minI,maxI] = premnmx( [f1 , f2 , f3 , f4 ]’) ;

%构造输出矩阵 s = length( class ) ; output = zeros( s , 3 ) ; for i = 1 : s output( i , class( i ) ) = 1 ; end

%创建神经网络 net = newff( minmax(input) , [10 3] , { ‘logsig’ ‘purelin’ } , ‘traingdx’ ) ;

%设置训练参数 net.trainparam.show = 50 ; net.trainparam.epochs = 500 ; net.trainparam.goal = 0.01 ; net.trainParam.lr = 0.01 ;

%开始训练 net = train( net, input , output’ ) ;

%读取测试数据 [t1 t2 t3 t4 c] = textread(‘testData.txt’ , ‘%f%f%f%f%f’,150);

%测试数据归一化 testInput = tramnmx ( [t1,t2,t3,t4]’ , minI, maxI ) ;

%仿真 Y = sim( net , testInput )

%统计识别正确率 [s1 , s2] = size( Y ) ; hitNum = 0 ; for i = 1 : s2 [m , Index] = max( Y( : , i ) ) ; if( Index == c(i) ) hitNum = hitNum + 1 ; end end sprintf(‘识别率是 %3.3f%%’,100 * hitNum / s2 )

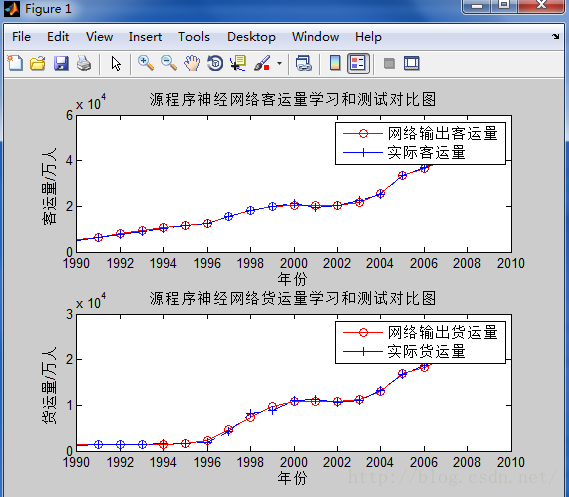
  1. <a name="97oaD"></a>
  2. ## **参数设置对神经网络性能的影响 **
  3. 我在实验中通过调整隐含层节点数，选择不通过的激活函数，设定不同的学习率，
  5. - **隐含层节点个数 **
  7. 　　隐含层节点的个数对于识别率的影响并不大，但是节点个数过多会增加运算量，使得训练较慢。
  9. - ** 激活函数的选择 **
  11.        激活函数无论对于识别率或收敛速度都有显著的影响。在逼近高次曲线时，S形函数精度比线性函数要高得多，但计算量也要大得多。
  13. - ** 学习率的选择 **
  15.        学习率影响着网络收敛的速度，以及网络能否收敛。学习率设置偏小可以保证网络收敛，但是收敛较慢。相反，学习率设置偏大则有可能使网络训练不收敛，影响识别效果。<br /> <br />[bpAnnIris.m](https://www.yuque.com/attachments/yuque/0/2020/m/1238812/1593155962629-5ddeb5f7-f10f-40c8-a21b-e4057850eeaa.m?_lake_card=%7B%22uid%22%3A%221593155963288-0%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2020%2Fm%2F1238812%2F1593155962629-5ddeb5f7-f10f-40c8-a21b-e4057850eeaa.m%22%2C%22name%22%3A%22bpAnnIris.m%22%2C%22size%22%3A997%2C%22type%22%3A%22application%2Fvnd.wolfram.mathematica.package%22%2C%22ext%22%3A%22m%22%2C%22progress%22%3A%7B%22percent%22%3A99%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%22baP1J%22%2C%22card%22%3A%22file%22%7D) [testData.txt](https://www.yuque.com/attachments/yuque/0/2020/txt/1238812/1593155731996-ec19fa78-c873-416e-8eb5-0d5b176a4705.txt?_lake_card=%7B%22uid%22%3A%221593155732643-0%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2020%2Ftxt%2F1238812%2F1593155731996-ec19fa78-c873-416e-8eb5-0d5b176a4705.txt%22%2C%22name%22%3A%22testData.txt%22%2C%22size%22%3A1349%2C%22type%22%3A%22text%2Fplain%22%2C%22ext%22%3A%22txt%22%2C%22progress%22%3A%7B%22percent%22%3A99%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%22SYD2y%22%2C%22card%22%3A%22file%22%7D)[trainData.txt](https://www.yuque.com/attachments/yuque/0/2020/txt/1238812/1593155740360-7682fa1a-3a13-4614-b5d1-ea10c11ade56.txt?_lake_card=%7B%22uid%22%3A%221593155740978-0%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2020%2Ftxt%2F1238812%2F1593155740360-7682fa1a-3a13-4614-b5d1-ea10c11ade56.txt%22%2C%22name%22%3A%22trainData.txt%22%2C%22size%22%3A1359%2C%22type%22%3A%22text%2Fplain%22%2C%22ext%22%3A%22txt%22%2C%22progress%22%3A%7B%22percent%22%3A99%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%22BYTye%22%2C%22card%22%3A%22file%22%7D)[totalData.txt](https://www.yuque.com/attachments/yuque/0/2020/txt/1238812/1593155747449-313d1f95-45ca-44e0-9742-5553917b78bc.txt?_lake_card=%7B%22uid%22%3A%221593155748083-0%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2020%2Ftxt%2F1238812%2F1593155747449-313d1f95-45ca-44e0-9742-5553917b78bc.txt%22%2C%22name%22%3A%22totalData.txt%22%2C%22size%22%3A2708%2C%22type%22%3A%22text%2Fplain%22%2C%22ext%22%3A%22txt%22%2C%22progress%22%3A%7B%22percent%22%3A99%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%22wqKwp%22%2C%22card%22%3A%22file%22%7D)[C#语言.zip](https://www.yuque.com/attachments/yuque/0/2020/zip/1238812/1593155945212-0af7832c-a9fa-4e34-9d0e-5a0d17e7668e.zip?_lake_card=%7B%22uid%22%3A%221593155945524-0%22%2C%22src%22%3A%22https%3A%2F%2Fwww.yuque.com%2Fattachments%2Fyuque%2F0%2F2020%2Fzip%2F1238812%2F1593155945212-0af7832c-a9fa-4e34-9d0e-5a0d17e7668e.zip%22%2C%22name%22%3A%22C%23%E8%AF%AD%E8%A8%80.zip%22%2C%22size%22%3A99315%2C%22type%22%3A%22application%2Fx-zip-compressed%22%2C%22ext%22%3A%22zip%22%2C%22progress%22%3A%7B%22percent%22%3A99%7D%2C%22status%22%3A%22done%22%2C%22percent%22%3A0%2C%22id%22%3A%22Aa16y%22%2C%22card%22%3A%22file%22%7D)
  17. ---
  19. [原文链接](https://blog.csdn.net/wyh7280/article/details/48250071?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase)<br />和以前的习惯一样，只举典例，然后给程序和运行结果进行说明。
  21. 问题背景是：
  23. 给定某地区20年的数据，6列，21行，第一列值为年份，第二列为人数，第三列为机动车数量，第四列为公路面积，第五列为公路客运量，第六列为公路货运量，这20年是1990年到2009年，现在给我们2010和2011年，第二、三和四列的数据，让我们用BP网络预测该地区2010年和2011年公路的客运量和公路货运量，也就是第五和六列的值。
  25. 问题背景详见《MATLAB在数学建模中的应用》卓金武第二版 134页 或者联系我。
  27. 其中，CUMCM 2006 B题 艾滋病治疗最佳停药时间的确定也可用此法，程序改改数据，还有神经网络输入输出层和隐含层的部分即可，详情多看书。
  29. 代码：
  30. ```matlab
  31. function main()
  32. clc             % 清屏
  33. clear all;      % 清除内存以便加快运算速度
  34. close all;      % 关闭当前所有figure图像
  35. warning off;    % 屏蔽没有必要的警告
  36. SamNum=20;      % 输入样本数量为20
  37. TestSamNum=20;  % 测试样本数量也是20
  38. ForcastSamNum=2;% 预测样本数量为2
  39. HiddenUnitNum=8;% 中间层隐节点数量取8
  40. InDim=3;        % 网络输入维度为3
  41. OutDim=2;       % 网络输出维度为2
  43. % 原始数据
  44. % 人数
  45. sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
  46. % 机动车数量
  47. sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1];
  48. sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79];
  49. % 公路客运量
  50. glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43467];
  51. % 公路货运量
  52. glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];
  54. p=[sqrs;sqjdcs;sqglmj];  % 输入数据矩阵
  55. t=[glkyl;glhyl];         % 目标数据矩阵
  56. [SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); % 原始样本对（输入和输出）初始化
  58. rand('state',sum(100*clock));   % 依据系统时钟种子产生随机数
  59. NoiseVar=0.01;                  % 噪声强度为0.01（添加噪声的目的是为了防止网络过度拟合）
  60. Noise=NoiseVar*randn(2,SamNum); % 生成噪声
  61. SamOut=tn+Noise;                % 将噪声添加到输出样本上
  63. TestSamIn=SamIn;                % 这里取输入样本与测试样本相同，因为样本容量偏少
  64. TestSanOut=SamOut;              % 也取输出样本与测试样本相同
  66. MaxEpochs=50000;                % 最多训练次数为50000
  67. lr=0.035;                       % 学习速率为0.035     
  68. E0=0.65*10^(-3);                % 目标误差为0.65*10^(-3)
  69. W1=0.5*rand(HiddenUnitNum,InDim)-0.1;% 初始化输入层与隐含层之间的权值
  70. B1=0.5*rand(HiddenUnitNum,1)-0.1;% 初始化输入层与隐含层之间的权值
  71. W2=0.5*rand(OutDim,HiddenUnitNum)-0.1;% 初始化输出层与隐含层之间的权值
  72. B2=0.5*rand(OutDim,1)-0.1;% 初始化输出层与隐含层之间的权值
  74. ErrHistory=[];  % 给中间变量预先占据内存
  75. for i=1:MaxEpochs          
  76.     HiddenOut=logsig(W1*SamIn+repmat(B1,1,SamNum)); % 隐含层网络输出
  77.     NetworkOut=W2*HiddenOut+repmat(B2,1,SamNum);   %输出层网络输出
  78.     Error=SamOut-NetworkOut;  % 实际输出与网络输出之差
  79.     SSE=sumsqr(Error);   % 能量函数(误差平方和)
  80.     ErrHistory=[ErrHistory SSE];
  81.     if SSE<E0,break,end  % 如果达到误差要求则跳出学习循环
  83.     % 以下6行是BP网络最核心的程序
  84.     % 它们是权值（阙值）依据能量函数负梯度下降原理所做的每一步动态调整
  85.     Delta2=Error;
  86.     Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);
  87.     % 对输出层与隐含层之间的权值和阙值进行修正
  88.     dW2=Delta2*HiddenOut';
  89.     dB2=Delta2*ones(SamNum,1);
  90.     % 对输入层与隐含层之间的权值和阙值进行修正
  91.     dW1=Delta1*SamIn';
  92.     dB1=Delta1*ones(SamNum,1);
  94.     W2=W2+lr*dW2;
  95.     B2=B2+lr*dB2;
  97.     W1=W1+lr*dW1;
  98.     B1=B1+lr*dB1;
  100. end
  102. HiddenOut=logsig(W1*SamIn+repmat(B1,1,TestSamNum));  % 隐含层输出最终结果
  103. NetworkOut=W2*HiddenOut+repmat(B2,1,TestSamNum);     % 输出层输出最终结果
  104. a=postmnmx(NetworkOut,mint,maxt);                    % 还原网络输出层的结果
  105. x=1990:2009;                                         % 时间轴刻度
  106. newk=a(1,:);                                         % 网络输出客运量
  107. newh=a(2,:);                                         % 网络输出货运量
  108. figure;
  109. subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+');  % 绘制公路客运量对比图
  110. legend('网络输出客运量','实际客运量');
  111. xlabel('年份'); ylabel('客运量/万人');
  112. title('源程序神经网络客运量学习和测试对比图');
  114. subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+');  % 绘制公路货运量对比图
  115. legend('网络输出货运量','实际货运量');
  116. xlabel('年份'); ylabel('货运量/万人');
  117. title('源程序神经网络货运量学习和测试对比图');
  119. % 利用训练好的数据进行预测
  120. % 当用训练好的网络对新数据pnew进行预测时，也应做相应的处理
  121. pnew=[73.39 75.55 
  122.     3.9635 4.0975
  123.     0.9880 1.0268];   % 2010年和2011年的相关数据
  124. pnewn=tramnmx(pnew,minp,maxp);  %利用原始输入数据的归一化参数对新数据进行归一化
  125. HiddenOut=logsig(W1*pnewn+repmat(B1,1,ForcastSamNum));  % 隐含层输出预测结果
  126. anewn=W2*HiddenOut+repmat(B2,1,ForcastSamNum);          % 输出层输出预测结果
  127. % 把网络预测得到的数据还原为原始的数量级
  128. format short
  129. anew=postmnmx(anewn,mint,maxt)

运行结果：
anew =
1.0e+004 *
4.1324 4.0941
2.1521 2.1440
实际样本与网络输出的对比图如下所示：
♠ BP神经网络的matlab实现 - 图18