作者：量子位
链接：https://www.zhihu.com/question/314879954/answer/638380202
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

搭建基本模块——神经元

在说神经网络之前，我们讨论一下神经元（Neurons），它是神经网络的基本单元。神经元先获得输入，然后执行某些数学运算后，再产生一个输出。比如一个2输入神经元的例子：

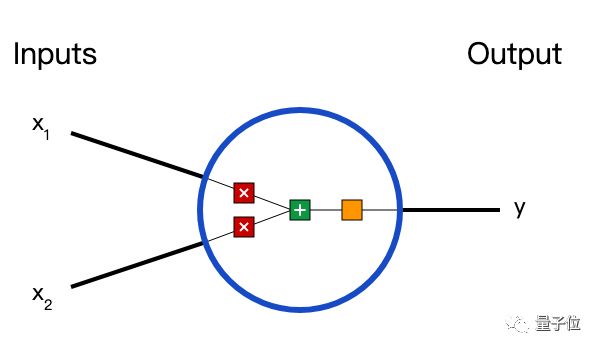
在这个神经元中，输入总共经历了3步数学运算，
先将两个输入乘以权重（weight）：


把两个结果想加，再加上一个偏置（bias）：

最后将它们经过激活函数（activation function）处理得到输出：

激活函数的作用是将无限制的输入转换为可预测形式的输出。一种常用的激活函数是sigmoid函数：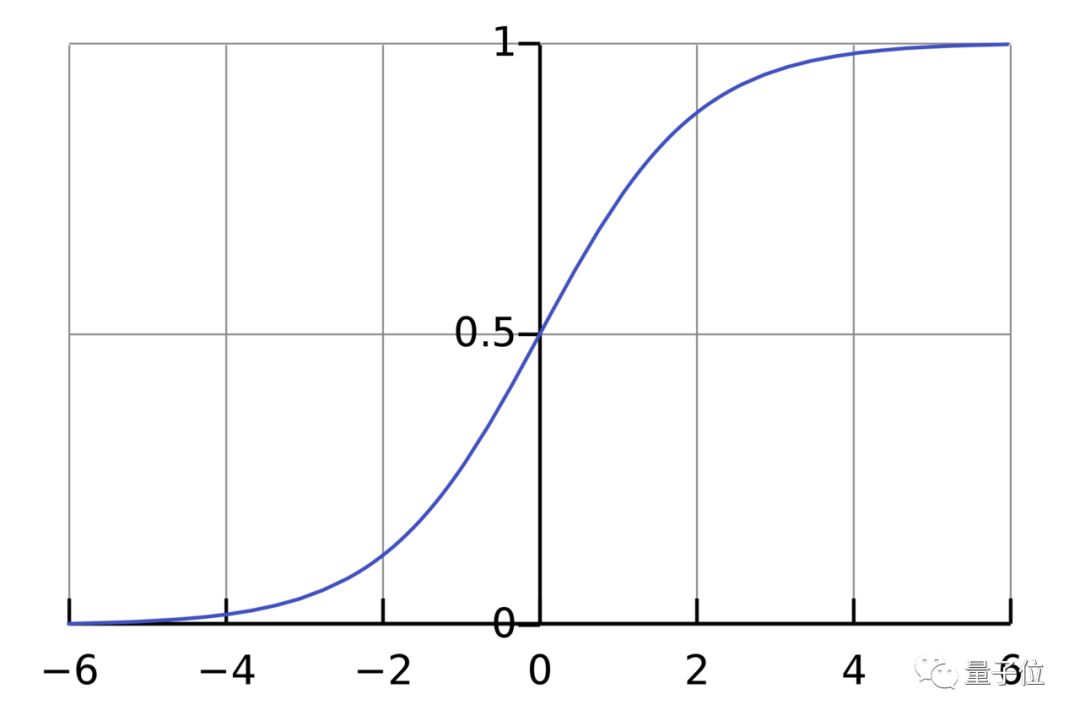

sigmoid函数的输出介于0和1，我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1，负向数值越大输出越接近0。
举个例子，上面神经元里的权重和偏置取如下数值：

是的向量形式写法。给神经元一个输入，可以用向量点积的形式把神经元的输出计算出来：

以上步骤的Python代码是：

搭建神经网络

神经网络就是把一堆神经元连接在一起，下面是一个神经网络的简单举例：

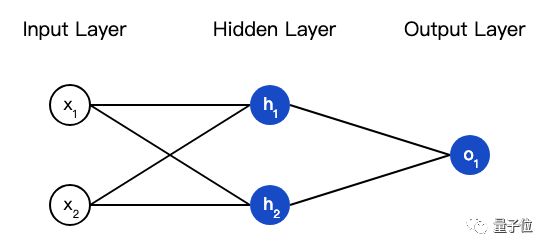
这个网络有2个输入、一个包含2个神经元的隐藏层（和）、包含1个神经元的输出层。
隐藏层是夹在输入输入层和输出层之间的部分，一个神经网络可以有多个隐藏层。
把神经元的输入向前传递获得输出的过程称为前馈（feedforward）。
我们假设上面的网络里所有神经元都具有相同的权重和偏置，激活函数都是sigmoid，那么我们会得到什么输出呢？

训练神经网络

现在我们已经学会了如何搭建神经网络，现在我们来学习如何训练它，其实这就是一个优化的过程。
假设有一个数据集，包含4个人的身高、体重和性别：

现在我们的目标是训练一个网络，根据体重和身高来推测某人的性别。

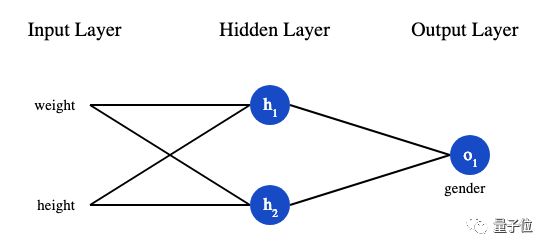
为了简便起见，我们将每个人的身高、体重减去一个固定数值，把性别男定义为1、性别女定义为0。

在训练神经网络之前，我们需要有一个标准定义它到底好不好，以便我们进行改进，这就是损失（loss）。
比如用均方误差（MSE）来定义损失：

是样本的数量，在上面的数据集中是4；
代表人的性别，男性是0，女性是1；
是变量的真实值，是变量的预测值。
顾名思义，均方误差就是所有数据方差的平均值，我们不妨就把它定义为损失函数。预测结果越好，损失就越低，训练神经网络就是将损失最小化。
如果上面网络的输出一直是0，也就是预测所有人都是男性，那么损失是：

减少神经网络损失

这个神经网络不够好，还要不断优化，尽量减少损失。我们知道，改变网络的权重和偏置可以影响预测值，但我们应该怎么做呢？
为了简单起见，我们把数据集缩减到只包含Alice一个人的数据。于是损失函数就剩下Alice一个人的方差：

预测值是由一系列网络权重和偏置计算出来的：

所以损失函数实际上是包含多个权重、偏置的多元函数：

（注意！前方高能！需要你有一些基本的多元函数微分知识，比如偏导数、链式求导法则。）
如果调整一下w1，损失函数是会变大还是变小？我们需要知道偏导数是正是负才能回答这个问题。
根据链式求导法则：

而,可以求得第一项偏导数:

接下来我们要想办法获得和的关系,我们已经知道神经元和的数学运算规则:

实际上只有神经元中包含权重,所以我们再次运用链式求导法则:


然后求

我们在上面的计算中遇到了2次激活函数sigmoid的导数,sigmoid函数的导入很容易求得:


总的链式求导公式:

这种向后计算偏导数的系统称为反向传播（backpropagation）。
上面的数学符号太多，下面我们带入实际数值来计算一下。和

神经网络的输出，没有显示出强烈的是男（1）是女（0）的证据。现在的预测效果还很不好。
我们再计算一下当前网络的偏导数：

这个结果告诉我们:如果增大,则损失函数会有一个非常小的增长.

随机梯度下降

下面将使用一种称为随机梯度下降（SGD）的优化算法，来训练网络。
经过前面的运算，我们已经有了训练神经网络所有数据。但是该如何操作？SGD定义了改变权重和偏置的方法：

是一个常数，称为学习率（learning rate），它决定了我们训练网络速率的快慢。将减去，就等到了新的权重。
当是正数时，会变小；当是负数 时，会变大。
如果我们用这种方法去逐步改变网络的权重和偏置，损失函数会缓慢地降低，从而改进我们的神经网络。
训练流程如下：

• 1、从数据集中选择一个样本；
• 2、计算损失函数对所有权重和偏置的偏导数；
• 3、使用更新公式更新每个权重和偏置；
• 4、回到第1步。

随着学习过程的进行，损失函数逐渐减小。

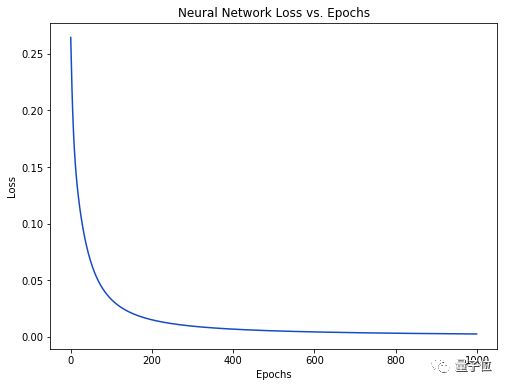
现在我们可以用它来推测出每个人的性别了

function BPNeural(MyWeightValue,MyBias,X_matrix,all_y_trues)
% all_y_trues = [1,0,0,1];
% MyBias = rand(1,3);
% MyWeightValue = rand(1,6);
% X_matrix = [-2,-1;25,6;17,4;-15,-6];
% %Input Layer
% input = MyWeightValue*X'+MyBias;
% %Hiden Layer
% Hidden = 1/(1+exp(-input));
% OutPut = 1/(1+exp(-(MyWeightValue*([Hidden,Hidden])'+MyBias)));
% disp(OutPut)
%weights
%the process of train
learn_rate = 0.1;
epochs = 1000; %number of times to loop through the entire dataset
% Fit_MyWeightValue = MyWeightValue;
% Fit_MyBias = MyBias;
data = X_matrix;
matrix_number = 1;
for epoch =1:epochs
%     disp('epoch')
%     disp(epoch)
%     disp('mod')
%     disp(mod(epoch,size(X_matrix,1)));
    if mod(epoch,size(X_matrix,1))~= 0
        choose = mod(epoch,size(X_matrix,1));
    else
        choose = mod(epoch,size(X_matrix,1))+size(X_matrix,1);
    end
    X = X_matrix(choose,:);
    y_true = all_y_trues(choose);
    sum_h1 = MyWeightValue(1)*X(1)+MyWeightValue(2)*X(1)+MyBias(1);
    h1 = sigmoid(sum_h1);%h1 is a vector
    sum_h2 = MyWeightValue(3)*X(1)+MyWeightValue(4)*X(2)+MyBias(2);
    h2 = sigmoid(sum_h2);%h2 is a vector
    sum_o1 = MyWeightValue(5)*h1 + MyWeightValue(6)*h2+MyBias(3);
    o1 = sigmoid(sum_o1);
    y_pred = o1;
    %partial L/ partial w1
    d_L_d_ypred = -2*(y_true - y_pred);
    %partial y_pred / partial w5 &w6%b3
    d_ypred_d_w5 = h1*deriv_sigmoid(sum_o1);
    d_ypred_d_w6 = h2* deriv_sigmoid(sum_o1);
    d_ypred_d_b3 = deriv_sigmoid (sum_o1);
    %partial ypred/partial h1&h2
    d_ypred_d_h1 = MyWeightValue(5)*deriv_sigmoid(sum_o1);
    d_ypred_d_h2 = MyWeightValue(6)*deriv_sigmoid(sum_o1);
    % partial h1 /partial w1&w2&b1
    d_h1_d_w1 = X(1)*deriv_sigmoid(sum_h1);
    d_h1_d_w2 = X(2)*deriv_sigmoid(sum_h1);
    d_h1_d_b1 = deriv_sigmoid(sum_h1);
    % partial h2 /partial w3&w4&b2
    d_h2_d_w3 = X(1)*deriv_sigmoid(sum_h2);
    d_h2_d_w4 = X(2)*deriv_sigmoid(sum_h2);
    d_h2_d_b2 = deriv_sigmoid(sum_h2);
    %Update weights and biases
    MyWeightValue(1) = MyWeightValue(1) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w1;
    MyWeightValue(2) = MyWeightValue(2) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w2;
    MyBias(1) = MyBias(1) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_b1;
    %h2
    MyWeightValue(3) = MyWeightValue(3) - learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w3;
    MyWeightValue(4) = MyWeightValue(4) - learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w4;
    MyBias(2) = MyBias(2) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h2_d_b2;
    %o1
    MyWeightValue(5) = MyWeightValue(5) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_ypred_d_w5;
    MyWeightValue(6) = MyWeightValue(6) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_ypred_d_w6;
    MyBias(3) = MyBias(3) - learn_rate*d_L_d_ypred*d_ypred_d_h1*d_ypred_d_b3;
   % disp(epoch)
    if mod(epoch,10) == 0
        y_preds = feedforward(MyWeightValue,MyBias,data);
        loss = mse_loss(all_y_trues,y_preds);
        Loss_matrix(matrix_number) = loss;
        epoch_matrix(matrix_number) = epoch;
        matrix_number = matrix_number+1;
%         disp('loss')
%         disp(loss)
%         disp('epoch')
%         disp(epoch)
    end
end
plot(epoch_matrix,Loss_matrix);

其中使用到的函数

function y = sigmoid(x)
y = 1/(1+exp(-x));

function y = deriv_sigmoid(x)
fx = sigmoid(x);
y = fx*(1-fx);

function y = mse_loss(y_true,y_pred)
for i=1:length(y_true)
    loss_matrix(i) = (y_true(i)-y_pred(i))^2;
end
y = mean(loss_matrix);

function y = feedforward(MyWeightValue,MyBias,X)
for i =1:size(X,1)
    h1 = sigmoid(MyWeightValue(1)*X(i,1)+ MyWeightValue(2)*X(i,2)+MyBias(1));
    h2 = sigmoid(MyWeightValue(3)*X(i,1)+ MyWeightValue(4)*X(i,2)+MyBias(2));
    o1 = sigmoid(MyWeightValue(5)*h1+ MyWeightValue(6)*h2+MyBias(3));
    y(i) = o1;
end

结果如下图所示，可以看到随着训练次数增加，损失函数不断下降。

因为所有的参数都已经达到了最优状态，所以使用这个网络模型。接下来使用这个模型进行预测。可以看到训练后的数据

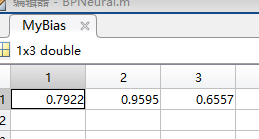
data = [-7,-3];%预测数据
feedforward(MyWeightValue,MyBias,data)

预测结果：ans =0.6783。偏向女生(1)

data = [20,2];
feedforward(MyWeightValue,MyBias,data)

ans =
0.8935。可以看到这个结果显示这次的参数明显不合适。

梯度下降算法

梯度下降的实例

一元函数的梯度下降

设一元函数为，函数的微分为。设起点为，步长为，根据梯度下降的公式，步长为。根据梯度下降的公式，经过4次迭代：

多元函数的梯度下降

设二元函数为，函数的梯度为。设起点为,步长，根据梯度下降的公式，经过多次迭代后，有

Loss function（损失函数）

损失函数也叫代价函数(cost function)，是用来衡量模型预测出来的值与真实值之间的差异函数，如果有多个样本，则可以将所有代价函数的取值求均值，记作。代价函数有下面几个性质：

• 对于每种算法来说，代价函数不是唯一的；
• 代价函数是参数的函数；
• 总的代价函数可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本；
• 是一个标量。

最常见的代价函数是均方误差函数，即

其中：

• 为训练样本的个数
• 表示估计值，表达式如下

• 是原训练样本中的值

我们需要做的是找到的值，使得最小。代价函数的图形跟我们上面画过的图很像，如下图所示。

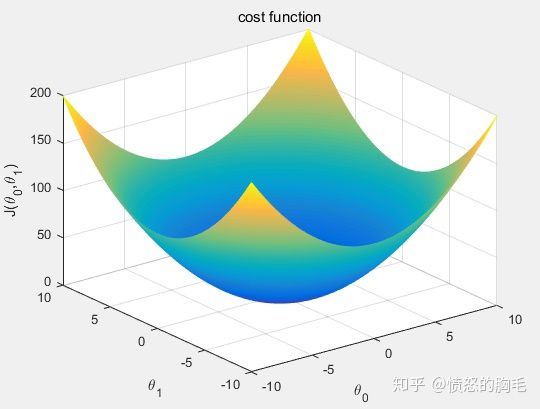
看到这个图，我们就知道可以用梯度下降算法来求可以使代价函数最小的值。
先求代价函数的梯度

这里有两个变量和，为了方便矩阵表示，我们给增加一维，这一维的值都是1，这将会乘到上。那么cost function的矩阵形式为：

这么看公式可能很多同学会不太明白，我们把每个矩阵的具体内容表示出来，大家很容易理解了。
矩阵为：

矩阵为：

矩阵为：

这样写出来后再去对应上面的公式，就容易理解了。
下面我们来举一个梯度下降算法来实现线性回归的例子。有一组数据如下图所示，我们尝试用这些点的线性回归模型。

#首先产生矩阵X和矩阵Y
# generate matrix X
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# matrix y
y = np.array([2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28]).reshape(m,1)
#按照上面的公式定义梯度函数
def gradient_function(theta, X, y):
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)
#接下来就是最重要的梯度下降算法，我们取theta_0和theta_1 的初始值都为1，再进行梯度下降过程。
def gradient_descent(X, y, alpha):
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta

通过该过程，最终求出的 线性回归的曲线如下

%matlab一元函数的梯度下降程序
clc;
close all;
clear all;
%% 
delta = 1/100000;
x = -1.1:delta:1.1;
y = x.^2;
dot = [1, 0.2, 0.04, 0.008];
figure;plot(x,y);
axis([-1.2, 1.2, -0.2, 1.3]);
grid on
hold on
plot(dot, dot.^2,'r');
for i=1:length(dot)
    text(dot(i),dot(i)^2,['\theta_{',num2str(i),'}']);
end
title('一元函数的梯度下降过程');

%matlab二元函数的梯度下降程序
pecision = 1/100;
[x,y] = meshgrid(-3.1:pecision:3.1);
z = x.^2 + y.^2;
figure;
mesh(x,y,z);
dot = [[2,3];[1.6,2.4];[1.28,1.92];[5.09e-10, 7.64e-10]];
hold on
scatter3(dot(:,1),dot(:,2),dot(:,1).^2+dot(:,2).^2,'r*');
for i=1:4
   text(dot(i,1)+0.4,dot(i,2),dot(i,1).^2+0.2+dot(i,2).^2+0.2,['\theta_{',num2str(i),'}']);
end
title('二元函数的梯度下降过程')

%matlab梯度下降的线性回归
m = 18;
X0 = ones(m,1);
X1 = (1:m)';
X = [X0, X1];
y = [2,3,3,5,8,10,10,13,15,15,16,19,19,20,22,22,25,28]';
alpha = 0.01;
theta = gradient_descent(X, y, alpha, m);
function [grad_res] =  gradient_function(theta, X, y, m)
    diff = X * theta - y;
    grad_res = X' * diff / m;
end
function [theta_res] =  gradient_descent(X, y, alpha, m)
    theta = [1;1];
    gradient = gradient_function(theta, X, y, m);
    while sum(abs(gradient)>1e-5)>=1
        theta = theta - alpha * gradient;
        gradient = gradient_function(theta, X, y, m);
    end
    theta_res = theta;
end