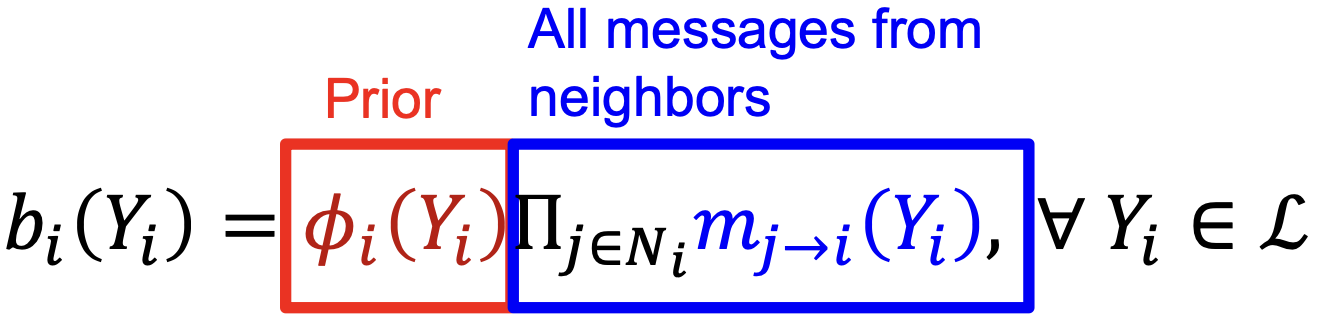Message Passing and Node Classification

主要问题：给定一个在某些节点上有标签的网络，我们如何将标签分配给网络中的所有其他节点？
例如：在网络中，一些节点是欺诈者，而另一些节点是完全受信任的。如何找到其他欺诈者和值得信赖的节点？
在Lecture3中已经讨论了将节点嵌入作为解决这个问题的方法。今天将讨论一个可替代的框架：消息传递。
直觉上，网络中存在相关性，也即相似节点是连接的。关键概念是集体分类：将标签一起分配给网络中的所有节点。我们将介绍三种技术：

• Relational classification 关系分类
• Iterative classification 迭代分类
• Belief propagation 信念传播

个人行为在网络中是相互关联的，相关性体现在附近的节点具有相同的颜色（属于同一类）。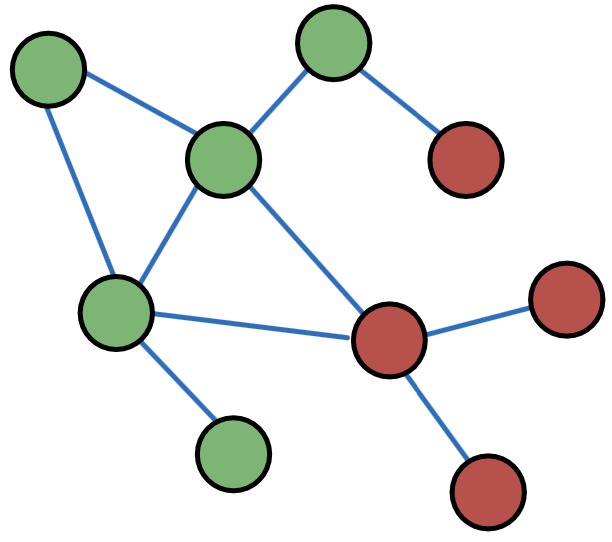

导致相关性的主要依赖类型：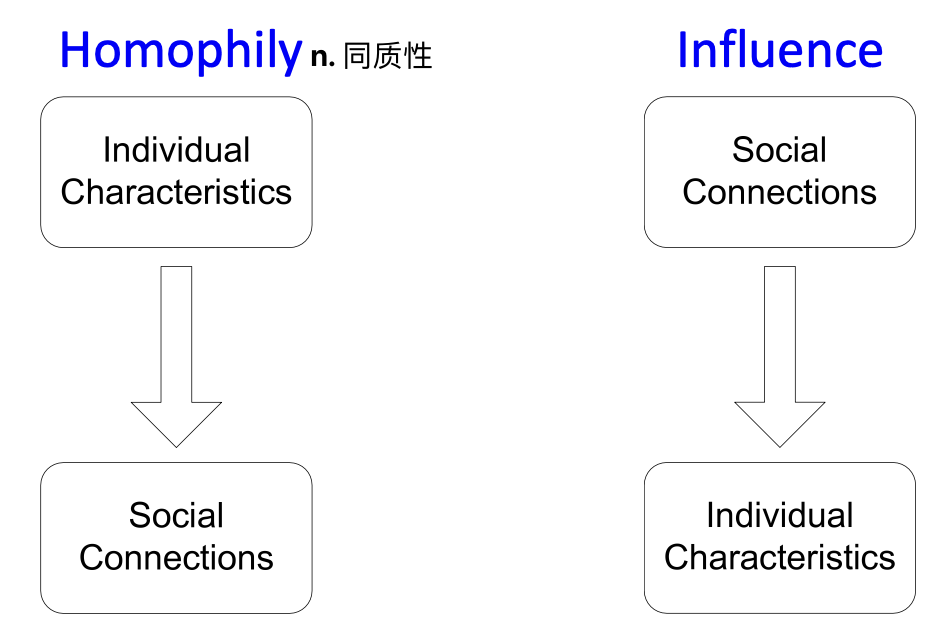

同质性Homophily：个体与相似人交往和结合的倾向。“物以类聚”，根据各种属性（如年龄、性别、组织角色等），在大量网络研究中都观察到了这一点。例如，专注于同一研究领域的研究人员更有可能建立联系（在会议上开会、在学术讲座中互动等）。
同质性例子：在线社交网络，节点=人，边=关系，节点颜色=兴趣（如运动、艺术等），兴趣相同的人由于同质性而联系更紧密。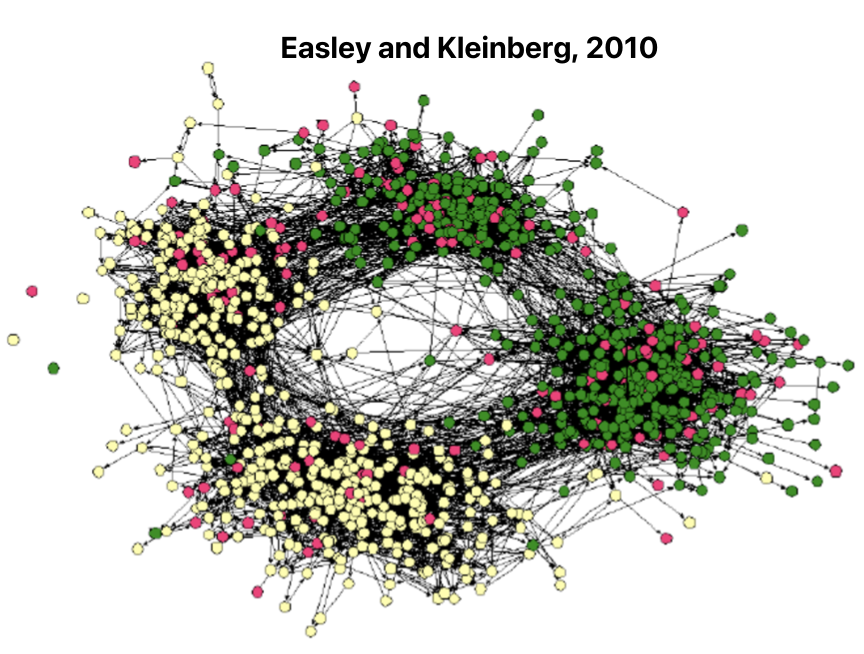

影响Influence：社会关系可以影响一个人的个性特征。如，我向我的朋友推荐我的音乐偏好，直到他们中的一个渐渐喜欢上我最喜欢的类型。
我们如何利用网络中观察到的这种相关性来帮助预测节点标签？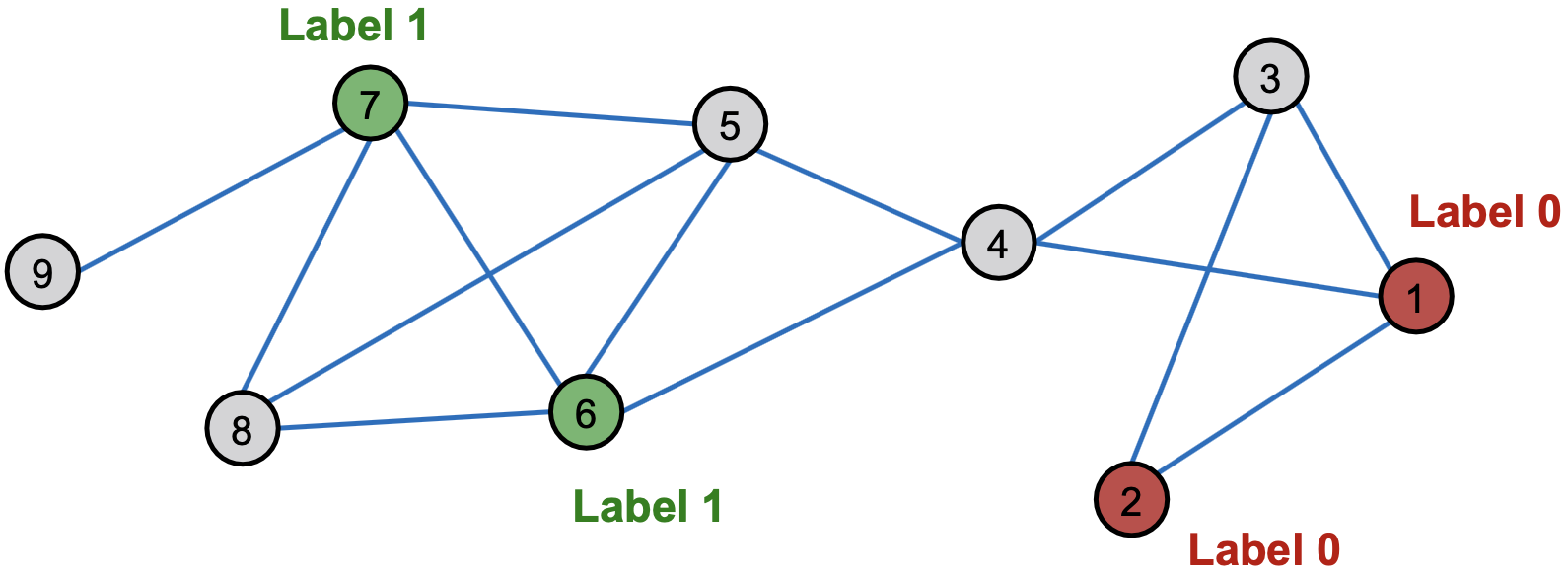
我们如何预测灰色节点的标签？
Motivation1，相似节点在网络中通常相近或直接连接：

• Guilt-by-association：如果我连接到带有标签的节点, 那么我很可能会有标签
• 例子：恶意/良性网页，恶意网页相互链接，以提高可见性，看起来可信，并在搜索引擎中排名更高

Motivation2，网络中节点的标签分类依赖于：

• 的特征；
• 的邻居节点的标签；

• 的邻居节点的特征。

  半监督学习

  给定图，一些带有标签的节点，找到余下节点的类别。主要假设是网络中存在同质性。
  
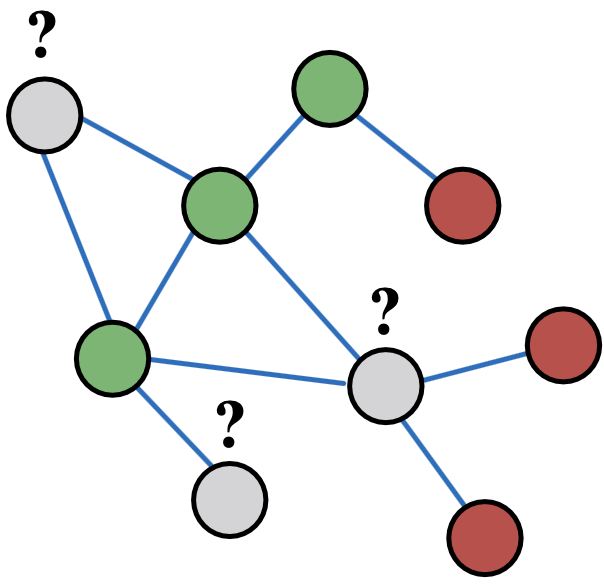
  例子：
  设为个节点的邻接矩阵，为标签向量，表示属于类1，表示属于类0。目标：对余下的没有标签的节点分类。

  Collective Classification方法

  应用：

• 文件分类

• 词性标注
• 链路预测
• 光学字符识别
• 图像/三维数据分割
• 传感器网络中的实体解析
• 垃圾邮件和欺诈检测

直觉上，使用相关性对互连节点进行同时分类。使用概率框架，Markov假设一个节点的标签依赖于其邻居的标签。Collective classification包括3个步骤：

• step1: 局部分类，分配初始标签。基于节点特征预测标签，属于标准的分类任务，没有使用网络信息。
• step2: 关系分类，捕获节点之间的相关关系。基于节点标签或节点邻居的特征来学习一个分类器进行分类，用到了网络信息。
• step3: 集体推断，通过网络传播关系。对每个节点迭代地运用关系分类，迭代至邻居标签间的不一致性最小化，网络结构影响最终的预测。

对没有标签的节点如何预测其标签？每个节点有个特征向量，部分节点的标签给定，基于所给的网络和特征，找到。
我们聚焦于半监督节点分类，直观上基于同质性，相似节点一般相近或直接相连。这里介绍三种技术：

• Relational classification 关系分类
• Iterative classification 迭代分类
• Belief propagation 信念传播

  Relational Classification and Iterative Classification

  Relational Classification

  基本思想：节点的类概率是其邻居类概率的加权平均值。对于有标签的节点，用真实标签来表示初始标签；对于无标签的节点，初始化。以随机顺序来更新所有节点，直至聚合或达到最大迭代次数。
  对每个节点和标签更新：
  若边有权重信息，则可以为和的边权重。表示节点有标签的概率。
  挑战：

1. 聚合没有保障；
2. 模型没有使用节点的特征信息。

   例子

   初始化

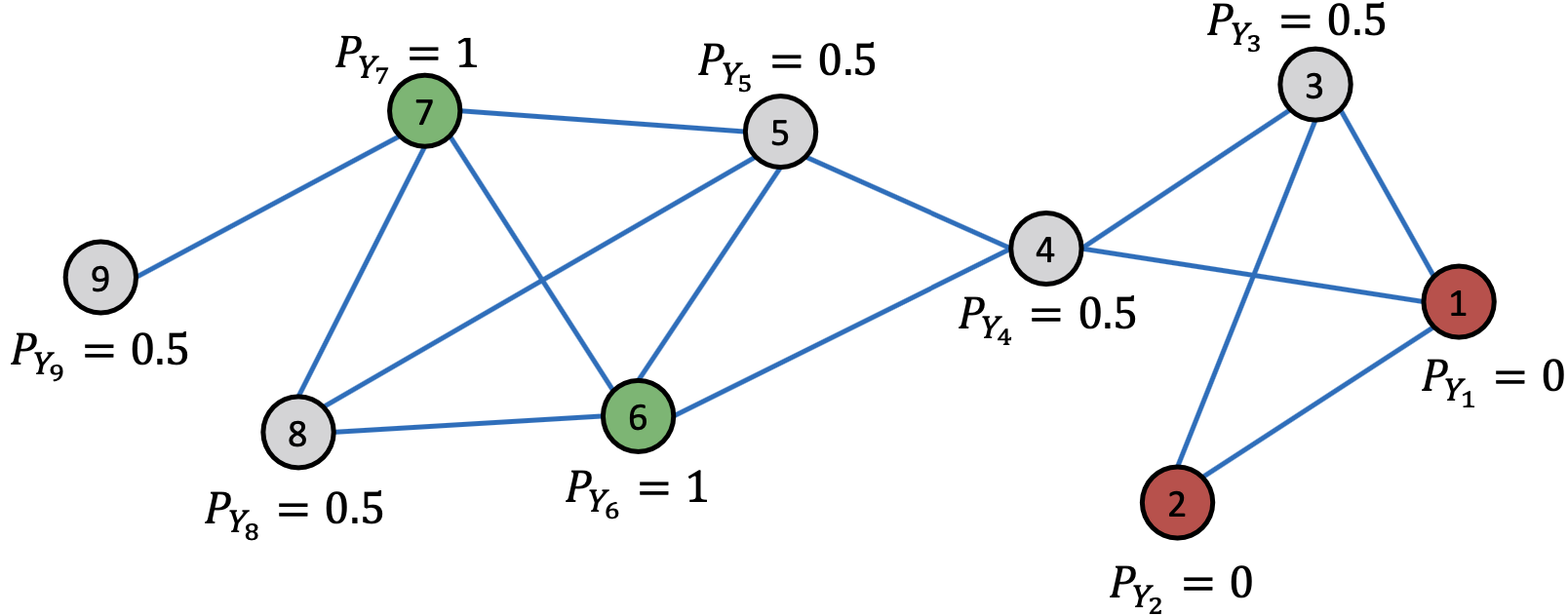
• 所有有标签的节点，用其标签；
• 没有标签的节点，标签设为0.5（属于class 1的概率为0.5）

设

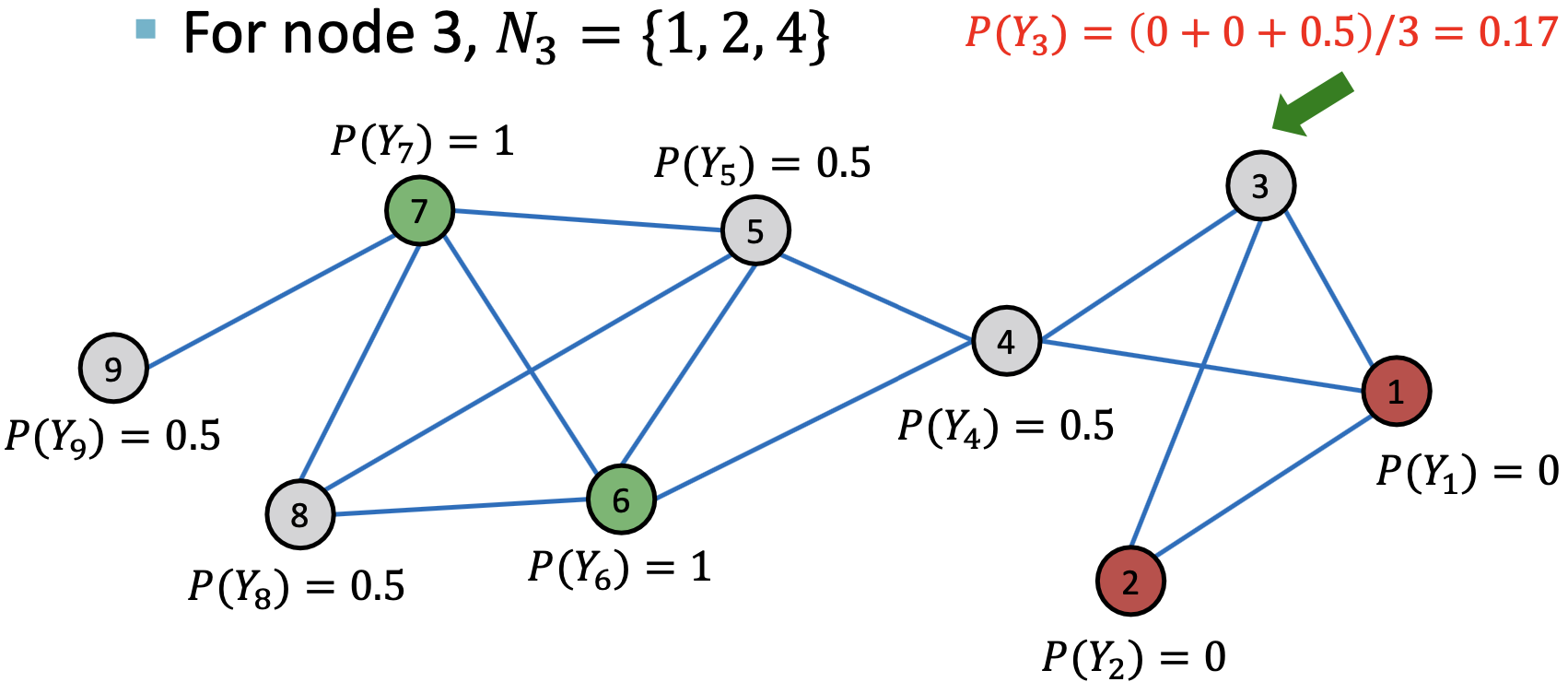
1st Iteration, Update Node 3

1st Iteration, Update Node 4

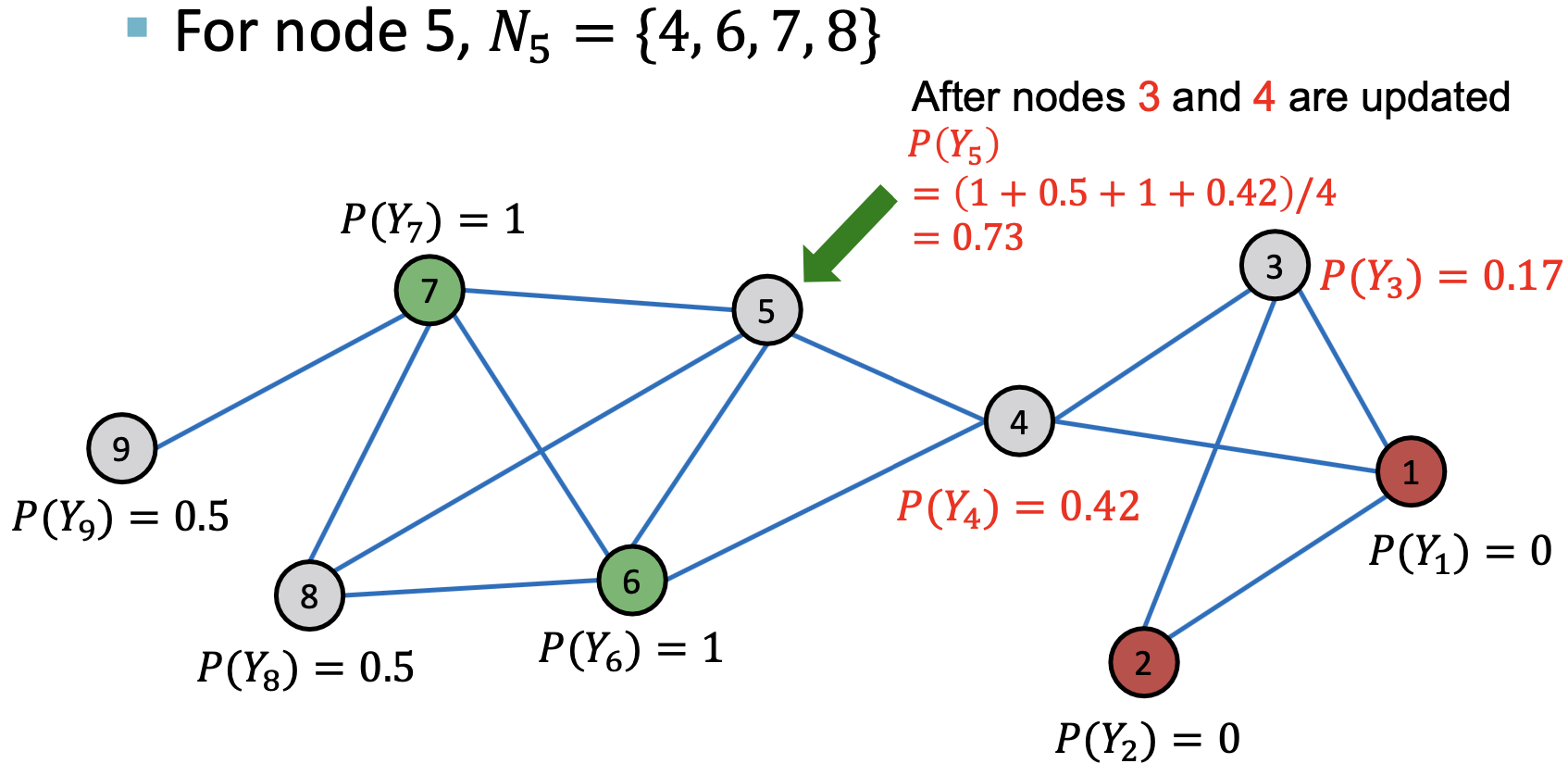
1st Iteration, Update Node 5

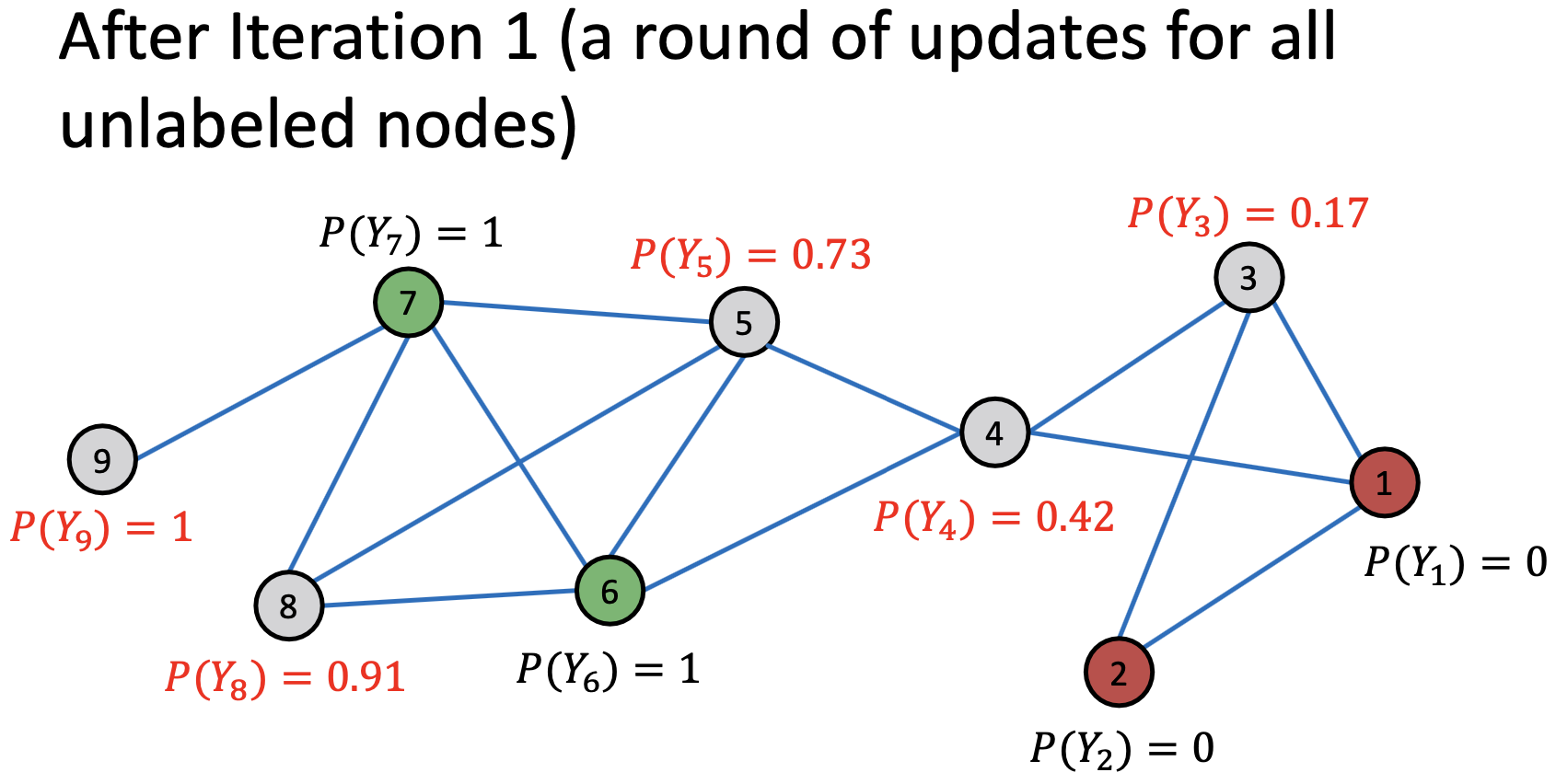
After 1st Iteration

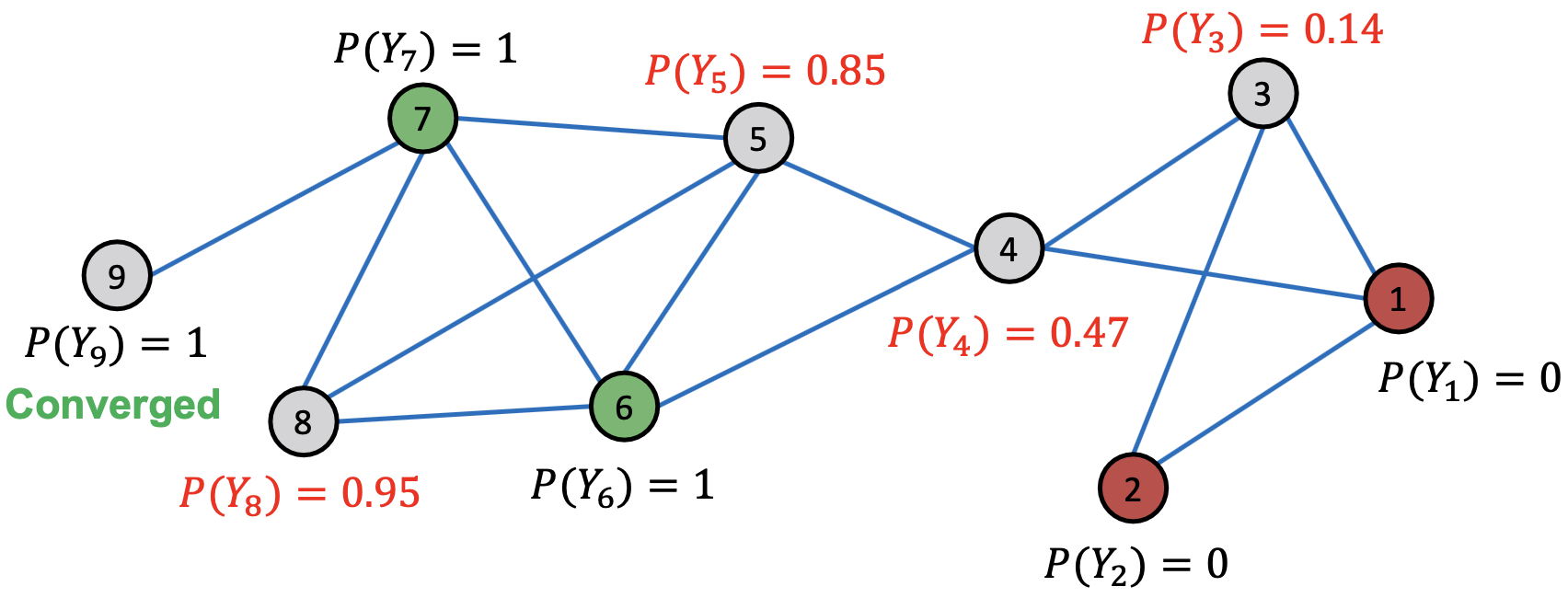
After 2st Iteration

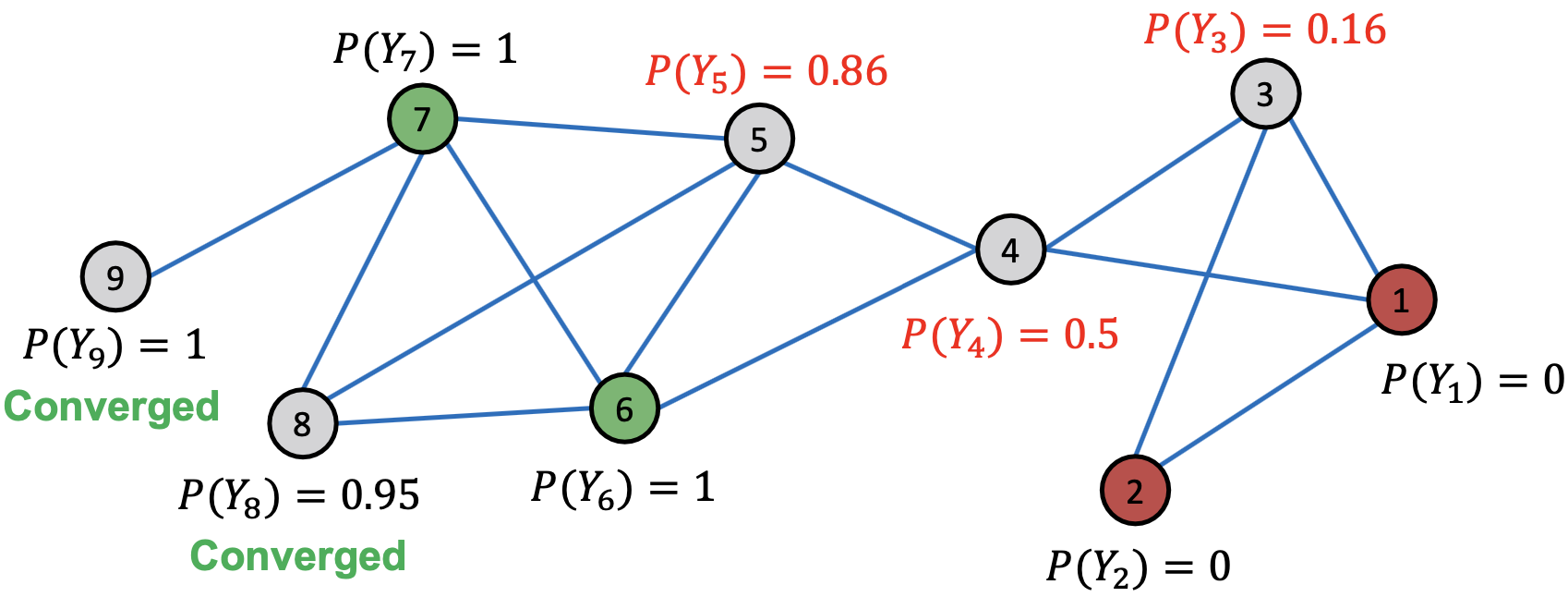
After 3st Iteration

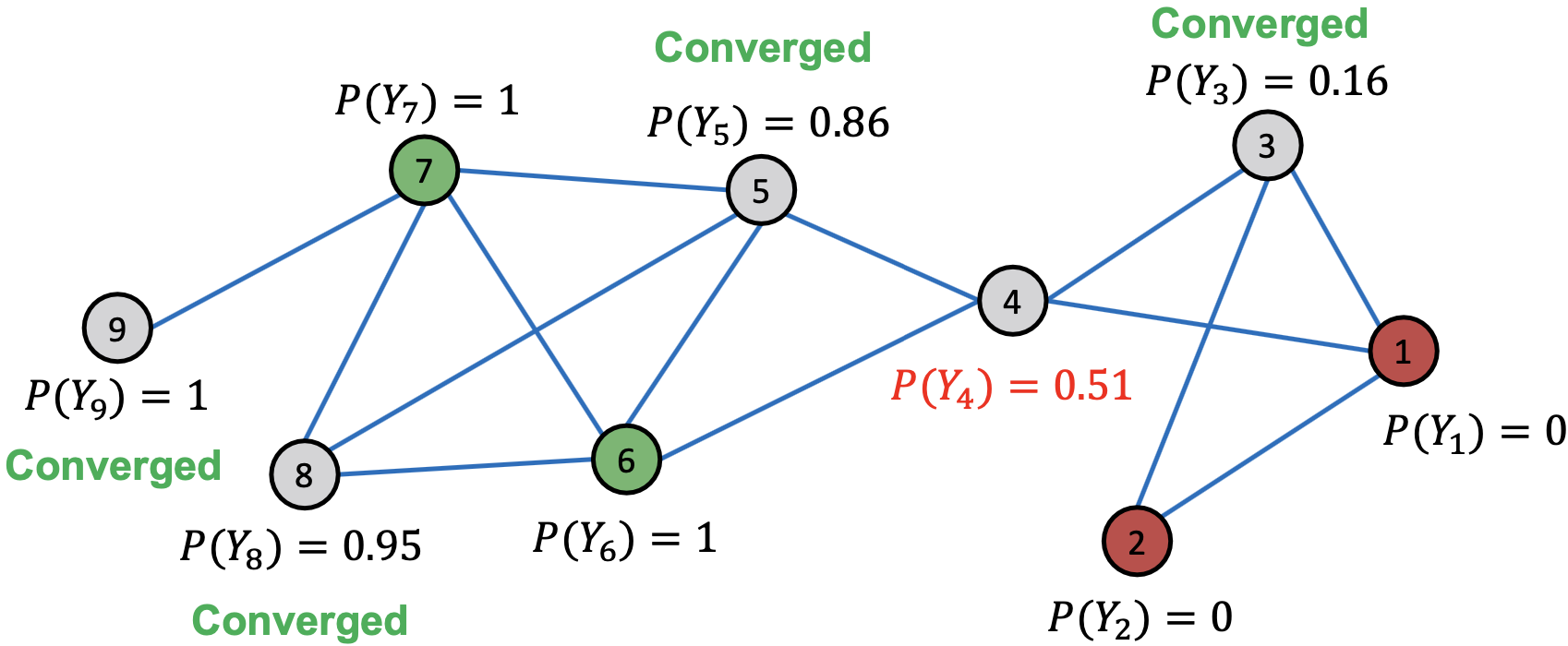
After 4st Iteration

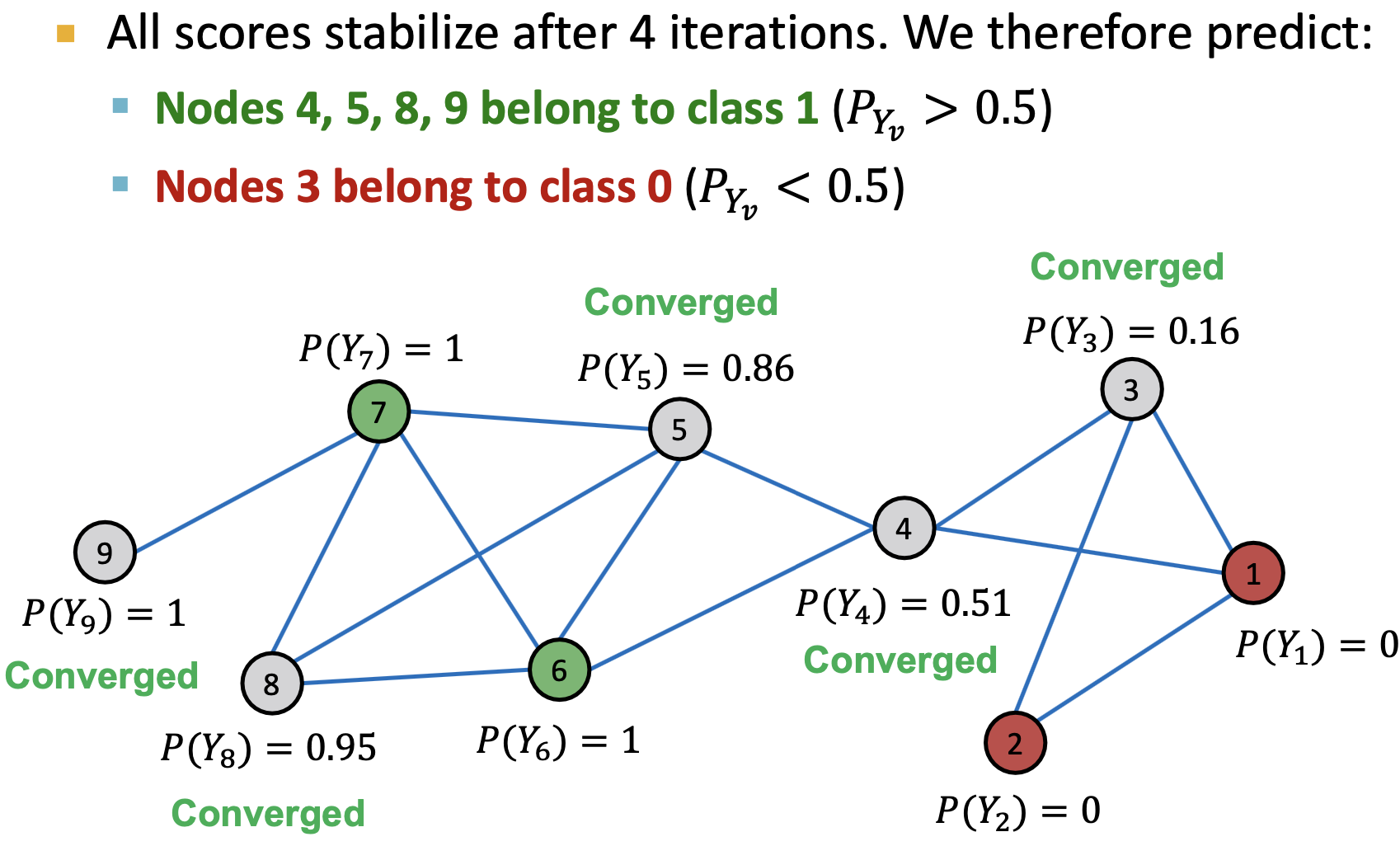
Convergence

Iterative Classification

关系分类器不使用节点属性，那要如何利用它们呢？
迭代分类的主要思想是基于节点的属性和其邻居集合的标签，来对节点分类。
输入：图。表示节点的特征向量，部分节点有标签为。
任务：预测无标签节点的标签。
方法：训练两个分类器，=基于节点特征向量来预测节点标签，=基于节点特征向量和总结的邻居的标签来预测节点标签。
我们要如何summary节点的邻居的标签？

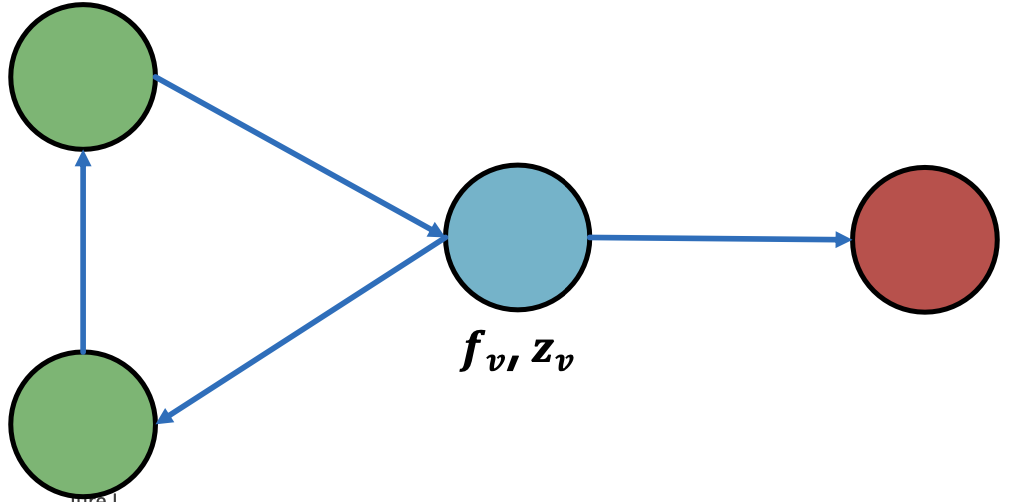
迭代分类的框架：
Phase1: 基于节点属性单独分类

• 在训练集上，训练分类器（如线性分类、神经网络等）
• 用来基于预测
• 用来基于和summary 的邻居的标签预测

Phase2: 迭代至聚合

• 在测试集上，基于分类器设置标签，计算和用预测标签
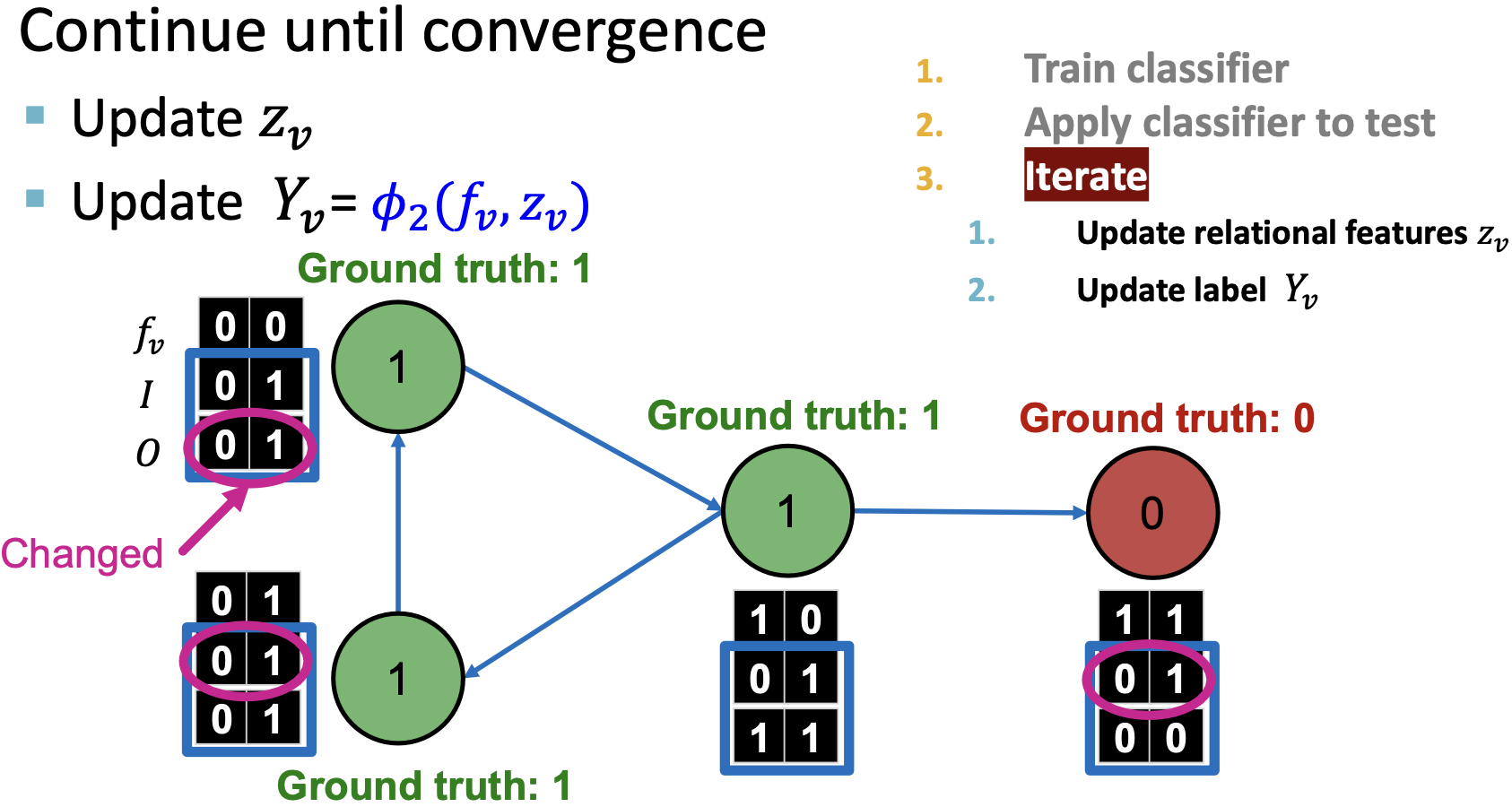
• 重复每个节点，（1）对所有，基于更新；（2）基于新的更新
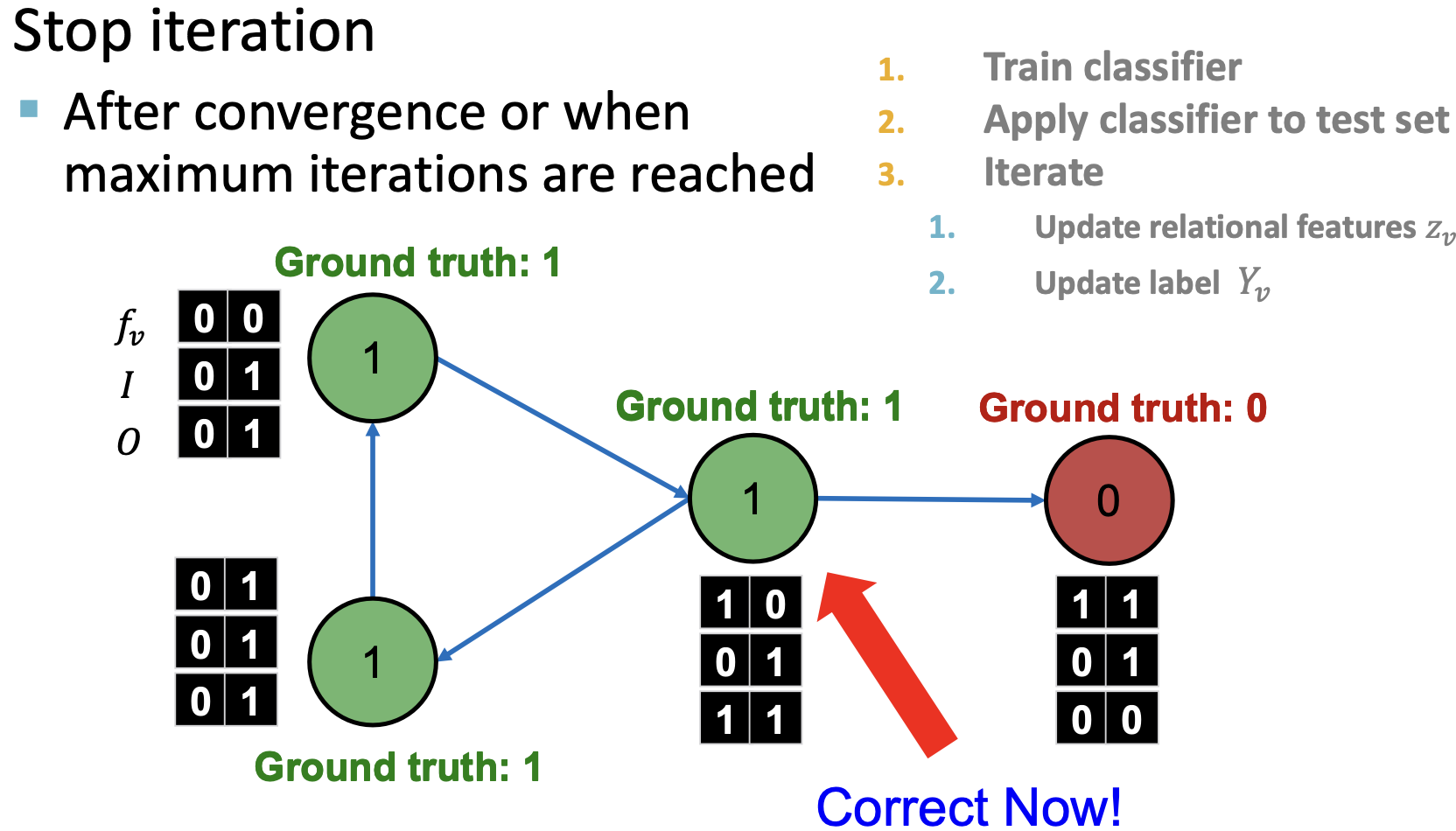
• 迭代，直到类标签稳定或达到最大迭代次数

注：不保证收敛。

例子：网页分类

输入：网页的图。
节点：网页。
边：网页间的超链接。有向边：从一个网页指向另一网页。
节点特征：网页描述。为了简单起见，我们只考虑2 binary 特征。
任务：预测网页的主题。
Baseline：基于binary 节点属性，训练一个分类器（如线性分类）来对网页分类。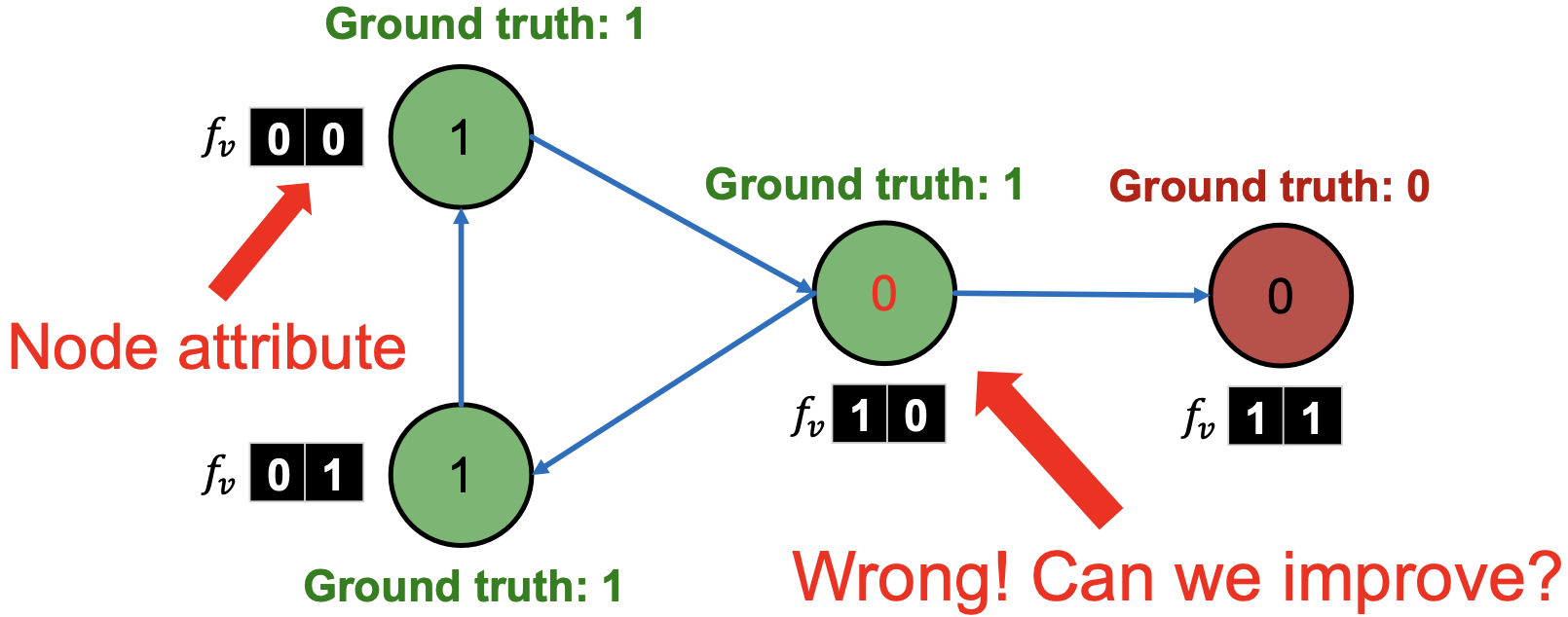

每个节点维护邻居标签的向量，表示进入的邻居标签信息向量，表示出去的邻居标签信息向量。
如果至少有一个传入页面标记为0，类似定义。

在不同训练集上，训练两个分类器：

• 绿圈，仅有节点属性：
• 红圈，节点属性和链接向量：

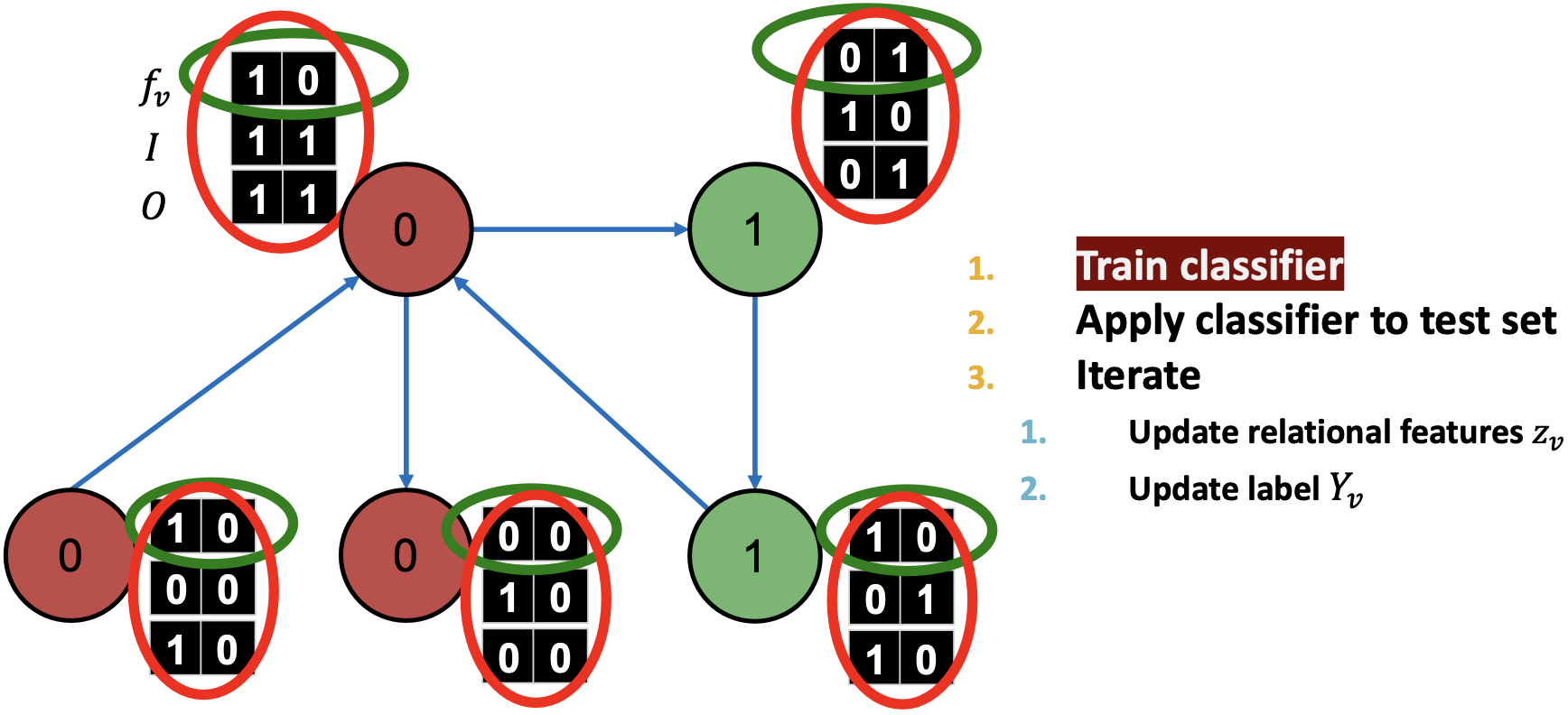
在测试集上，使用训练的节点特征向量分类器来设置：


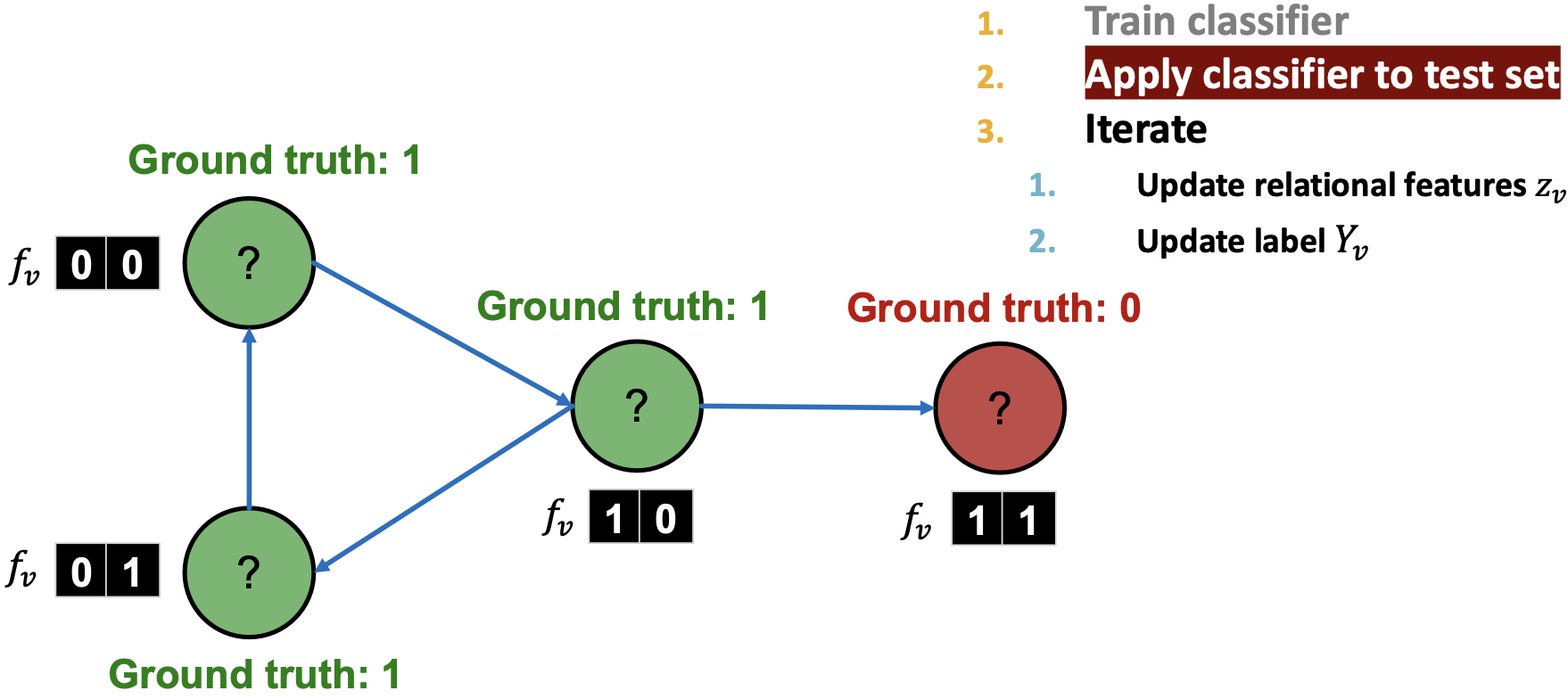
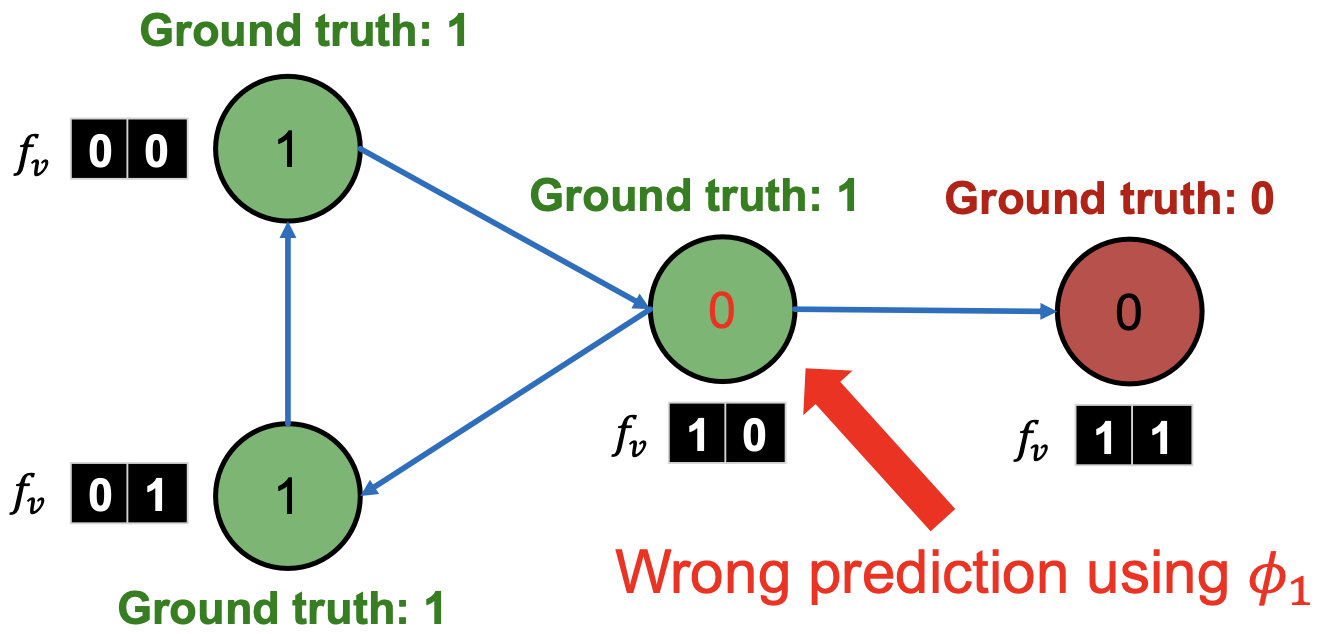
对所有节点更新：

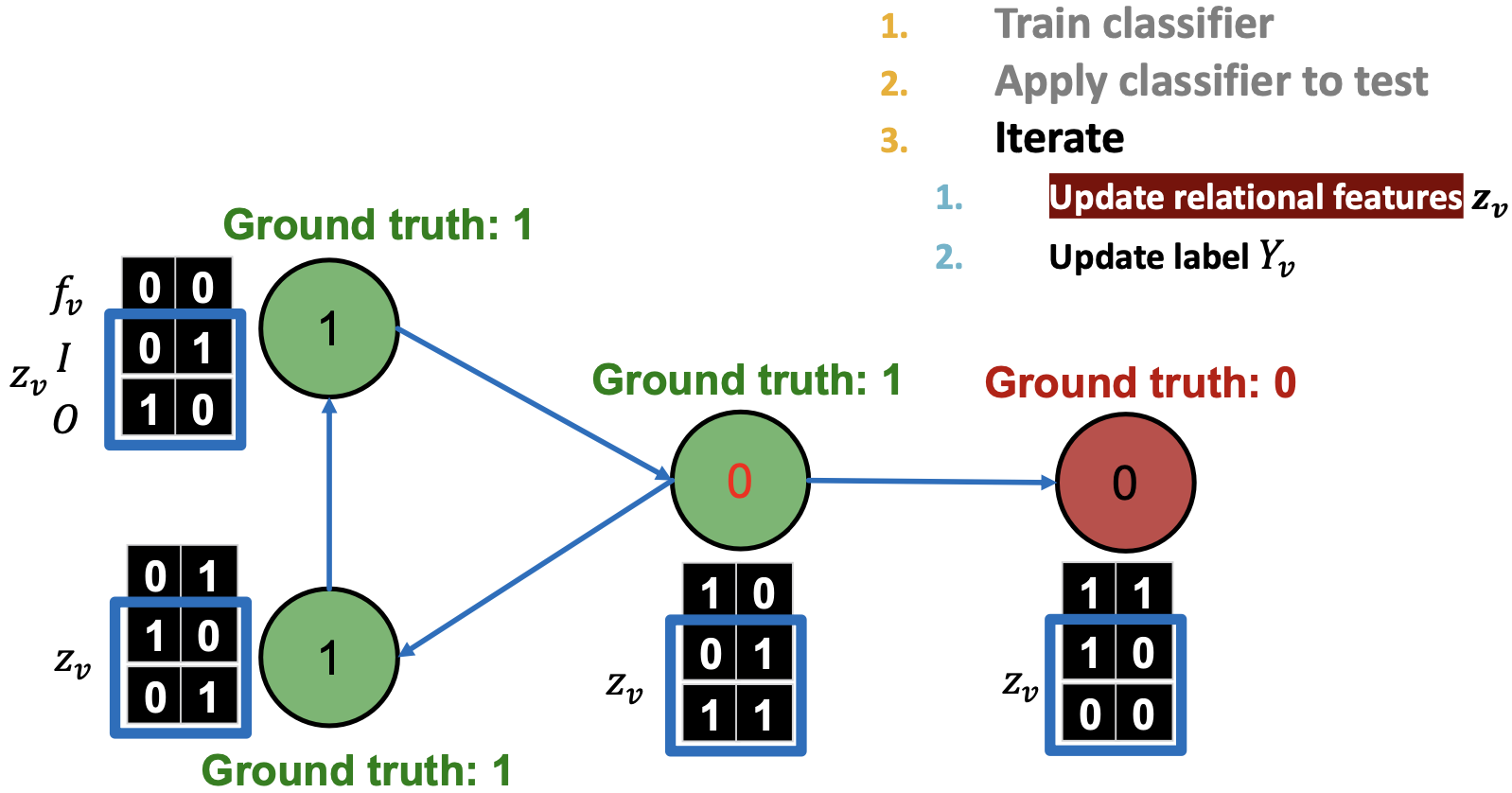
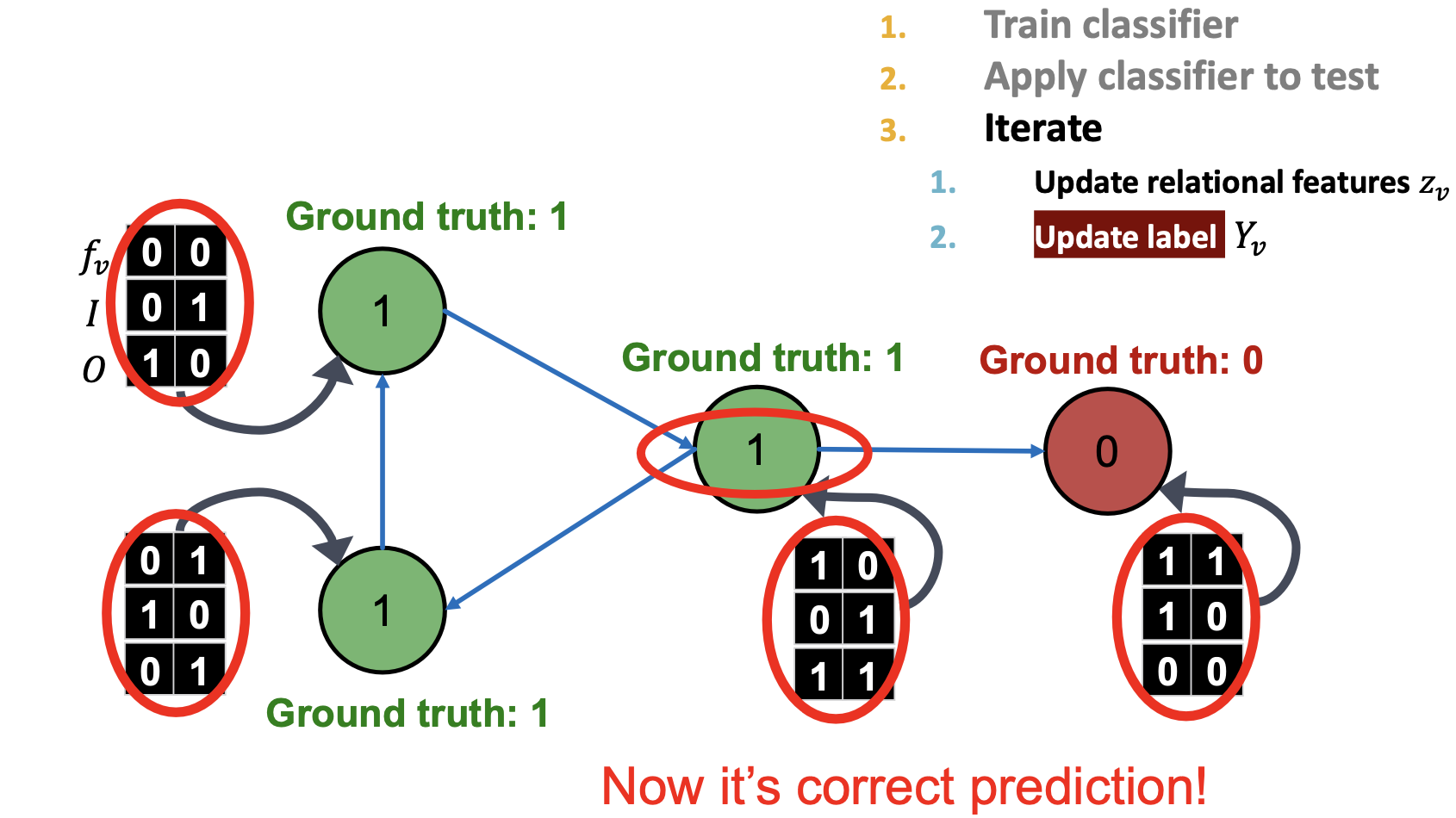
对所有节点重新用分类：

Summary

Relational classification

• 基于节点邻居，迭代更新节点属于某一类标签的概率

Iterative classification

• 改进集合分类以处理属性/特征信息

• 基于特征信息和邻居的标签来对节点分类

  Belief Propagation

  信念传播是一种动态规划方法，用于回答图的概率查询（例如节点属于第1类的概率）。相邻节点相互“交谈”，传递消息的迭代过程。
  
  达成共识后，计算最终信念。
  任务：计算图中节点的数量。
  条件：每个节点只能与其邻居交互（传递消息）。
  算法：

• 定义节点顺序（形成路径）

• 边方向根据节点顺序确定，边方向定义节点的消息传递顺序
• 对于节点，从1到6：计算从节点到的消息（到目前为止统计的节点数）；从节点到传递消息。

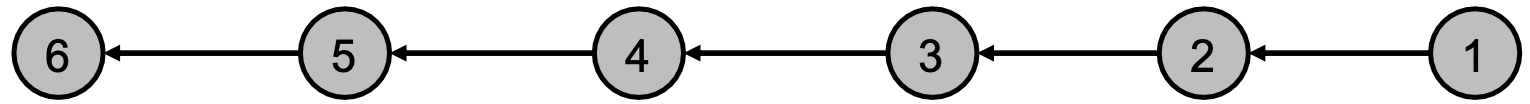
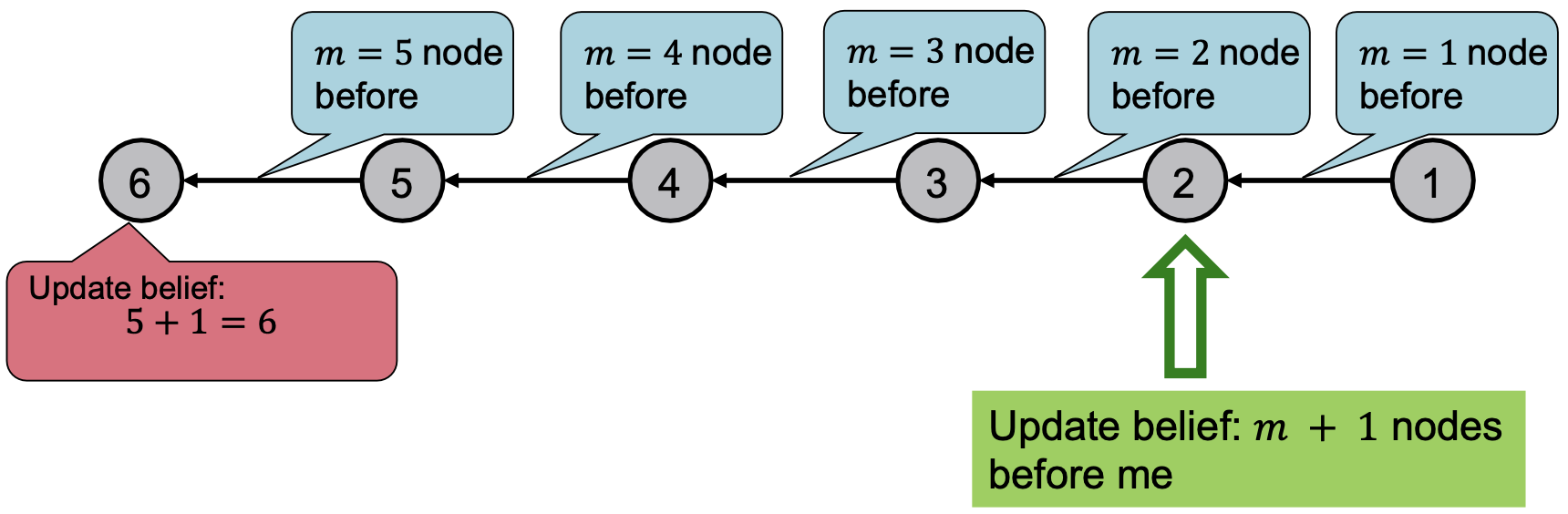
解决方法：每个节点都会侦听来自其邻居的消息，对其进行更新，并将其传递。表示消息。

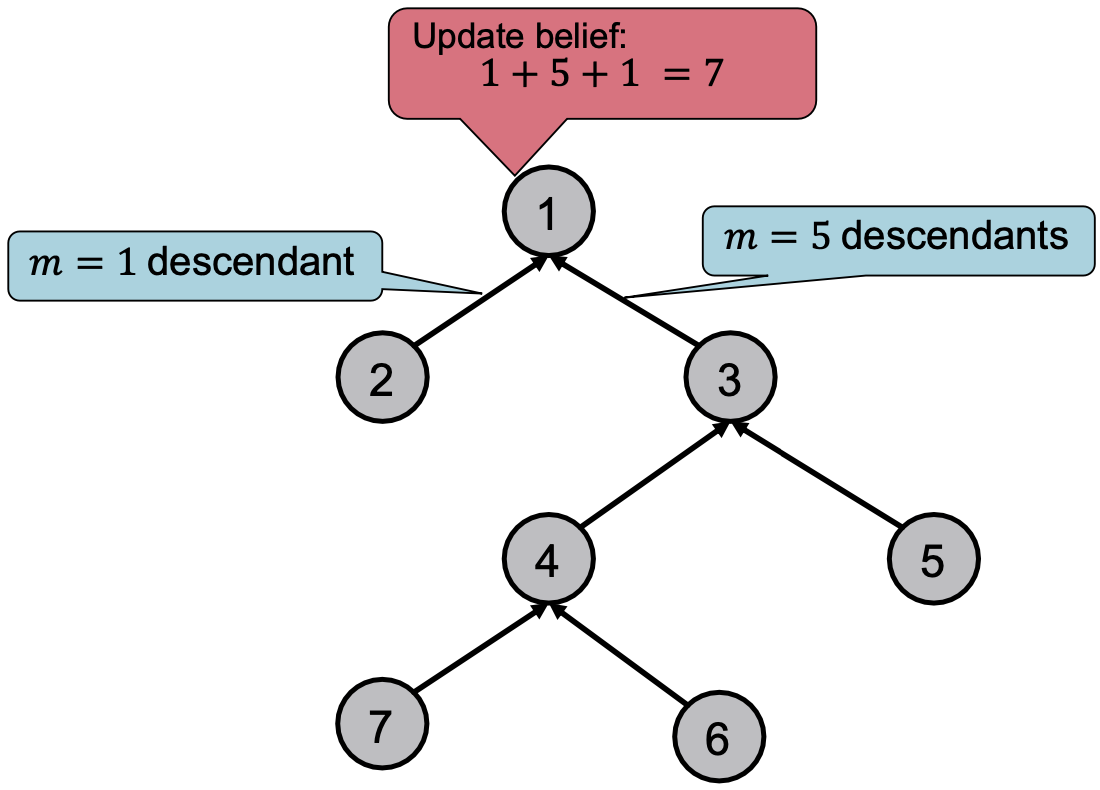
我们不仅可以在路径图上执行消息传递，还可以在树结构图上执行消息传递。定义从叶节点到根节点的消息传递顺序：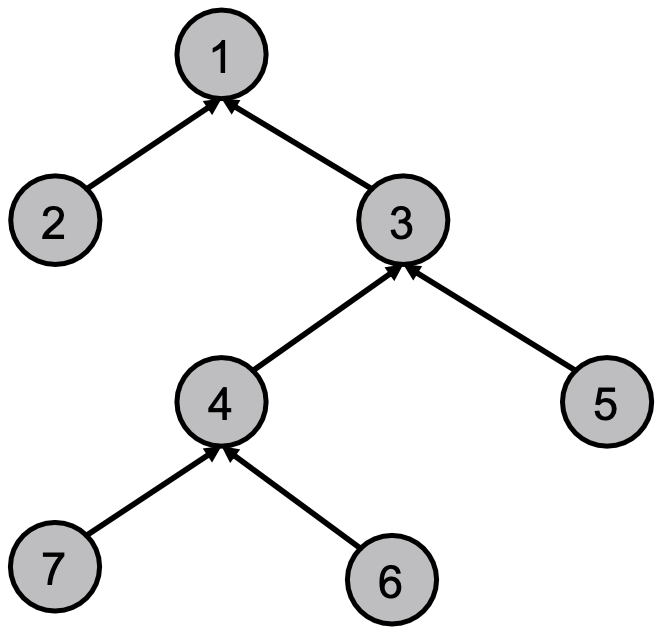

在树结构中更新信念：（descendant 后代，子孙，后裔）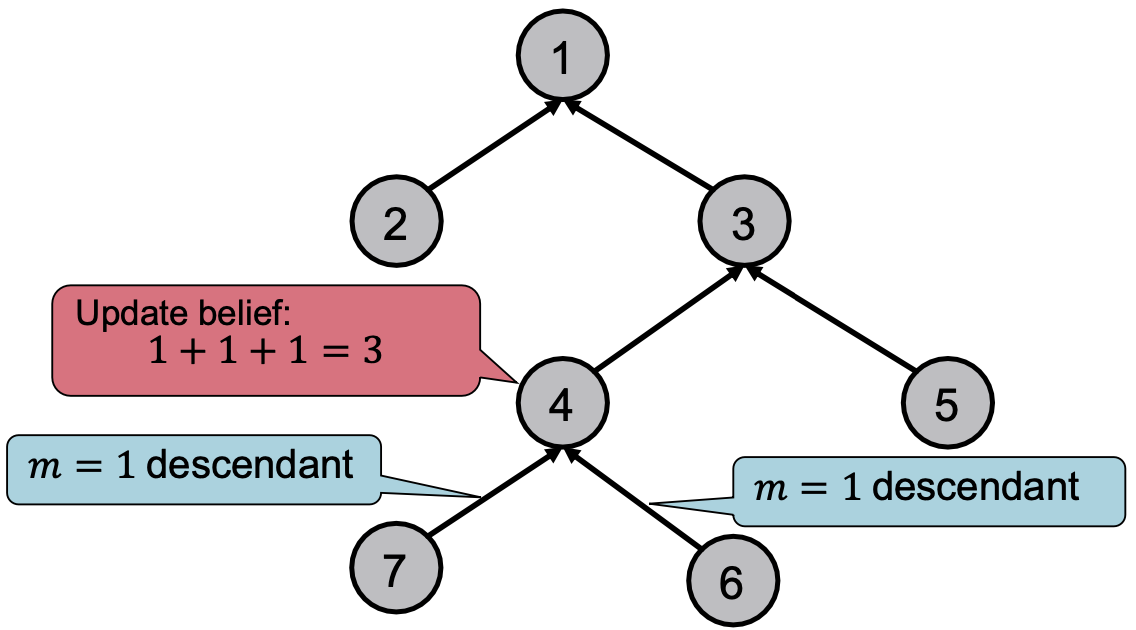

Loopy BP Algorithm

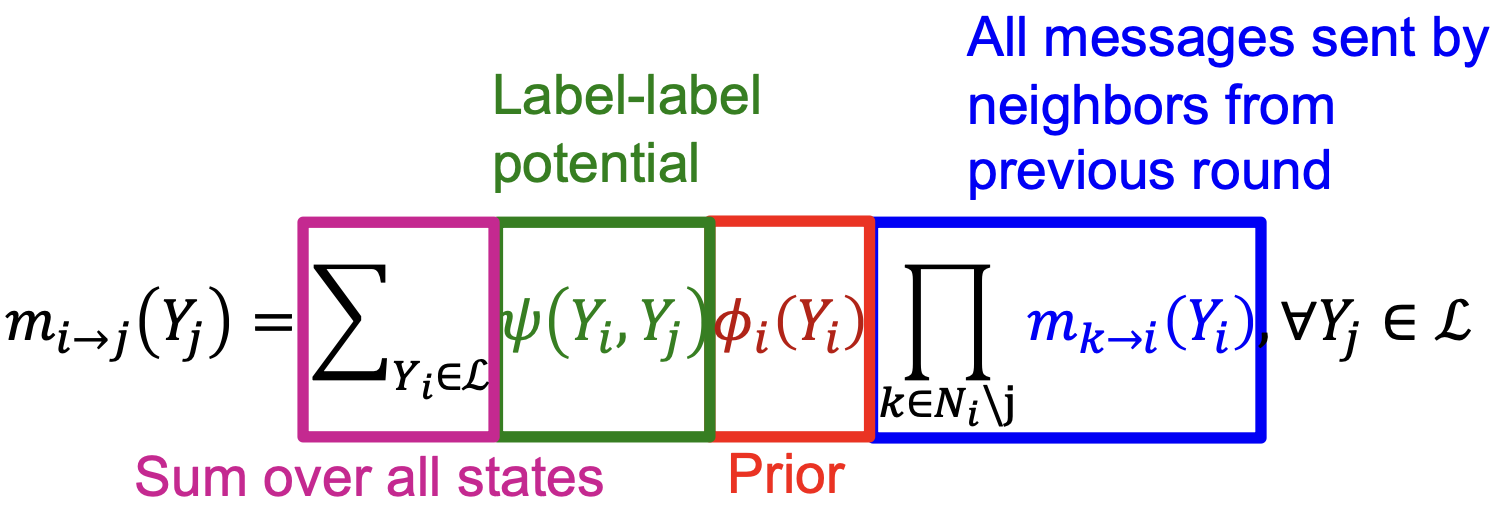
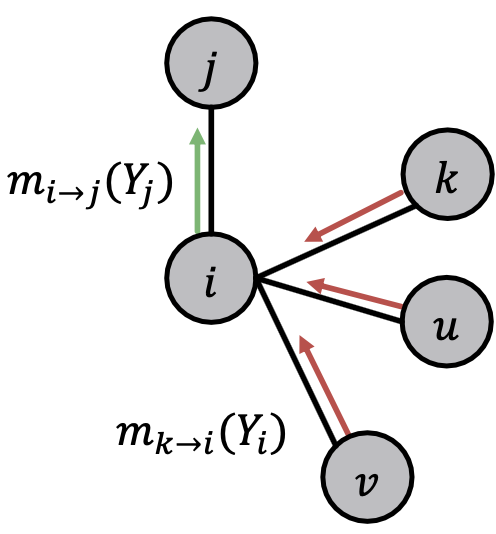
什么样的信息会从传递到？

• 取决于从邻居那获取到的是什么
• 每一位邻居都会给传递一条它对所处状态信仰的信息

符号：

• Label-label potential matrix ：节点与其邻居之间的依赖关系。是基于邻居属于类时，节点属于类的概率比例。
• Prior belief ：是节点属于类的概率比例。
• 是的信息，用来估计属于。
• 是所有类/标签的集合。

1. 初始化所有信息为1
2. 对每个节点重复：

汇聚后：=节点 belief 为类

例子

现在我们考虑一个带循环的图，不再有节点排序。我们采用与前面相同的算法：从任意节点开始，沿着边更新邻居节点。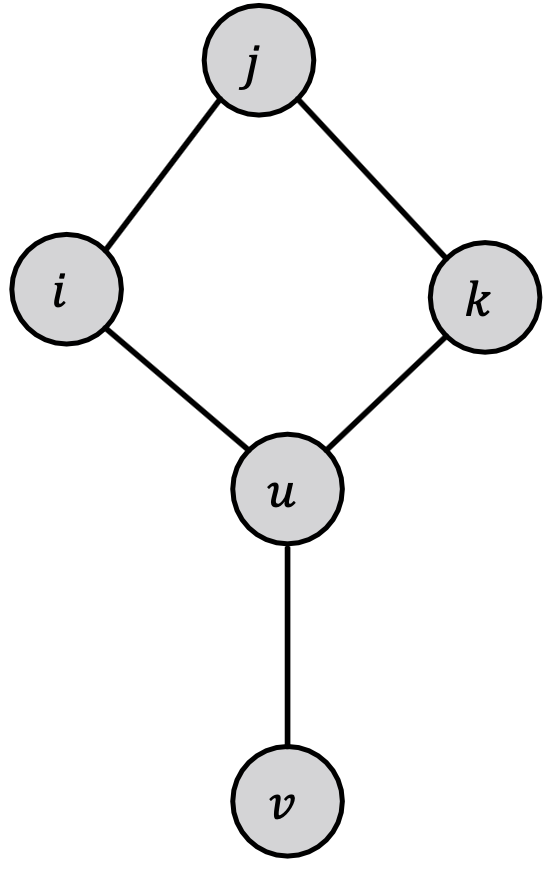

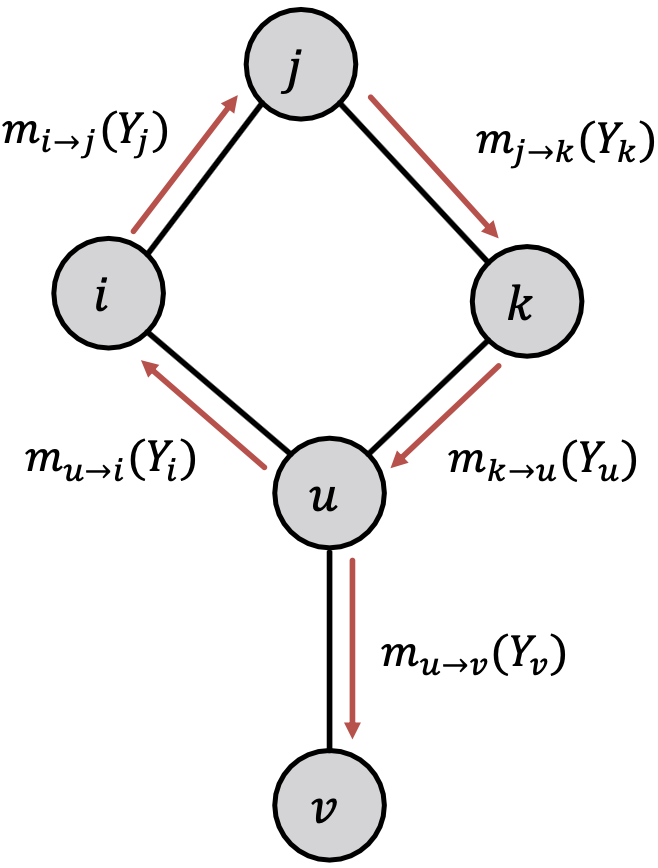
来自不同子图的消息不在独立，但我们仍然可以运行BP，只是它会在循环中传递消息。

• 信念可能不会聚合。信息是基于的初始belief，不是的单独证据。的初始belief（可能不是正确的）被循环强化，。
• 然而，在实践中，对于包含许多分支的复杂图，循环BP仍然是一种很好的启发式方法。

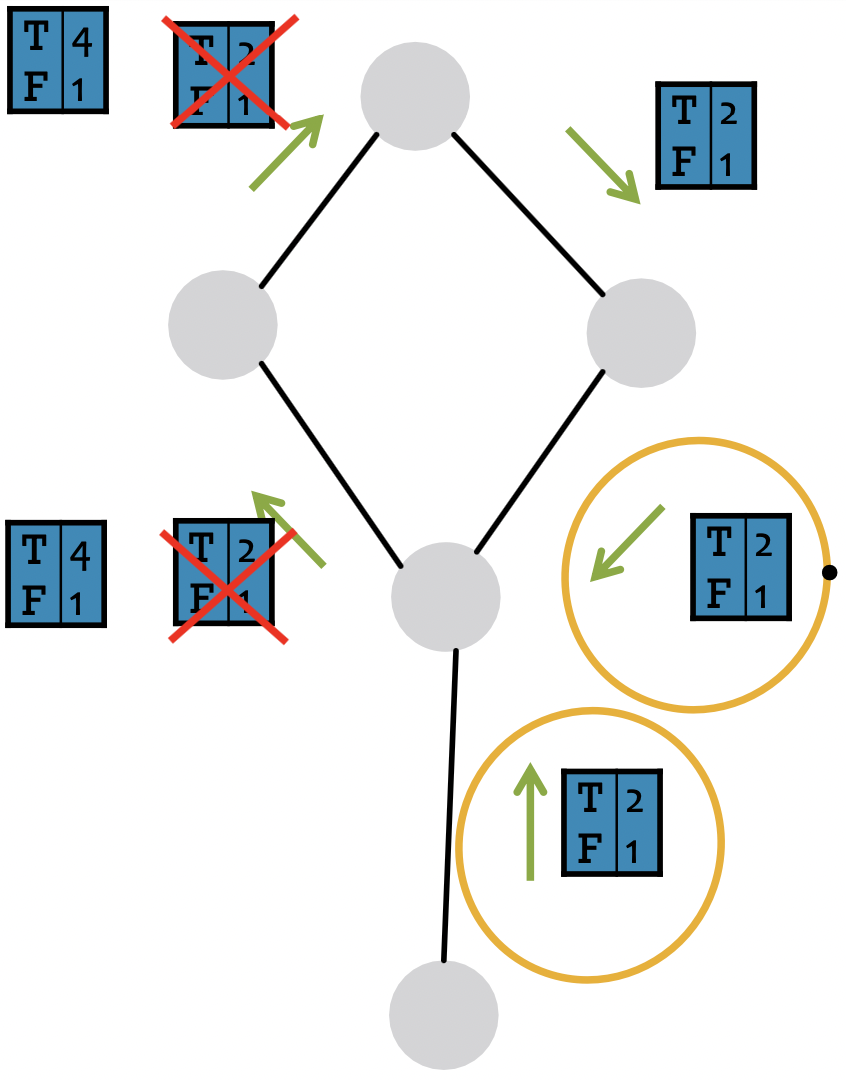
• 消息不断循环：2, 4, 8, 16, 32, … 越来越多的节点相信这些变量是T！
• BP错误地将此消息视为变量为T（true）的单独证据。
• 将这两条消息相乘，就好像它们是独立的一样。但它们实际上并不来自图的独立部分，通过循环一方影响另一方。

这是一个极端的例子。在实践中，循环影响往往很弱。（由于周期较长或至少包含一个弱相关性。）

Advantages of Belief Propagation

优点：

• 易于并行化和编程
• 概述：适用于具有任何形式potentials的任何图模型，potential可以是高阶的，如

挑战：

• 停止时不保证收敛，尤其是当有许多闭合回路时

potential函数（参数）：

• 需要训练来估计

  Summary

  我们学习了如何利用图中的相关性对节点进行预测。
  关键技术：

• 关系分类

• 迭代分类
• 循环信念传播