How Expressive are Graph Neural Networks?
key idea:基于局部网络邻域生成节点嵌入。
节点使用神经网络从它们的邻居聚合信息。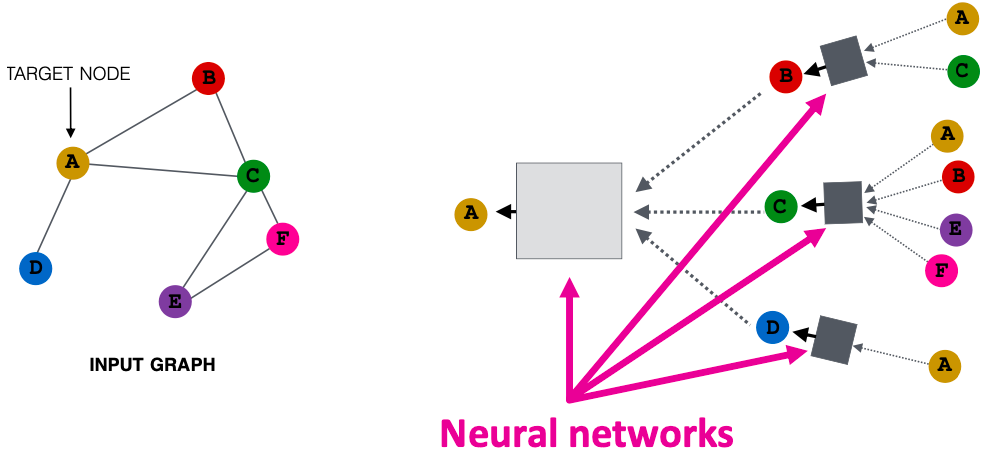
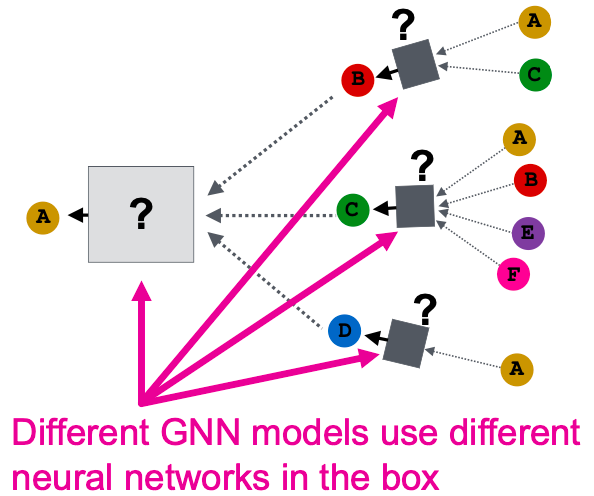
GNN有多强大?
- 已有许多GNN模型被提出(如GCN、GAT、GraphSAGE、design space)。
- 这些GNN模型的表达能力(区分不同图结构的能力)是什么?
- 如何设计一个最具表现力的GNN模型?
GNN Model Example1
GCN (mean-pool) [Kipf and Welling ICLR 2017]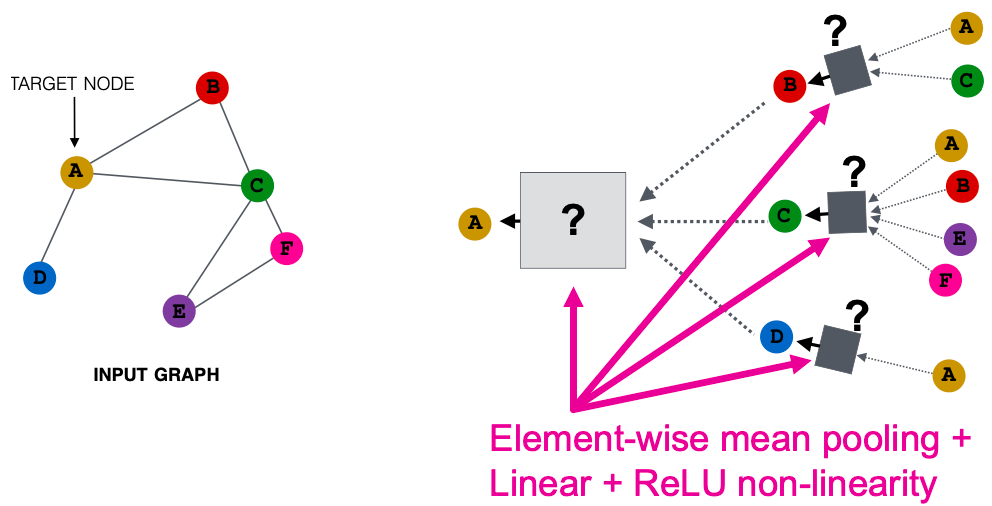
GraphSAGE (max-pool) [Hamilton et al. NeurIPS 2017]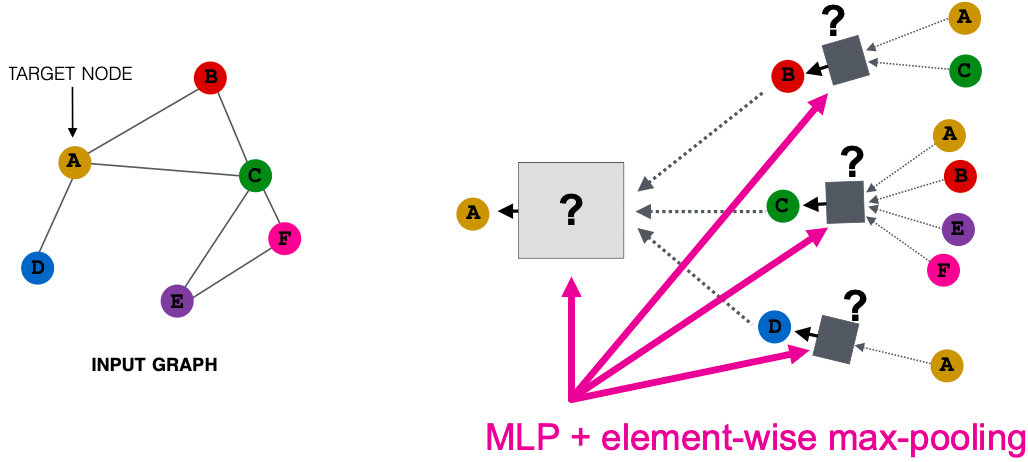
节点颜色
我们使用节点相同/不同颜色来表示具有相同/不同特征的节点。如,下图假设所有节点共享相同的特征。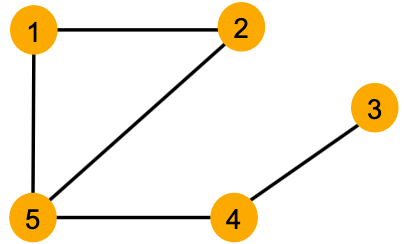
关键问题:GNN能在多大程度上区分不同的图结构?
局部邻居结构
我们特别考虑图中每个节点周围的局部邻域结构。如,
- 节点1和5有不同的邻域结构,因为它们有不同的节点度。
- 节点1和4都有相同的度2,但它们有不同的邻域结构,因为它们的邻居有不同的节点度。(节点1的邻居的度为2和3,节点4的邻居的度为1和3)
- 节点1和2有相同的邻居结构,因为它们在图中是对称的。(节点1的邻居的度为2和3,节点2的邻居的度为2和3,即使我们继续深入到2-hop的邻居,节点都是相同度)
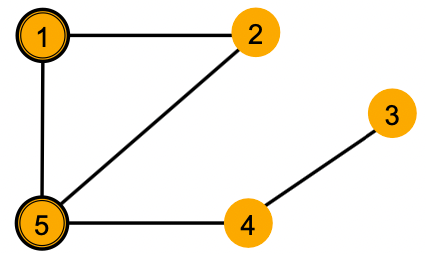
关键问题:GNN节点嵌入能够区分不同节点的局部邻域结构吗?
如果是这样,什么时候?如果没有,什么时候GNN会失败?
接下来,我们需要理解GNN如何捕获局部邻域结构。关键概念:计算图。
计算图
在每层,GNN聚合邻居节点嵌入。
GNN通过一个由邻域定义的计算图生成节点嵌入。
如:节点1和2的计算图(2层GNN),但是GNN只能得到节点特征,而不是IDs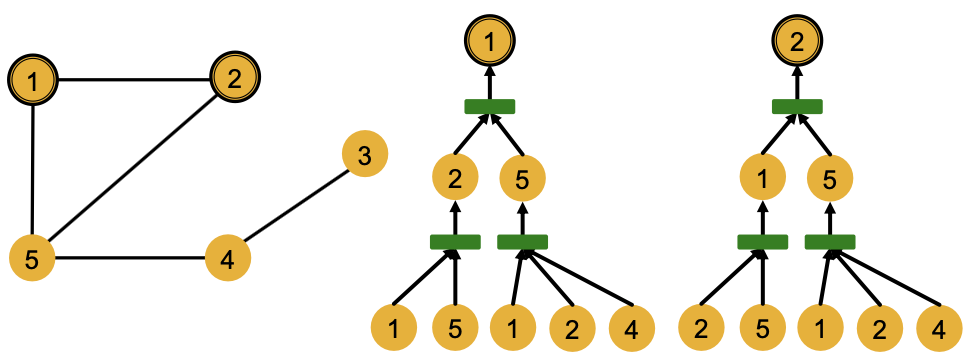
GNN会对节点1和2生成相同的嵌入,这是因为:
- 计算图是相同的
- 节点特征(颜色)是相同的
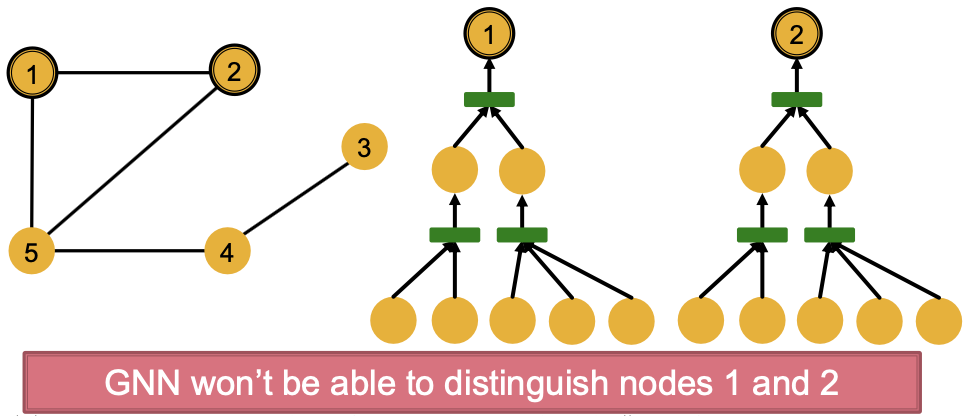
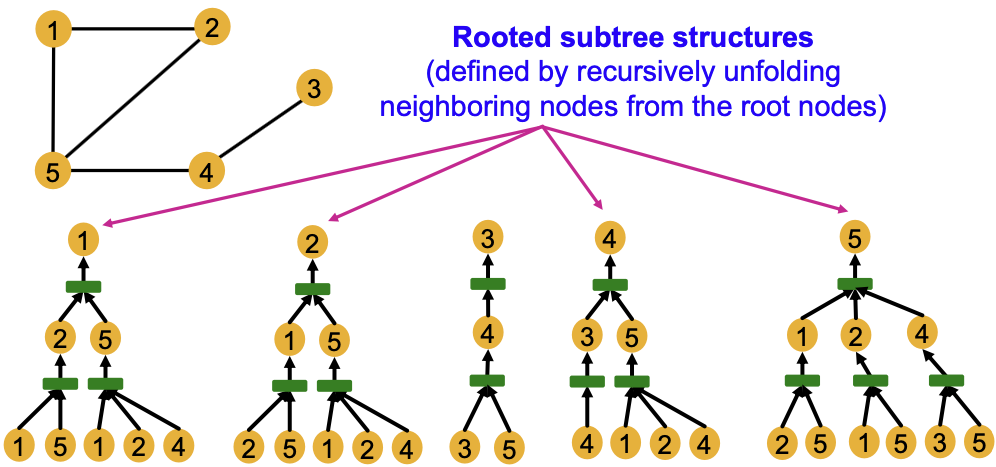
一般来说,不同局部邻域定义不同计算图。
- 计算图与每个节点周围的根子树结构相同。
- GNN节点嵌入捕获根子树结构。
- 大多数表达性GNN将不同的根子树映射到不同的节点嵌入(用不同的颜色表示)。
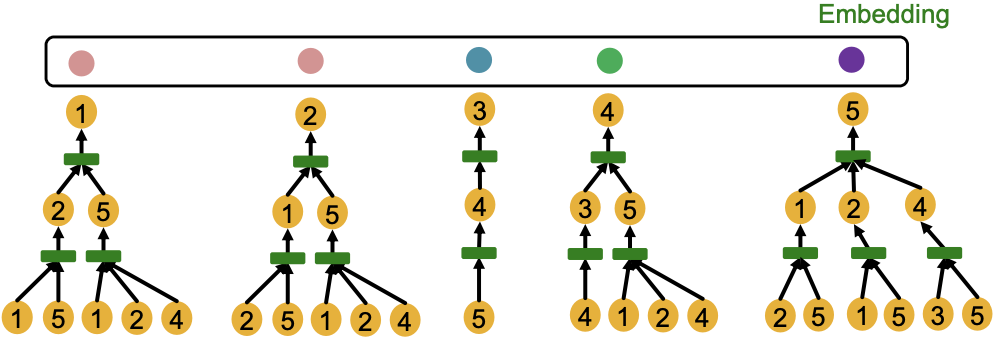
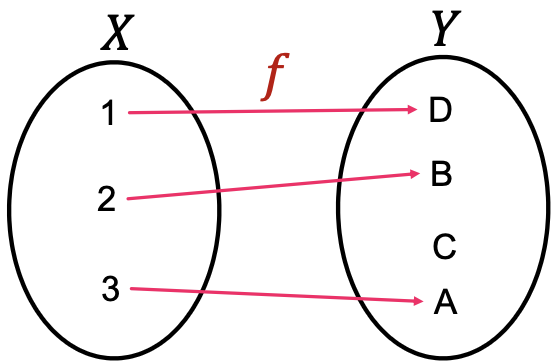
回顾内射(injective)函数:
- 函数
是内射,若它将不同元素映射到不同输出
- 直观上,
保留所有关于输入的信息
GNN的表达能力如何?
最具表现力的GNN应该是单射地将子树映射到节点嵌入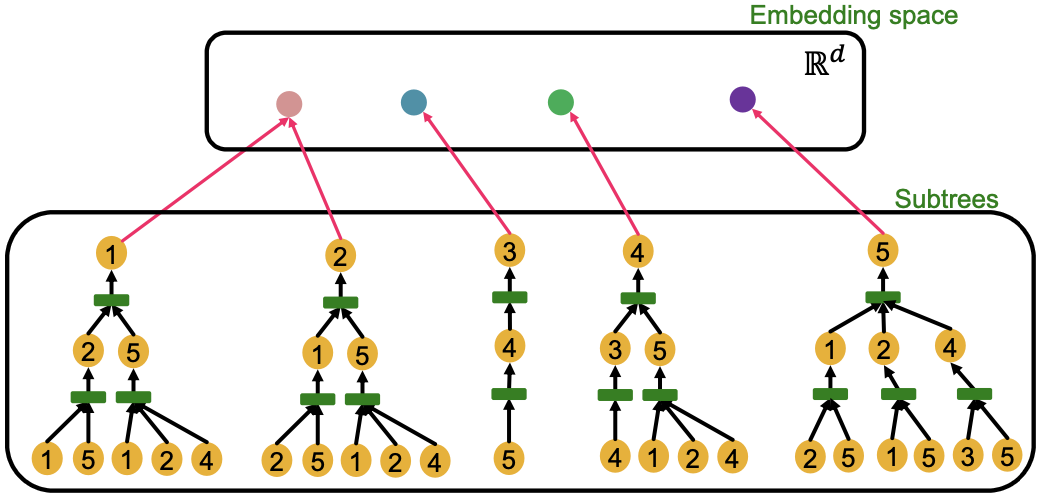
关键点:相同深度的子树可以从叶节点递归地表征到根节点。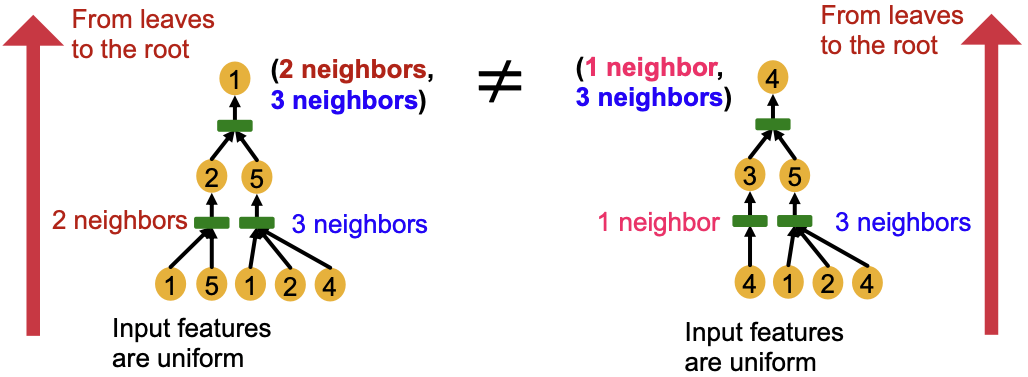
如果GNN的每一步聚合都能充分保留相邻信息,则生成的节点嵌入可以区分不同的根树。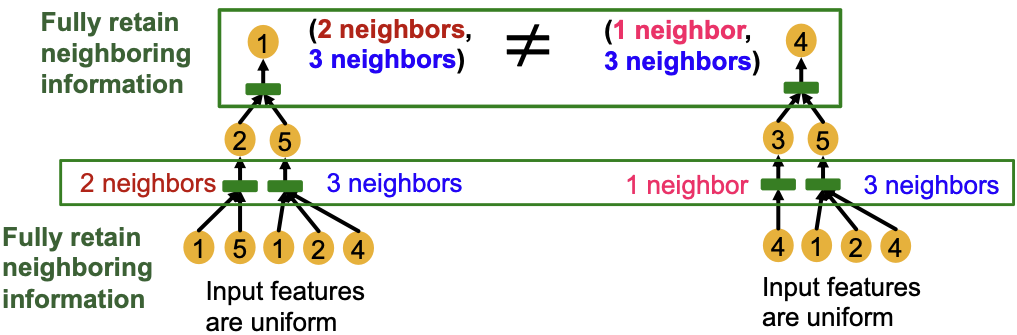
换句话说,最有表现力的GNN将在每一步使用一个单射邻居聚合函数。将不同的邻居映射到不同的嵌入。
Summary
为了生成节点嵌入,GNN使用一个计算图,对应于围绕每个节点根的子树。
如果近邻聚合的每一步都是单射的,那么GNN可以完全区分不同的子树结构。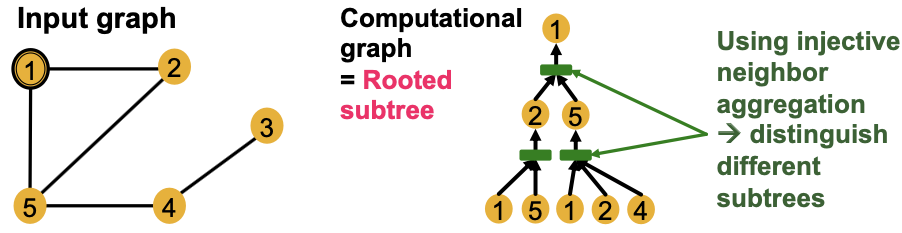
Designing the Most Powerful Graph Neural Network
GNN的表达能力:
关键点:GNN的表达能力可以通过其使用的邻居聚合函数来表征。
- 一个表达能力更强的聚合函数会导致一个表达能力更强的GNN。
- 单射聚合函数(injective aggregation function)导致最具表现力的GNN。
邻居聚合
邻居聚合可以被抽象为一个多集合(包含重复元素的集合)上的函数。
接下来,我们分析两个流行的GNN模型的聚合函数:
- GCN (mean pool) [Kipf & Welling, ICLR 2017]
- 对邻居节点特征使用 element-wise 平均池化,
- 接下来是线性函数和ReLU激活,即
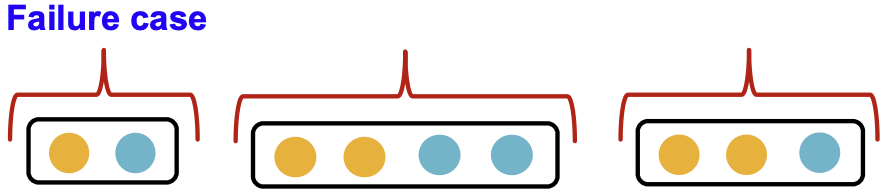
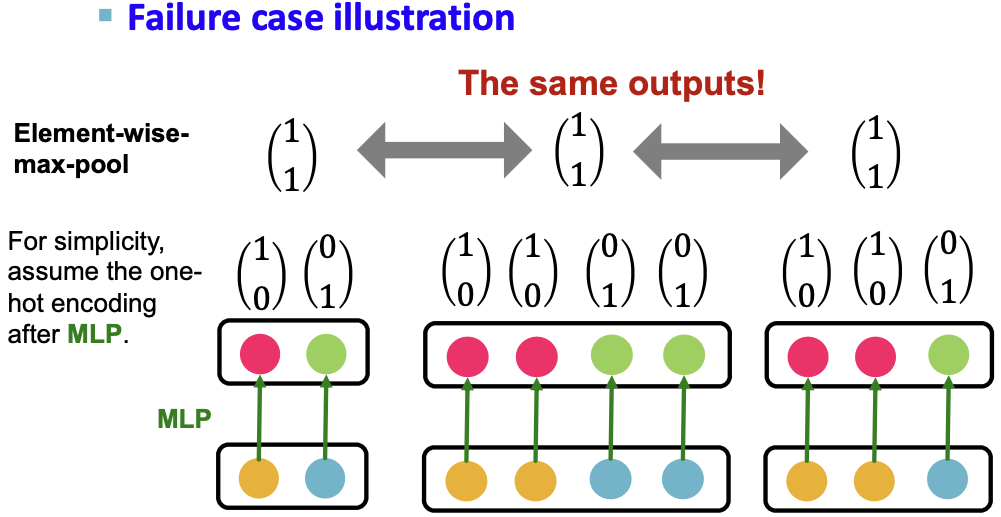
- Theorem [Xu et al. ICLR 2019]:GCN的聚合函数不能区分具有相同颜色比例的不同多集。
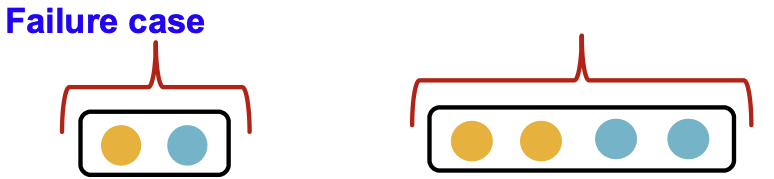
- 为了简单起见,假设节点颜色使用one-hot编码,例如两个不同的颜色:

- 这个假设足以说明GCN是如何失败的。
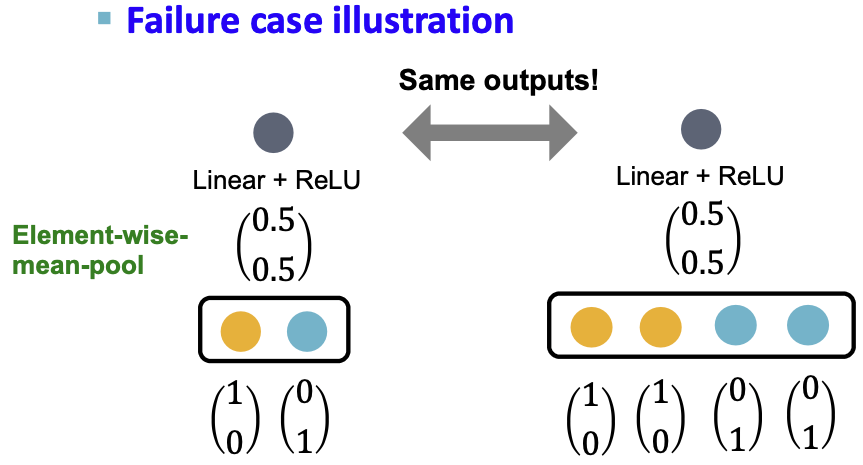
- 对邻居节点特征使用 element-wise 平均池化,
GraphSAGE (max-pool) [Hamiton et al. NeurIPS 2017]
GNN的表达能力可以用邻居聚合函数的表达能力来表征;
- 邻居聚合是多集合(包含重复元素的集合)上的函数;
- GCN和GraphSAGE的聚合函数不能区分一些基本的多集,因此不内射;
-
设计最有表达力的GNNs
目标:在消息传递GNN类中设计最强大的GNN
这可以通过设计多集合上的单射邻居聚合函数来实现,在此我们设计了一个可以建模单射多集函数(injective multiset function)的神经网络。Injective Multi-Set Function
Theorem [Xu et al. ICLR 2019]
任何单射多集函数都可以表示为: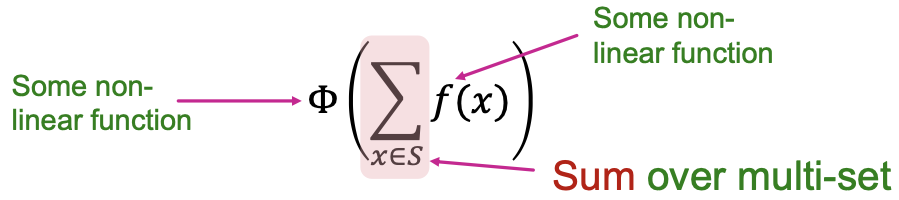

证明:产生一个one-hot编码的颜色,对one-hot编码的求和保留了输入多集的所有信息。
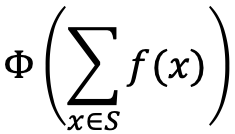
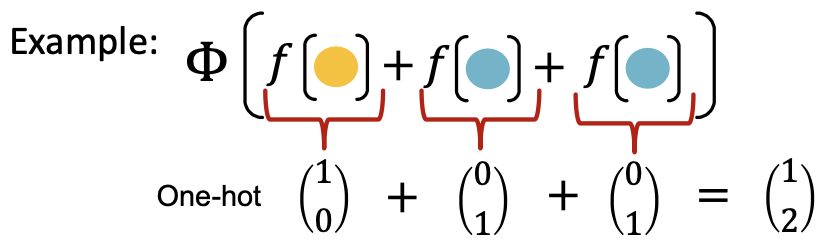
通用逼近定理
在
中如何拟合
和
?使用一个Multi-Layer Perceptron(MLP)。
Theorem Universal Approximation Theorem [Hornik et al., 1989] :
具有足够大隐维数和适当非线性𝜎(包括ReLU和sigmoid)的1-隐层MLP可近似任意精度的任意连续函数。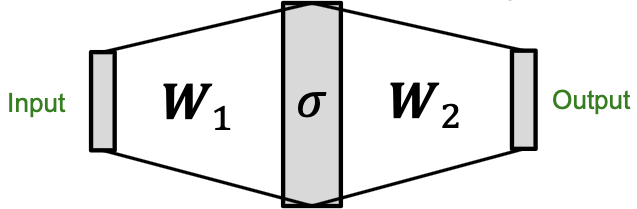
我们得到了一个可以拟合任何单射多集函数的神经网络:
在实践中,MLP隐藏维度为100到500就足够了。GIN
Graph Isomorphim Network (GIN, 图同构网络) [Xu et al. ICLR 2019]
应用一个MLP,按元素求和,然后是另一个MLP。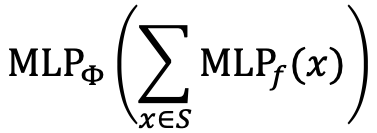
GIN的邻居聚合函数是单射的,没有失败的例子!GIN在消息传递GNNs中是最有表达力的GNN!
到目前为止,我们介绍了GIN的邻居聚合部分,接下来我们将介绍GIN的全部内容,通过将其与WL graph kernel联系起来(获得graph-level特征的经典方式),我们将看到GIN是一个“神经网络”版本的WL graph kernel。Relation to WL Graph Kernel
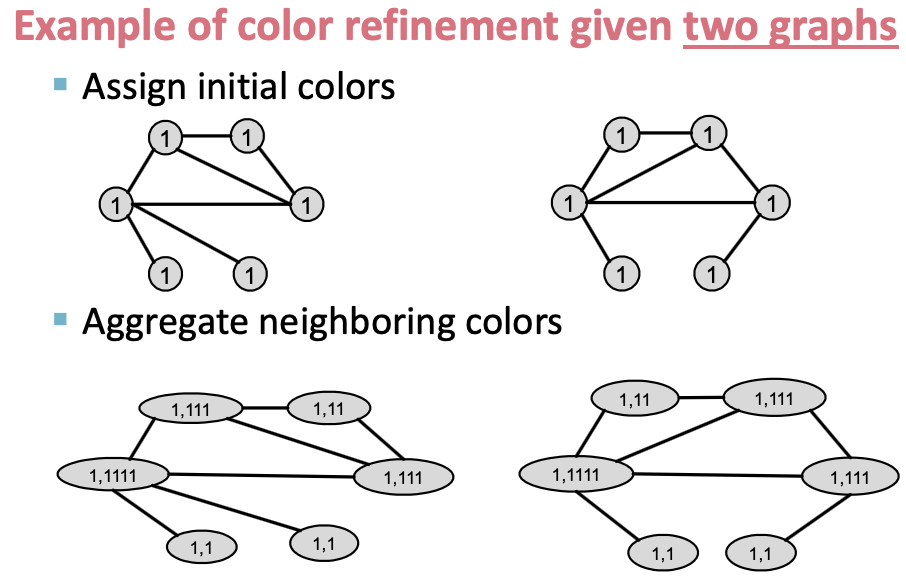
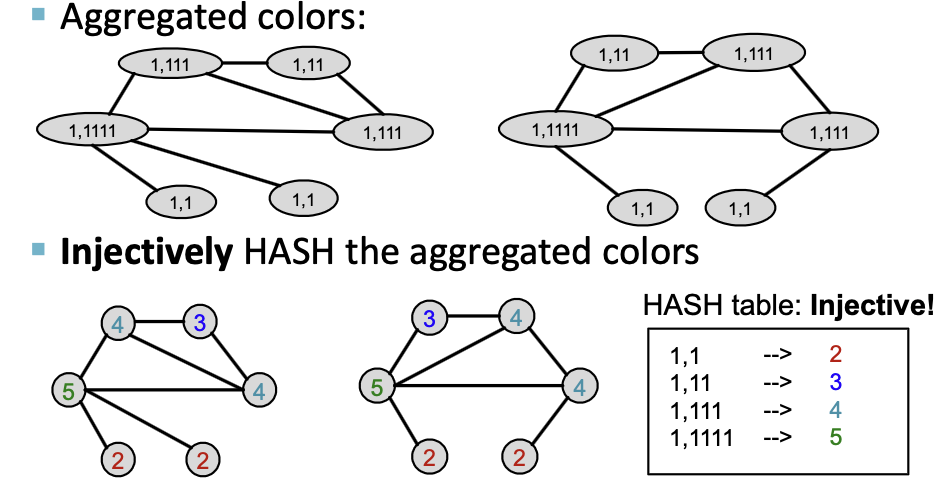
color refinement algorithm
回顾:在WL kernel中的颜色优化算法(color refinement algorithm)
给定一个节点集合为的图
:
给每个节点
分配初始颜色
;
- 根据
,其中 HASH 将不同输入映射为不同颜色,迭代优化节点颜色;
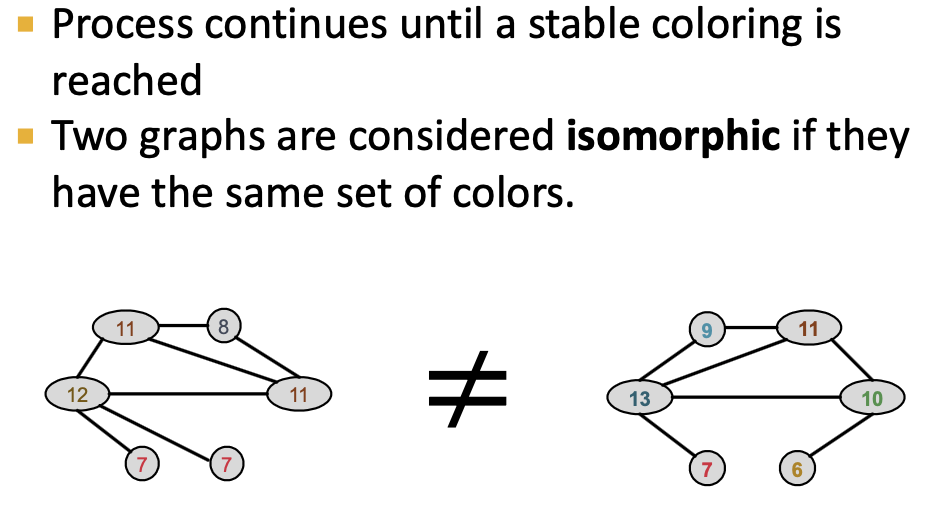
- K步颜色优化之后,
总结了𝐾-hop邻域的结构。
The Complete GIN Model
GIN使用一个神经网络来拟合单射HASH函数: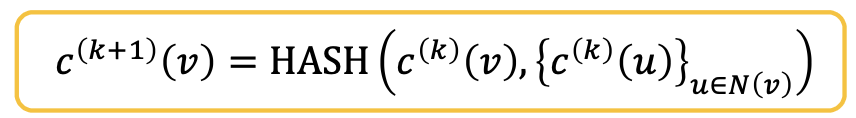
特别地,我们将在元组上拟合单射函数:
理论 [Xu et al. ICLR 2019]:
元组上的任何单射函数 可被拟合为
可被拟合为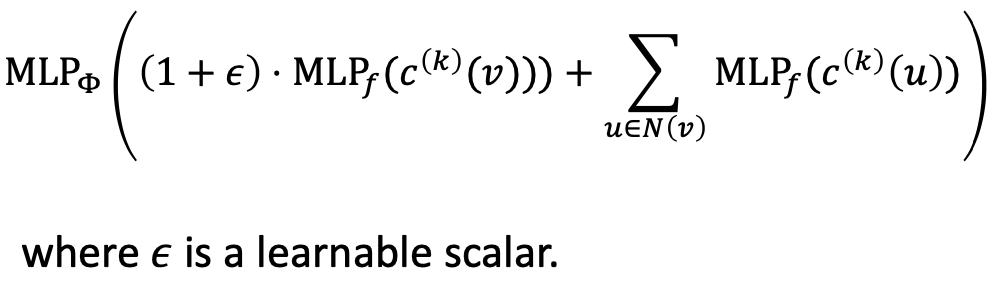
若输入特征被表示为one-hot,则直接加和是单射的。
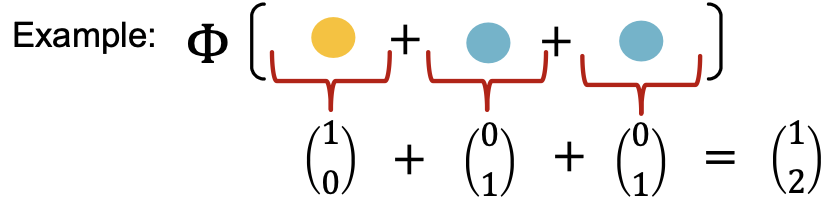
我们仅需要来保证单射:
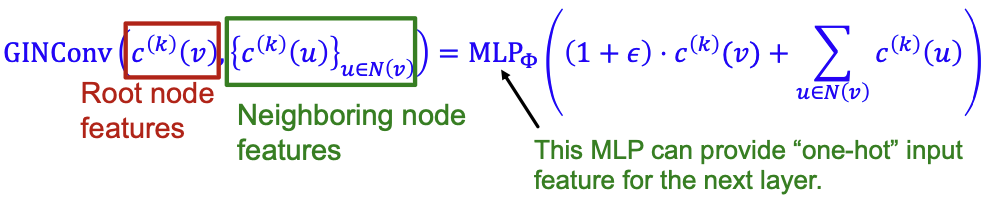
GIN节点嵌入的更新:
- 给每个节点
分配初始向量
;
- 迭代更新节点向量,
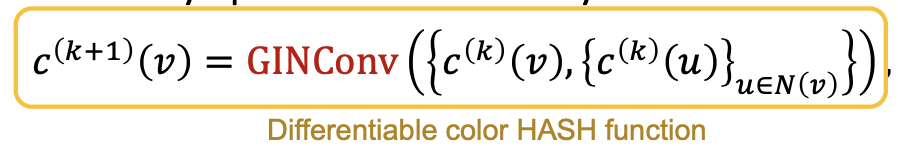 ,其中 GINConv 将不同输入映射到不同嵌入;
,其中 GINConv 将不同输入映射到不同嵌入; -
GIN and WL Graph Kernel
GIN可以理解为 WL Graph Kernel 的可区分的神经网络版本:

GIN相对于WL图核的优势有: 节点嵌入是低维的,因此能够捕获不同节点的细粒度相似性。
- 为了下游任务,更新函数的参数能够学习到。
由于GIN和WL图核之间的关系,它们的表达方式完全相同。如果两个图可以用GIN来区分,那么它们也可以用WL内核来区分,反之亦然。
这有多强大?
- WL内核在理论和经验上都被证明可以区分大多数真实世界的图 [Cai et al. 1992]
-
Summary
设计了一个神经网络,能够拟合单射多集函数;
- 使用神经网络作为邻居聚集函数,得到了最具表现力的GNN模型GIN;
- 关键是使用element-wise加和池化,而不是平均/最大池化;
- GIN与WL图内核密切相关;
- GIN和WL图核都可以区分大多数真实的图形!

提高GNN的表达能力:
有一些基本的图结构是现有GNN框架无法区分的,比如循环中的差异。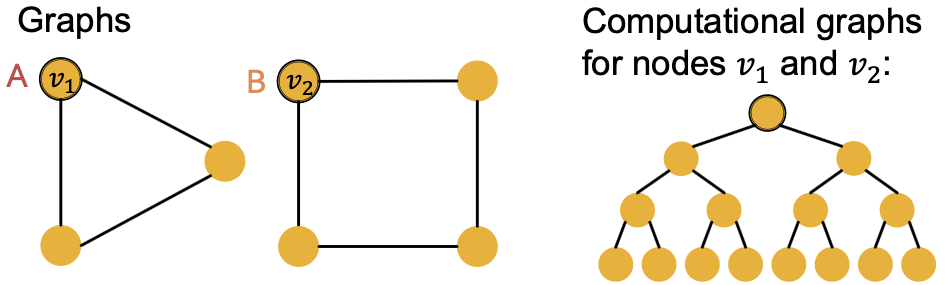
为了解决上述问题,可以提高GNNs的表达能力。[You et al. AAAI 2021, Li et al. NeurlPS 2020]