图的传统ML：给定一个输入图，提取节点、链接和图级的特征，学习一个将特征映射为标签的模型(SVM、神经网络等)。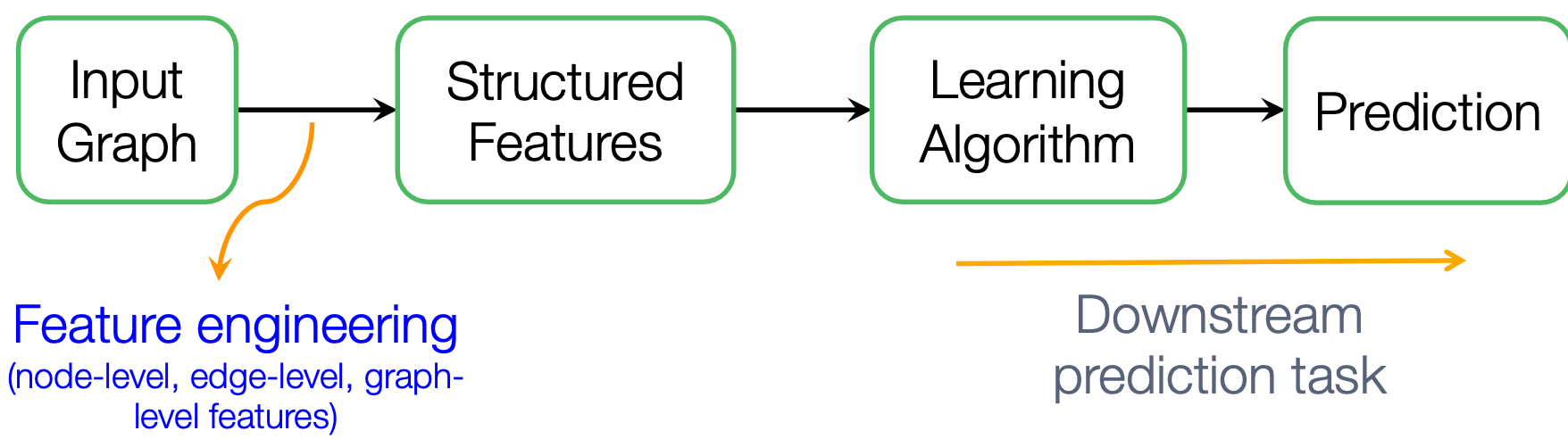
image.png
图表示学习：减轻了每一次进行特征工程的需要。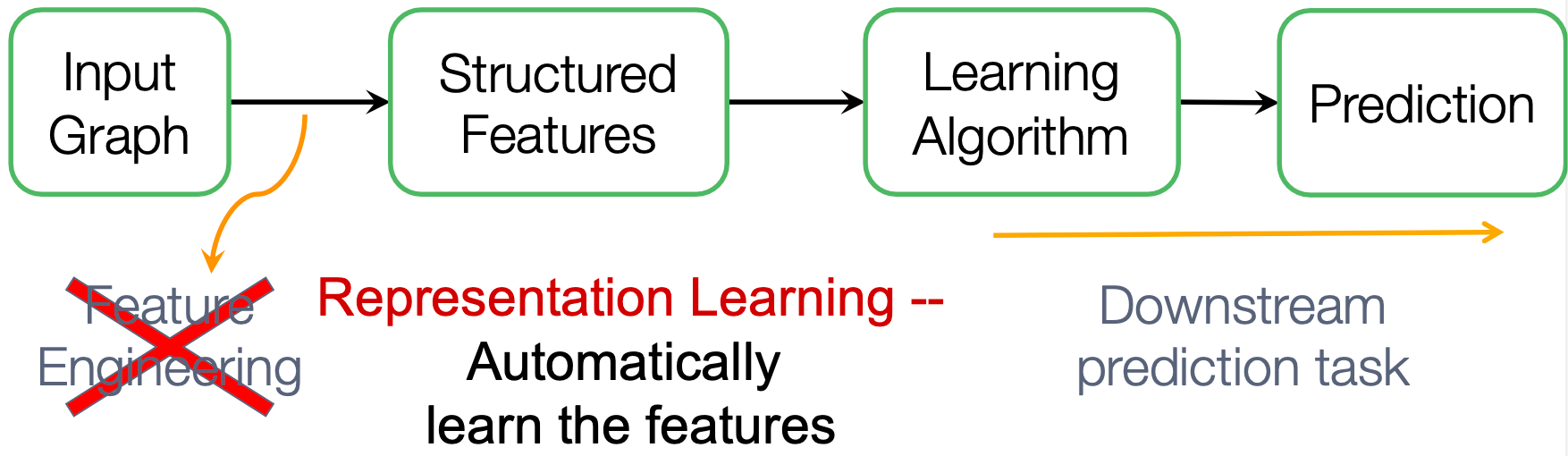
image.png
目标：基于图机器学习的高效独立任务的特征学习!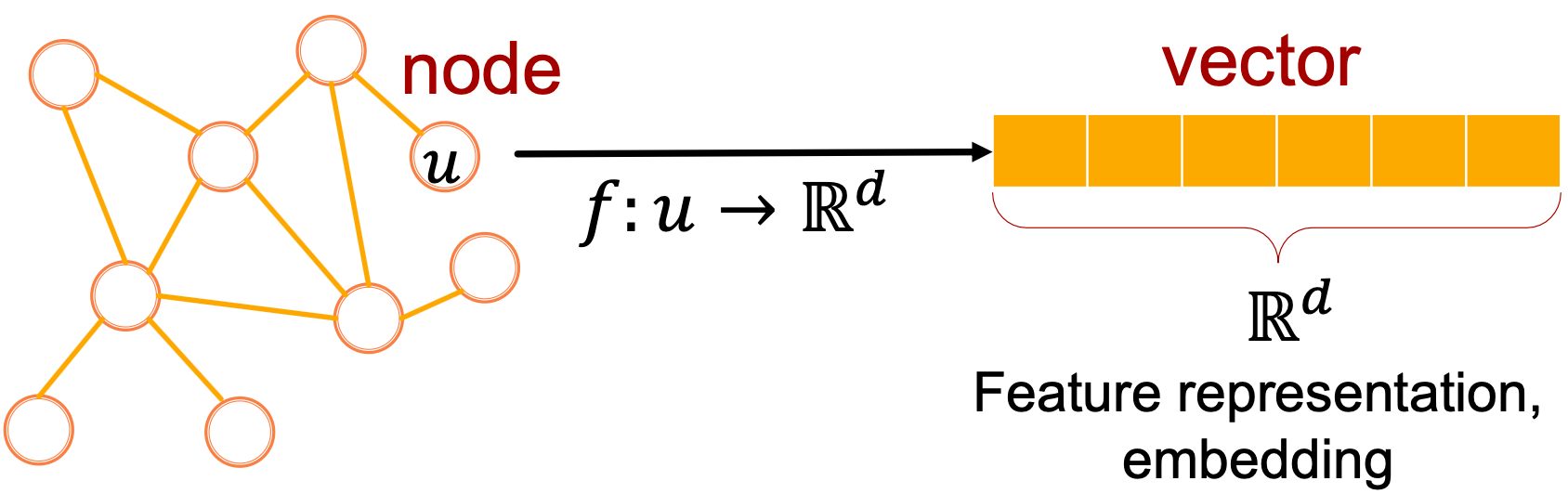
image.png
Why Embedding?
任务：将节点映射到嵌入空间。

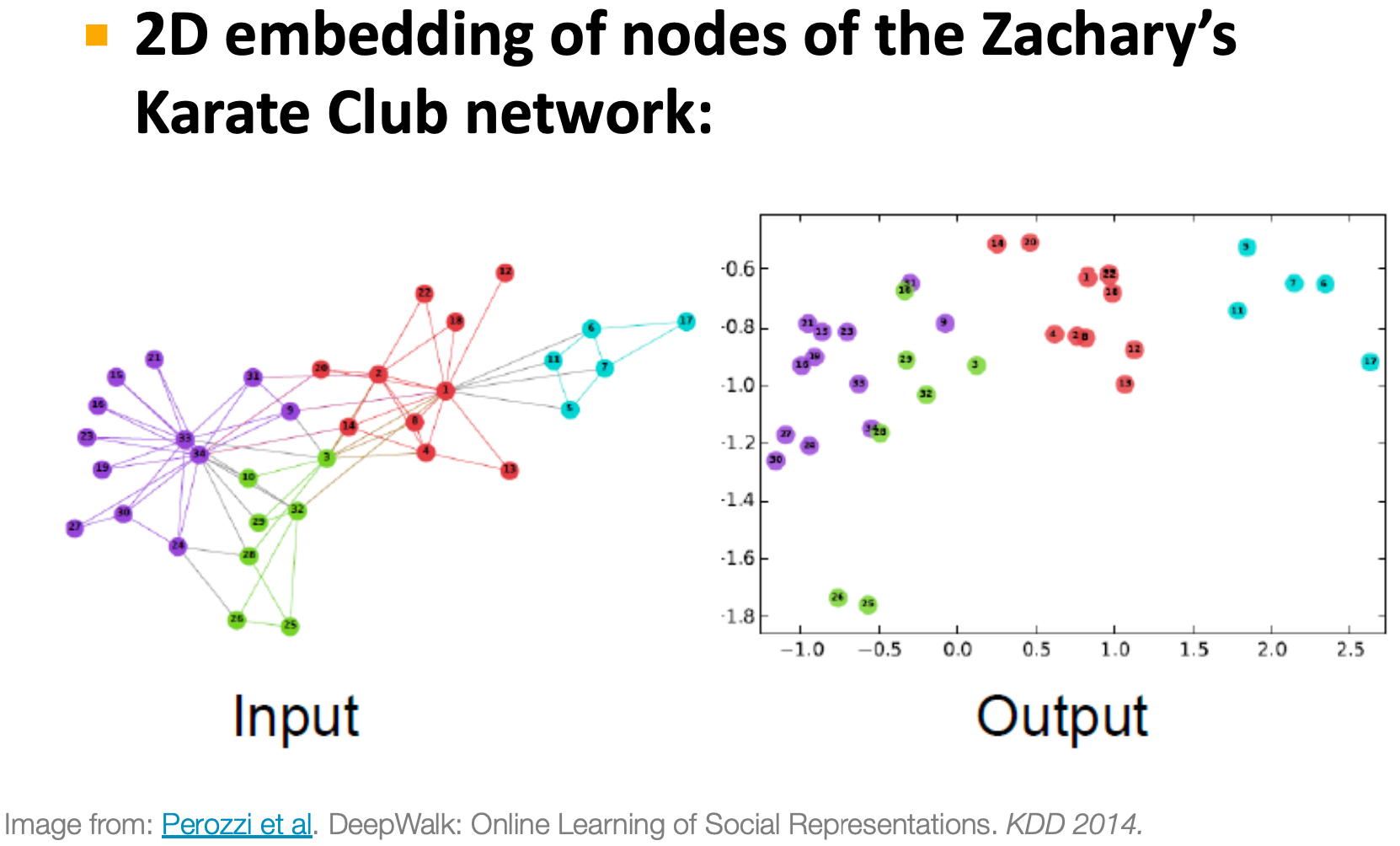
  • 节点间嵌入的相似性表明节点之间在网络中的相似性。例如：两个节点彼此靠近(由一条边连接)。
  • 编码网络信息
  • 可用于许多下游预测

image.png
节点嵌入例子：
image.png

Node Embeddings: Encoder and Decoder

假设图03 Node Embeddings - 图6的顶点集03 Node Embeddings - 图7、二元邻接矩阵03 Node Embeddings - 图8.
目标是对节点进行编码，使嵌入空间的相似性(例如，点积)近似于图中的相似性。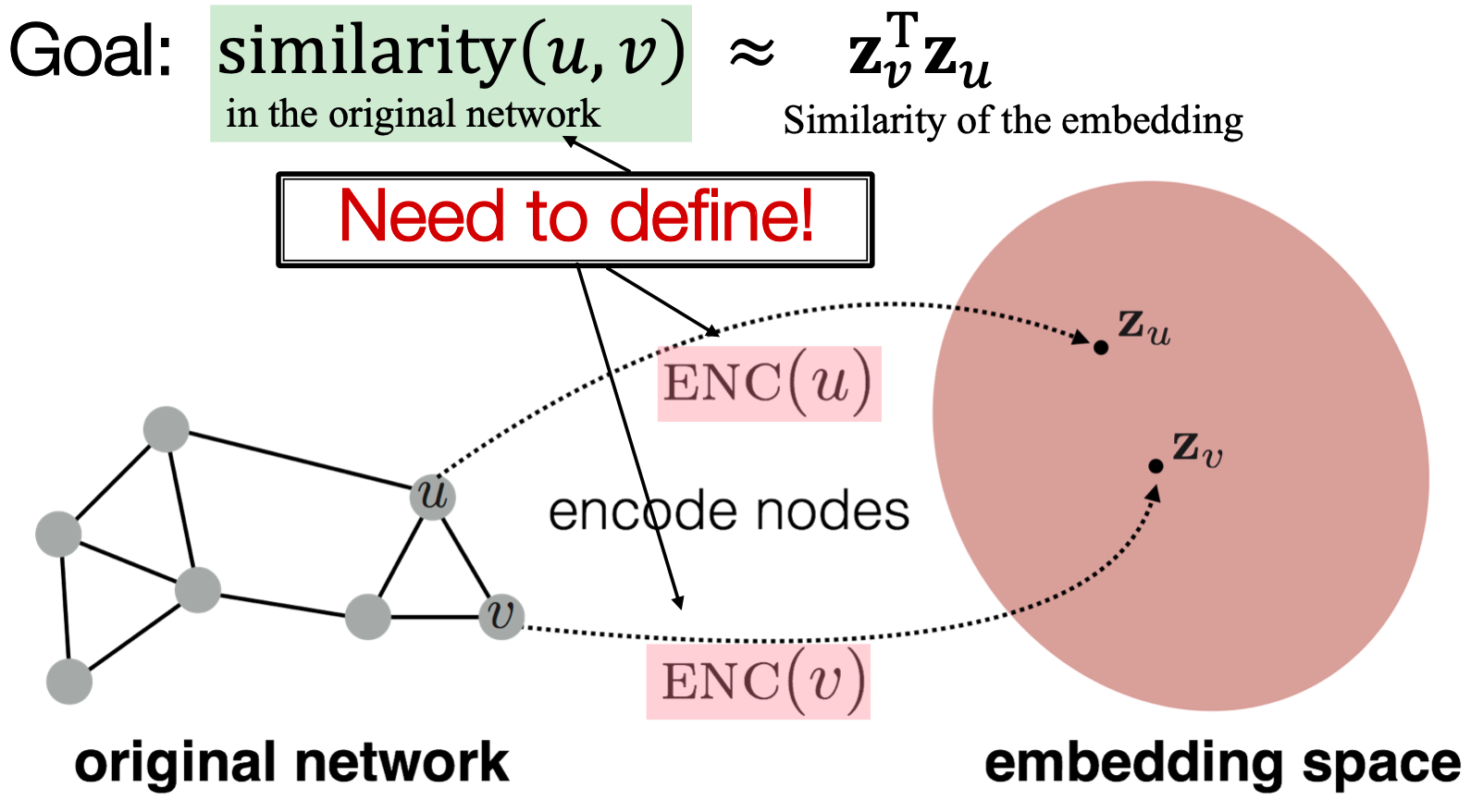
image.png
学习节点嵌入：

  1. encoder从节点映射到嵌入；
  2. 定义一个节点相似函数(即，原始网络中相似度的度量)；
  3. Decoder DEC从嵌入映射到相似度评分；
  4. 优化encoder参数，使：

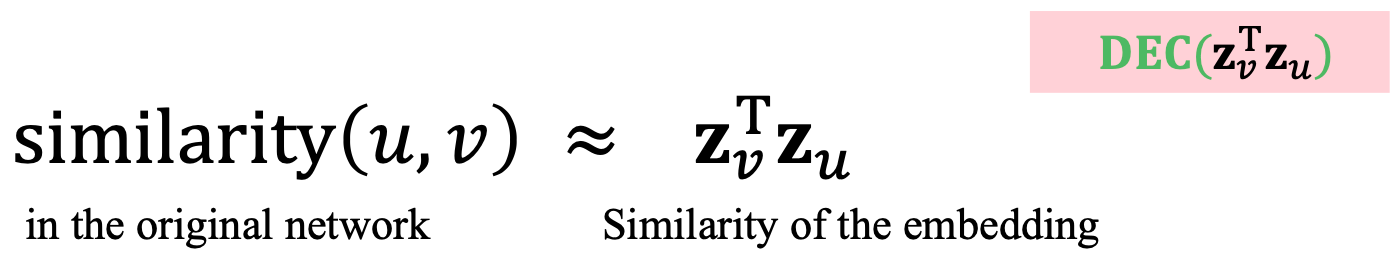
image.png
两个关键点：

  • encoder：将每个节点映射为低维向量

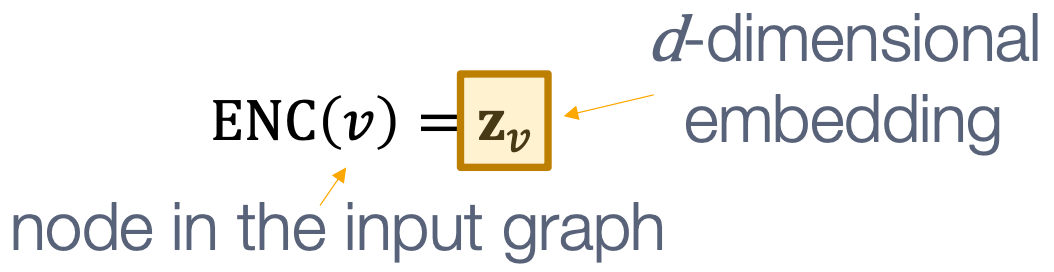
image.png

  • 相似函数：指定向量空间中的关系如何映射到原始网络中的关系

image.png
最简单的encoding方法是：encoder只是一个embedding-lookup，shallow encoder。
image.png
image.png
每个节点被分配一个唯一的嵌入向量(即直接优化每个节点的嵌入)。
这类有许多方法，如Deepwalk、node2vec等。

Encoder + Decoder 框架总结

  • shallow encoder：embedding lookup
  • 优化参数：对于所有节点03 Node Embeddings - 图15，03 Node Embeddings - 图16包含节点嵌入03 Node Embeddings - 图17
  • 我们将在第6讲中介绍深层编码器(GNNs)
  • decoder：基于节点相似性

  • objective：最大化03 Node Embeddings - 图18，节点对03 Node Embeddings - 图19是相似的

    如何定义节点的相似性？

  • 方法的关键选择是如何定义节点相似性。

  • 两个节点是否有相似的嵌入，如果它们linked、共享邻居、有类似的“结构角色”？

  • 现在我们将学习使用随机游走（random walks）的节点相似度定义，以及如何为这种相似度度量优化嵌入。

    note

  • 这是无监督/半监督的节点嵌入学习方法，不使用节点标签、节点特征，目标是直接估计节点的一组坐标（如嵌入），以便保留网络结构的某些方面（由DEC捕获）；

  • 这些嵌入是独立于任务，它们没有接受过特定任务的训练但却可以用于任何任务。

    Random Walk Approaches for Node Embeddings

    记号

  • 向量03 Node Embeddings - 图20：节点03 Node Embeddings - 图21的嵌入（我们要找的目标）；

  • 概率03 Node Embeddings - 图22：从节点03 Node Embeddings - 图23开始随机遍历访问节点03 Node Embeddings - 图24的(预测)概率（我们模型预测是基于03 Node Embeddings - 图25）

用于产生预测概率的非线性函数：

  • Softmax函数：将03 Node Embeddings - 图26的真实值(模型预测)转换为03 Node Embeddings - 图27的概率，总和为1：03 Node Embeddings - 图28；

  • Sigmoid函数：s形函数，将实值转换为(0,1)范围，写为03 Node Embeddings - 图29。

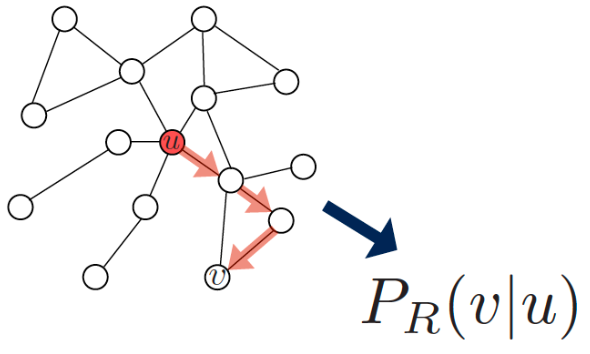
    Random Walk

    给定一个图和一个起始点，我们随机选择它的一个邻居，然后移动到这个邻居；然后我们随机选择这个点的一个邻居，然后向它移动，以此类推。用这种方法访问的(随机)点序列是图上的随机游走（Random Walk）。
    random-walk embeddings：
    image.pngu和v在图上随机遍历时同时出现的概率

    Random-Walk Embeddings

  • 使用随机游走策略03 Node Embeddings - 图31从节点03 Node Embeddings - 图32开始随机游走，估计访问节点03 Node Embeddings - 图33的概率：

image.png

  • 优化嵌入以编码这些随机游走统计数据：嵌入空间的相似性编码随机游走“相似性”(这里:点积=cos(𝜃))

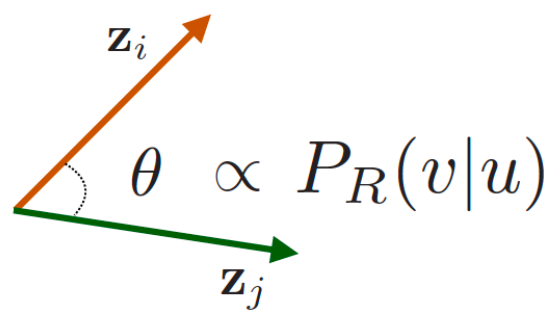
image.png
Random Walks优点：

  • 可表达性：节点相似度的灵活随机定义，包含局部和高阶邻域信息；思想：如果从节点03 Node Embeddings - 图36以高概率访问03 Node Embeddings - 图37开始随机行走，03 Node Embeddings - 图38和03 Node Embeddings - 图39相似(高阶多跳信息)；
  • 效率：训练时不需要考虑所有节点对；只需要考虑在随机游动中同时出现的对。

无监督特征学习：

  • 直觉：在03 Node Embeddings - 图40维空间中找到保留相似性的节点嵌入；
  • 思想：学习节点嵌入，使相邻的节点在网络中紧密相连；
  • 给定一个节点03 Node Embeddings - 图41，我们如何定义附近的节点？03 Node Embeddings - 图42由某种随机游走策略03 Node Embeddings - 图43得到03 Node Embeddings - 图44的邻域。

作为优化的特征学习：

  • 给定03 Node Embeddings - 图45，我们目标是学习一个映射03 Node Embeddings - 图46
  • log-likelihood objective：03 Node Embeddings - 图47, 03 Node Embeddings - 图48是节点03 Node Embeddings - 图49通过策略03 Node Embeddings - 图50的邻域
  • 给定节点03 Node Embeddings - 图51，我们想要学习特征表示，这些特征表示可以预测其随机游走邻域03 Node Embeddings - 图52中的节点

    随机游走优化

  1. 从图中的每个节点03 Node Embeddings - 图53开始，使用随机游走策略03 Node Embeddings - 图54执行固定长度的短随机游走；
  2. 对于每个节点03 Node Embeddings - 图55收集03 Node Embeddings - 图56，从03 Node Embeddings - 图57开始随机游走访问多个节点集；
  3. 优化嵌入：给定节点03 Node Embeddings - 图58，预测其邻居03 Node Embeddings - 图59，03 Node Embeddings - 图60。

03 Node Embeddings - 图61可以有重复的元素，因为节点可以在随机游走中被访问多次。
等价地，03 Node Embeddings - 图62
直觉：优化嵌入03 Node Embeddings - 图63，以最大限度地提高随机游走同时出现的可能性
使用softmax参数化03 Node Embeddings - 图64：03 Node Embeddings - 图65
为什么softmax？我们希望节点03 Node Embeddings - 图66与节点03 Node Embeddings - 图67(在所有节点03 Node Embeddings - 图68中)最相似。直觉：03 Node Embeddings - 图69
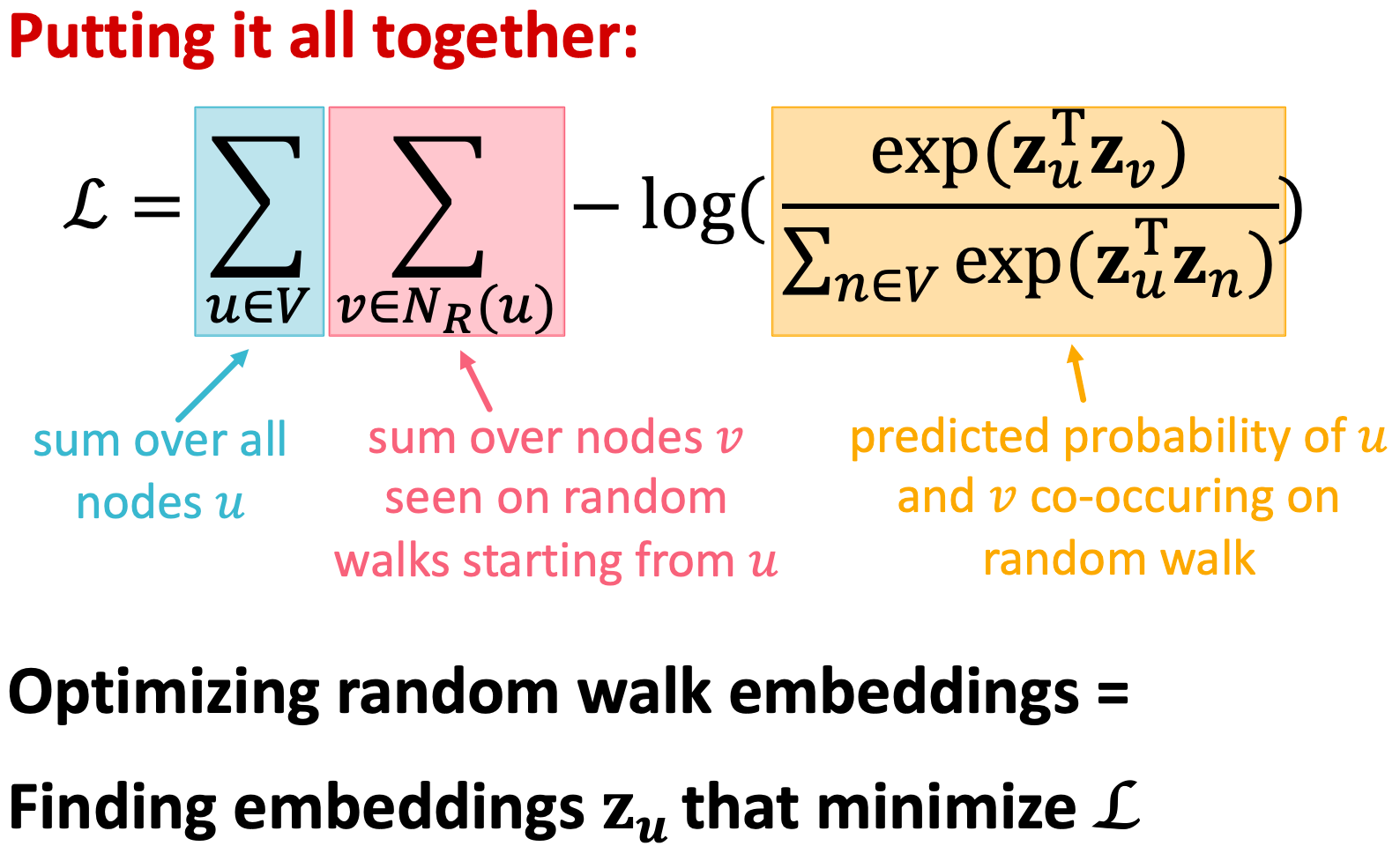
image.png
但是这样做代价太高！嵌入的节点求和得到03 Node Embeddings - 图71复杂度！
来自softmax的标准化项03 Node Embeddings - 图72是罪魁祸首…我们能近似一下吗？
解决方法：Negative sampling 负采样
为什么近似是有效的？从技术上讲，这是一个不同的目标，但负采样是一种噪声对比估计(Noise Contrastive Estimation, NCE)的形式，它近似地最大化了softmax的对数概率。新的公式对应于使用逻辑回归(sigmoid func.)来区分目标节点03 Node Embeddings - 图73和从分布03 Node Embeddings - 图74 中采样的节点03 Node Embeddings - 图75。更多见https://arxiv.org/pdf/1402.3722.pdf
image.png
抽样03 Node Embeddings - 图77个负节点，每个节点的概率与其度成正比。
03 Node Embeddings - 图78的两个考虑因素(#负样本)：

  • 更高的03 Node Embeddings - 图79给出了更可靠的估计；
  • 03 Node Embeddings - 图80越高，对负面事件的偏见就越高。

在实践中，03 Node Embeddings - 图81。

Stochastic Gradient Descent

我们获得目标函数03 Node Embeddings - 图82%7D-%5Clog%20(P(v%7Czu))%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJCAL-4C%22%20d%3D%22M62%20-22T47%20-22T32%20-11Q32%20-1%2056%2024T83%2055Q113%2096%20138%20172T180%20320T234%20473T323%20609Q364%20649%20419%20677T531%20705Q559%20705%20578%20696T604%20671T615%20645T618%20623V611Q618%20582%20615%20571T598%20548Q581%20531%20558%20520T518%20509Q503%20509%20503%20520Q503%20523%20505%20536T507%20560Q507%20590%20494%20610T452%20630Q423%20630%20410%20617Q367%20578%20333%20492T271%20301T233%20170Q211%20123%20204%20112L198%20103L224%20102Q281%20102%20369%2079T509%2052H523Q535%2064%20544%2087T579%20128Q616%20152%20641%20152Q656%20152%20656%20142Q656%20101%20588%2040T433%20-22Q381%20-22%20289%201T156%2028L141%2029L131%2020Q111%200%2087%20-11Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ2-2211%22%20d%3D%22M60%20948Q63%20950%20665%20950H1267L1325%20815Q1384%20677%201388%20669H1348L1341%20683Q1320%20724%201285%20761Q1235%20809%201174%20838T1033%20881T882%20898T699%20902H574H543H251L259%20891Q722%20258%20724%20252Q725%20250%20724%20246Q721%20243%20460%20-56L196%20-356Q196%20-357%20407%20-357Q459%20-357%20548%20-357T676%20-358Q812%20-358%20896%20-353T1063%20-332T1204%20-283T1307%20-196Q1328%20-170%201348%20-124H1388Q1388%20-125%201381%20-145T1356%20-210T1325%20-294L1267%20-449L666%20-450Q64%20-450%2061%20-448Q55%20-446%2055%20-439Q55%20-437%2057%20-433L590%20177Q590%20178%20557%20222T452%20366T322%20544L56%20909L55%20924Q55%20945%2060%20948Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-75%22%20d%3D%22M21%20287Q21%20295%2030%20318T55%20370T99%20420T158%20442Q204%20442%20227%20417T250%20358Q250%20340%20216%20246T182%20105Q182%2062%20196%2045T238%2027T291%2044T328%2078L339%2095Q341%2099%20377%20247Q407%20367%20413%20387T427%20416Q444%20431%20463%20431Q480%20431%20488%20421T496%20402L420%2084Q419%2079%20419%2068Q419%2043%20426%2035T447%2026Q469%2029%20482%2057T512%20145Q514%20153%20532%20153Q551%20153%20551%20144Q550%20139%20549%20130T540%2098T523%2055T498%2017T462%20-8Q454%20-10%20438%20-10Q372%20-10%20347%2046Q345%2045%20336%2036T318%2021T296%206T267%20-6T233%20-11Q189%20-11%20155%207Q103%2038%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2208%22%20d%3D%22M84%20250Q84%20372%20166%20450T360%20539Q361%20539%20377%20539T419%20540T469%20540H568Q583%20532%20583%20520Q583%20511%20570%20501L466%20500Q355%20499%20329%20494Q280%20482%20242%20458T183%20409T147%20354T129%20306T124%20272V270H568Q583%20262%20583%20250T568%20230H124V228Q124%20207%20134%20177T167%20112T231%2048T328%207Q355%201%20466%200H570Q583%20-10%20583%20-20Q583%20-32%20568%20-40H471Q464%20-40%20446%20-40T417%20-41Q262%20-41%20172%2045Q84%20127%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-56%22%20d%3D%22M52%20648Q52%20670%2065%20683H76Q118%20680%20181%20680Q299%20680%20320%20683H330Q336%20677%20336%20674T334%20656Q329%20641%20325%20637H304Q282%20635%20274%20635Q245%20630%20242%20620Q242%20618%20271%20369T301%20118L374%20235Q447%20352%20520%20471T595%20594Q599%20601%20599%20609Q599%20633%20555%20637Q537%20637%20537%20648Q537%20649%20539%20661Q542%20675%20545%20679T558%20683Q560%20683%20570%20683T604%20682T668%20681Q737%20681%20755%20683H762Q769%20676%20769%20672Q769%20655%20760%20640Q757%20637%20743%20637Q730%20636%20719%20635T698%20630T682%20623T670%20615T660%20608T652%20599T645%20592L452%20282Q272%20-9%20266%20-16Q263%20-18%20259%20-21L241%20-22H234Q216%20-22%20216%20-15Q213%20-9%20177%20305Q139%20623%20138%20626Q133%20637%2076%20637H59Q52%20642%2052%20648Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-76%22%20d%3D%22M173%20380Q173%20405%20154%20405Q130%20405%20104%20376T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Q21%20294%2029%20316T53%20368T97%20419T160%20441Q202%20441%20225%20417T249%20361Q249%20344%20246%20335Q246%20329%20231%20291T200%20202T182%20113Q182%2086%20187%2069Q200%2026%20250%2026Q287%2026%20319%2060T369%20139T398%20222T409%20277Q409%20300%20401%20317T383%20343T365%20361T357%20383Q357%20405%20376%20424T417%20443Q436%20443%20451%20425T467%20367Q467%20340%20455%20284T418%20159T347%2040T241%20-11Q177%20-11%20139%2022Q102%2054%20102%20117Q102%20148%20110%20181T151%20298Q173%20362%20173%20380Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4E%22%20d%3D%22M234%20637Q231%20637%20226%20637Q201%20637%20196%20638T191%20649Q191%20676%20202%20682Q204%20683%20299%20683Q376%20683%20387%20683T401%20677Q612%20181%20616%20168L670%20381Q723%20592%20723%20606Q723%20633%20659%20637Q635%20637%20635%20648Q635%20650%20637%20660Q641%20676%20643%20679T653%20683Q656%20683%20684%20682T767%20680Q817%20680%20843%20681T873%20682Q888%20682%20888%20672Q888%20650%20880%20642Q878%20637%20858%20637Q787%20633%20769%20597L620%207Q618%200%20599%200Q585%200%20582%202Q579%205%20453%20305L326%20604L261%20344Q196%2088%20196%2079Q201%2046%20268%2046H278Q284%2041%20284%2038T282%2019Q278%206%20272%200H259Q228%202%20151%202Q123%202%20100%202T63%202T46%201Q31%201%2031%2010Q31%2014%2034%2026T39%2040Q41%2046%2062%2046Q130%2049%20150%2085Q154%2091%20221%20362L289%20634Q287%20635%20234%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-52%22%20d%3D%22M230%20637Q203%20637%20198%20638T193%20649Q193%20676%20204%20682Q206%20683%20378%20683Q550%20682%20564%20680Q620%20672%20658%20652T712%20606T733%20563T739%20529Q739%20484%20710%20445T643%20385T576%20351T538%20338L545%20333Q612%20295%20612%20223Q612%20212%20607%20162T602%2080V71Q602%2053%20603%2043T614%2025T640%2016Q668%2016%20686%2038T712%2085Q717%2099%20720%20102T735%20105Q755%20105%20755%2093Q755%2075%20731%2036Q693%20-21%20641%20-21H632Q571%20-21%20531%204T487%2082Q487%20109%20502%20166T517%20239Q517%20290%20474%20313Q459%20320%20449%20321T378%20323H309L277%20193Q244%2061%20244%2059Q244%2055%20245%2054T252%2050T269%2048T302%2046H333Q339%2038%20339%2037T336%2019Q332%206%20326%200H311Q275%202%20180%202Q146%202%20117%202T71%202T50%201Q33%201%2033%2010Q33%2012%2036%2024Q41%2043%2046%2045Q50%2046%2061%2046H67Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628Q287%20635%20230%20637ZM630%20554Q630%20586%20609%20608T523%20636Q521%20636%20500%20636T462%20637H440Q393%20637%20386%20627Q385%20624%20352%20494T319%20361Q319%20360%20388%20360Q466%20361%20492%20367Q556%20377%20592%20426Q608%20449%20619%20486T630%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2212%22%20d%3D%22M84%20237T84%20250T98%20270H679Q694%20262%20694%20250T679%20230H98Q84%20237%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6C%22%20d%3D%22M42%2046H56Q95%2046%20103%2060V68Q103%2077%20103%2091T103%20124T104%20167T104%20217T104%20272T104%20329Q104%20366%20104%20407T104%20482T104%20542T103%20586T103%20603Q100%20622%2089%20628T44%20637H26V660Q26%20683%2028%20683L38%20684Q48%20685%2067%20686T104%20688Q121%20689%20141%20690T171%20693T182%20694H185V379Q185%2062%20186%2060Q190%2052%20198%2049Q219%2046%20247%2046H263V0H255L232%201Q209%202%20183%202T145%203T107%203T57%201L34%200H26V46H42Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6F%22%20d%3D%22M28%20214Q28%20309%2093%20378T250%20448Q340%20448%20405%20380T471%20215Q471%20120%20407%2055T250%20-10Q153%20-10%2091%2057T28%20214ZM250%2030Q372%2030%20372%20193V225V250Q372%20272%20371%20288T364%20326T348%20362T317%20390T268%20410Q263%20411%20252%20411Q222%20411%20195%20399Q152%20377%20139%20338T126%20246V226Q126%20130%20145%2091Q177%2030%20250%2030Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-67%22%20d%3D%22M329%20409Q373%20453%20429%20453Q459%20453%20472%20434T485%20396Q485%20382%20476%20371T449%20360Q416%20360%20412%20390Q410%20404%20415%20411Q415%20412%20416%20414V415Q388%20412%20363%20393Q355%20388%20355%20386Q355%20385%20359%20381T368%20369T379%20351T388%20325T392%20292Q392%20230%20343%20187T222%20143Q172%20143%20123%20171Q112%20153%20112%20133Q112%2098%20138%2081Q147%2075%20155%2075T227%2073Q311%2072%20335%2067Q396%2058%20431%2026Q470%20-13%20470%20-72Q470%20-139%20392%20-175Q332%20-206%20250%20-206Q167%20-206%20107%20-175Q29%20-140%2029%20-75Q29%20-39%2050%20-15T92%2018L103%2024Q67%2055%2067%20108Q67%20155%2096%20193Q52%20237%2052%20292Q52%20355%20102%20398T223%20442Q274%20442%20318%20416L329%20409ZM299%20343Q294%20371%20273%20387T221%20404Q192%20404%20171%20388T145%20343Q142%20326%20142%20292Q142%20248%20149%20227T179%20192Q196%20182%20222%20182Q244%20182%20260%20189T283%20207T294%20227T299%20242Q302%20258%20302%20292T299%20343ZM403%20-75Q403%20-50%20389%20-34T348%20-11T299%20-2T245%200H218Q151%200%20138%20-6Q118%20-15%20107%20-34T95%20-74Q95%20-84%20101%20-97T122%20-127T170%20-155T250%20-167Q319%20-167%20361%20-139T403%20-75Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-50%22%20d%3D%22M287%20628Q287%20635%20230%20637Q206%20637%20199%20638T192%20648Q192%20649%20194%20659Q200%20679%20203%20681T397%20683Q587%20682%20600%20680Q664%20669%20707%20631T751%20530Q751%20453%20685%20389Q616%20321%20507%20303Q500%20302%20402%20301H307L277%20182Q247%2066%20247%2059Q247%2055%20248%2054T255%2050T272%2048T305%2046H336Q342%2037%20342%2035Q342%2019%20335%205Q330%200%20319%200Q316%200%20282%201T182%202Q120%202%2087%202T51%201Q33%201%2033%2011Q33%2013%2036%2025Q40%2041%2044%2043T67%2046Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628ZM645%20554Q645%20567%20643%20575T634%20597T609%20619T560%20635Q553%20636%20480%20637Q463%20637%20445%20637T416%20636T404%20636Q391%20635%20386%20627Q384%20621%20367%20550T332%20412T314%20344Q314%20342%20395%20342H407H430Q542%20342%20590%20392Q617%20419%20631%20471T645%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-7C%22%20d%3D%22M139%20-249H137Q125%20-249%20119%20-235V251L120%20737Q130%20750%20139%20750Q152%20750%20159%20735V-235Q151%20-249%20141%20-249H139Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-7A%22%20d%3D%22M347%20338Q337%20338%20294%20349T231%20360Q211%20360%20197%20356T174%20346T162%20335T155%20324L153%20320Q150%20317%20138%20317Q117%20317%20117%20325Q117%20330%20120%20339Q133%20378%20163%20406T229%20440Q241%20442%20246%20442Q271%20442%20291%20425T329%20392T367%20375Q389%20375%20411%20408T434%20441Q435%20442%20449%20442H462Q468%20436%20468%20434Q468%20430%20463%20420T449%20399T432%20377T418%20358L411%20349Q368%20298%20275%20214T160%20106L148%2094L163%2093Q185%2093%20227%2082T290%2071Q328%2071%20360%2090T402%20140Q406%20149%20409%20151T424%20153Q443%20153%20443%20143Q443%20138%20442%20134Q425%2072%20376%2031T278%20-11Q252%20-11%20232%206T193%2040T155%2057Q111%2057%2076%20-3Q70%20-11%2059%20-11H54H41Q35%20-5%2035%20-2Q35%2013%2093%2084Q132%20129%20225%20214T340%20322Q352%20338%20347%20338Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJCAL-4C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22968%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2024%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(11%2C-1102)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%22572%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%221240%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(3635%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%22700%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(0%2C-1149)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%22485%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(815%2C0)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4E%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22989%22%20y%3D%22-260%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%222673%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%223062%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223635%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%226648%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7593%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6C%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6F%22%20x%3D%22278%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-67%22%20x%3D%22779%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%228872%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%229262%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2210013%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%2210403%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%2210888%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(11167%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-7A%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%22658%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2212137%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2212527%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cmathcal%7BL%7D%3D%5Csum%7Bu%5Cin%20V%7D%5Csum_%7Bv%5Cin%20N_R%28u%29%7D-%5Clog%20%28P%28v%7Cz_u%29%29&id=oc9jJ)之后，如何优化（极小化）呢？
梯度下降：极小化03 Node Embeddings - 图83的一种简单方法。

  • 为所有03 Node Embeddings - 图84初始化一个随机值03 Node Embeddings - 图85。
  • 迭代至聚合：
    • 所有03 Node Embeddings - 图86，计算导数03 Node Embeddings - 图87；
    • 所有03 Node Embeddings - 图88，向导数的方向迈进一步：03 Node Embeddings - 图89, 03 Node Embeddings - 图90为学习率。

随机梯度下降：不是在所有的例子中评估梯度，而是在每个训练例子中评估梯度。

  • 为所有03 Node Embeddings - 图91初始化一个随机值03 Node Embeddings - 图92。
  • 迭代至聚合：03 Node Embeddings - 图93
    • 抽样一个节点03 Node Embeddings - 图94，对所有03 Node Embeddings - 图95计算导数03 Node Embeddings - 图96；
    • 所有03 Node Embeddings - 图97，更新：03 Node Embeddings - 图98, 03 Node Embeddings - 图99为学习率。

      Summary

  1. 从图上的每个节点开始运行短的固定长度的随机游走；
  2. 对于每个节点03 Node Embeddings - 图100收集03 Node Embeddings - 图101，从03 Node Embeddings - 图102开始随机游走访问多个节点集；
  3. 使用随机梯度下降法优化嵌入：03 Node Embeddings - 图103%7D-%5Clog%20(P(v%7Czu))%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJCAL-4C%22%20d%3D%22M62%20-22T47%20-22T32%20-11Q32%20-1%2056%2024T83%2055Q113%2096%20138%20172T180%20320T234%20473T323%20609Q364%20649%20419%20677T531%20705Q559%20705%20578%20696T604%20671T615%20645T618%20623V611Q618%20582%20615%20571T598%20548Q581%20531%20558%20520T518%20509Q503%20509%20503%20520Q503%20523%20505%20536T507%20560Q507%20590%20494%20610T452%20630Q423%20630%20410%20617Q367%20578%20333%20492T271%20301T233%20170Q211%20123%20204%20112L198%20103L224%20102Q281%20102%20369%2079T509%2052H523Q535%2064%20544%2087T579%20128Q616%20152%20641%20152Q656%20152%20656%20142Q656%20101%20588%2040T433%20-22Q381%20-22%20289%201T156%2028L141%2029L131%2020Q111%200%2087%20-11Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ2-2211%22%20d%3D%22M60%20948Q63%20950%20665%20950H1267L1325%20815Q1384%20677%201388%20669H1348L1341%20683Q1320%20724%201285%20761Q1235%20809%201174%20838T1033%20881T882%20898T699%20902H574H543H251L259%20891Q722%20258%20724%20252Q725%20250%20724%20246Q721%20243%20460%20-56L196%20-356Q196%20-357%20407%20-357Q459%20-357%20548%20-357T676%20-358Q812%20-358%20896%20-353T1063%20-332T1204%20-283T1307%20-196Q1328%20-170%201348%20-124H1388Q1388%20-125%201381%20-145T1356%20-210T1325%20-294L1267%20-449L666%20-450Q64%20-450%2061%20-448Q55%20-446%2055%20-439Q55%20-437%2057%20-433L590%20177Q590%20178%20557%20222T452%20366T322%20544L56%20909L55%20924Q55%20945%2060%20948Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-75%22%20d%3D%22M21%20287Q21%20295%2030%20318T55%20370T99%20420T158%20442Q204%20442%20227%20417T250%20358Q250%20340%20216%20246T182%20105Q182%2062%20196%2045T238%2027T291%2044T328%2078L339%2095Q341%2099%20377%20247Q407%20367%20413%20387T427%20416Q444%20431%20463%20431Q480%20431%20488%20421T496%20402L420%2084Q419%2079%20419%2068Q419%2043%20426%2035T447%2026Q469%2029%20482%2057T512%20145Q514%20153%20532%20153Q551%20153%20551%20144Q550%20139%20549%20130T540%2098T523%2055T498%2017T462%20-8Q454%20-10%20438%20-10Q372%20-10%20347%2046Q345%2045%20336%2036T318%2021T296%206T267%20-6T233%20-11Q189%20-11%20155%207Q103%2038%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2208%22%20d%3D%22M84%20250Q84%20372%20166%20450T360%20539Q361%20539%20377%20539T419%20540T469%20540H568Q583%20532%20583%20520Q583%20511%20570%20501L466%20500Q355%20499%20329%20494Q280%20482%20242%20458T183%20409T147%20354T129%20306T124%20272V270H568Q583%20262%20583%20250T568%20230H124V228Q124%20207%20134%20177T167%20112T231%2048T328%207Q355%201%20466%200H570Q583%20-10%20583%20-20Q583%20-32%20568%20-40H471Q464%20-40%20446%20-40T417%20-41Q262%20-41%20172%2045Q84%20127%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-56%22%20d%3D%22M52%20648Q52%20670%2065%20683H76Q118%20680%20181%20680Q299%20680%20320%20683H330Q336%20677%20336%20674T334%20656Q329%20641%20325%20637H304Q282%20635%20274%20635Q245%20630%20242%20620Q242%20618%20271%20369T301%20118L374%20235Q447%20352%20520%20471T595%20594Q599%20601%20599%20609Q599%20633%20555%20637Q537%20637%20537%20648Q537%20649%20539%20661Q542%20675%20545%20679T558%20683Q560%20683%20570%20683T604%20682T668%20681Q737%20681%20755%20683H762Q769%20676%20769%20672Q769%20655%20760%20640Q757%20637%20743%20637Q730%20636%20719%20635T698%20630T682%20623T670%20615T660%20608T652%20599T645%20592L452%20282Q272%20-9%20266%20-16Q263%20-18%20259%20-21L241%20-22H234Q216%20-22%20216%20-15Q213%20-9%20177%20305Q139%20623%20138%20626Q133%20637%2076%20637H59Q52%20642%2052%20648Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-76%22%20d%3D%22M173%20380Q173%20405%20154%20405Q130%20405%20104%20376T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Q21%20294%2029%20316T53%20368T97%20419T160%20441Q202%20441%20225%20417T249%20361Q249%20344%20246%20335Q246%20329%20231%20291T200%20202T182%20113Q182%2086%20187%2069Q200%2026%20250%2026Q287%2026%20319%2060T369%20139T398%20222T409%20277Q409%20300%20401%20317T383%20343T365%20361T357%20383Q357%20405%20376%20424T417%20443Q436%20443%20451%20425T467%20367Q467%20340%20455%20284T418%20159T347%2040T241%20-11Q177%20-11%20139%2022Q102%2054%20102%20117Q102%20148%20110%20181T151%20298Q173%20362%20173%20380Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-4E%22%20d%3D%22M234%20637Q231%20637%20226%20637Q201%20637%20196%20638T191%20649Q191%20676%20202%20682Q204%20683%20299%20683Q376%20683%20387%20683T401%20677Q612%20181%20616%20168L670%20381Q723%20592%20723%20606Q723%20633%20659%20637Q635%20637%20635%20648Q635%20650%20637%20660Q641%20676%20643%20679T653%20683Q656%20683%20684%20682T767%20680Q817%20680%20843%20681T873%20682Q888%20682%20888%20672Q888%20650%20880%20642Q878%20637%20858%20637Q787%20633%20769%20597L620%207Q618%200%20599%200Q585%200%20582%202Q579%205%20453%20305L326%20604L261%20344Q196%2088%20196%2079Q201%2046%20268%2046H278Q284%2041%20284%2038T282%2019Q278%206%20272%200H259Q228%202%20151%202Q123%202%20100%202T63%202T46%201Q31%201%2031%2010Q31%2014%2034%2026T39%2040Q41%2046%2062%2046Q130%2049%20150%2085Q154%2091%20221%20362L289%20634Q287%20635%20234%20637Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-52%22%20d%3D%22M230%20637Q203%20637%20198%20638T193%20649Q193%20676%20204%20682Q206%20683%20378%20683Q550%20682%20564%20680Q620%20672%20658%20652T712%20606T733%20563T739%20529Q739%20484%20710%20445T643%20385T576%20351T538%20338L545%20333Q612%20295%20612%20223Q612%20212%20607%20162T602%2080V71Q602%2053%20603%2043T614%2025T640%2016Q668%2016%20686%2038T712%2085Q717%2099%20720%20102T735%20105Q755%20105%20755%2093Q755%2075%20731%2036Q693%20-21%20641%20-21H632Q571%20-21%20531%204T487%2082Q487%20109%20502%20166T517%20239Q517%20290%20474%20313Q459%20320%20449%20321T378%20323H309L277%20193Q244%2061%20244%2059Q244%2055%20245%2054T252%2050T269%2048T302%2046H333Q339%2038%20339%2037T336%2019Q332%206%20326%200H311Q275%202%20180%202Q146%202%20117%202T71%202T50%201Q33%201%2033%2010Q33%2012%2036%2024Q41%2043%2046%2045Q50%2046%2061%2046H67Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628Q287%20635%20230%20637ZM630%20554Q630%20586%20609%20608T523%20636Q521%20636%20500%20636T462%20637H440Q393%20637%20386%20627Q385%20624%20352%20494T319%20361Q319%20360%20388%20360Q466%20361%20492%20367Q556%20377%20592%20426Q608%20449%20619%20486T630%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2212%22%20d%3D%22M84%20237T84%20250T98%20270H679Q694%20262%20694%20250T679%20230H98Q84%20237%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6C%22%20d%3D%22M42%2046H56Q95%2046%20103%2060V68Q103%2077%20103%2091T103%20124T104%20167T104%20217T104%20272T104%20329Q104%20366%20104%20407T104%20482T104%20542T103%20586T103%20603Q100%20622%2089%20628T44%20637H26V660Q26%20683%2028%20683L38%20684Q48%20685%2067%20686T104%20688Q121%20689%20141%20690T171%20693T182%20694H185V379Q185%2062%20186%2060Q190%2052%20198%2049Q219%2046%20247%2046H263V0H255L232%201Q209%202%20183%202T145%203T107%203T57%201L34%200H26V46H42Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6F%22%20d%3D%22M28%20214Q28%20309%2093%20378T250%20448Q340%20448%20405%20380T471%20215Q471%20120%20407%2055T250%20-10Q153%20-10%2091%2057T28%20214ZM250%2030Q372%2030%20372%20193V225V250Q372%20272%20371%20288T364%20326T348%20362T317%20390T268%20410Q263%20411%20252%20411Q222%20411%20195%20399Q152%20377%20139%20338T126%20246V226Q126%20130%20145%2091Q177%2030%20250%2030Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-67%22%20d%3D%22M329%20409Q373%20453%20429%20453Q459%20453%20472%20434T485%20396Q485%20382%20476%20371T449%20360Q416%20360%20412%20390Q410%20404%20415%20411Q415%20412%20416%20414V415Q388%20412%20363%20393Q355%20388%20355%20386Q355%20385%20359%20381T368%20369T379%20351T388%20325T392%20292Q392%20230%20343%20187T222%20143Q172%20143%20123%20171Q112%20153%20112%20133Q112%2098%20138%2081Q147%2075%20155%2075T227%2073Q311%2072%20335%2067Q396%2058%20431%2026Q470%20-13%20470%20-72Q470%20-139%20392%20-175Q332%20-206%20250%20-206Q167%20-206%20107%20-175Q29%20-140%2029%20-75Q29%20-39%2050%20-15T92%2018L103%2024Q67%2055%2067%20108Q67%20155%2096%20193Q52%20237%2052%20292Q52%20355%20102%20398T223%20442Q274%20442%20318%20416L329%20409ZM299%20343Q294%20371%20273%20387T221%20404Q192%20404%20171%20388T145%20343Q142%20326%20142%20292Q142%20248%20149%20227T179%20192Q196%20182%20222%20182Q244%20182%20260%20189T283%20207T294%20227T299%20242Q302%20258%20302%20292T299%20343ZM403%20-75Q403%20-50%20389%20-34T348%20-11T299%20-2T245%200H218Q151%200%20138%20-6Q118%20-15%20107%20-34T95%20-74Q95%20-84%20101%20-97T122%20-127T170%20-155T250%20-167Q319%20-167%20361%20-139T403%20-75Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-50%22%20d%3D%22M287%20628Q287%20635%20230%20637Q206%20637%20199%20638T192%20648Q192%20649%20194%20659Q200%20679%20203%20681T397%20683Q587%20682%20600%20680Q664%20669%20707%20631T751%20530Q751%20453%20685%20389Q616%20321%20507%20303Q500%20302%20402%20301H307L277%20182Q247%2066%20247%2059Q247%2055%20248%2054T255%2050T272%2048T305%2046H336Q342%2037%20342%2035Q342%2019%20335%205Q330%200%20319%200Q316%200%20282%201T182%202Q120%202%2087%202T51%201Q33%201%2033%2011Q33%2013%2036%2025Q40%2041%2044%2043T67%2046Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628ZM645%20554Q645%20567%20643%20575T634%20597T609%20619T560%20635Q553%20636%20480%20637Q463%20637%20445%20637T416%20636T404%20636Q391%20635%20386%20627Q384%20621%20367%20550T332%20412T314%20344Q314%20342%20395%20342H407H430Q542%20342%20590%20392Q617%20419%20631%20471T645%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-7C%22%20d%3D%22M139%20-249H137Q125%20-249%20119%20-235V251L120%20737Q130%20750%20139%20750Q152%20750%20159%20735V-235Q151%20-249%20141%20-249H139Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-7A%22%20d%3D%22M347%20338Q337%20338%20294%20349T231%20360Q211%20360%20197%20356T174%20346T162%20335T155%20324L153%20320Q150%20317%20138%20317Q117%20317%20117%20325Q117%20330%20120%20339Q133%20378%20163%20406T229%20440Q241%20442%20246%20442Q271%20442%20291%20425T329%20392T367%20375Q389%20375%20411%20408T434%20441Q435%20442%20449%20442H462Q468%20436%20468%20434Q468%20430%20463%20420T449%20399T432%20377T418%20358L411%20349Q368%20298%20275%20214T160%20106L148%2094L163%2093Q185%2093%20227%2082T290%2071Q328%2071%20360%2090T402%20140Q406%20149%20409%20151T424%20153Q443%20153%20443%20143Q443%20138%20442%20134Q425%2072%20376%2031T278%20-11Q252%20-11%20232%206T193%2040T155%2057Q111%2057%2076%20-3Q70%20-11%2059%20-11H54H41Q35%20-5%2035%20-2Q35%2013%2093%2084Q132%20129%20225%20214T340%20322Q352%20338%20347%20338Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJCAL-4C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22968%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2024%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(11%2C-1102)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%22572%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-56%22%20x%3D%221240%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3Cg%20transform%3D%22translate(3635%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-2211%22%20x%3D%22700%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(0%2C-1149)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2208%22%20x%3D%22485%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(815%2C0)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-4E%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.574)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-52%22%20x%3D%22989%22%20y%3D%22-260%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%222673%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%223062%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%223635%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%226648%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(7593%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6C%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6F%22%20x%3D%22278%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-67%22%20x%3D%22779%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%228872%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%229262%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2210013%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-76%22%20x%3D%2210403%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%2210888%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(11167%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-7A%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%22658%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2212137%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2212527%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cmathcal%7BL%7D%3D%5Csum%7Bu%5Cin%20V%7D%5Csum_%7Bv%5Cin%20N_R%28u%29%7D-%5Clog%20%28P%28v%7Cz_u%29%29&id=yhed8)，我们可以使用负抽样来有效地近似。

    node2vec

    到目前为止，我们已经描述了在给定随机游走策略03 Node Embeddings - 图104的情况下如何优化嵌入，我们应该用什么策略来进行这些随机游走？最简单的想法：从每个节点开始运行固定长度的无偏随机游走（如DeepWalk from Perozzi et al., 2013），问题是相似的概念太受限制了。那我们如何广义化这个呢？
    Overview of node2vec (ref: Grover et al. 2016. node2vec: Scalable Feature Learning for Networks. KDD.)：
  • 目标：在特征空间内嵌入具有相似网络邻域的节点。
  • 我们将此目标定义为一个最大似然优化问题，独立于下游预测任务。
  • 关键观察：节点03 Node Embeddings - 图105的网络邻域03 Node Embeddings - 图106的灵活概念导致了丰富的节点嵌入。
  • 开发偏二阶随机游走03 Node Embeddings - 图107生成节点03 Node Embeddings - 图108的网络邻域03 Node Embeddings - 图109。

node2vec：Biased Walks
想法：使用灵活的、有偏的随机游走，可以在网络的局部和全局视野之间进行权衡(Grover and Leskovec, 2016)。
定义给定节点03 Node Embeddings - 图110的邻域03 Node Embeddings - 图111的两种经典策略：
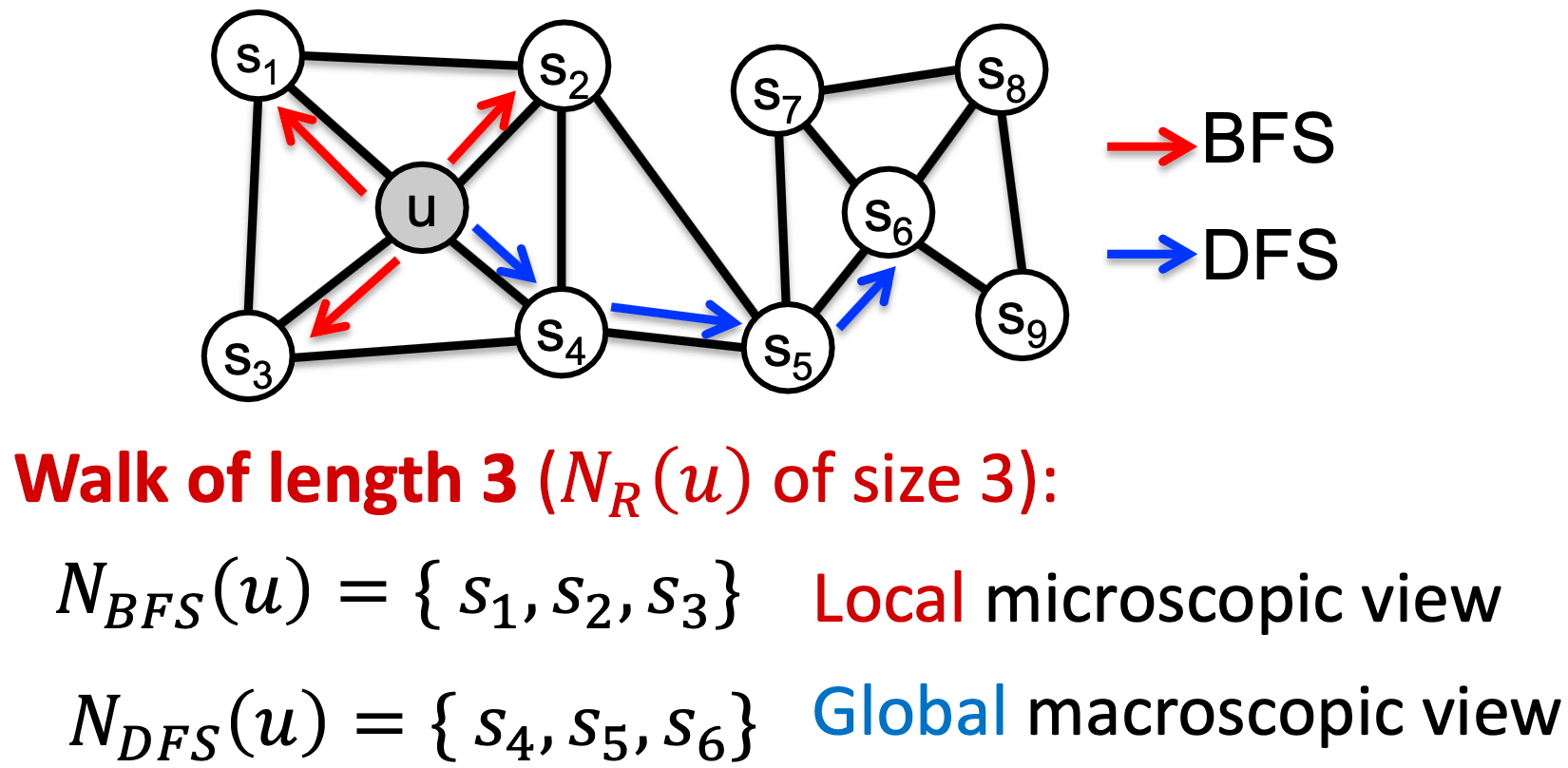
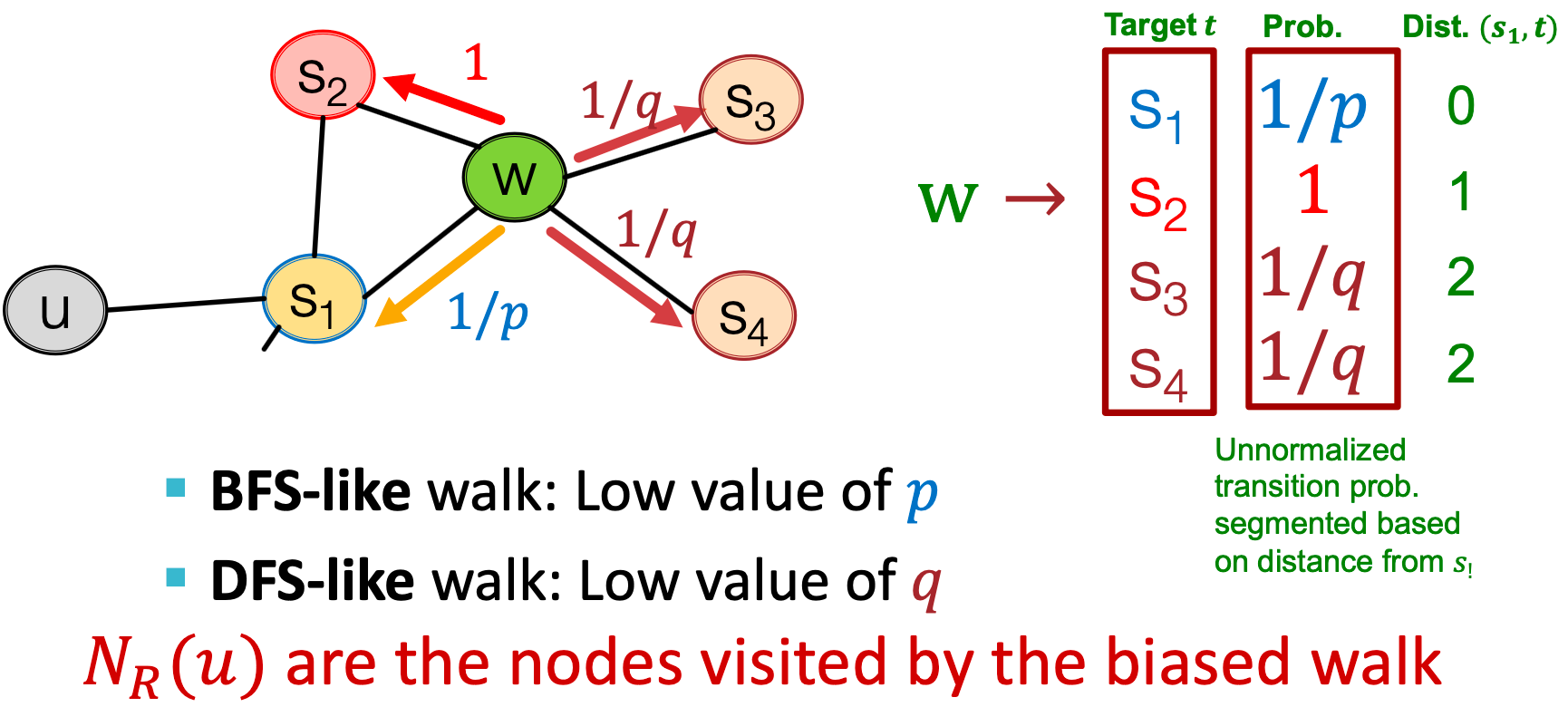
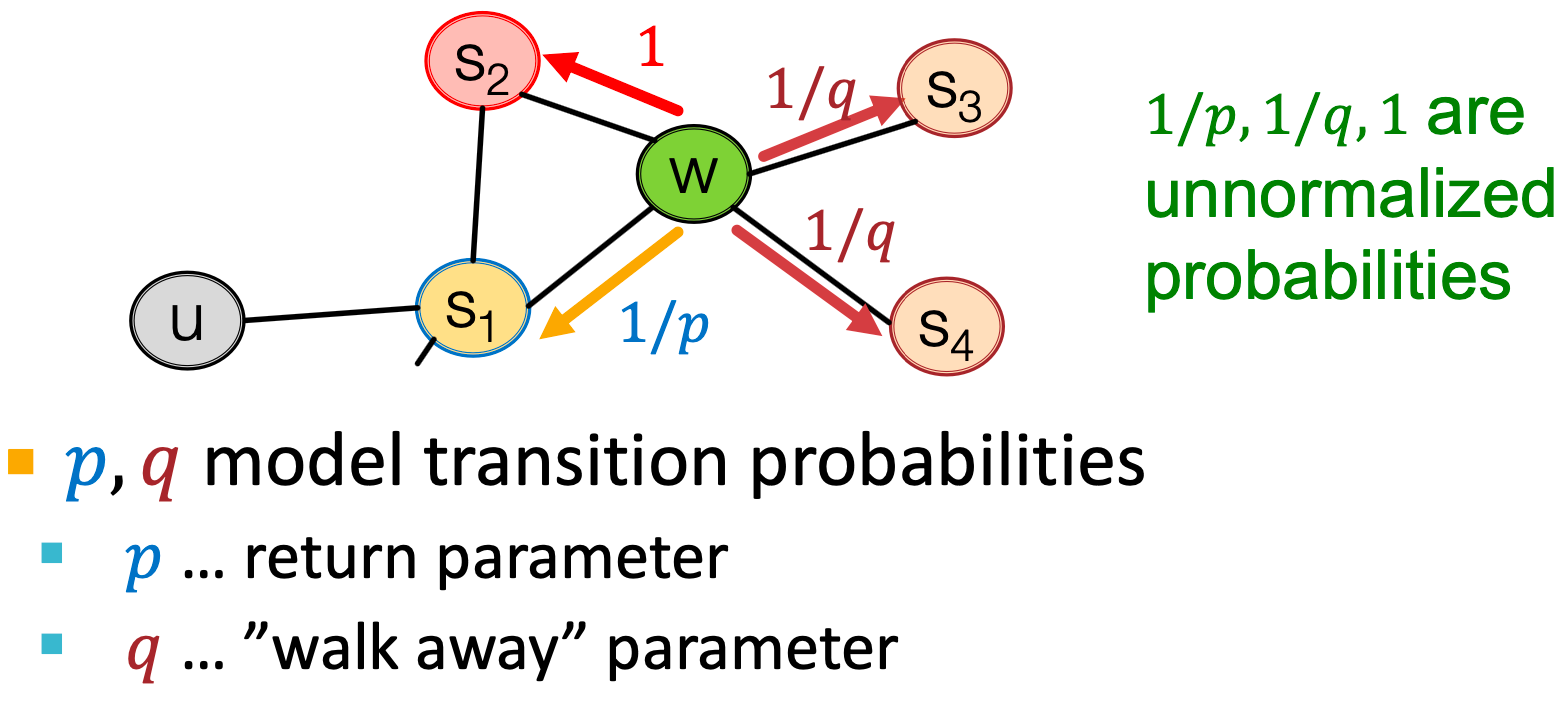
image.png
image.pngimage.png
给定节点03 Node Embeddings - 图115生成邻域03 Node Embeddings - 图116的有偏定长随机游走03 Node Embeddings - 图117，有两个参数：

  • 返回参数03 Node Embeddings - 图118：返回到前一个节点；
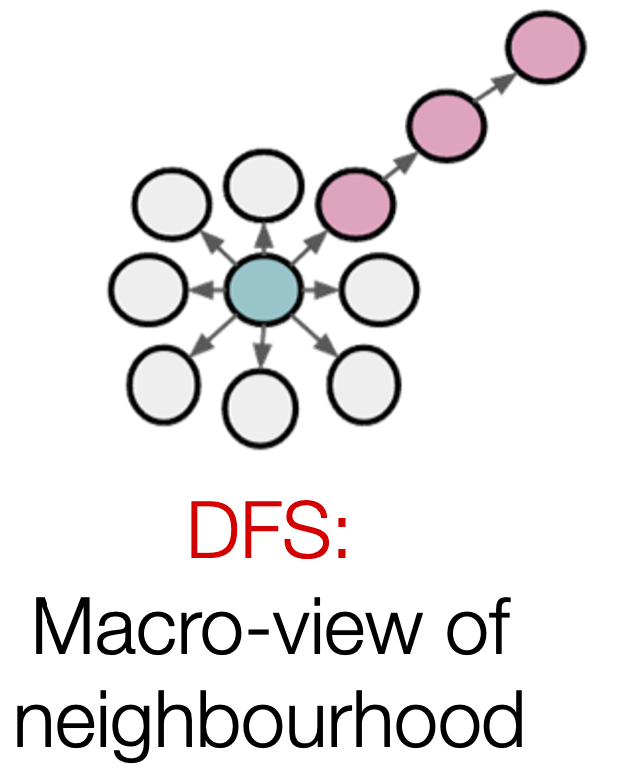
  • 输入输出参数03 Node Embeddings - 图119：向外(DFS) vs.向内(BFS)；直观地说，03 Node Embeddings - 图120是BFS vs. DFS的“比率”。

随机游走只是遍历边03 Node Embeddings - 图121，现在是03 Node Embeddings - 图122
image.pngimage.png
node2vec算法：

  1. 计算随机游走概率；
  2. 从每个节点03 Node Embeddings - 图125开始，模拟长度03 Node Embeddings - 图126的03 Node Embeddings - 图127个随机游走；
  3. 利用随机梯度下降法优化node2vec目标。

时间复杂度是线性的，所有3个步骤都可以单独并行。
其他随机游走ideas：

  • 不同类型的有偏随机游走：
  • 可替换优化框架：

  • 网络预处理技术：

  • 核心思想：嵌入节点，使嵌入空间的距离反映原网络中节点的相似性。

  • 节点相似度的不同概念：
    • Naïve：如果两个节点连接，则相似；
    • 邻域重叠(在第2讲中已涉及)；
    • 随机漫步方法(今天讨论)。

那我们应该使用什么方法呢？没有一种方法在所有情况下都是成功的….
例如，node2vec在节点分类上表现得更好，而替代方法在链接预测上表现得更好(Goyal and Ferrara, 2017 survey)。随机游走方法通常更有效。一般来说，必须选择与应用相匹配的节点相似度定义。

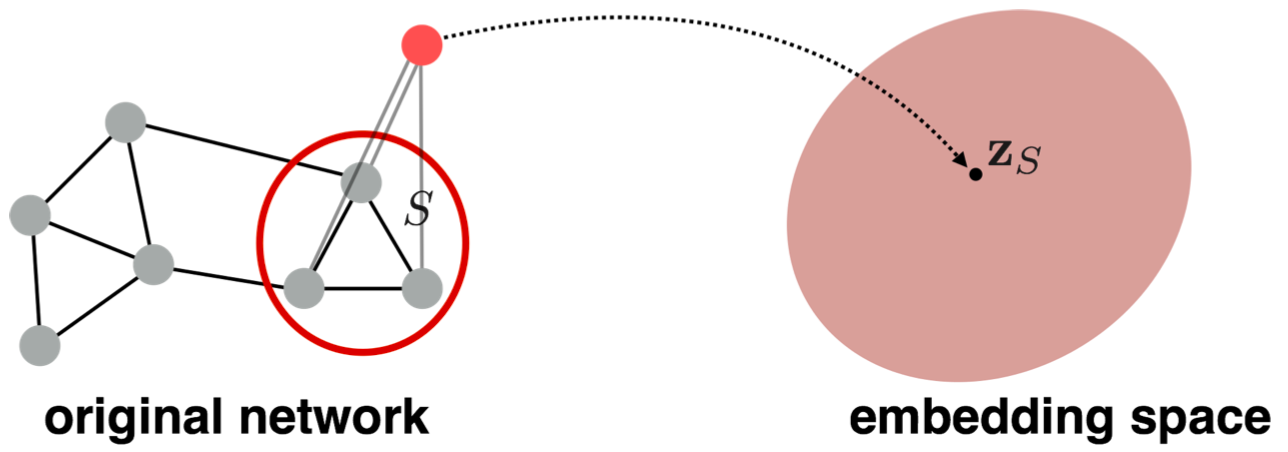
Embedding Entire Graphs

目标：希望嵌入一个子图或整个图03 Node Embeddings - 图128。图嵌入：03 Node Embeddings - 图129。
任务：

  • 对有毒分子和无毒分子进行分类；
  • 识别异常图。

image.png

Approach 1

  • 在(子)图03 Node Embeddings - 图131上运行标准的图嵌入技术
  • 然后对(子)图03 Node Embeddings - 图132中的节点嵌入求和(或平均)，03 Node Embeddings - 图133

  • Duvenaud et al., 2016 根据分子的图结构对分子进行分类

    Approach 2

    引入一个“虚拟节点”来表示(子)图，并运行标准的图嵌入技术。
    image.png
    Li et al., 2016 提出作为一种通用的子图嵌入技术。

    Approach 3: Anonymous Walk Embeddings

    anonymous walk中的状态对应于我们在随机游走中第一次访问该节点的索引。
    image.png
    Anonymous Walk Embeddings, ICML 2018 https://arxiv.org/pdf/1805.11921.pdf
    访问节点的身份不可知(因此是匿名的)
    如RW1：
    image.png
    image.png
    匿名游走的数量呈指数增长，有5个anon. walks 03 Node Embeddings - 图138的长度为3，分别是03 Node Embeddings - 图139
    匿名游走的简单使用

  • 模拟匿名游走03 Node Embeddings - 图140的03 Node Embeddings - 图141步骤，并记录它们的计数；

  • 把这个图表示成这些游走的概率分布；
  • 例子：设03 Node Embeddings - 图142，然后我们可以把这个图表示成一个5维的向量，因为有5个长度为3的匿名游走03 Node Embeddings - 图143，分别是111、112、121、122、123。03 Node Embeddings - 图144表示图03 Node Embeddings - 图145中匿名游走03 Node Embeddings - 图146的概率。

    抽样匿名游走

    生成独立的03 Node Embeddings - 图147个随机游走集合，把这个图表示成这些游走的概率分布，我们需要的03 Node Embeddings - 图148个随机游走是多少呢？
    我们希望分布误差大于03 Node Embeddings - 图149、概率小于03 Node Embeddings - 图150，03 Node Embeddings - 图151, 其中03 Node Embeddings - 图152表示长度为03 Node Embeddings - 图153的匿名游走的总数量。如，长度为03 Node Embeddings - 图154的匿名游走共有03 Node Embeddings - 图155个，若设03 Node Embeddings - 图156且03 Node Embeddings - 图157，则我们需要生成03 Node Embeddings - 图158个随机游走。

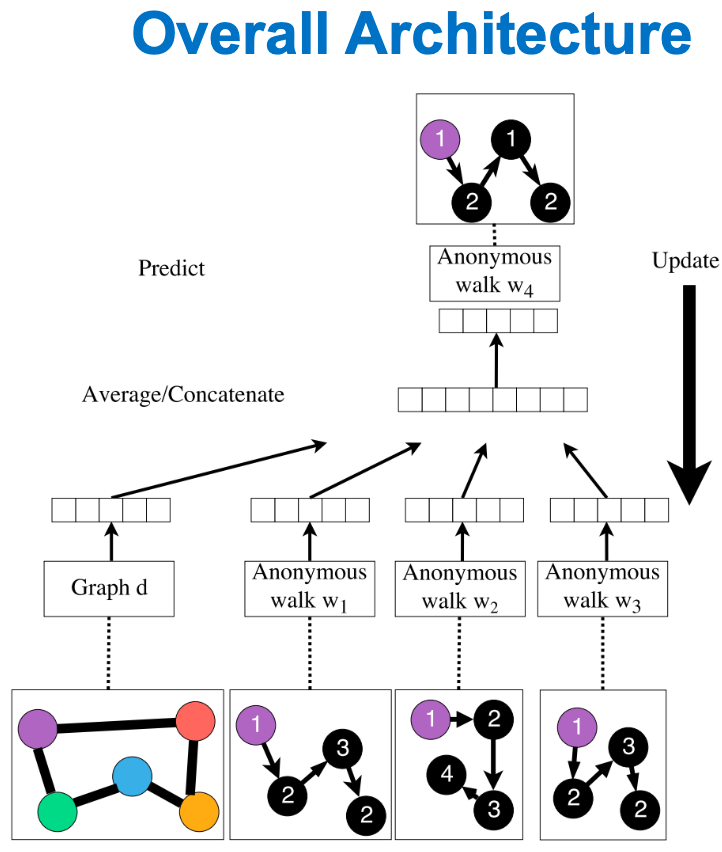
    New idea: Learn Walk Embeddings

    我们不是简单地用每次游走发生的次数来表示它，而是学习嵌入03 Node Embeddings - 图159的匿名行走03 Node Embeddings - 图160。
    学习一个图嵌入03 Node Embeddings - 图161和所有匿名游走嵌入03 Node Embeddings - 图162。:𝑖= 1…𝜂}，其中03 Node Embeddings - 图163是采样匿名游走的数量。
    如何嵌入游走？想法是嵌入游走，使得满足下一个游走可以被预测。

一个向量参数03 Node Embeddings - 图164为输入图，要学习的整个图的嵌入。从节点1开始，抽样匿名随机游走，例如：
image.pngimage.png
学习预测在03 Node Embeddings - 图167窗口同时发生的游走，如给定03 Node Embeddings - 图168预测03 Node Embeddings - 图169，若03 Node Embeddings - 图170.
目标函数：03 Node Embeddings - 图171，对图中所有节点的目标求和。

  • 运行03 Node Embeddings - 图172个不同的长度03 Node Embeddings - 图173的随机游走03 Node Embeddings - 图174，03 Node Embeddings - 图175
  • 学习预测在03 Node Embeddings - 图176窗口同时发生的游走
  • 估计匿名游走03 Node Embeddings - 图177的嵌入03 Node Embeddings - 图178

设03 Node Embeddings - 图179为所有可能的游走嵌入数量，目标函数03 Node Embeddings - 图180
03 Node Embeddings - 图181（需要负采样）
03 Node Embeddings - 图182

  • 03 Node Embeddings - 图183表示窗口中匿名游走嵌入的平均值，与图嵌入03 Node Embeddings - 图184拼接
  • 03 Node Embeddings - 图185是学习参数，表示线性层
  • 经过优化，我们得到了图的嵌入03 Node Embeddings - 图186(可学习参数)。
  • 使用03 Node Embeddings - 图187做预测，如图分类
    • Option1：内积核03 Node Embeddings - 图188（Lecture2）
    • Option2：使用以03 Node Embeddings - 图189为输入进行分类的神经网络

image.png

Summary

我们讨论了图嵌入的3种思路：

  • Approach1：嵌入节点并求和/平均
  • Approach2：创建跨越(子)图的超级节点，然后嵌入该节点

  • Approach3：匿名游走嵌入，

    • idea1：对匿名游走进行采样，并将图表示为每个匿名游走发生次数的部分；
    • idea2：嵌入匿名游走，将它们的嵌入拼接起来，得到一个图的嵌入。

      Preview: Hierarchical Embeddings

      我们将在Lecture8中讨论更高级的获取图嵌入的方法。
      我们可以在图中分层聚类节点，并根据这些聚类对节点嵌入进行求和/平均。
      image.png

      How to Use Embeddings

      如何使用节点嵌入03 Node Embeddings - 图192：

  • 聚类/社区检测：聚类点03 Node Embeddings - 图193

  • 节点分类：基于03 Node Embeddings - 图194预测节点03 Node Embeddings - 图195的标签
  • 链接预测：基于03 Node Embeddings - 图196预测边03 Node Embeddings - 图197，我们可以concatenate、avg、product、或取嵌入之间的不同
    • Concatenate：03 Node Embeddings - 图198
    • Hadamard：03 Node Embeddings - 图199 (每个坐标轴上相乘)
    • Sum/Avg：03 Node Embeddings - 图200
    • Distance：03 Node Embeddings - 图201

  • 图分类：图嵌入03 Node Embeddings - 图202通过聚合节点嵌入或匿名随机游走，基于图嵌入03 Node Embeddings - 图203预测标签

    Summary

    我们讨论了图表示学习，这是一种学习节点和图嵌入下游任务的方法，不需要特征工程。

  • Encoder-decoder框架：

    • Encoder：嵌入查找
    • Decoder：基于嵌入预测评分，匹配节点相似度
  • 节点相似性度量：(有偏的)随机游走，如DeepWalk、Node2Vec
  • 对图嵌入的扩展：节点嵌入聚合和匿名游走嵌入