一、引言
二、图的性质
三、Erdos-Renyi随机图模型
- （1）随机图模型的性质
- （2）MSN与随机图的性质比较
四、The Small-World Model小世界模型
五、Kronecker Graph Model
参考链接

一、引言

1、Networks/Graphs的两种类型（有时区别比较模糊）

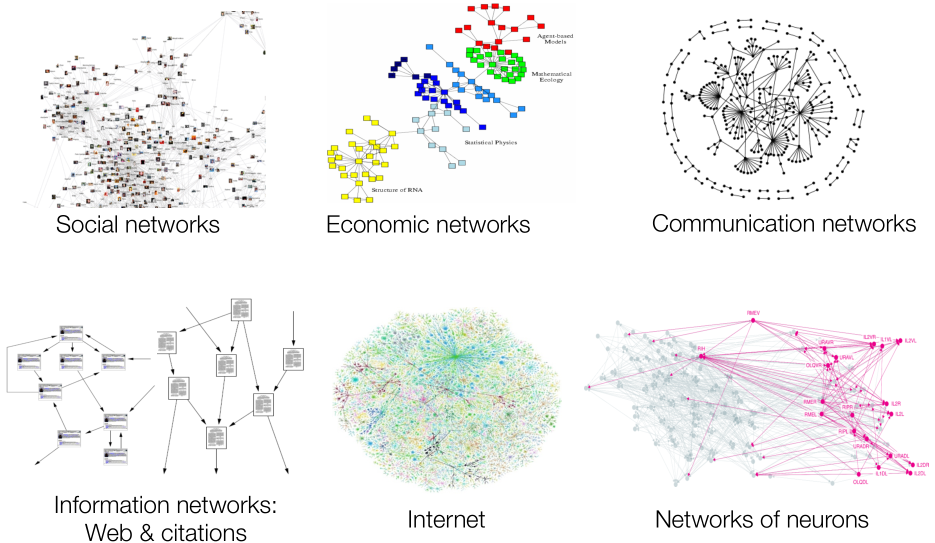
Networks（Natural Graphs）：社会是70多亿个人的集合，通信系统连接电子设备，基因/蛋白质之间的相互作用调节着生命，我们的思想隐藏在大脑中数十亿神经元之间的连接中。Network, node, link
Information Graphs：信息/知识的组织和联系，场景中物体之间关系的场景图，相似性网络。Graph. vertex, edge

微信截图_20210227181803.png

2、图网络的应用方法

节点分类：预测给定节点的类别，如在异常检测问题中区分正常用户与异常用户；
链接预测：预测两个节点是否相连，如在推荐网络中预测用户A是否会购买商品B，判断两个节点的社交关系(朋友，家人等)；
社区发现：识别紧密相连的节点群，如划分出一个网络中家庭成员、朋友、大学同学、高中同学的社交圈，可以理解为一种聚类方法；
网络相似：测量两个节点/网络的相似性，如通过学习到每个节点的低维向量表示后，衡量节点之间的相似度。

3、一个图的组成部分
nodes, vertices
links, edges
network, graph

4、图的类型及网络表示

（1）图的类型
无向图 undirected graph
有向图 directed graph
完全图 complete graph
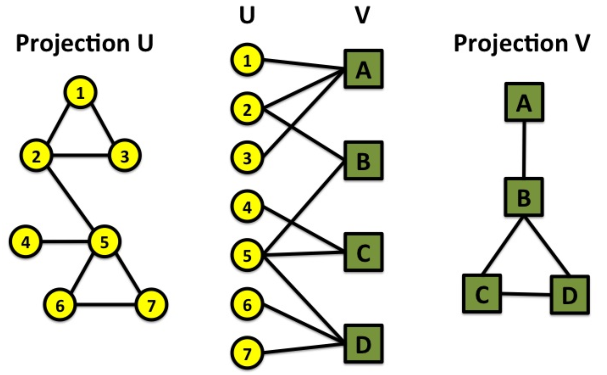
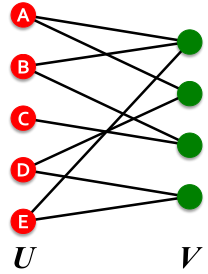
二分图 bipartite graph：二部图的节点可以分为两个不相交的集合U和V，从而每个链接都将U中的节点连接到V中的一个节点，即U和V是独立的集合（U、V的内部没有边）。如作者-论文、演员-电影等。
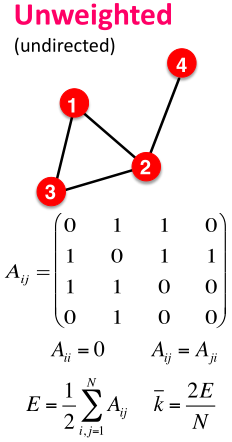
无权图 unweighted graph：图的节点之间没有权重
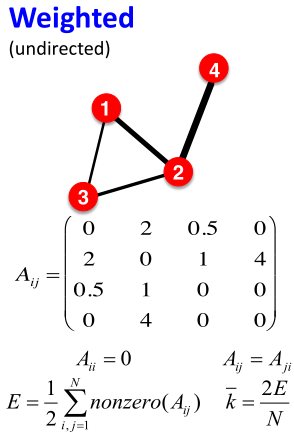
加权图 weighted graph：图的节点之间有权重
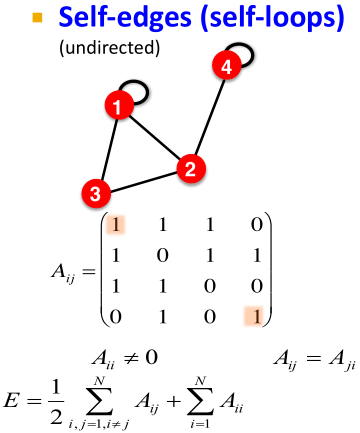
自环图 self-edges（self-loops）：有边指向节点自己
多重图 multigraph：两个节点之间有多个边

（2）网络表示
Email network: directed multigraph with self-edges
Facebook friendships: undirected, unweighted
Citation networks: unweighted, directed, acyclic 非周期的；非循环的；无环的；非环状的
Collaboration networks: undirected multigraph or weighted graph
Mobile phone calls: directed, (weighted?) multigraph
Protein Interactions 蛋白质相互作用: undirected, unweighted with self-interactions
5、图的相关定义
（1）图的表示
可用邻接矩阵Adjacency Matrix来表示图。若节点与节点相连，则；否则。

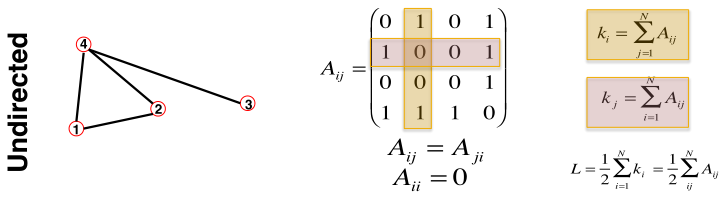
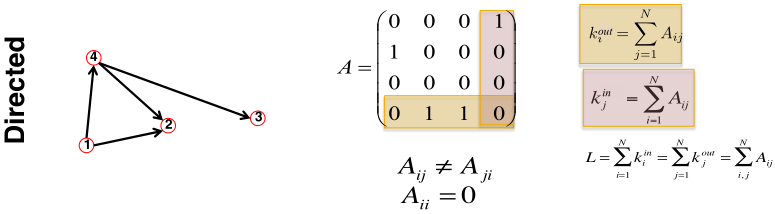
（2）度与边
1）无向图

节点度：与节点相邻的边数
平均度
2）有向图

in-degree：
out-degree：
一个节点总的度

3）完全图

N个节点上的无向图的最大边数是

一个边数为 01&02 图模型的基本介绍 - 图23 的无向图称为完全图，其平均度为 01&02 图模型的基本介绍 - 图24 。

4）二分图

folded/projected二分图：

5）无权图

6）加权图

7）自环图

8）多重图

（3）边的属性

可能的选择有：

权重 weight，如联系的频次
排序 ranking，如最好的朋友、第二好的朋友…
类型 type，如朋友、同事、亲戚
sign，如朋友vs敌人、信任vs不信任
属性取决于图的其余部分的结构：共同好友的数量

（4）图的连通性

1）无向图的连通性
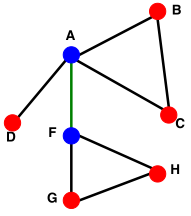如果擦除绿色的边（AF），则图不连接。
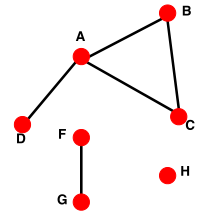节点H是孤立节点。一个不相连的图由两个或多个连接的节点组成。
例子：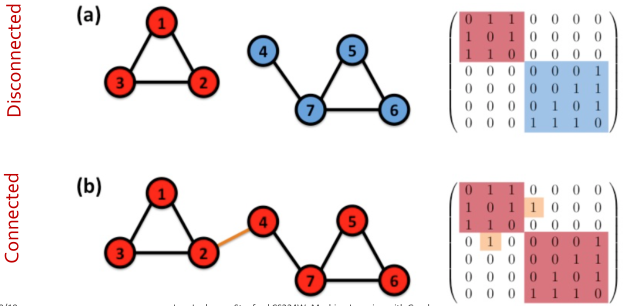

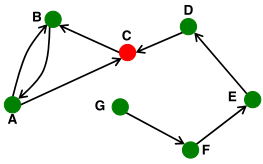
2）有向图的连通性
强连通有向图：具有从每个节点到每个其他节点的路径，反之亦然(例如，A-B路径和B-A路径)
弱连通有向图：如果不考虑边的方向的话，是连接的

如下图，该图是连接的，但不是强连接，如根据边的方向，F-G路径不通。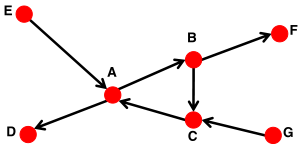

强连接组件(Strongly connected components，SCCs)可以被识别，但不是每个节点都是显要的强连接组件的一部分。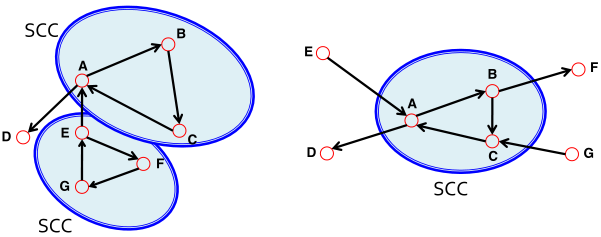

In-component : nodes that can reach the SCC,
Out-component : nodes that can be reached from the SCC.

二、图的性质

Key Network Properties：

度分布 degree distribution：
路径长度 path length：
聚类系数 clustering coefficient：
连通分支 connected components：
1、度分布
度分布：随机选择的节点的度为的概率。
设，则。

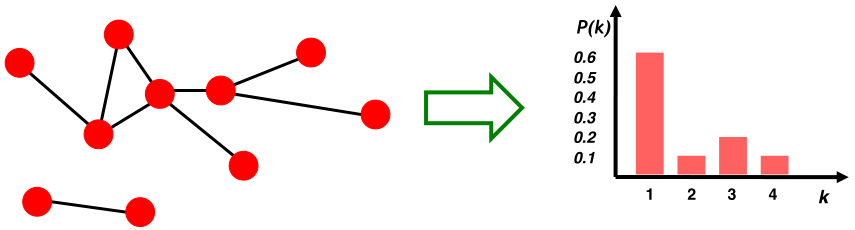
对有向图来说，有in-degree与out-degree分布。
2、路径
一条路径可以与自己相交，并多次通过同一边。如ACBDCDEG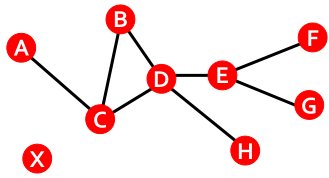

（1）图中的距离
距离(最短路径，大地测量法geodesic)：一对节点之间的距离定义为沿连接节点的最短路径的边数。
若两个节点不相连，则距离通常定义为无穷大或为0。
在有向图中，路径需要按照箭头方向来。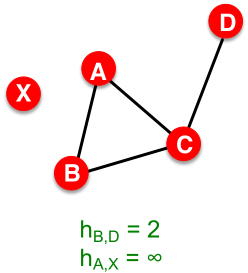

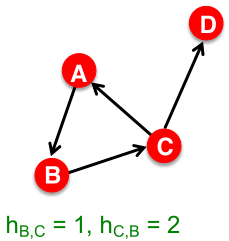
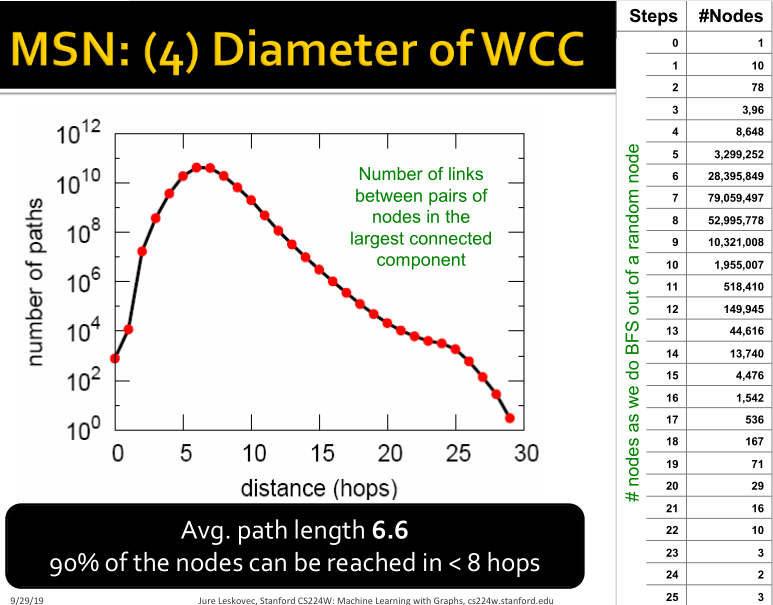
（2）网络直径
直径Diameter：图中所有节点之间的距离（最短路径）的最大值。
设是节点到节点的距离，最大边数（total number of node pairs），则平均路径长度为。（一般计算均值时，只看连接的节点。）
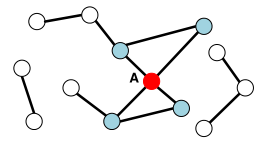
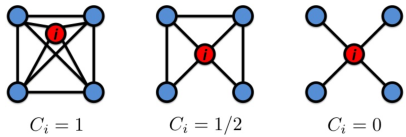
3、聚类系数-无向图
设节点的度为，定义，，其中是节点的邻居之间的边数。
节点度为的邻居之间的最大边数为。
节点度为0或1的聚类系数无定义，或定义为0。
平均聚类系数。

01&02 图模型的基本介绍 - 图62

01&02 图模型的基本介绍 - 图64

4、连通性

最大连接组件的大小：可以通过一条路径连接任何两个节点的最大的集合。
Largest component = Giant component

如何找到连接的组件？

开始随机找一个节点，执行广度优先搜索（Breadth First Search，BFS）；
给BFS访问过的节点标记记号；
如果所有节点都被访问过，则网络是连接的；
否则找到一个未被访问的节点，重复BFS。

3、真实网络的性质

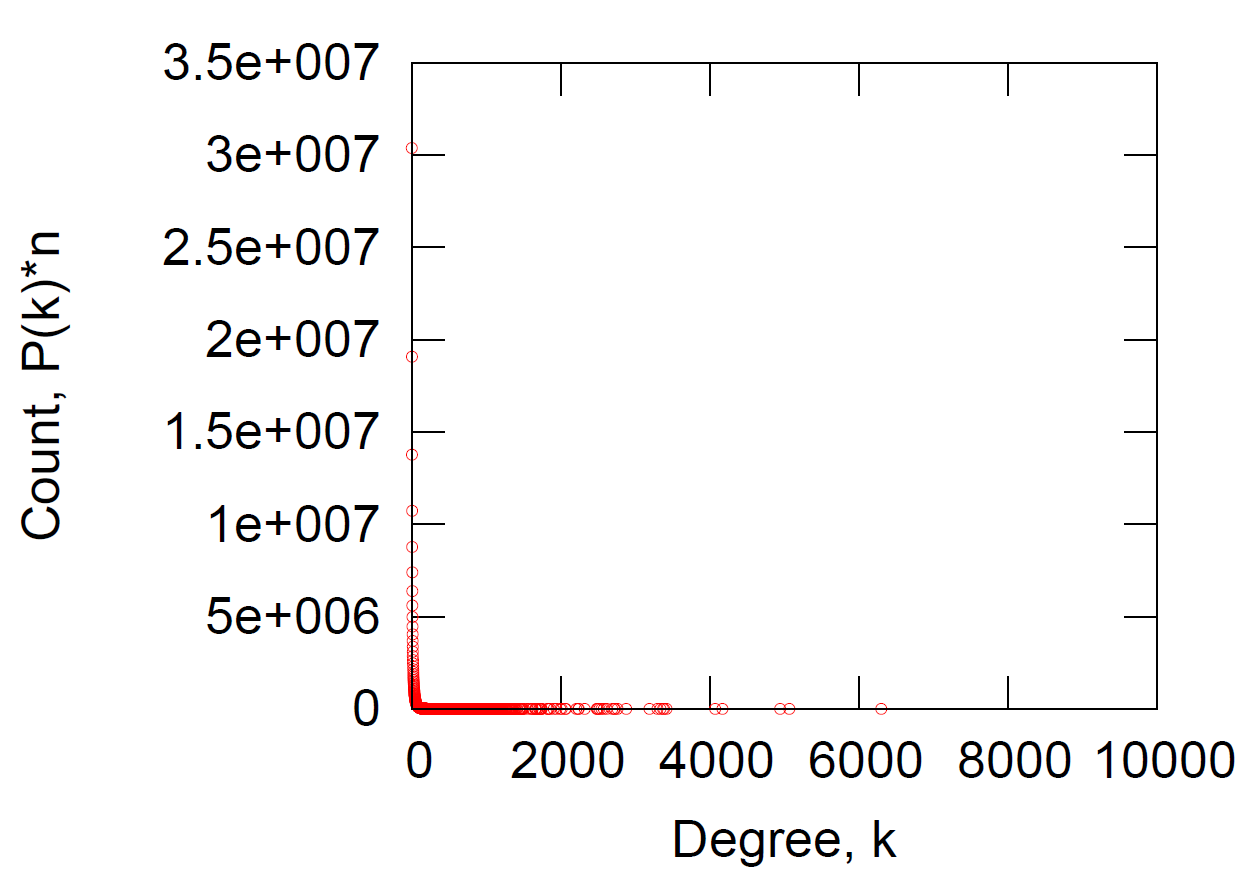
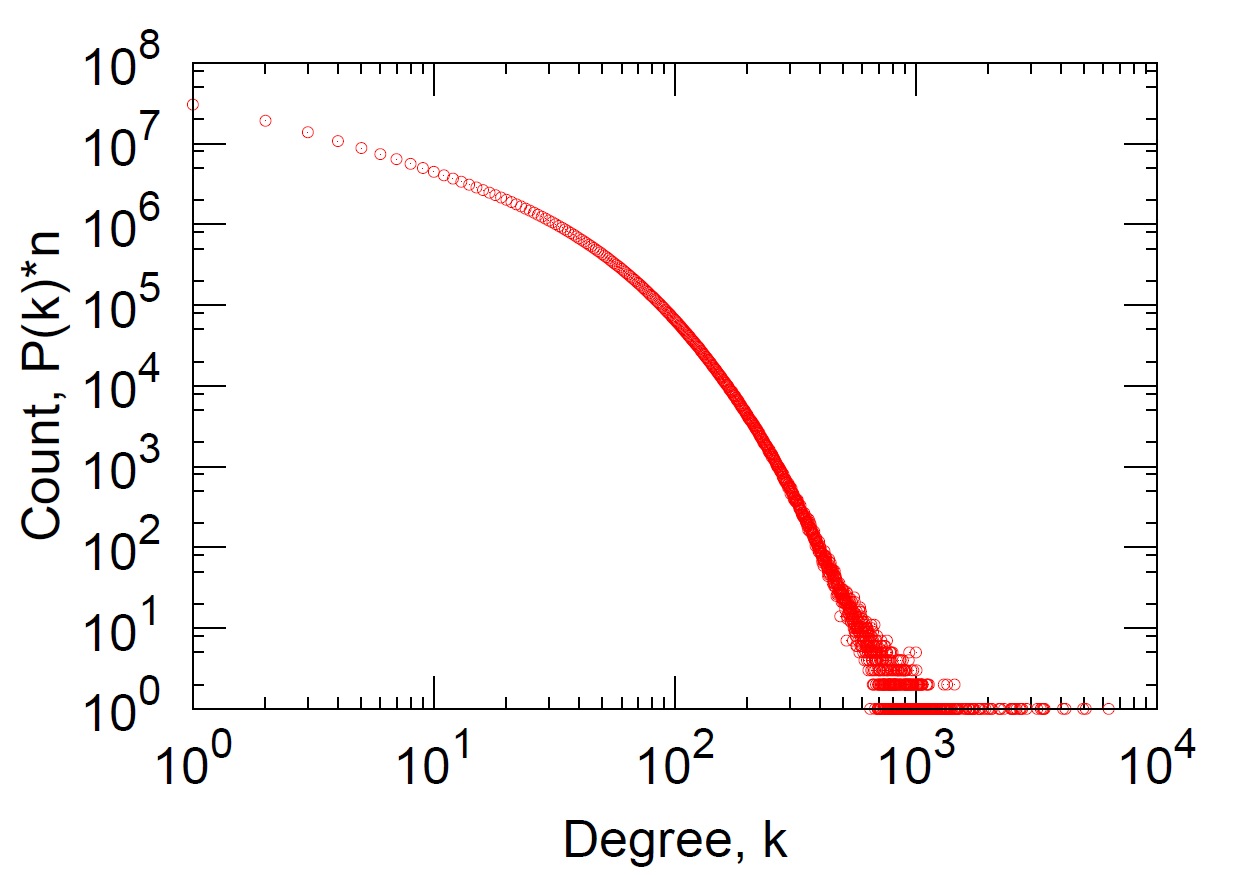
（1）MSN的度分布

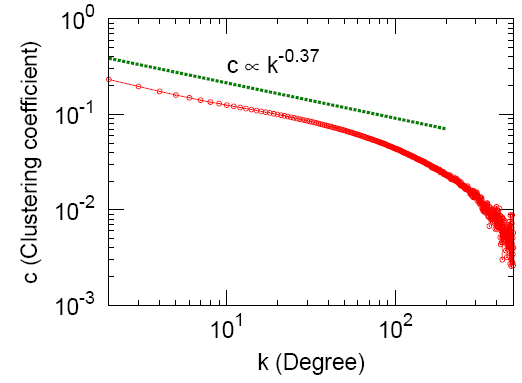
（2）聚类

节点的度为的平均：

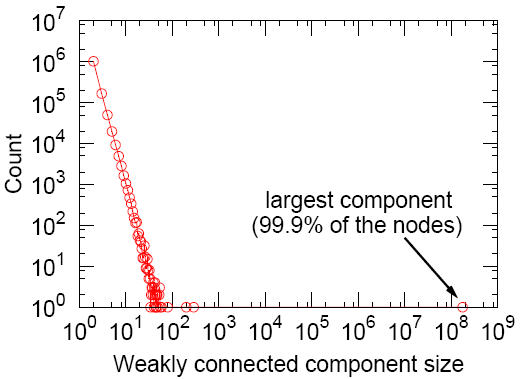
（3）连通分支

（4）WCC的直径

（5）MSN网络性质总结

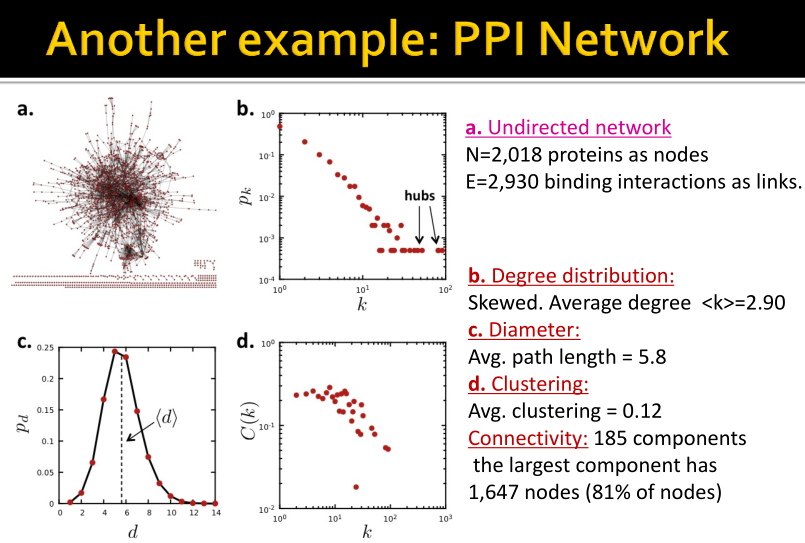
（6）PPI网络的性质

三、Erdos-Renyi随机图模型
两个变体：
：个节点的无向图，每条边以概率（i.i.d.）相连。
：个节点的无向图，随机选取条边相连。
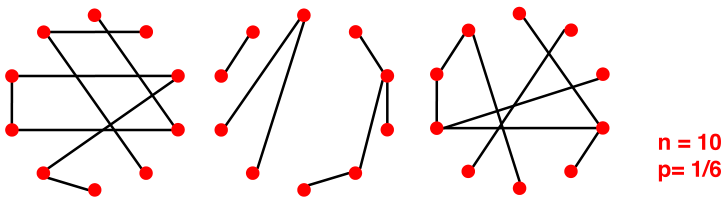
同样的和可以生成不同形式的图，因此和不能确定唯一的图，如下图所示：

（1）随机图模型的性质
的度分布、路径长度、聚类系数

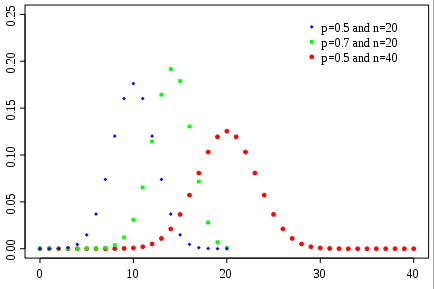
1）度分布
度分布是二项分布。设为节点度为的概率，则

，根据大数定律，随着网络越来越大，越来越相信每个节点的度数在附近。

2）聚类系数
设节点的度为，定义，，其中是节点的邻居之间的边数。
，其中表示度为的节点的邻居对数，表示每对节点以概率相连。

随机图的聚类系数很小

3）路径长度
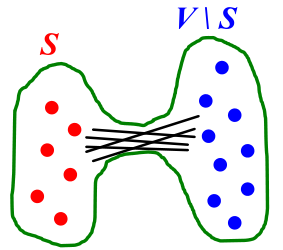
Graph has expansion :

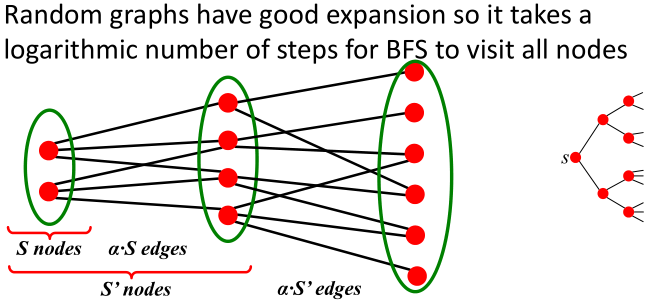
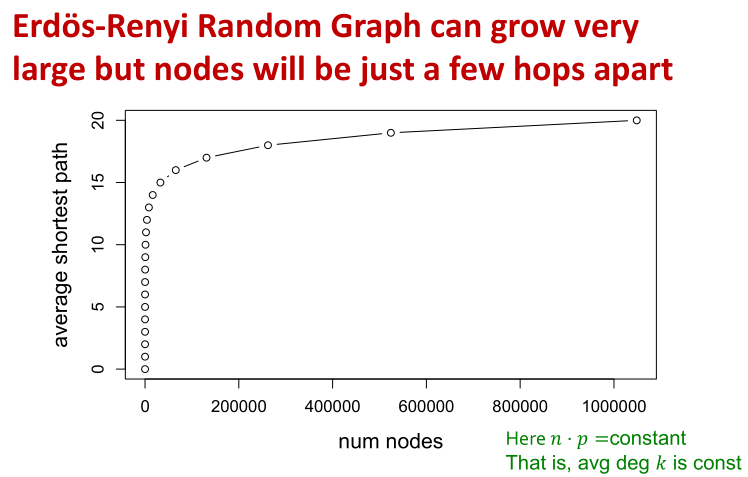
节点数为且expansion为的图，所有的节点对之间的路径长度为
对于随机图，由于，所以

4）连通分支
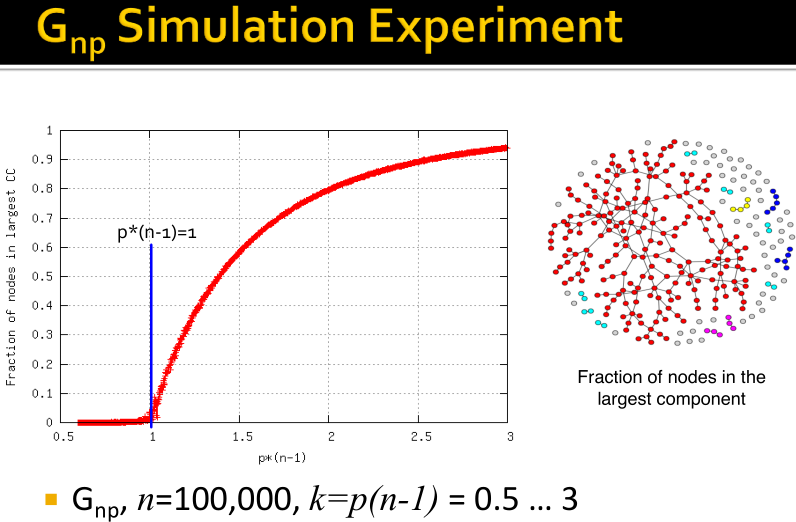
图结构随着概率的变化而变化，如下图所示，当时为空图，即没有边相连；当时为完全图，即任意两个节点之间均有边相连；当时，度的均值为，此时为连通图。

（2）MSN与随机图的性质比较

随机网络模型的缺点：
真实网络与随机网络模型的度分布不同；
Giant component in most real networks does NOT emerge through a phase transition；
没有局部结构，聚类系数太低。

随机网络模型的优点：

是其他类的参考模型；
帮助我们计算许多数值，可以与真实数据进行比较；
帮助我们了解某一特定属性在多大程度上是一些随机过程的结果。
四、The Small-World Model小世界模型

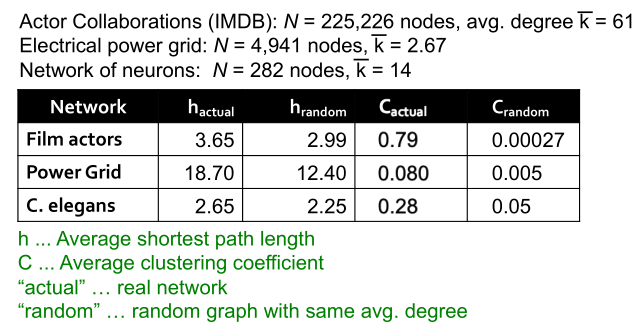
由上述分析可知，随机网络较好的模拟了真实数据中平均路径长度，但是却远远低估了聚类系数。在真实网络中，聚类系数应该是比较高的（比如说，朋友的朋友大概率也是我的朋友），因此希望可以有一种模型，在平均路径较小的条件下，聚类系数较高，就有了小世界模型。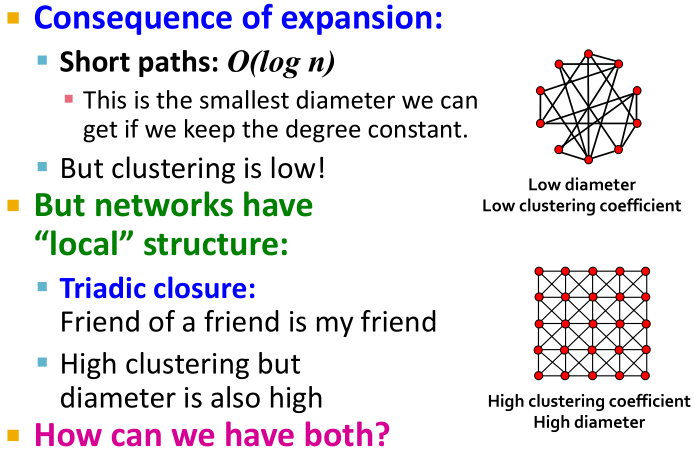

Small-World Model：
（1）首先产生一个标准网络，有较高的聚类系数，较大的直径，如下最左边的图所示；
（2）按照一定概率，将一条边的另一个端点连接到任意较远的节点上，如下图中间所示，这样仍然可以保持高聚类系数，但是图的直径减小了，即生成了小世界网络。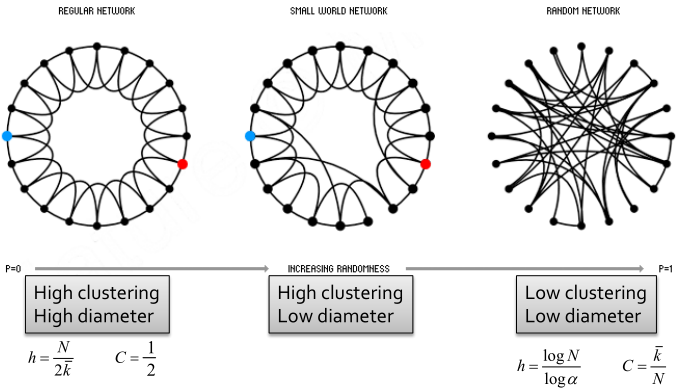

上图所示，左边为标准网络，中间为小世界网络，右边为随机网络，小世界网络可以有较高的聚类系数，较小的直径，但是小世界网络的度分布可能会有一定的偏差。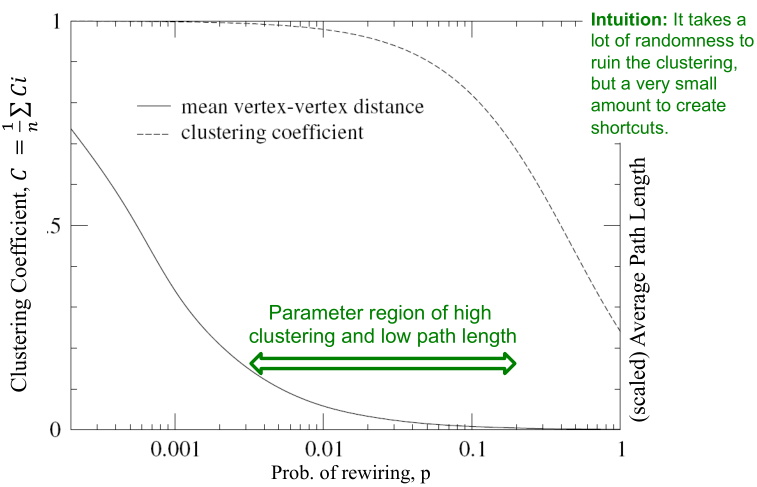

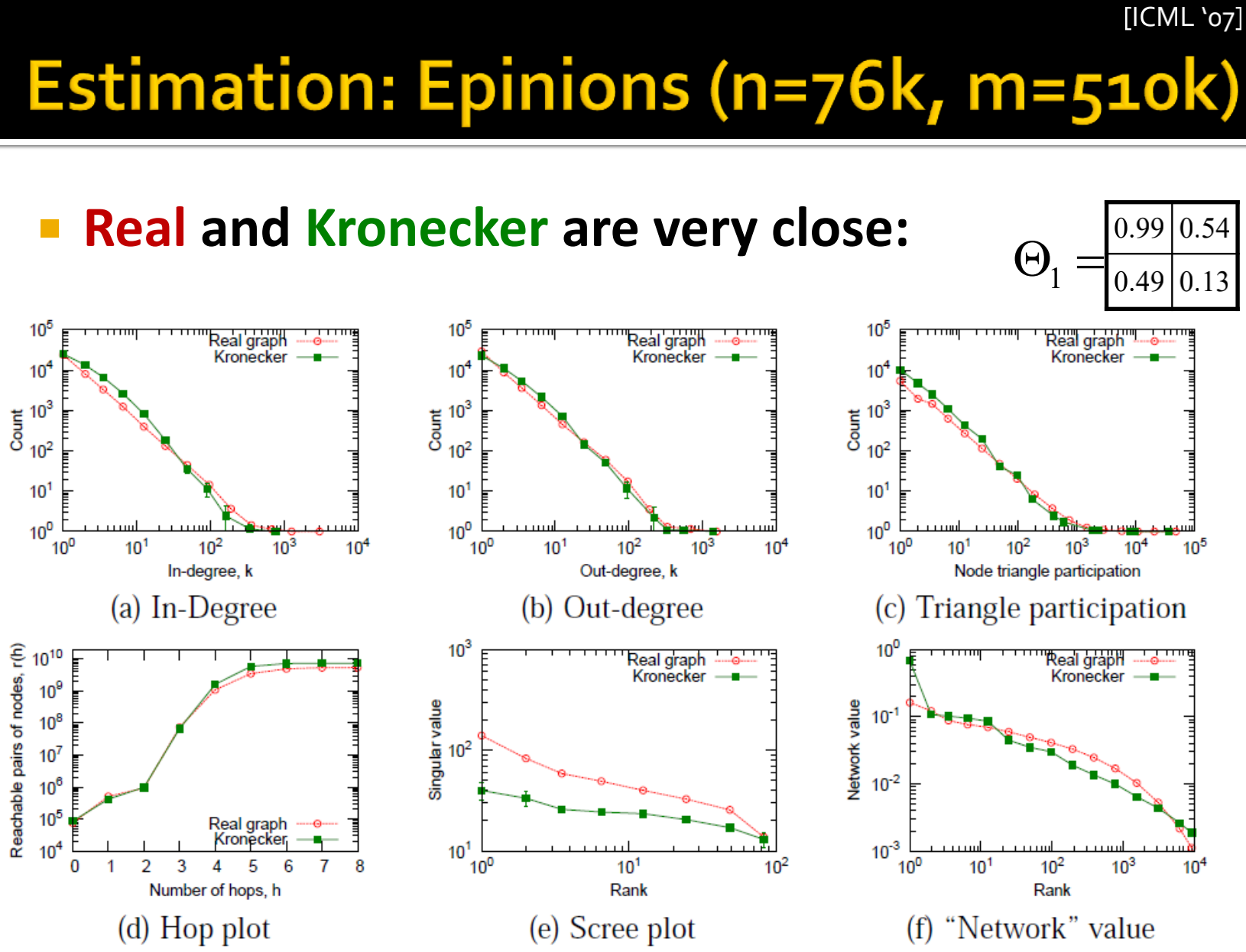
五、Kronecker Graph Model
可以利用Kronecker网络模拟大的真实网络，它的想法就是自相似度（self-similarity），就是利用Kronecker内积自己对自己迭代。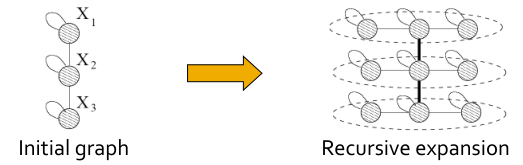

（1）Kronecker乘积

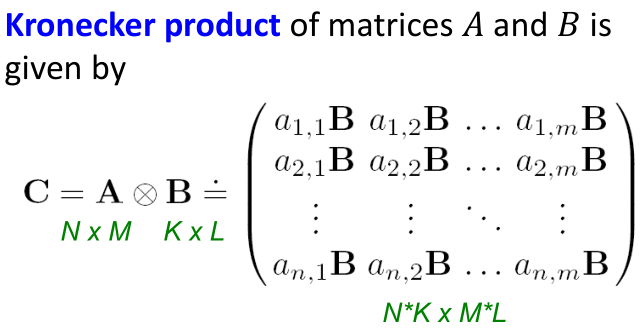
将两个图的Kronecker乘积定义为它们邻接矩阵（adjacency matrices）的Kronecker乘积。
（2）Kronecker图
Kronecker图是由Kronecker乘积在初始矩阵上迭代增长的图序列得到的，即：

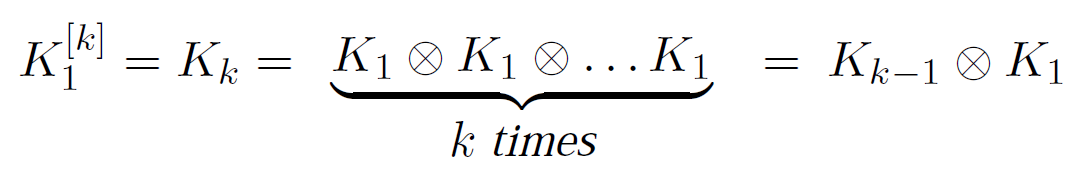
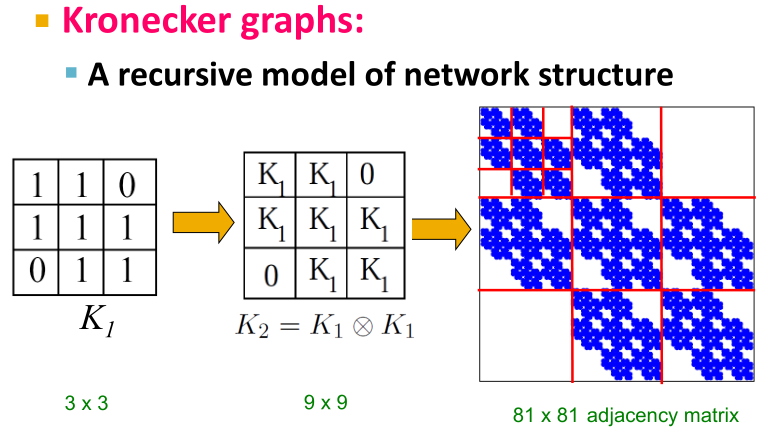
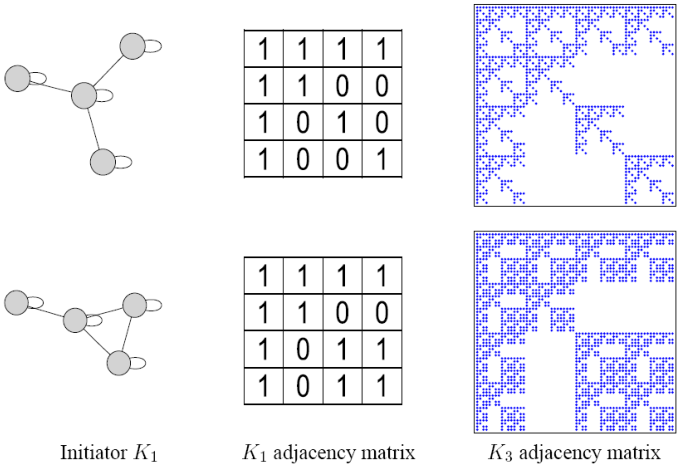
（3）随机Kronecker图

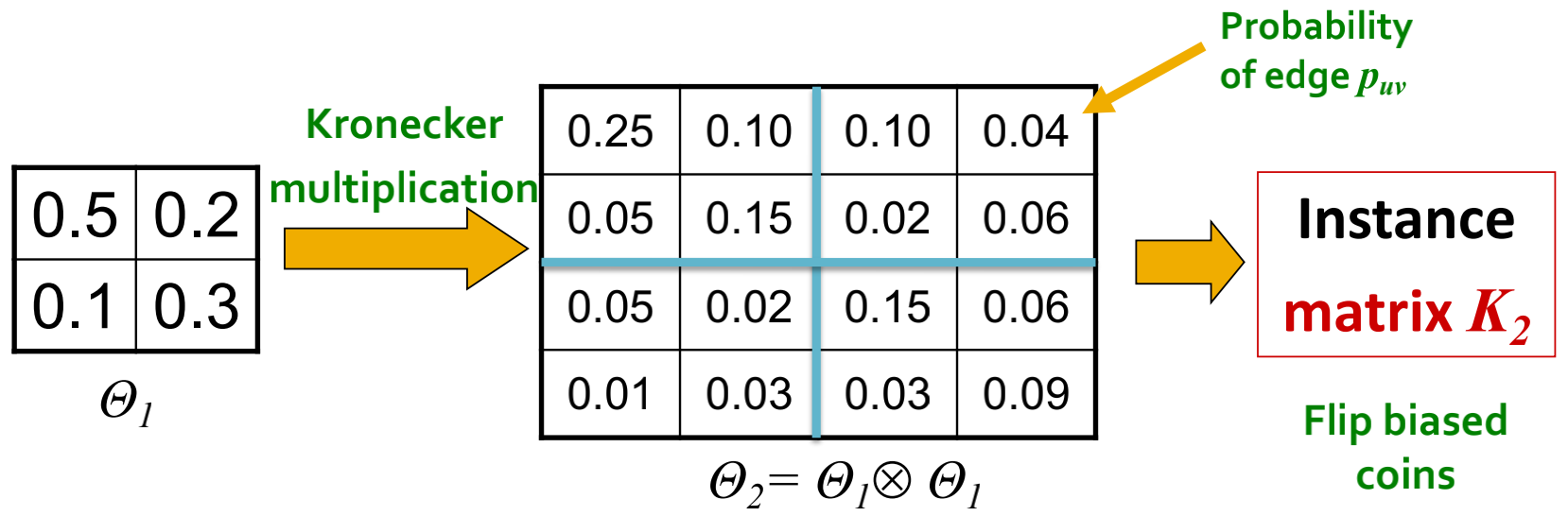
方法1

创建一个的概率矩阵；
计算次Kronecker乘积；
在中的表示在矩阵中边存在的概率，依据此概率矩阵即可得到最终的图。

方法2

上述生成随机Kronecker图的方法太慢了，可利用Kronecker图的递归结构来快速生成，将边逐个 “丢 “到图上。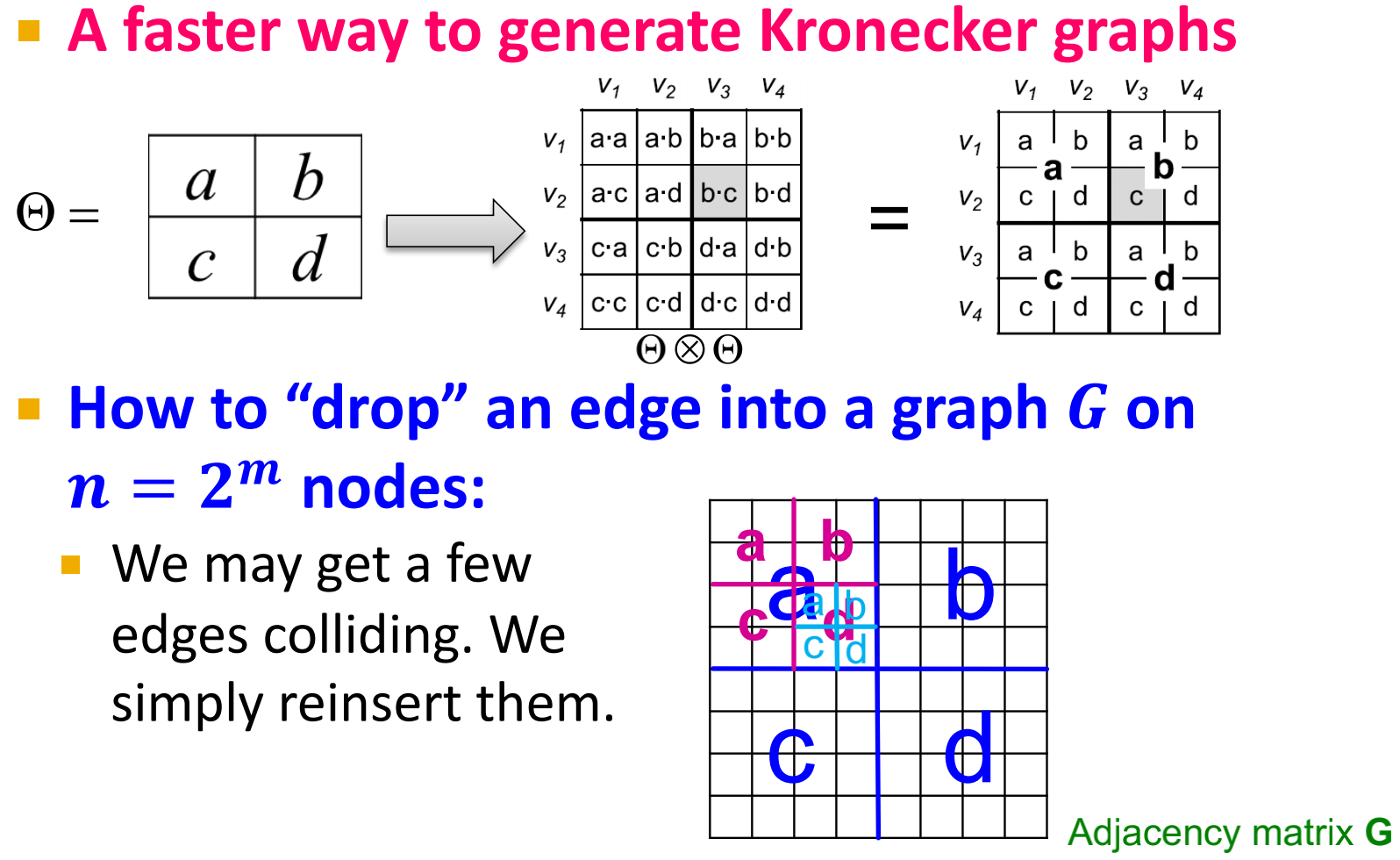

collide 碰撞；相撞；冲突；严重不一致
快速生成有向Kronecker图方法，具体见Kronecker Graphs: An Approach to Modeling Networks：
在节点数为 01&02 图模型的基本介绍 - 图156 的图 01&02 图模型的基本介绍 - 图157 上插入一条边：