介绍

图中的特征学习目的：基于图的机器学习的高效独立任务的特征学习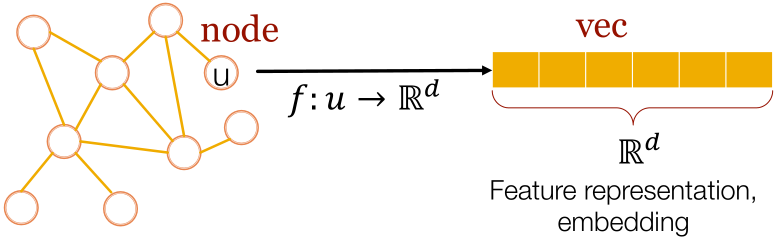

为什么使用网络嵌入？
任务：将网络中的每个节点映射为低维空间

• 节点用分布表示
• 节点之间embedding的相似性，表示它们的网络相似
• 编码网络信息，生成节点的表示

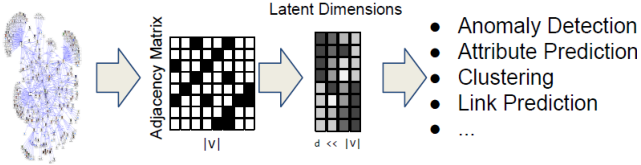
为什么难？
现代深度学习工具箱是为简单的序列或网格设计的，如对于固定大小的图像或网格的CNNs、文本或序列的RNNs或word2vec。
但是网络更复杂：

• 复杂的地形结构，如没有像网格那样空间局部性；
• 没有固定的节点排序或参考点(即同构问题)；
• 经常是动态的，且有多模态特征。

  Embedding Nodes

  假设我们有个图，顶点集合是，邻接矩阵是（假设是0-1），没有节点特征或额外信息被使用。
  目的：编码节点，因此嵌入空间（如点乘）的相似性近似于原始网络中的相似性。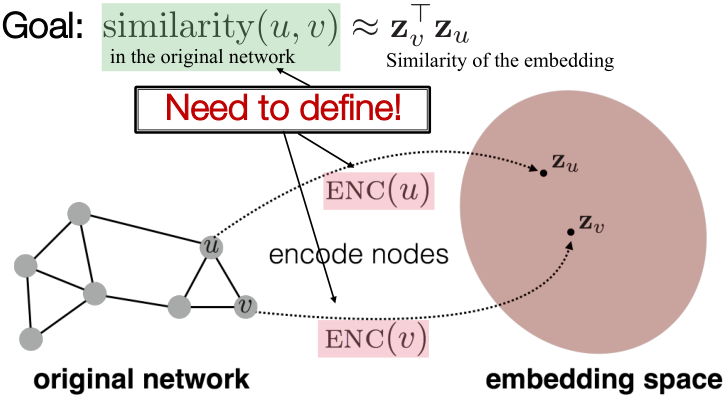
  

任务：

• 定义一个encoder，即从节点到embeddings的一个映射；
• 定义一个节点相似性函数，即与原始网络相似性的一个度量；
• 优化encoder的参数，使得

两个重要内容：

• Encoder：将每个节点映射为一个低维向量，，其中表示输入图的节点，是一个维embedding；
• 相似性函数：指定向量空间中的关系如何映射到原始网络中的关系。

Shallow Encoding：
最简单的编码方式：编码只是一个embedding-lookup，，
矩阵的每一列是一个节点的embedding（what we learn），
指示向量除了用1表示节点在列中外均为0。

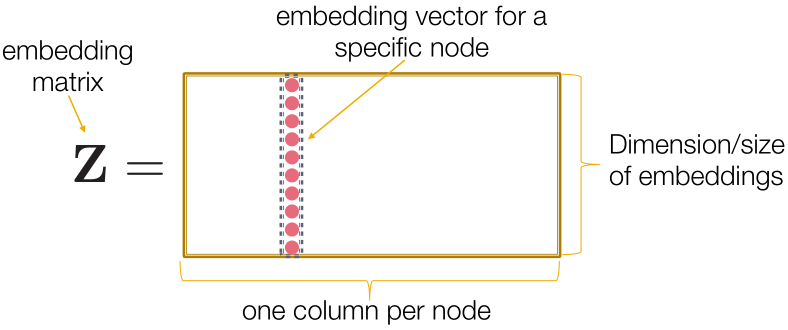
每个节点都被分配到一个独特的嵌入向量。
许多方法：DeepWalk、node2vec、TransE

如何定义节点的相似性？
选择方法的关键是该方法如何定义节点的相似性。
当节点有以下的情况时，两个节点是否应该有相似性？

• 相连；
• 有共同的邻居；
• 有相似的“结构角色”；

• …

  Random Walk Approaches to Node Embeddings

  Material based on:

• Perozzi et al. 2014. DeepWalk: Online Learning of Social Representations. KDD.

• Grover et al. 2016. node2vec: Scalable Feature Learning for Networks. KDD.

  Random Walk

  给定一个图和一个起点，随机选择该起点的一个邻点，并移动到这个邻点；然后随机选择这个点的一个邻点，并移动到它，等等。这样选择的（随机）点序列就是在图上的随机游走。
  

步骤：
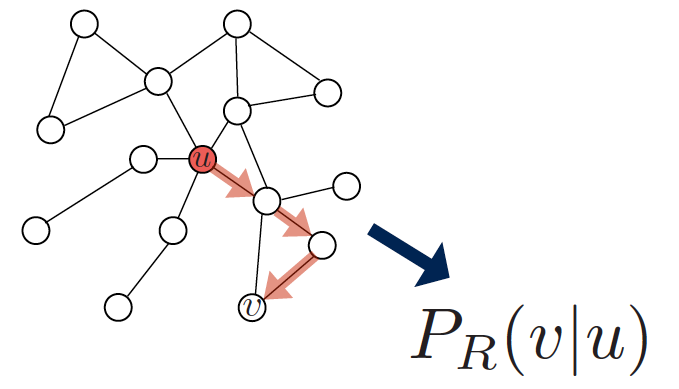
1、使用某种随机游走策略R，估计从节点开始的一个随机游走经过节点的概率；
2、优化embeddings来编码这些随机游走统计量：Similarity（此处） encodes random walk similarity。

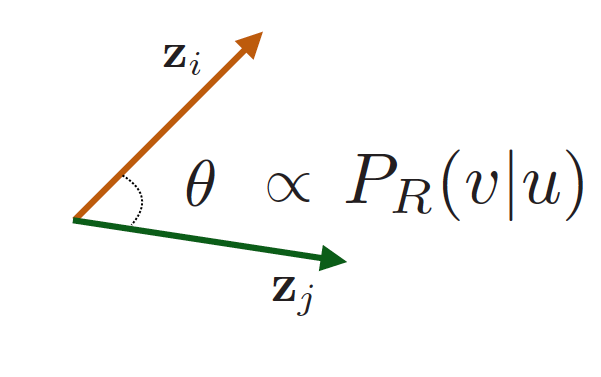
为什么使用随机游走？
1、Expressivity 表达上： 灵活地随机定义节点相似度，同时纳入局部和高阶邻域信息。
2、Efficiency 效率上：训练时不需要考虑所有的节点对，只需要考虑随机游走时共同出现的节点对。

无监督特征学习：
直观上， 找到节点到d维的嵌入，使之能保持相似性。
思想是学习使邻近节点在网络中靠得很近的节点嵌入。
给定一个节点，如何定义邻近节点？
是通过某种策略得到的节点的邻居。

特征学习作为优化：
给定，目标是学习一个映射，对数似然目标函数为，给定节点，我们想要学习对其邻域中的节点有预测性的特征表示。

随机游走的优化：
1、使用某种策略，从图的每个节点开始，运行固定长度的短距离随机游走；
2、对于每个节点，收集，即收集从开始随机游走所访问的节点的多个集合；
3、根据基于节点预测其邻域来优化嵌入，。
可以有重复的元素，因为节点能够通过随机游走被多次访问到。

优化嵌入，最大限度地提高随机游走共同出现的可能性。
使用softmax，是因为我们想要节点与节点更相似。

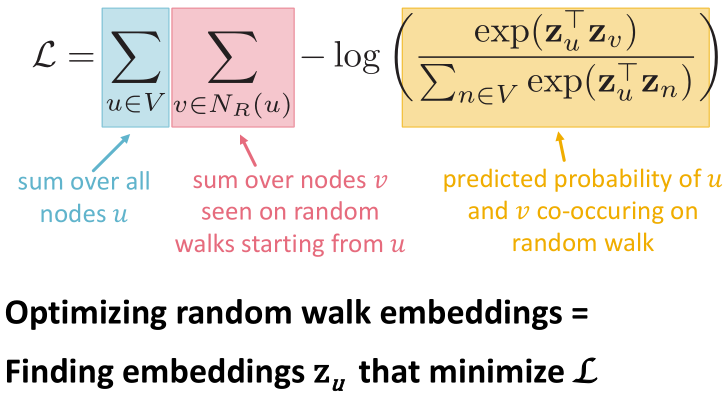
直接对进行优化，时间复杂度太高，为。
解决方法：negative sampling

为sigmoid函数，为随机分布。
不需要对所有节点进行归一化，只需要对个随机的 “负样本 “进行归一化。
样本个负结点与度数成正比。
的两个考虑：

• 更高的有更稳健的估计；
• 更高的对应着较高的负面事件偏差。

实际中
为什么约等于有效？
严格来说，这是不同的目标函数。但是Negative Sampling是噪声对比评估（Noise Contrastive Estimation，NCE）的一种形式，它近似于最大化Softmax的对数概率。新的表述对应于使用逻辑回归(sigmoid func.)将目标节点与从分布抽样得到的节点区分出来。更多请见https://arxiv.org/pdf/1402.3722.pdf。

以上介绍了如何基于给定的随机游走统计量来优化嵌入，那么有什么技巧能够用来运行随机游走呢？
最简单的想法： 只需从每个节点开始，运行固定长度、无偏的随机行走即可。DeepWalk from Perozzi et al., 2013
问题是，这种相似性的概念过于拘谨。如何推广这个想法呢？

node2vec

目标：将相似网络邻域的节点嵌入到特征空间中，使之接近。
我们把这个目标框定为一个最大似然优化问题，与下游预测任务无关。
关键：节点的网络邻域概念导致丰富的节点嵌入。
开发有偏的二阶随机游走，生成节点的网络邻域。

思想：使用灵活的、有偏的随机游走，可以在网络的局部和全局观点之间进行权衡。（Grover and Leskovec, 2016）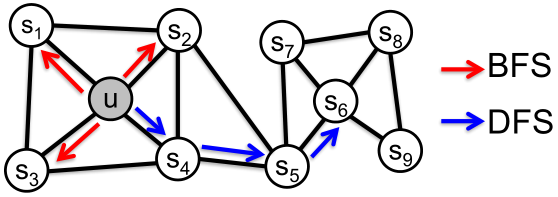

定义一个给定节点的邻域的两种经典策略：BFS、DFS。
步长为3（的大小为3）：

• ，局部微观视角
• ，全局宏观视角

给定一个节点产生邻域的有偏定长随机游走，两个参数：

• 返回参数。返回前一个节点。
• 输入输出参数。进（DFS）与退（BFS）；直观地说，是BFS与DFS的 “比率”。

有偏二阶随机游走探索网络邻域：
如下左图所示，随机游走穿过边，现在是在处（从走到）。的邻居可以如下左图所示，要记住从哪里走来的。
右下图中的都是未标准化的概率，其中是模型转移概率，是返回参数，是走开参数。

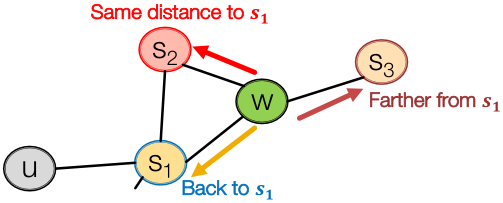
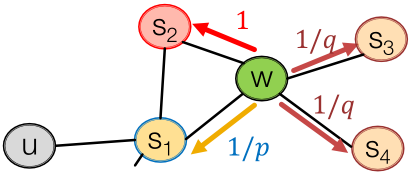
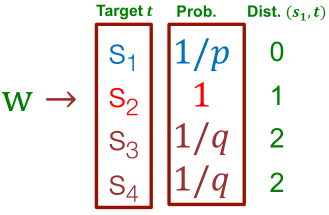非标准化的转移概率，根据与的距离来划分。

• BFS方式游走：低值；
• DFS方式游走：低值。

是通过有偏游走所访问到的节点。

node2vec算法：
（1）计算随机游走的概率；
（2）从每个节点开始，模拟长度为的个随机游走；
（3）使用随机梯度下降法优化node2vec目标。
该算法的时间复杂度是线性的，上述三个步骤均可单独并行。

如何使用Embeddings

如何使用节点embeddings？

• 聚类/社区检测：聚类点；
• 节点分类：基于预测节点的标签；

• 链接预测：基于预测边。在这里可以用连接、均值、乘积或者取embeddings的不同，具体地：

  • concatenate：
  • Hadamard：
  • Sum/Avg：
  • Distance：

    小结

    基本思想：嵌入节点，使嵌入空间的距离反映出原始网络中节点的相似性。
    节点相似性的不同概念：

• Adjacency-based

• Multi-hop similarity definitions
• Random Walk approaches

所以应该使用哪一种方法呢？
没有一种方法能够解决所有的问题，如node2vec在节点分类上表现更好，而multi-hop方法在链路预测上表现更好（Goyal and Ferrara, 2017 survey）。
随机游走方法一般效率较高。一般情况下，必须选择与你的应用相匹配的节点相似性定义！

TransE:Translating Emeddings for Modeling Multi-relational Data

一个知识图谱嵌入的应用 Bordes, Usunier, Garcia-Duran. NeurIPS2013.
知识图谱（Knowledge Graph，KG）是由关于相互关联的实体的事实/陈述组成。节点是实体，边是关系。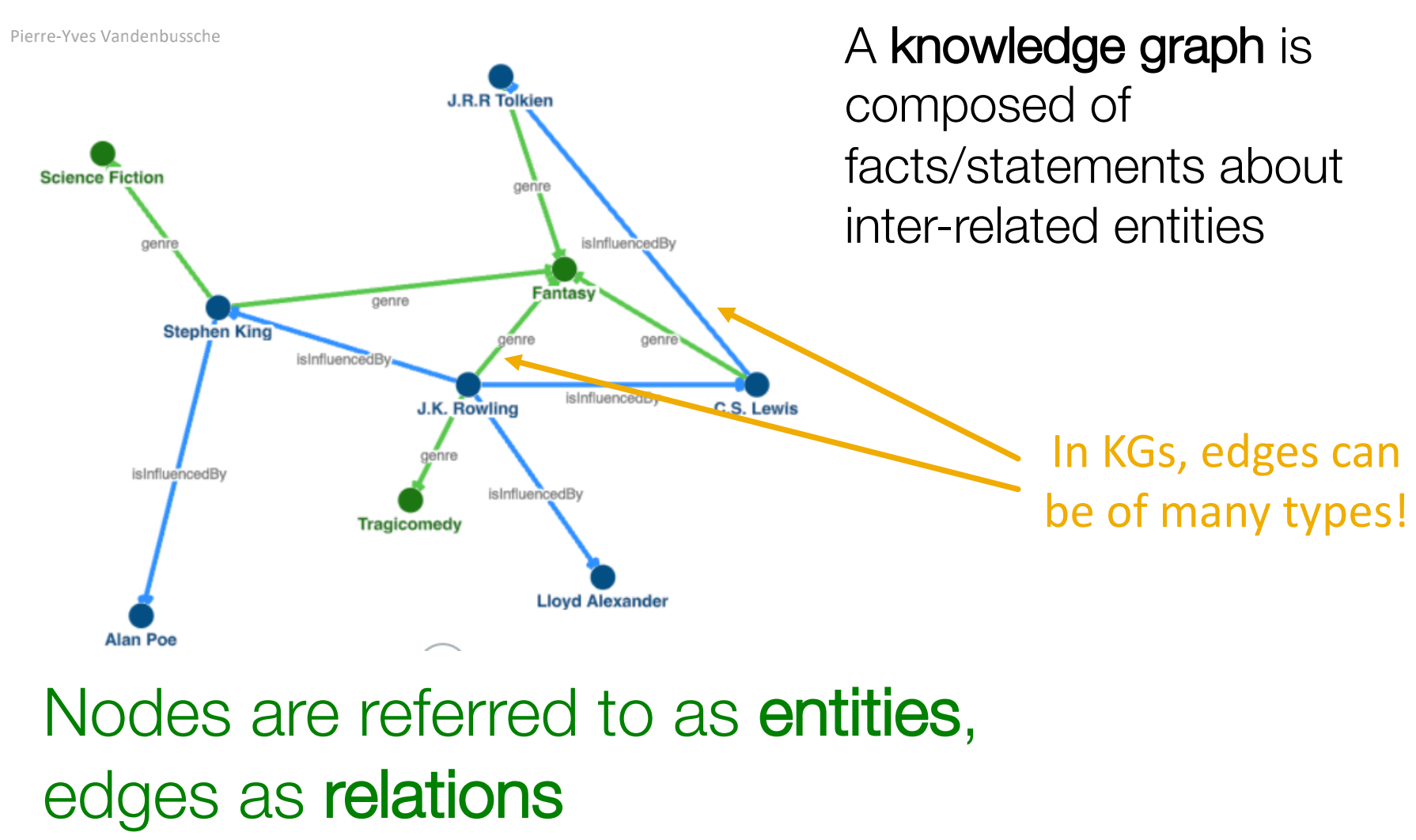

KG的不完整性会大大影响依赖它的系统的效率！KG Completion（链接预测）：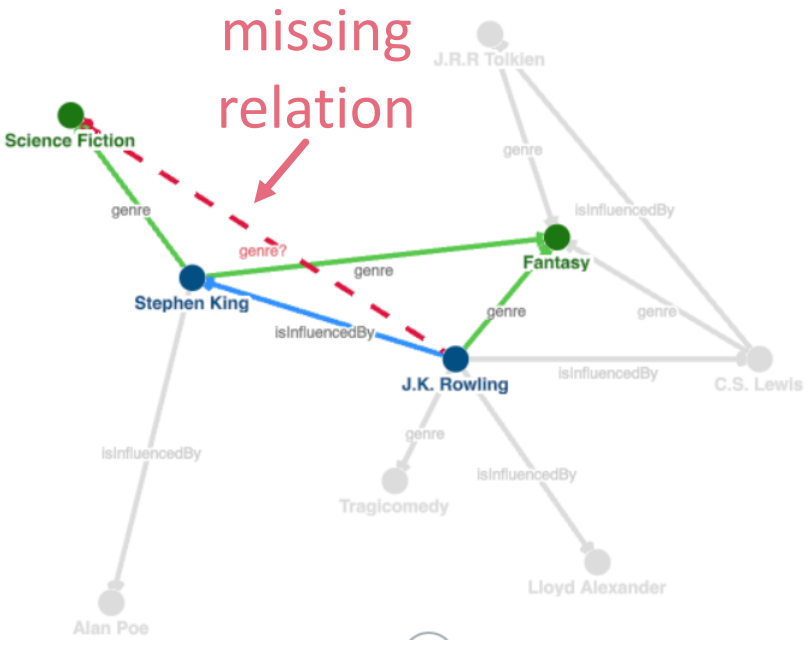

我们希望有一个链接预测模型，它能从KG的局部和全局连接模式中学习，同时考虑到不同类型的实体和关系。
下行任务：关系预测是通过使用学习到的模式来概括观察到的感兴趣的实体和所有其他实体之间的关系。
Translating Embeddings (TransE):
在TransE中，实体之间的关系用三联体来表示，即h(head entity), l(relation), t(tail entity) => (h, l, t)。
与先前方法类似，实体首先被嵌入一个实体空间。关系由平移表示：当事实是真的，；否则，。

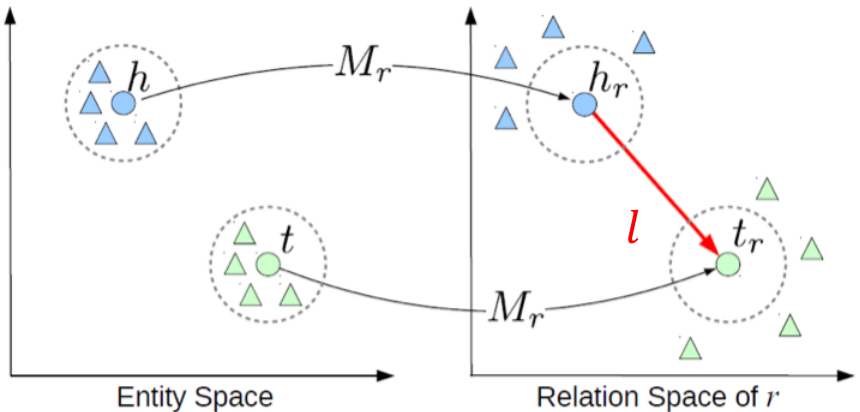
TransE Learning Algorithm:
输入：
训练集，实体集合E，关系集合L，边缘，嵌入维度。
初始化（实体随机初始化，关系标准化）：

循环：

终止循环。

Negative sampling with trilpet that does not appear in the KG.
是正样本的，是负样本的。
比较损失：有效的三元组有较低的距离值，而损坏的三元组有较高的距离。

Embedding Entire Graphs

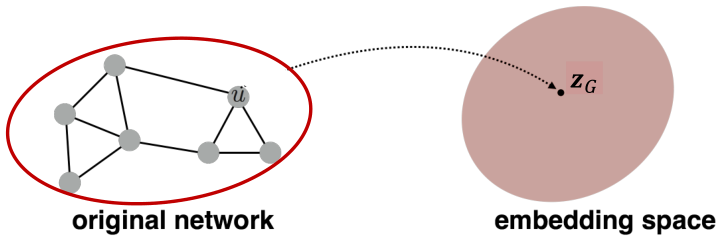
目标：对整个图进行embedding。
任务：（1）有毒分子与无毒分子的分类；（2）识别异常图。

方法1

Convolutional Networks on Graphs for Learning Molecular Fingerprints，Duvenaud等人2016年用于根据分子的图结构进行分类。

• 在（子）图上使用一个标准的图嵌入技术；

• 在（子）图上对节点的embeddings求和或求均值，；

  方法2

  Gated Graph Sequence Neural Networks，Li等2016年提出的一种子图嵌入的通用技术。引入 “虚拟节点 “来表示（子）图，并运行标准的图嵌入技术。
  

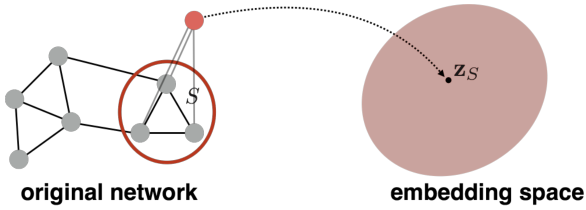
  方法3

  Anonymous Walk Embeddings, ICML 2018
  匿名行走中的状态，对应于我们在随机游走中第一次访问节点的索引。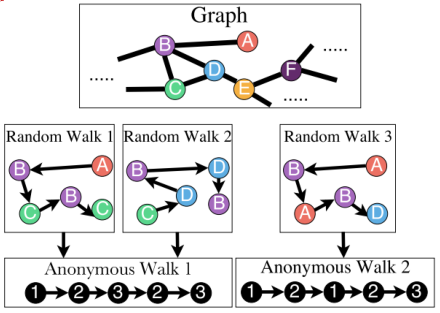
  
  
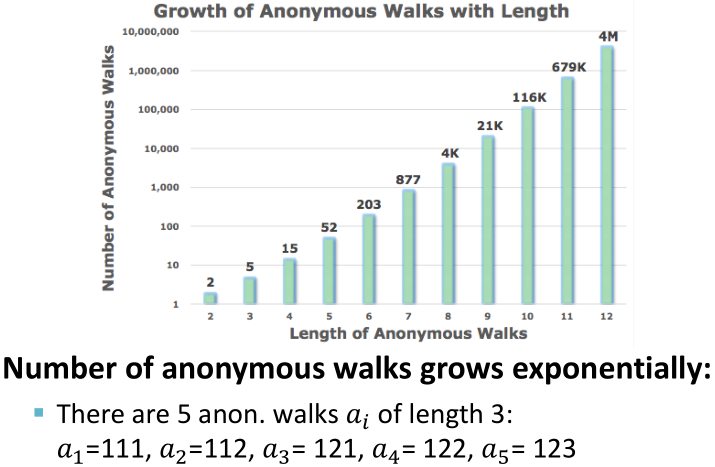
  当Anonymous Walks的长度为3时，有5种不同的情况：

• 

• 
• 
• 

Idea1 of Anonymous Walks

• 枚举所有可能的步长为的匿名游走，并计数；
• 基于这些游走，将图表示成概率分布。

如：

• 设；
• 将图表示成5维的向量，则长度为3的匿名游走有：

• 表示在G中匿名游走的概率。

  Idea2 Sample Anonymous Walks

  在一个大图中，完全计算所有的匿名游走可能是不可行的。考虑用抽样的方法来逼近真实分布，即独立生成一组m个随机游走，并计算其相应的匿名游走的经验分布。
  m该如何取值呢？我们希望分布的误差大于，概率小于：，其中表示步长为的匿名游走的总数量。
  如，，设，则我们需要个随机游走。

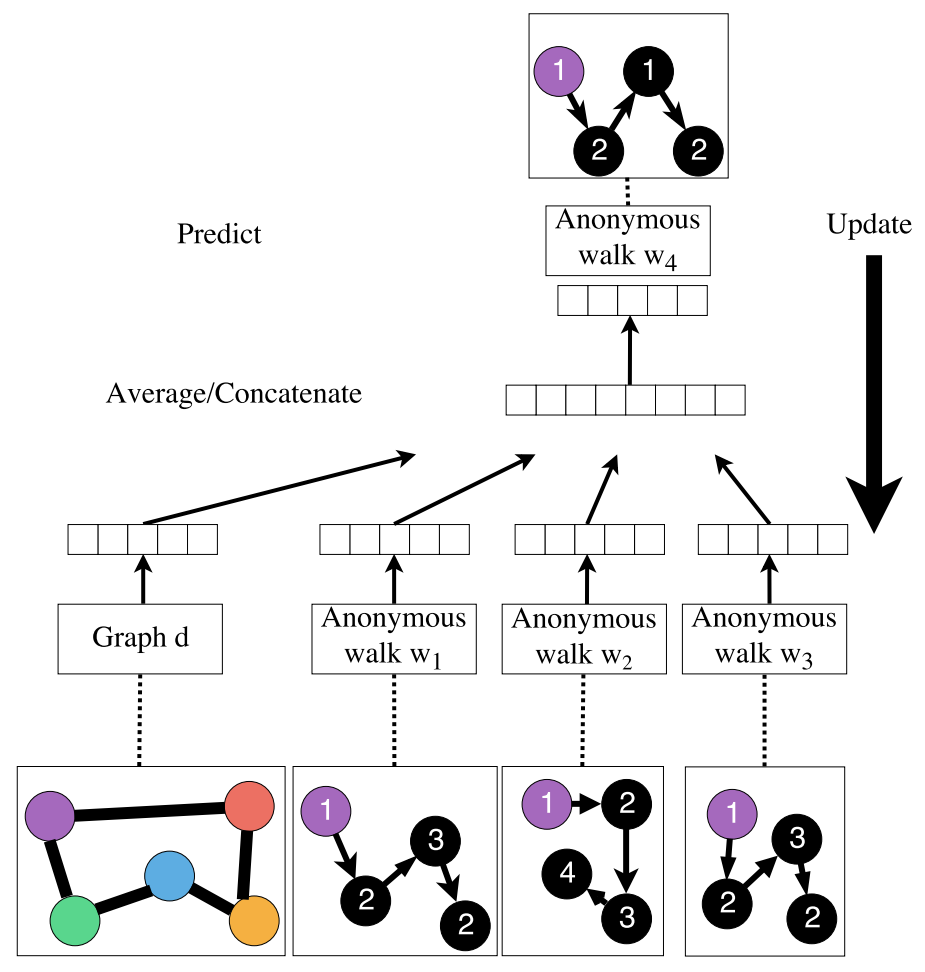
  Idea3 Learn Walk Embeddings

  对每个随机游走学习embedding，图的embedding与游走embedding进行sum/avg/concatenation。
  如何嵌入游走？Embed walks s.t. next walk can be predicted. 设 s.t.，极大化，其中表示第次随机游走的起点在节点处。
  

• 从节点处运行个每次长度为的不同随机游走：，设为游走的匿名形式。

• 学习预测游走在窗口同时出现
• 估计的匿名游走的嵌入：，其中表示文本窗口的大小。

，其中，，是的embedding。

总结

介绍了三种图嵌入方法：

• 方法1，嵌入节点，之后对它们求和或求均值
• 方法2，创建跨越(子)图的超级节点，然后嵌入该节点
• 方法3，（Idea1）通过所有匿名游走的分布来表示该图；（Idea2）抽样游走来近似分布；（Idea3）嵌入匿名游走。

  参考链接

  知乎笔记：https://zhuanlan.zhihu.com/p/141232377
  PPT：http://web.stanford.edu/class/cs224w/slides/07-noderepr.pdf