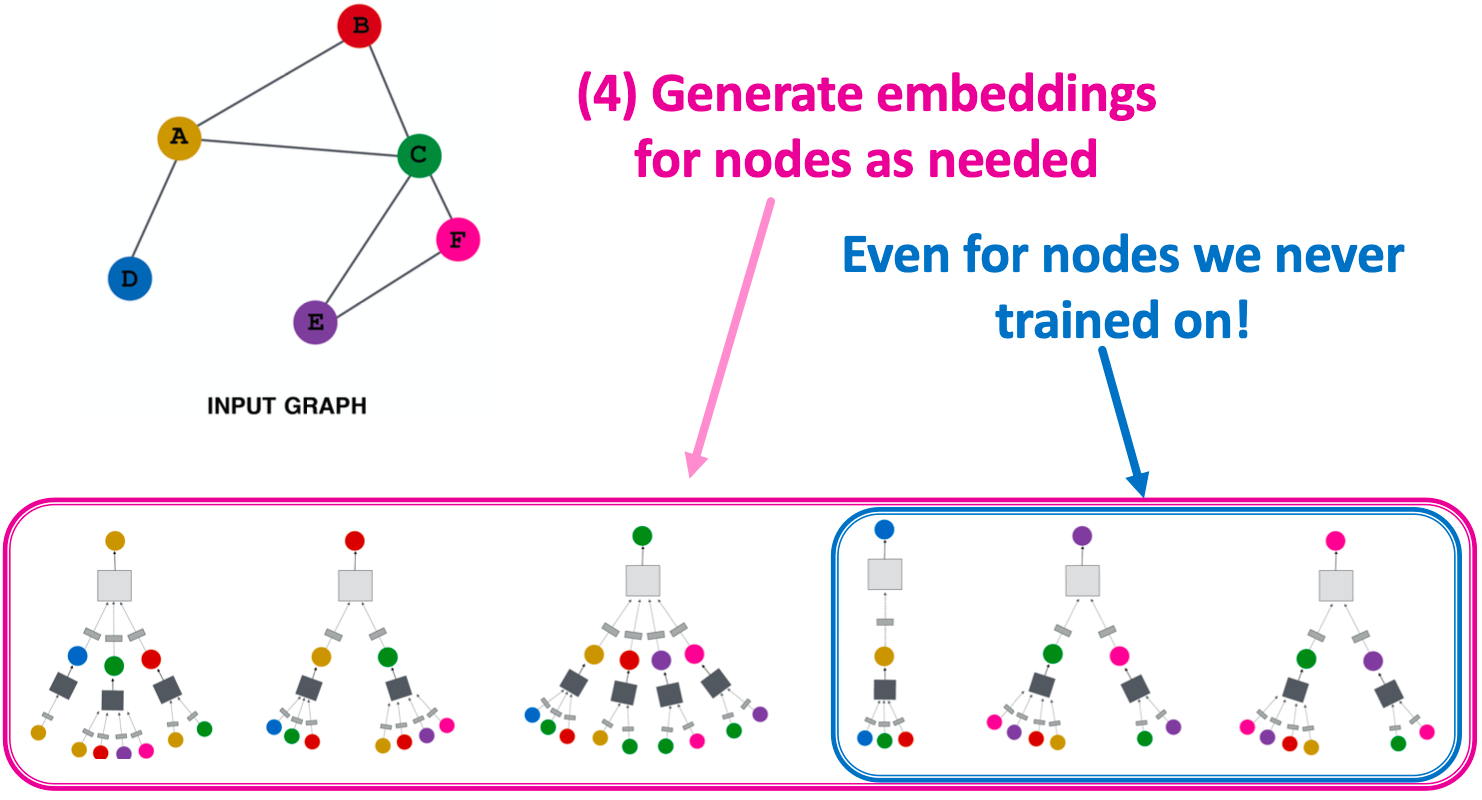
回顾

节点嵌入，直观上是将节点映射到维嵌入，这样，图中的相似节点被紧密地嵌入在一起。

Encoder：将每个节点映射为低维向量，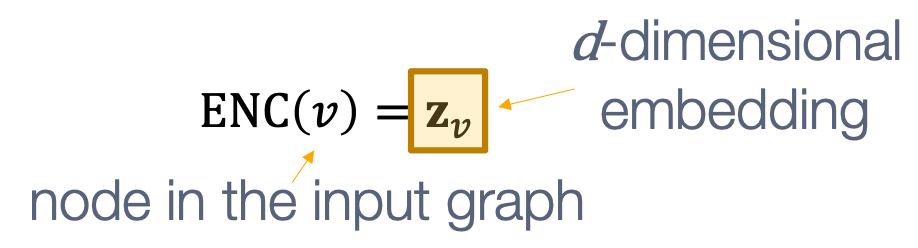
Similarity函数：指定向量空间中的关系如何映射到原始网络中的关系，
最简单的encoding方法：encoder仅是一个嵌入查询，如下所示：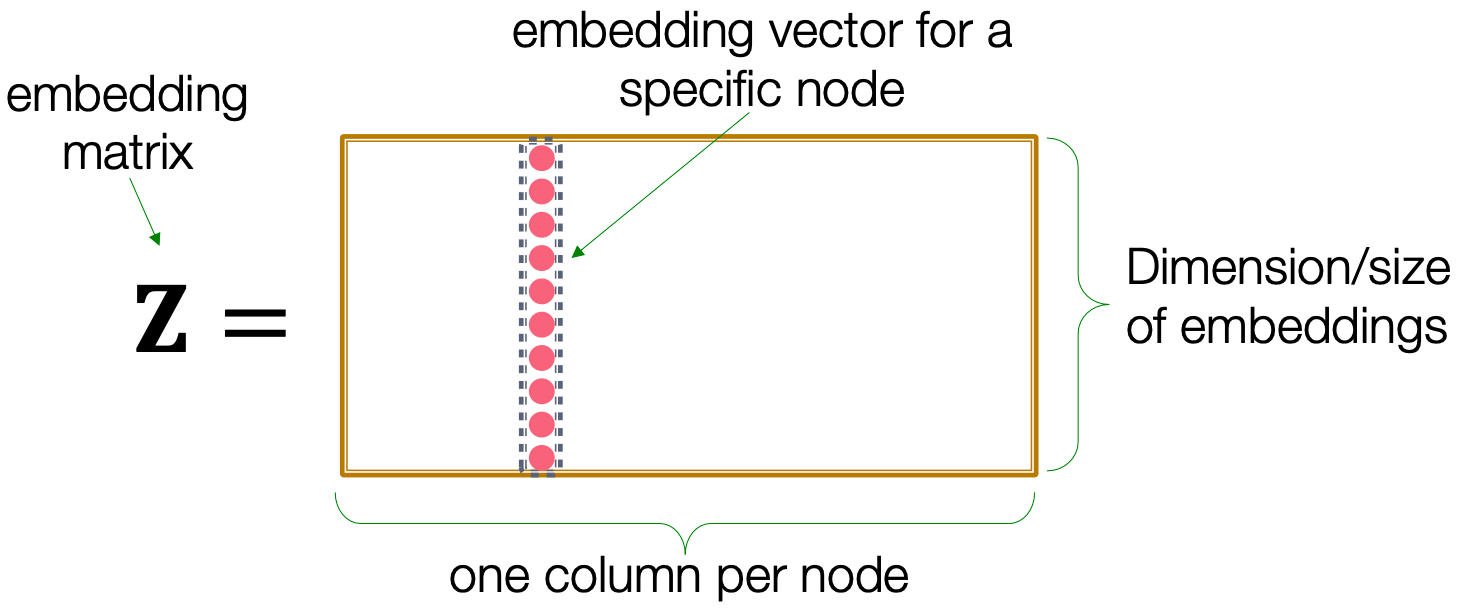

shallow嵌入方法的局限性：

• 需要参数。节点间没有共享参数，每个节点都是独有的嵌入。
• Inherently “transductive”（本质上是直推式）。在训练中没有的节点，不能生成节点嵌入。

• 不包含节点特征。许多图都具有我们可以并且应该利用的特征。

  Deep Graph Encoders

  接下来介绍基于graph neural networks(GNNs)的方法。
  基于图结构的多层非线性转换。
  注：所有这些深度编码器都可以与lecture3中定义的节点相似函数结合使用。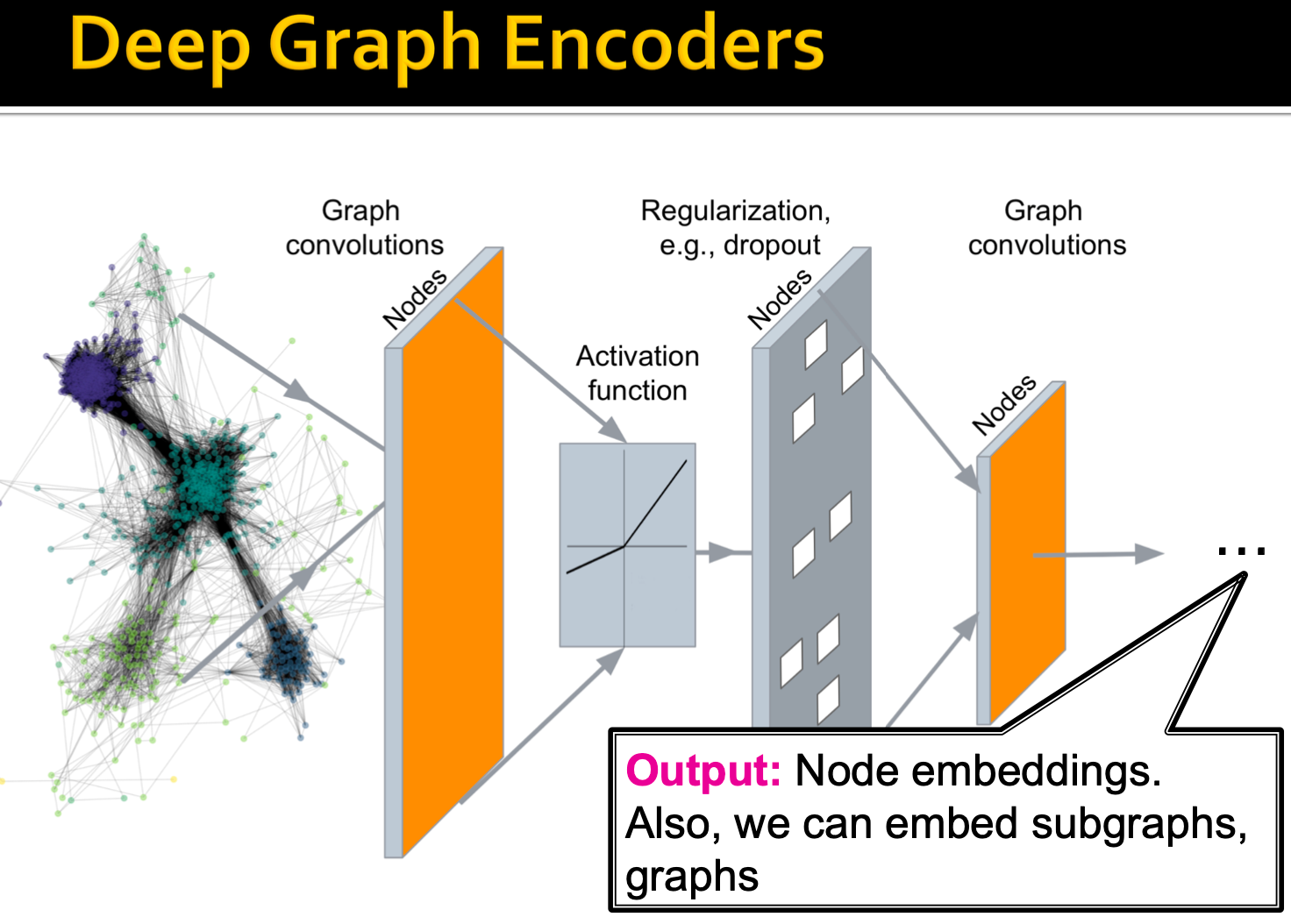
  
  Tasks on Networks：

• Node classification：给定节点预测类别；

• Link prediction：预测两个节点是否连接；
• Community detection：识别密集连接的节点集群；
• Network similarity：两个(子)网络有多相似。

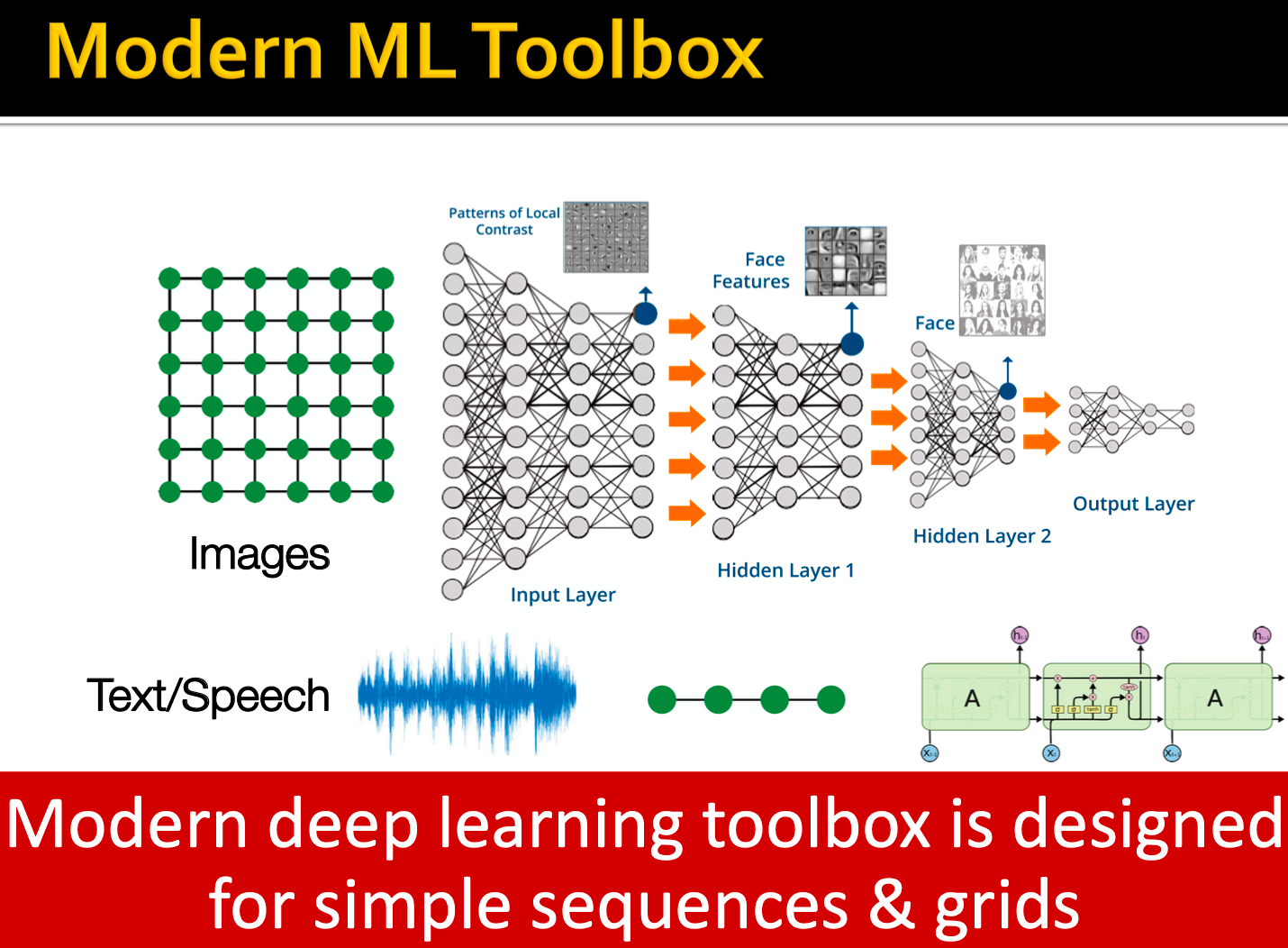
现代ML、DL是对简单序列/网格而设计的，但是网络更为复杂。网络是任意大小和复杂的拓扑结构(例如，没有像网格那样的空间局部性)：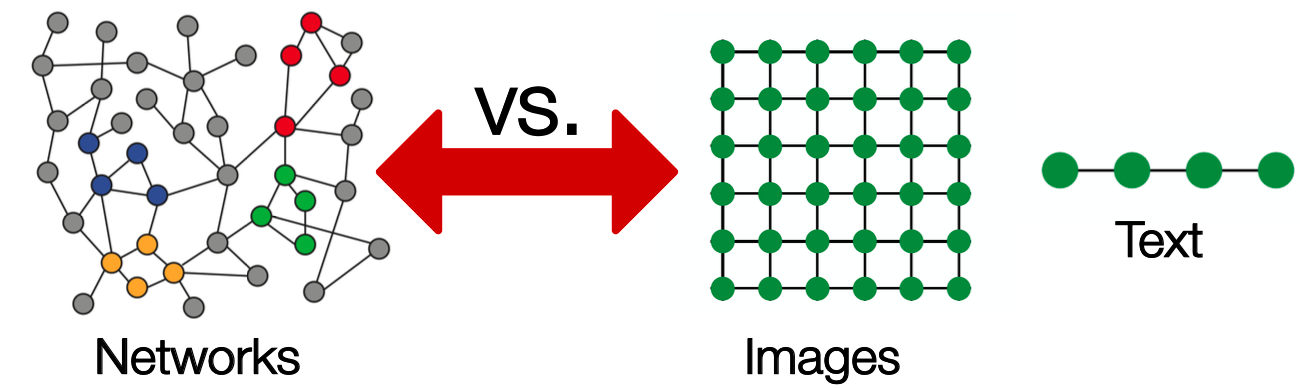

没有固定的节点排序或参考点，通常是动态的，具有多模态特性。

本节要点

• Basics of deep learning
• Deep learning for graphs

• Graph Convolutional Networks and GraphSAGE

  Basics of deep learning

  有监督学习：给定输入和目标，预测标签。
  输入可为：真实数值向量、序列（自然语言）、矩阵（图像）、图（可能带有节点和边特征）。
  将任务规划为一个优化问题：
  ：一组优化的参数，可以包含一个或多个标量、向量、矩阵……，如　在浅编码器中(嵌入查找)。
  ：损失函数。如L2损失，。其他常见损失函数，如L1损失、huber损失、max margin (hinge loss)、cross entropy……，可参考https://pytorch.org/docs/stable/nn.html#loss-functions

  损失函数例子

  一个常见的分类损失：交叉熵(CE)。标签是一个分类向量（one-hot编码），如，是第3类。
  ，，表示第几类，表示函数的向量输出的𝑖-th坐标。如。
  ，，是𝑖-th类的实际值和预测值。直觉上，损失越低，预测就越接近one-hot。
  所有训练例子的总损失：，是包含所有对数据和标签的训练集。

  如何优化目标函数？

  梯度向量Gradient vector：梯度最快增长的方向和速率，，是中的元素。
  一个多变量函数(如)沿给定向量的方向导数表示该函数沿向量的瞬时变化率，梯度是在最大增加方向上的方向导数。

  Gradient Descent

  迭代算法：在梯度方向(相反)反复更新权值，直到收敛，。
  训练：迭代优化，迭代为1 step of gradient descent。
  学习率(learning rate, LR) ：控制梯度步长大小的超参数，在训练过程中可调整变化。
  理想的终止条件：0梯度。在实践中，如果它不再提高验证集的性能，我们就停止训练(我们从训练中保留的数据集的一部分)。

  Stochastic Gradient Descent (SGD)

  gradient descent的问题：
  准确的梯度需要计算，其中是整个数据集，这意味着对数据集中所有点的梯度贡献求和，现代数据集通常包含数十亿个数据点，每一步梯度下降都非常费时。
  解决方法：随即梯度下降SGD，在每一步，选择一个包含数据集子集的不同minibatch ，将其作为输入。
  Batch size：小批处理(minibatch)中的数据点数量，如用于节点分类任务的节点数。
  Iteration：一个小批量SGD的1步。
  Epoch：一次完整遍历数据集(# iterations=数据集大小除以批处理大小)
  SGD是全梯度的无偏估计，但并不能保证收敛的速度，在实践中经常需要调整学习率。改进SGD的通用优化器，如Adam、Adagrad、Adadelta、RMSprop等。

  Neural Network Function

  目标：
  在深度学习中，函数可以是复杂的。简单起见，考虑线性函数，

• 若返回一个标量，则是一个可学习的向量，

• 若返回一个向量，则是一个权重矩阵，，的Jacobian矩阵。

  反向传播

  更复杂的函数：，也即。
  链式法则有：，如。
  反向传播：利用链式法则传播中间步的梯度，最终得到的梯度，记为。
  例子（简单的2层线性网络）：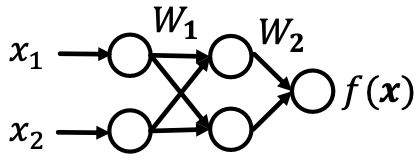
  
  
  ，在一个小批量中计算L2损失。
  隐藏层：输入的中间表示。使用表示隐藏层，。
  ，是一个矩阵（若是二分类则为向量），因此仍然是的线性关系，不论权重矩阵如何构成。
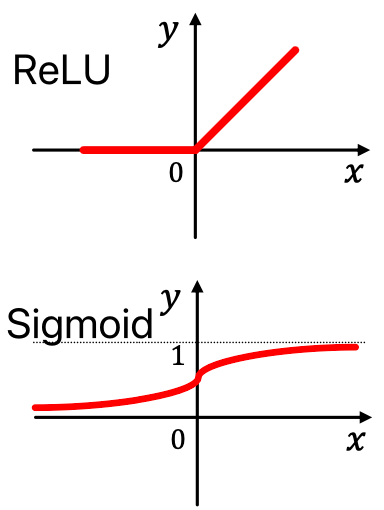
  非线性，如：

• Rectified linear unit (ReLU)：

• Sigmoid：

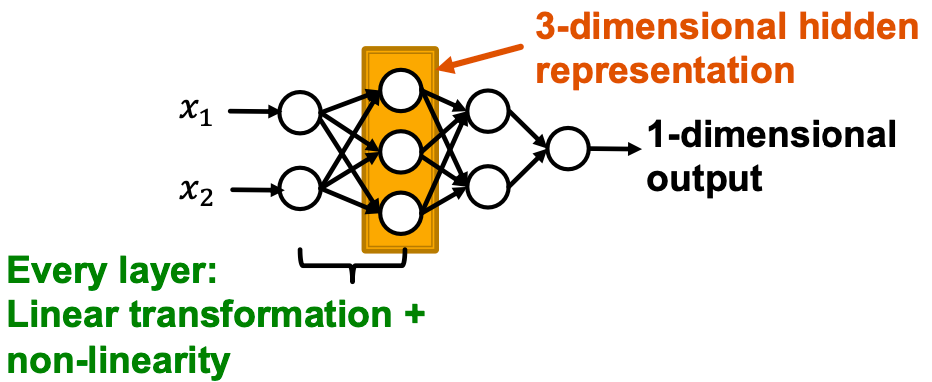
多层感知机 Multi-layer Perceptron MLP

MLP的每一层结合了线性和非线性变换：，其中

• 是将层的隐藏表示转换到层的全值矩阵；
• 是层的bias，添加到的线性变换中；
• 是非线性函数，如sigmoid。

假设是二维的，

Summary

目标函数：

• 可以是简单线性层、MLP或是其他神经网络（如后面将介绍的GNN）
• 抽样输入的一个minibatch
• 向前传播：给定计算
• 反向传播：使用链式法则获取梯度

• 迭代中使用SGD来优化

  Deep Learning for Graphs

  Content：

• 局部网络邻居：

  • 描述聚合策略；
  • 定义计算图
• 叠加(stacking)多层：
  • 描述模型、参数、训练；
  • 如何拟合模型？
  • 无监督和有监督训练的简单例子

假设图：

• 是顶点集
• 是邻接矩阵（假设是binary）
• 是节点特征的矩阵
• 是中的一个节点
• 是的邻居集合

• 节点特征：

  • 社交网络：用户简介、用户形象
  • 生物网络：基因表达谱、基因功能信息
  • 当图数据集中没有节点特征时，指示向量（节点one-hot编码）
  • 常数1的向量为

    A Naive Approach

    连接邻接矩阵和特征，将它们输入到深度神经网络：
    
    这个想法有问题：

• 参数

• 不适用于不同大小的图
• 对节点顺序敏感

Idea：Convolutional Networks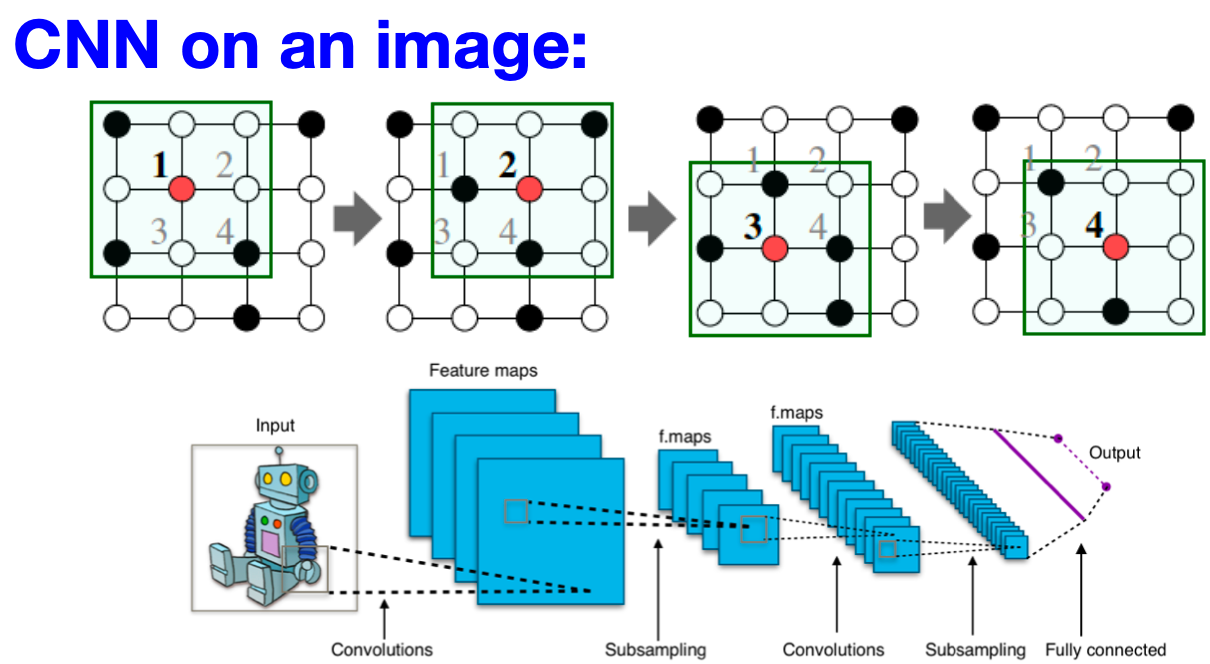

目标是将卷积推广到简单网格数据之外，利用节点特性/属性(如文本、图像)。
但我们的图是这样的：

• 图上没有固定的局部性或滑动窗口的概念
• 图是置换不变的

从图像到图：
filter为的单个CNN层：

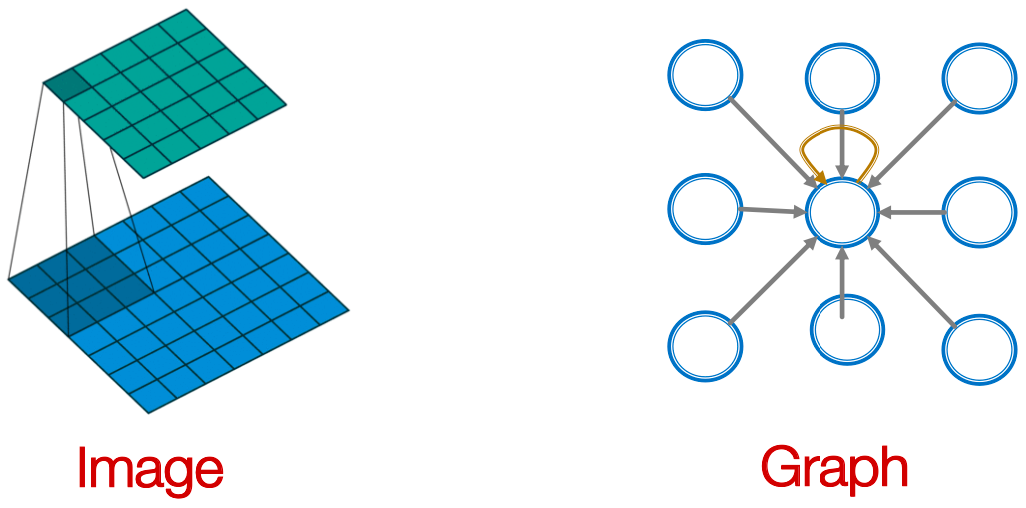
Idea：转换邻居的信息并合并，从邻居转换“消息”，得到，加和为

GNN

Graph Convolutional Networs
Idea：节点的邻域定义了一个计算图

了解如何在图中传播信息以计算节点特征
Key idea：基于局部网络邻域生成节点嵌入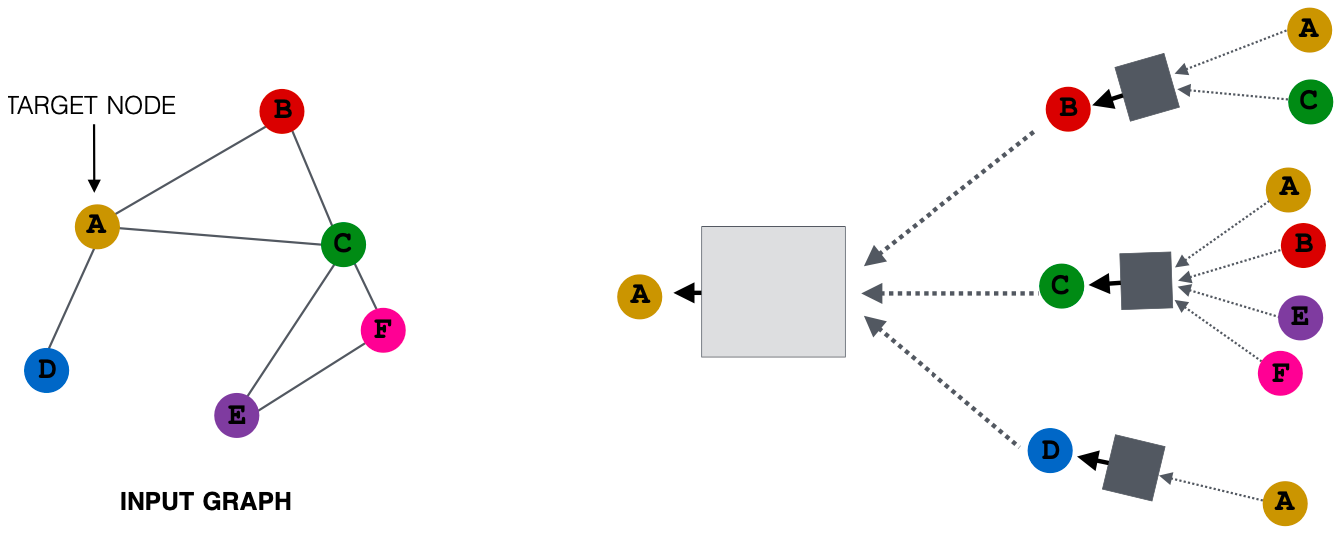

节点聚合的信息来自于使用神经网络的邻居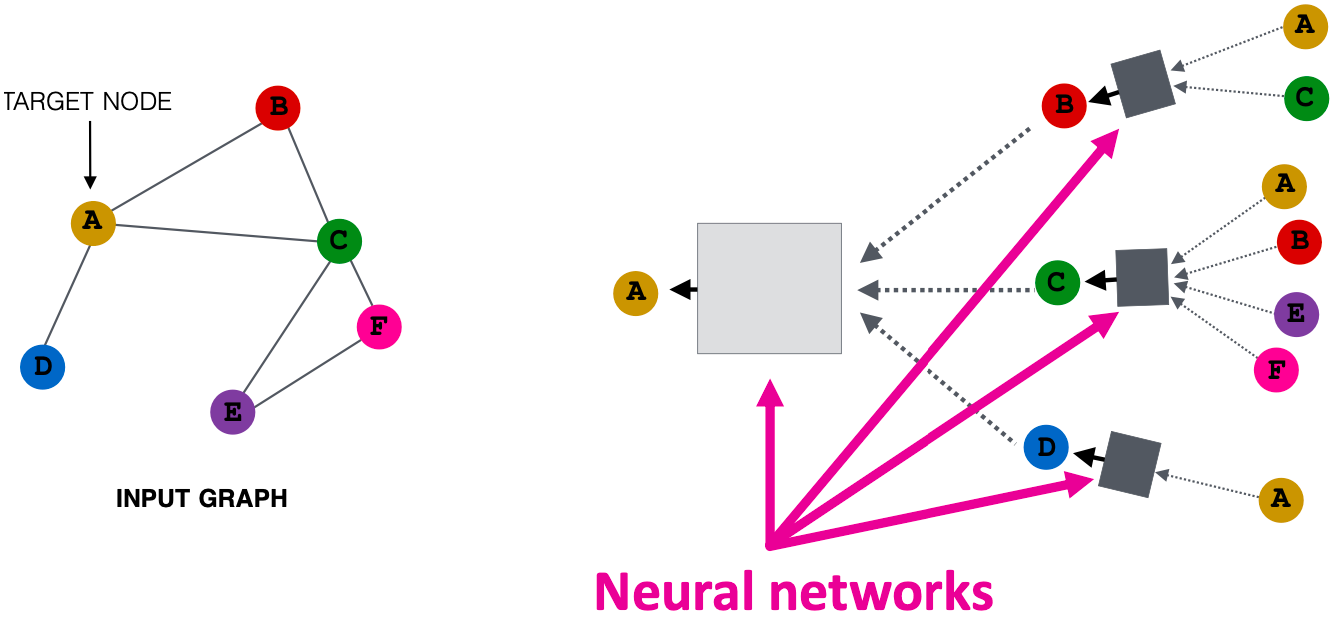

网络邻域定义了一个计算图
每个节点都根据其邻域定义了一个计算图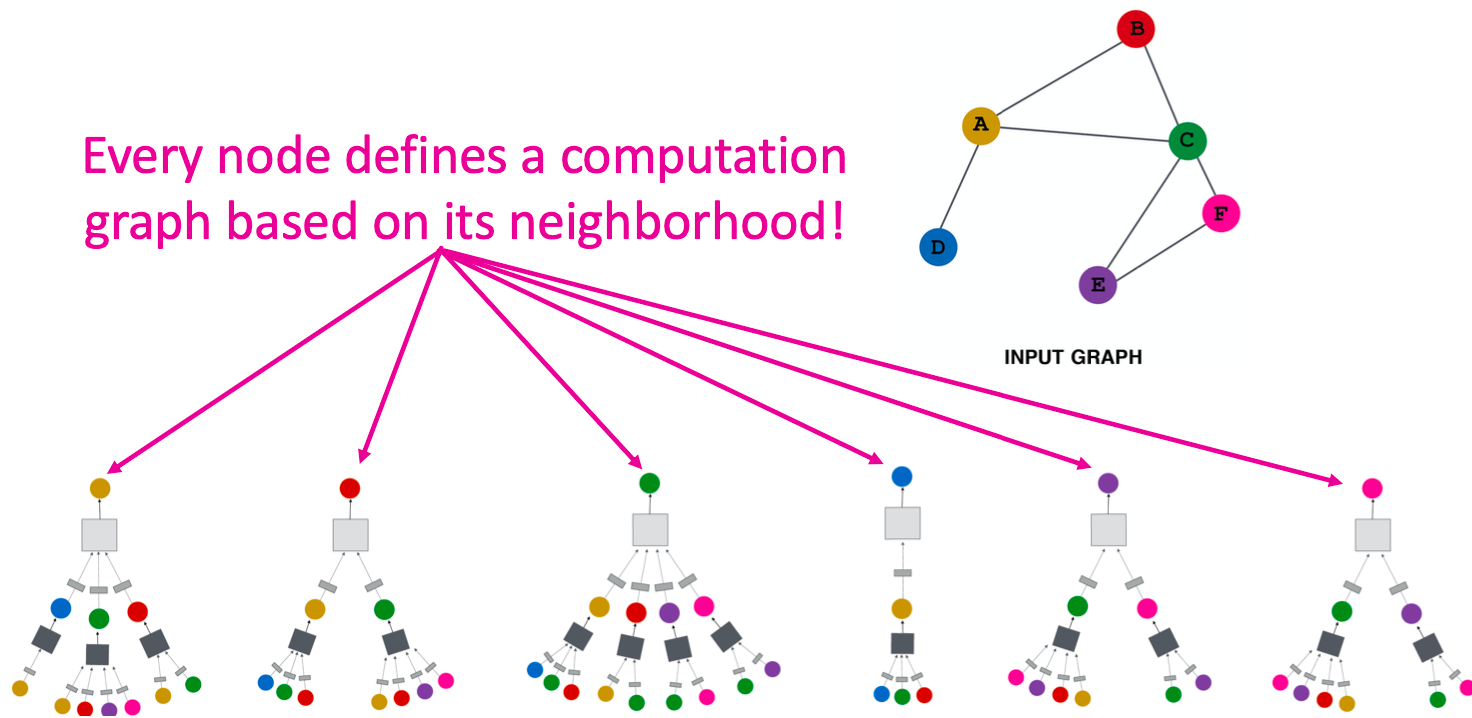

深度模型（多层），可以为任意深度：

• 每层的节点都有嵌入
• 节点的Layer-0嵌入是其输入特征
• Layer-k嵌入从节点中获取信息，这些节点的跳数为

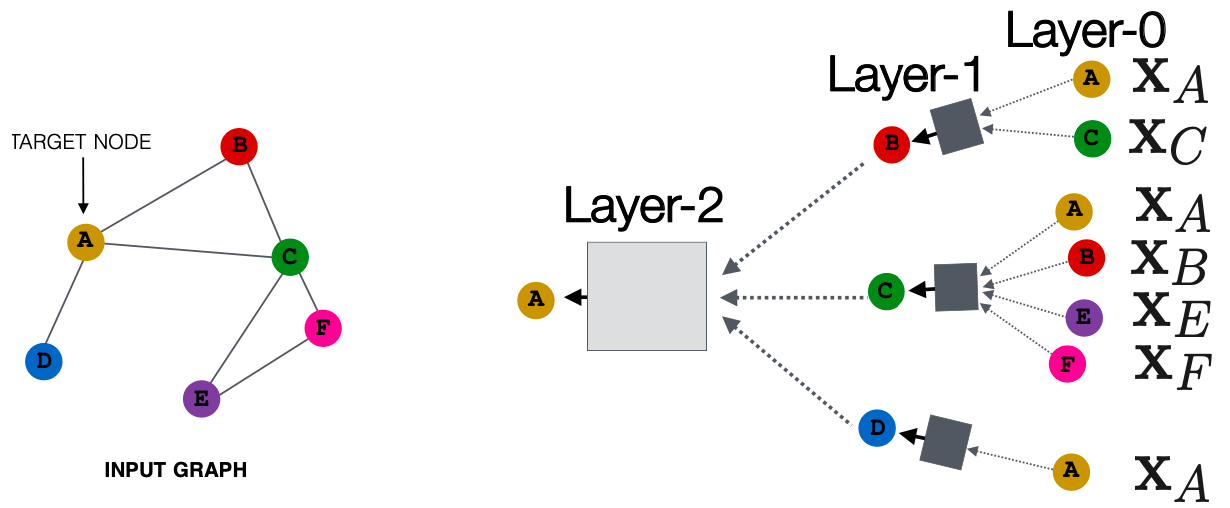
邻域聚合：关键的区别在于不同的方法如何跨层聚合信息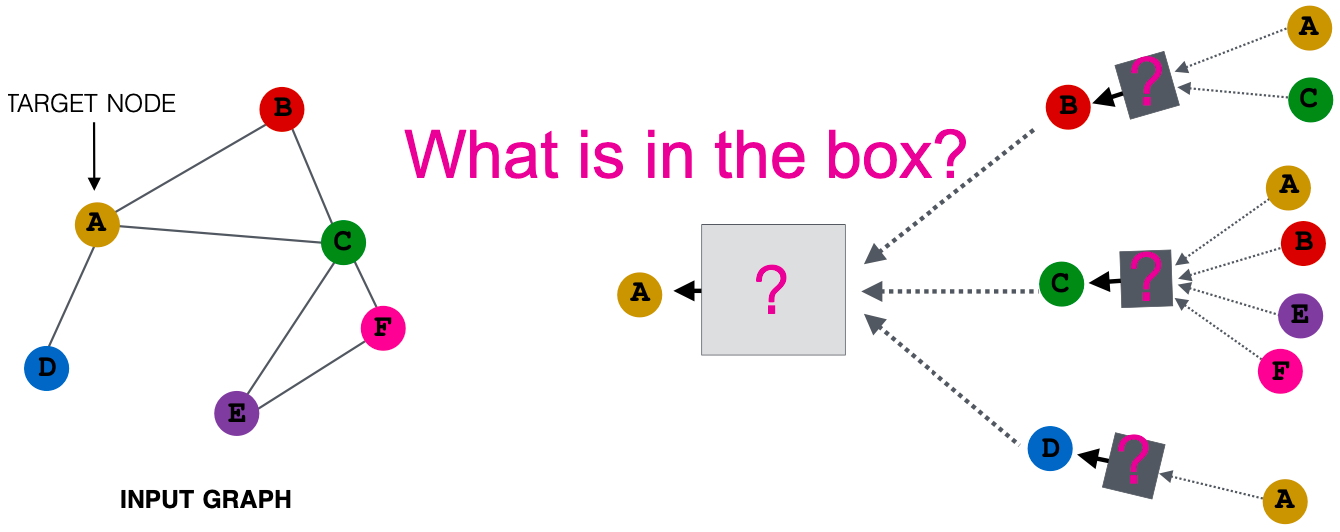

基本方法：平均邻居小心，并应用一个神经网络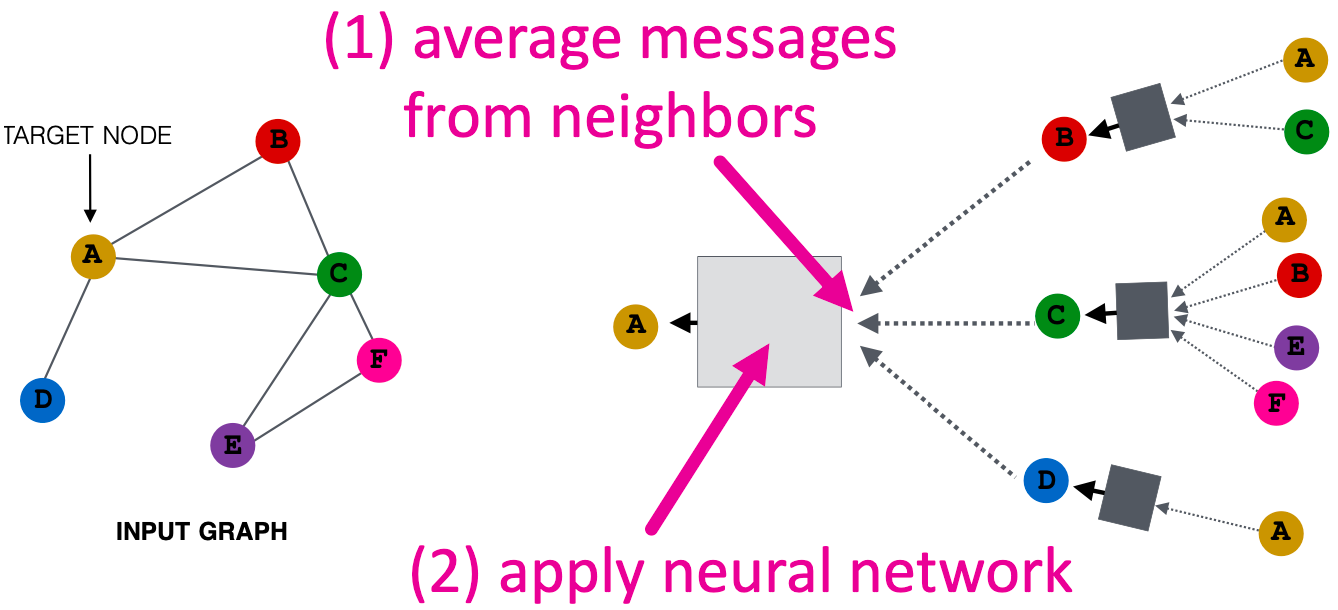

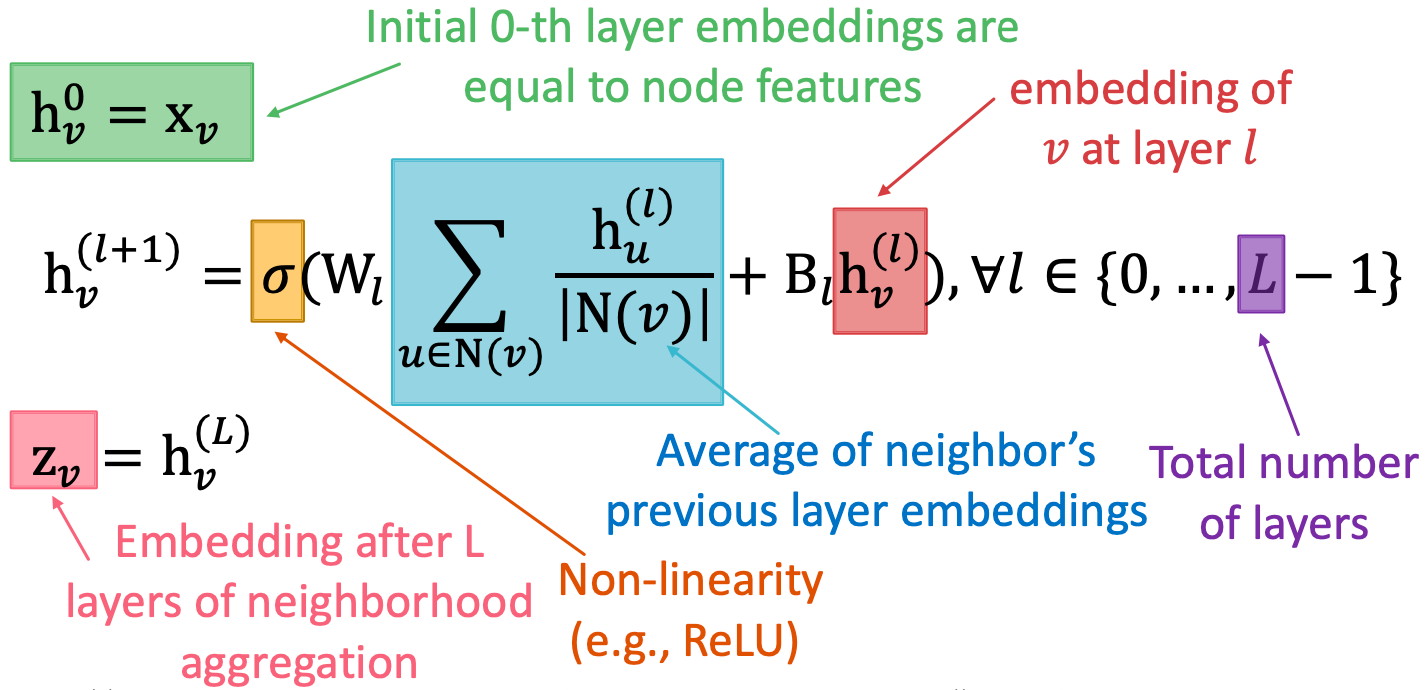
• 可训练的权值矩阵（需要学习得到）
• 最终节点嵌入
• 在层的节点的隐藏表示
• 邻域聚合的权值矩阵
• 变换自身隐藏向量的权值矩阵

我们可以将这些嵌入代入到任何损失函数中，并运行SGD来训练权重参数。
许多聚合可以通过(稀疏)矩阵操作有效地执行，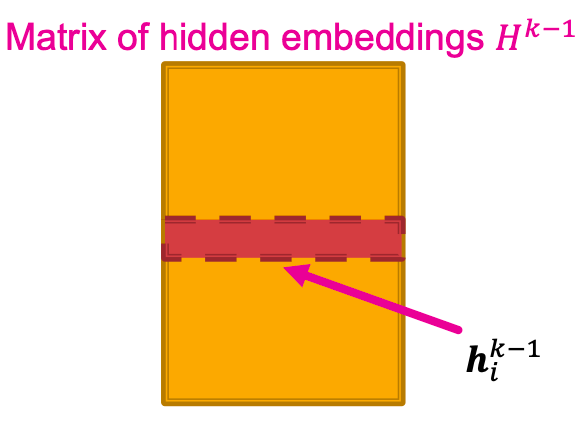

• 设，则有
• 设为对角阵，，
• 由此，

在实践中，这意味着可以使用高效的稀疏矩阵乘法（是稀疏的）。
注：当聚合函数比较复杂时，并不是所有的GNN都可以用矩阵形式表示。

训练模型

节点嵌入是输入图的一个函数，
有监督：极小化损失函数，即

• 节点标签
• 可以是L2当是真的数字时，或cross entropy当是类别时

无监督：

• 不需要节点标签

• 使用图结构作为监督

  无监督训练

  “相似”节点有相似的嵌入：

• 当和相似时，

• CE 是cross entropy
• DEC 是解码器，如内积

节点相似度可以是lecture3中的任何东西，例如，基于以下内容的损失：

• Random walks (node2vec, DeepWalk, struc2vec)
• Matrix factorization
• Node proximity in the graph

  有监督训练

  直接训练模型执行有监督的任务(例如，节点分类)，使用cross entropy损失：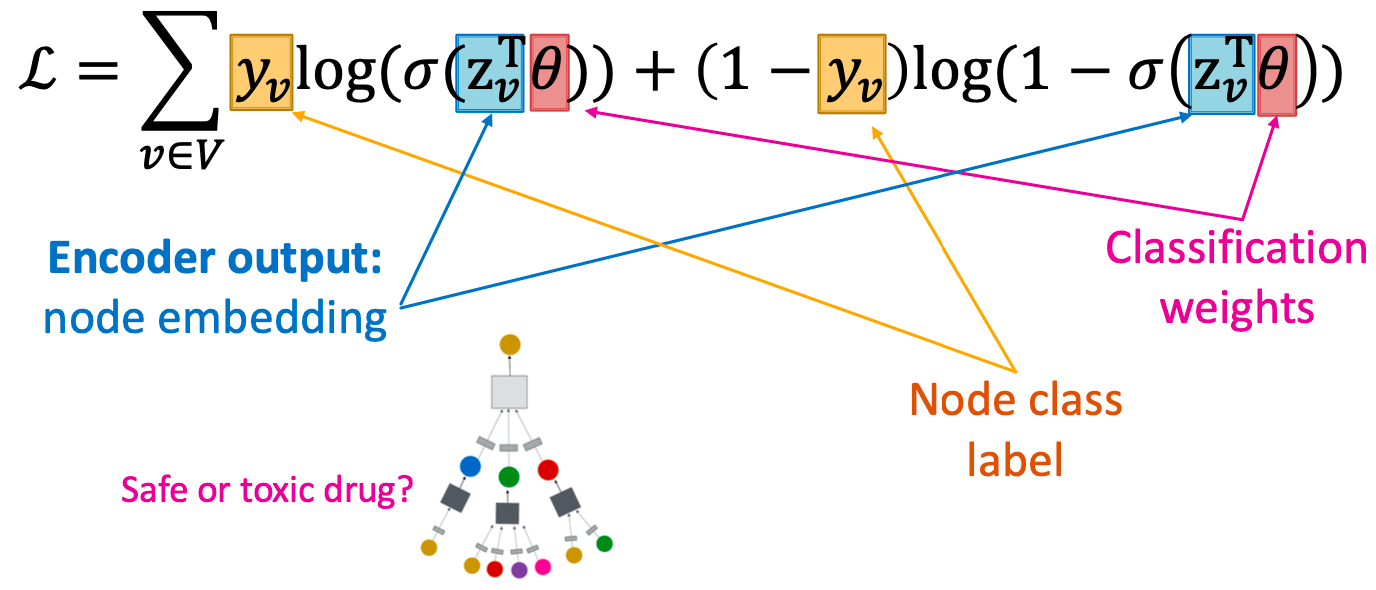
  

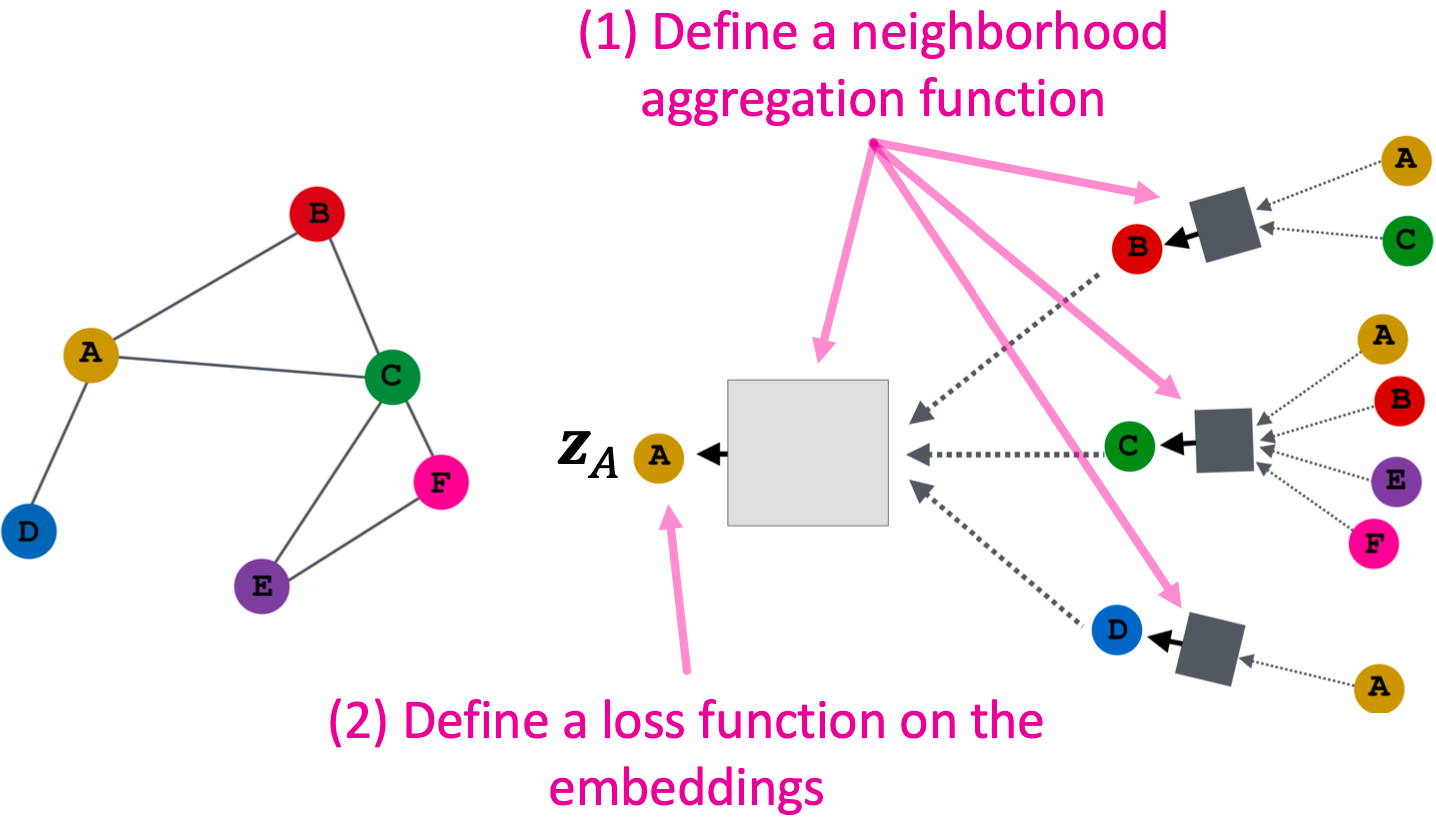
  模型设计概述

1. 定义邻域聚合函数
2. 基于嵌入定义损失函数
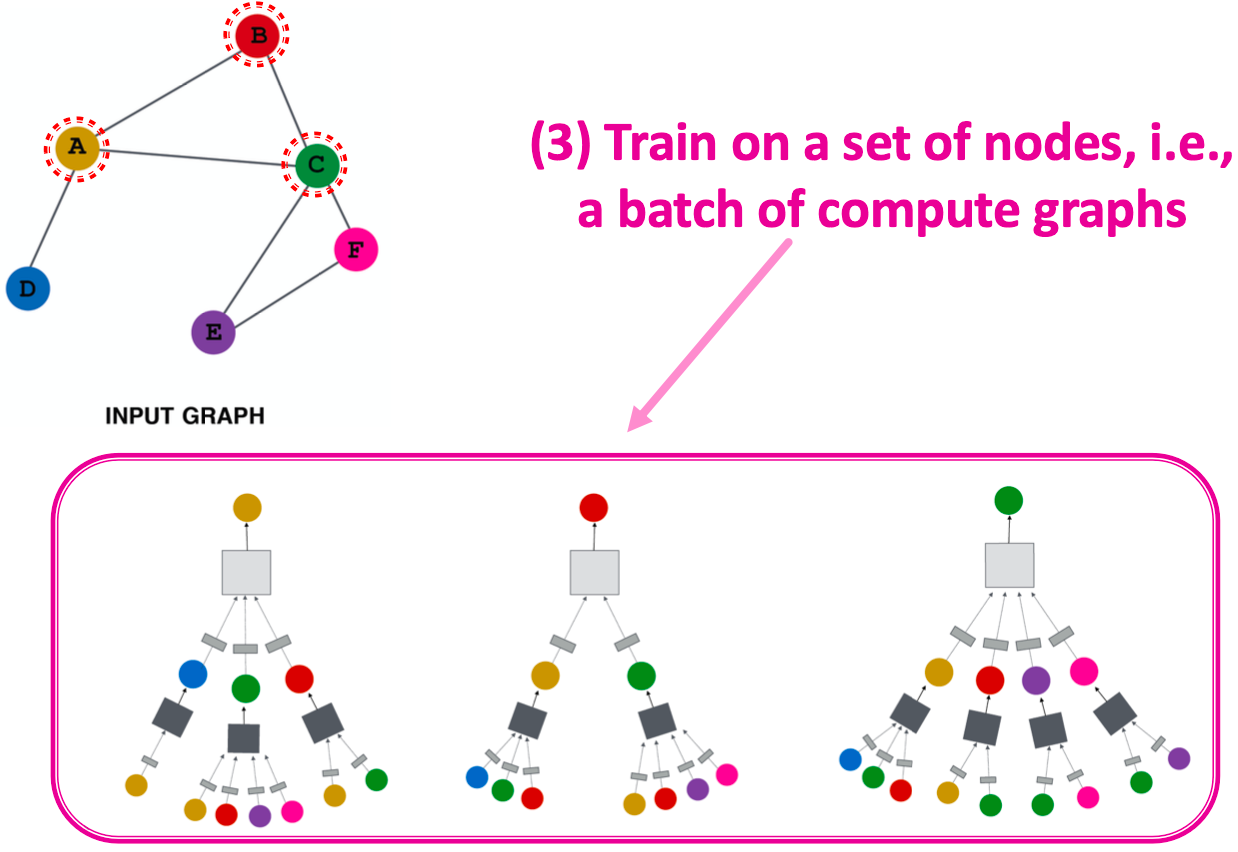
3. 在一组节点上训练，即一批计算图
4. 根据需要为节点生成嵌入

归纳能力

所有节点共享相同的聚合参数，在中，模型参数的数量是次线性的，我们可以推广到看不见的节点!

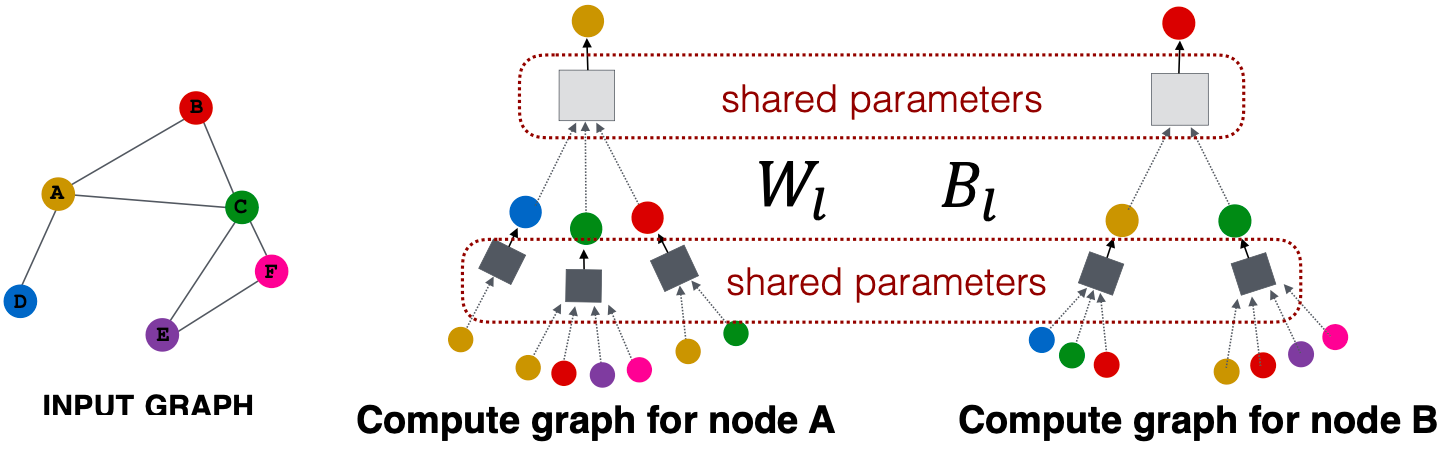
Inductive Capability: New Graphs

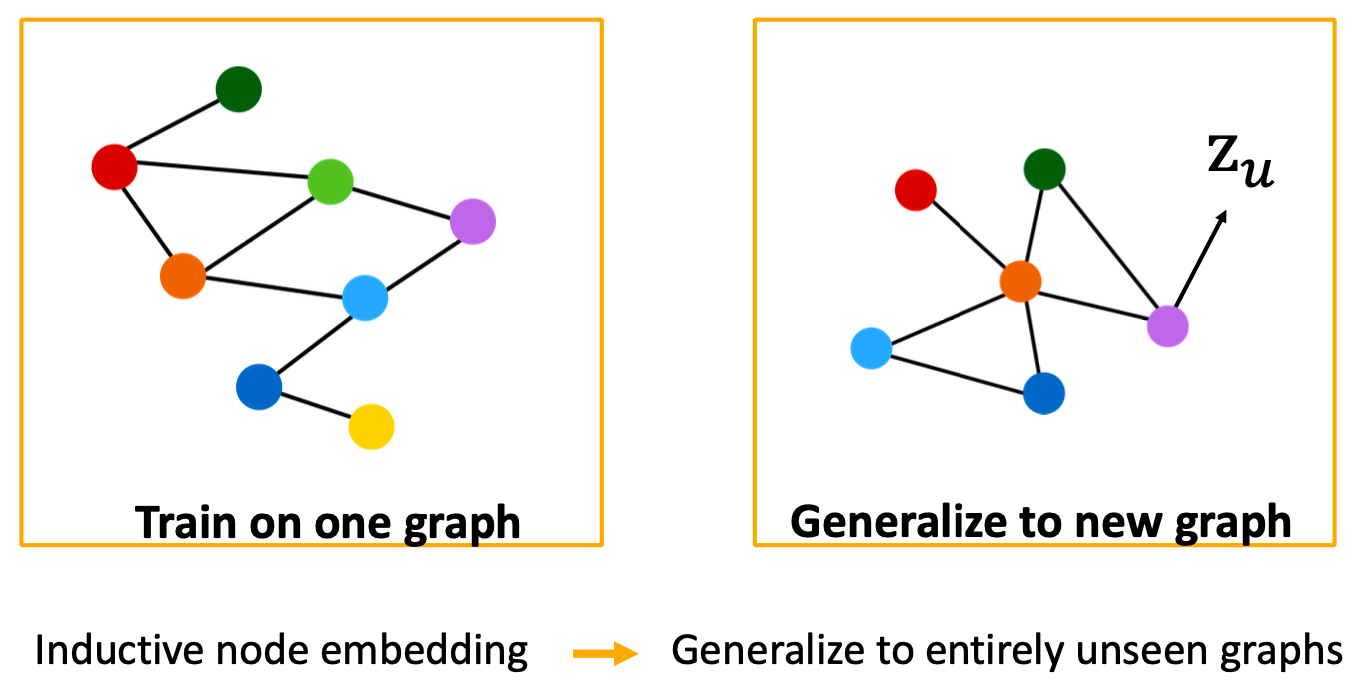
例如，对模型生物A的蛋白质相互作用图进行训练，并对新收集的关于生物B的数据进行嵌入。

Inductive Capability: New Nodes

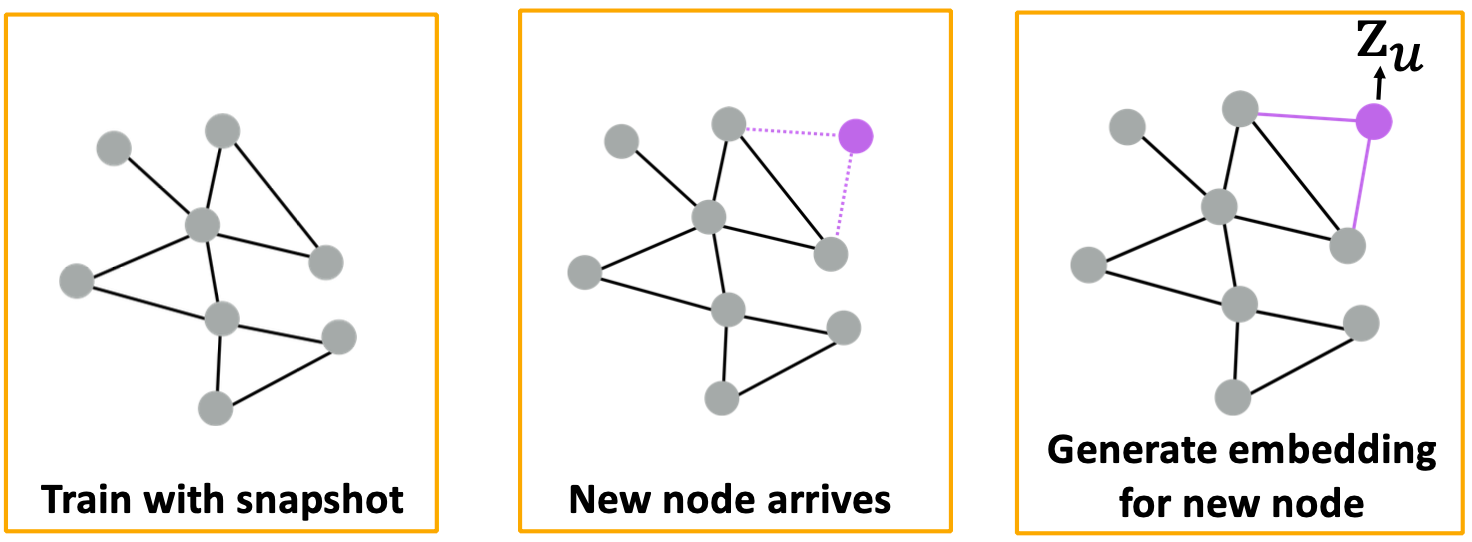
许多应用程序设置经常遇到以前未见过的节点，如Reddit、YouTube、谷歌Scholar等，需要生成新的嵌入“on the fly”。

Summary

通过聚合邻域信息来生成节点嵌入，我们看到了这个观点的一个基本变体，主要的区别在于不同的方法如何跨层聚合信息。接下来，描述GraphSAGE图神经网络的结构。

Graph Convolutional Networks and GraphSAGE

到目前为止，我们已经通过计算邻居消息的(加权)平均值来聚合它们，我们能做得更好吗?
GraphSAGE思想：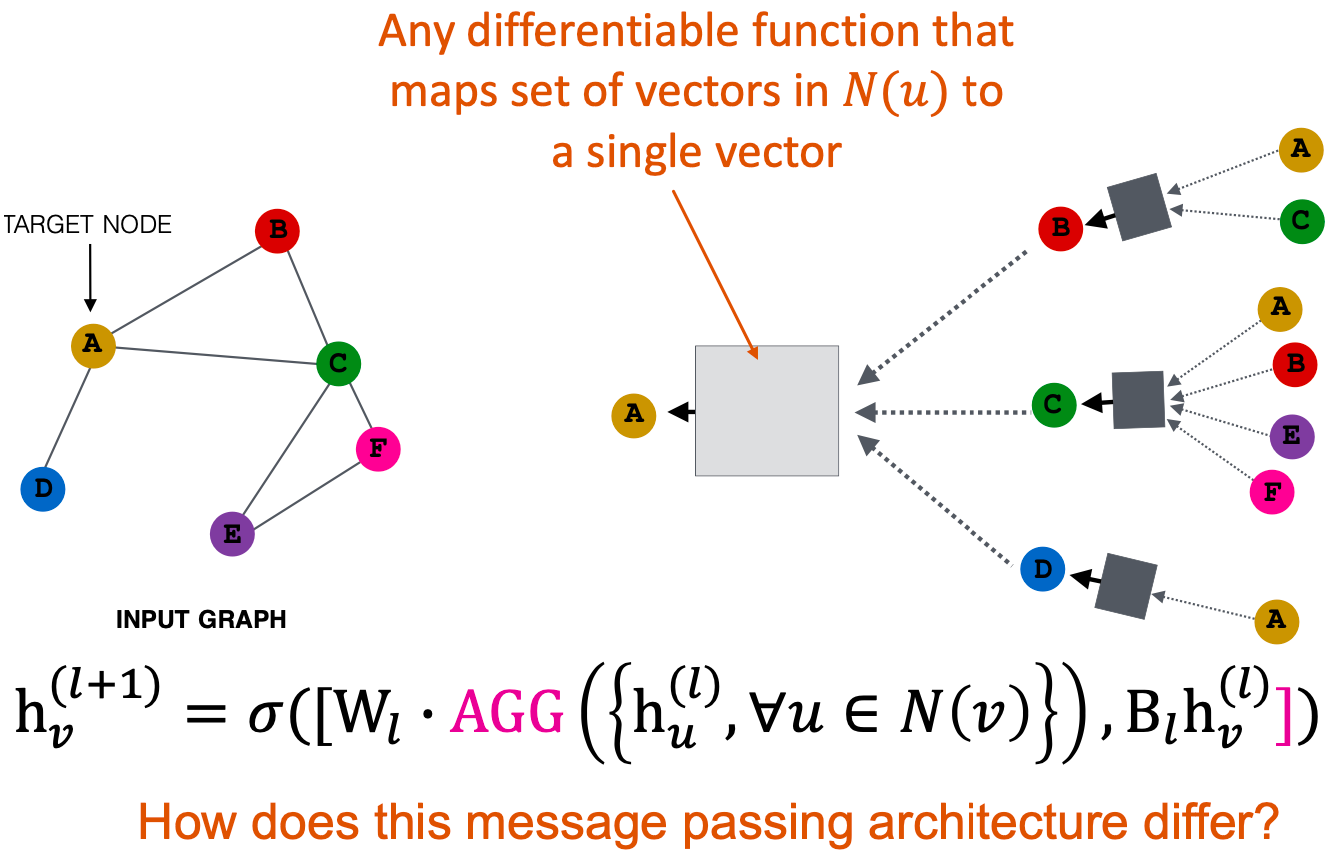

可选：对每一层的嵌入应用L2规范化。
L2 normalization：

• 
• 没有范化时，向量的嵌入具有不同的尺度(范数)
• 在某些情况下(并非总是如此)，嵌入的规范化可以提高性能
• 范化后，所有向量都有同样的范数

简单的邻域聚合：

GraphSAGE：

邻居聚合的变体：

• Mean：取邻居的加权平均，
• Pool：变换邻居向量，应用对称向量函数，

• LSTM：对重组后的邻居应用LSTM，

  Recap: GCN, GraphSAGE

• Key idea：基于局部邻域生成节点嵌入，节点使用神经网络从它们的邻居聚合“信息”。

• Graph convolutional networks：基本变体是平均邻域信息和stack神经网络；

• GraphSAGE：广义化邻域聚合。

  Summary

• Basics of neural networks：损失、优化、梯度、SGD、非线性、MLP。

• Idea for Deep Learning for Graphs：多层嵌入转换；在每一层，使用前一层的嵌入作为输入；邻居的聚合和自我嵌入。
• Graph Convolutional Network：平均聚合；可以用矩阵形式表示。
• GraphSAGE：更灵活的聚合。