三个基本步骤

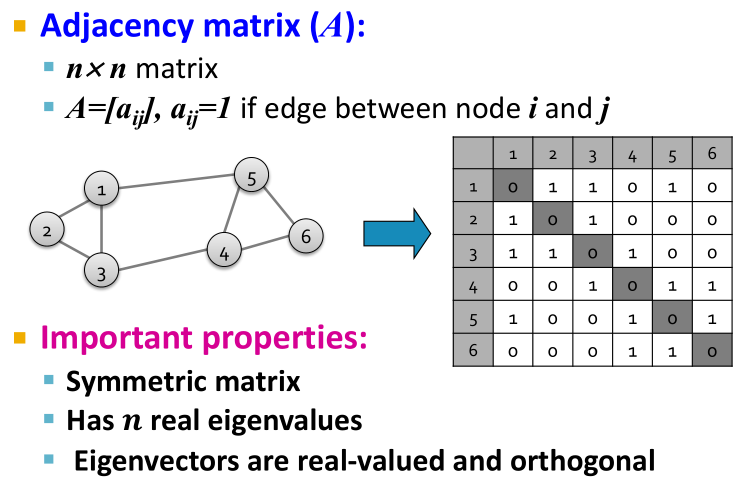
1、Pre-processing：用矩阵表示图；
2、Decomposition：计算矩阵的特征值-特征向量；基于一个或多个特征向量，将每个点映射为低维表示；
3、Grouping：基于新的表示，将点分配到两个或多个clusters。

Graph partition

一个好的划分：

  • 极大化组内连接的数量；
  • 极小化组间连接的数量。

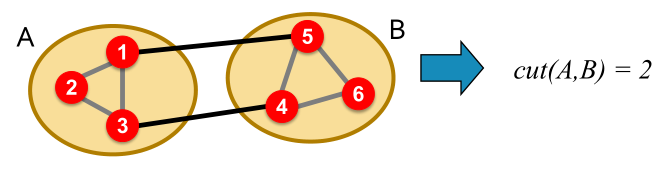
image.png

Graph Cuts

Cut：每组有一个端点的边的集合。
05 Spectral Clustering - 图2
若图是被加权的，则05 Spectral Clustering - 图3是权值；否则05 Spectral Clustering - 图4。
image.png

Graph Cut Crterion

criterion 标准，准则：Minimum-cut 极小化组间连接的权重 05 Spectral Clustering - 图6
degenerate（质量）下降；退化，衰退 case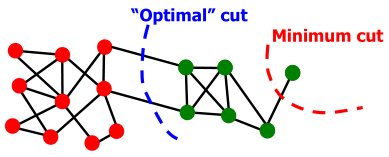：image.png
问题：（1）仅考虑外部簇的连接；（2）没有考虑内在簇的连接性。

Criterion：Conductance 电导（率）；（热）传导性 【Shi-Malik，97】
组间连接性与每个组间的密度有关：05 Spectral Clustering - 图8
05 Spectral Clustering - 图9 节点在A中总加权度，05 Spectral Clustering - 图10 A中边缘端点的个数
conductance准则能划分更加平衡些。计算最好的conductance cut是NP-hard问题。

Spectral Graph Partitioning

05 Spectral Clustering - 图11是无向图05 Spectral Clustering - 图12的邻接矩阵，05 Spectral Clustering - 图13
05 Spectral Clustering - 图14是一个向量，想象05 Spectral Clustering - 图15是05 Spectral Clustering - 图16的每个节点上的标签/值。
05 Spectral Clustering - 图17，即05 Spectral Clustering - 图18是05 Spectral Clustering - 图19的邻居标签05 Spectral Clustering - 图20的总和

Spectral Graph Theory

spectrum 光谱；波谱；声谱；频谱；序列
spectrum：一个图的特征向量05 Spectral Clustering - 图21按照对应的特征值大小排序05 Spectral Clustering - 图22

Example:d-Regular Graph

  1. 设05 Spectral Clustering - 图23中所有节点的度均为05 Spectral Clustering - 图24（05 Spectral Clustering - 图25是d-regular）且05 Spectral Clustering - 图26是连接的。

05 Spectral Clustering - 图27
05 Spectral Clustering - 图28
05 Spectral Clustering - 图29是05 Spectral Clustering - 图30最大的特征值

  1. 设05 Spectral Clustering - 图31不是连接的，05 Spectral Clustering - 图32有2部分，每个都是d-regular。

image.png
orthogonal 直角的，正交的，垂直的
image.png

Adjacency Matrix A

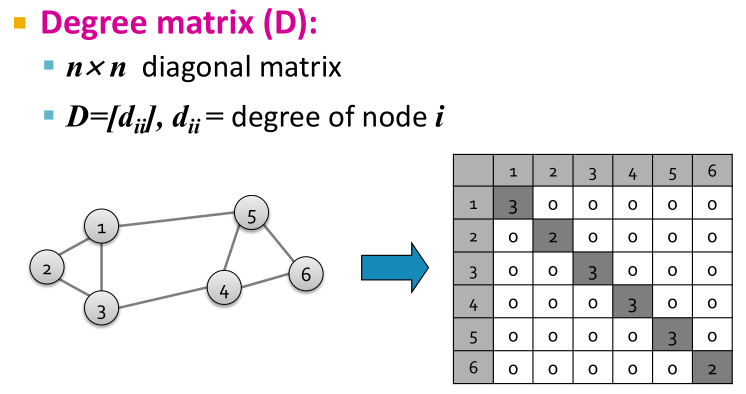
image.png

Degree Matrix D

image.png

Laplacian Matrix L

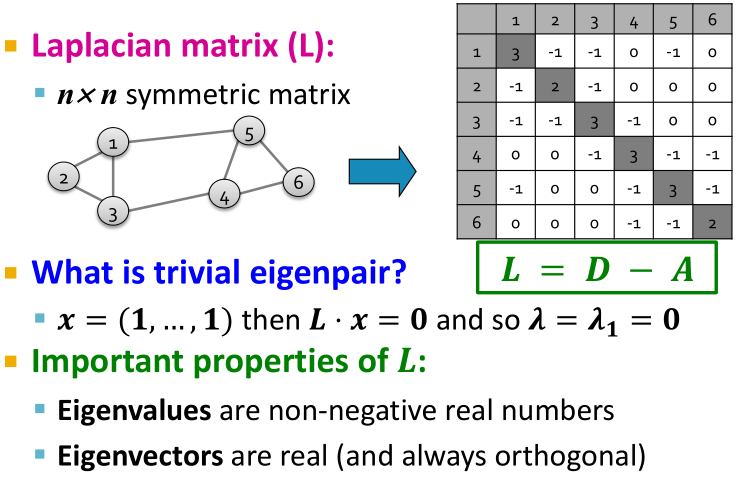
image.png
trivial 不重要的；琐碎的；微不足道的
Laplacian L 的三个性质：

  • (a) 所有的特征值都大于等于零；
  • (b) 对每个05 Spectral Clustering - 图38，有05 Spectral Clustering - 图39;
  • (c) 05 Spectral Clustering - 图40可以写成05 Spectral Clustering - 图41，即05 Spectral Clustering - 图42是半正定的。

证明：

  • (c) -> (b) 05 Spectral Clustering - 图43
  • (b) -> (a) 设05 Spectral Clustering - 图44为05 Spectral Clustering - 图45的特征值，又 (b) 05 Spectral Clustering - 图46，所以05 Spectral Clustering - 图47
  • (a) -> (c)

05 Spectral Clustering - 图48
由于05 Spectral Clustering - 图49，当05 Spectral Clustering - 图50时，05 Spectral Clustering - 图51，则05 Spectral Clustering - 图52为拉普拉斯矩阵的一个特征值。又由于拉普拉斯矩阵的特征值非负，所以0为最小的特征值，对应的特征向量为05 Spectral Clustering - 图53

由于节点05 Spectral Clustering - 图54的度为05 Spectral Clustering - 图55，所以值05 Spectral Clustering - 图56需要被加和05 Spectral Clustering - 图57次。但每个边05 Spectral Clustering - 图58有两个端点，所以需要05 Spectral Clustering - 图59，即05 Spectral Clustering - 图60 。

第二小特征值的意义

结论：任意对称矩阵M，有05 Spectral Clustering - 图61，其中05 Spectral Clustering - 图62是矩阵M第一小特征值05 Spectral Clustering - 图63对应的特征向量，05 Spectral Clustering - 图64是矩阵M的第二小特征值。
证明：设05 Spectral Clustering - 图65为矩阵M的特征值-特征向量,即05 Spectral Clustering - 图66。
设05 Spectral Clustering - 图67，则05 Spectral Clustering - 图68，即05 Spectral Clustering - 图69，则有05 Spectral Clustering - 图70。
当05 Spectral Clustering - 图71时，05 Spectral Clustering - 图72，则05 Spectral Clustering - 图73。

特征值&谱聚类

两个结论：
05 Spectral Clustering - 图74
05 Spectral Clustering - 图75
为了满足上述两式，需要两个限制条件：

  • 05 Spectral Clustering - 图76是一个单位向量，05 Spectral Clustering - 图77
  • 05 Spectral Clustering - 图78，由于在拉普拉斯矩阵中，最小特征值为0，对应的特征向量为05 Spectral Clustering - 图79，则05 Spectral Clustering - 图80

由于05 Spectral Clustering - 图81，则05 Spectral Clustering - 图82必然有正有负，如下图所示，在坐标轴两侧有些点。在谱聚类中，希望最大化组内连接数，最小化组间连接数，即希望有尽可能少的点跨越0点，从数学表达式中看，希望05 Spectral Clustering - 图83。联合上式，有05 Spectral Clustering - 图84。
为什么不是利用05 Spectral Clustering - 图85呢？因为05 Spectral Clustering - 图86恒为0，此时图一定是不连通的，最小化没有意义，所以要给一个限制条件后利用第二小的特征值。
终上所述，就可以利用拉普拉斯矩阵的第二小特征值对应的特征向量来进行划分。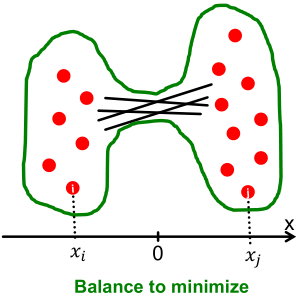
image.png

提到的其他问题：
可证明，若将图G划分为A和B两个部分，且05 Spectral Clustering - 图88，则对于评价指标conductance 05 Spectral Clustering - 图89，有05 Spectral Clustering - 图90，即找到的这种划分标准是conductance的下界。
证明：设05 Spectral Clustering - 图91，05 Spectral Clustering - 图92
则有05 Spectral Clustering - 图93
05 Spectral Clustering - 图94

05 Spectral Clustering - 图95，其中05 Spectral Clustering - 图96表示节点度的最大值。

上述方法是划分两类，如何划分为05 Spectral Clustering - 图97类呢？

  • Recursive bi-partitioning递归利用二分算法，将图划分为多类；
  • 聚类多个特征向量，选择05 Spectral Clustering - 图98个特征向量，对这05 Spectral Clustering - 图99个特征向量利用聚类方法（如k-means）将其聚为05 Spectral Clustering - 图100类。

为什么使用多个特征向量？

  • 近似于最优切割
  • 强调凝聚力集群：（1）增加了数据分布的不均匀性；（2）相似点之间的联系被放大，不同点之间的关联减弱；（3）数据开始“近似聚类”
  • Well-separated space：将数据转换为一个由k个正交基向量组成的新的“嵌入式空间”
  • 多重特征向量可以防止由于信息丢失而导致的不稳定性

如何选择k？
Eigengap：两个连续特征值之间的差。最稳定的聚类通常由最大eigengap的05 Spectral Clustering - 图101值给出，05 Spectral Clustering - 图102（特征值降序排列）
如：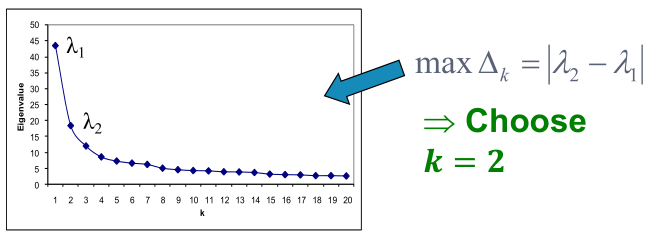
image.png

补充：

  • 若05 Spectral Clustering - 图104是一个05 Spectral Clustering - 图105矩阵，则05 Spectral Clustering - 图106的转置记为05 Spectral Clustering - 图107，05 Spectral Clustering - 图108；矩阵05 Spectral Clustering - 图109的复数共轭05 Spectral Clustering - 图110仍然是一个05 Spectral Clustering - 图111矩阵，其元素定义为05 Spectral Clustering - 图112；矩阵05 Spectral Clustering - 图113的（复）共轭转置记为05 Spectral Clustering - 图114，它是一个05 Spectral Clustering - 图115矩阵，共轭转置又叫Hermitian伴随、Hermitian转置或Hermitian共轭。
  • 对称矩阵：满足05 Spectral Clustering - 图116的正方实矩阵。
  • Hermitian矩阵（复共轭对称矩阵）：满足05 Spectral Clustering - 图117的正方复矩阵。05 Spectral Clustering - 图118
  • 对一个实值矩阵，Hermitian矩阵与对称矩阵等价。
  • 实对称矩阵、Hermitian矩阵的所有特征值都是实数。
  • 若一个05 Spectral Clustering - 图119的矩阵05 Spectral Clustering - 图120是奇异的，则它至少有一个特征值为0；若矩阵是非奇异的，则它所有的特征值非零。
  • Hermitian矩阵05 Spectral Clustering - 图121的Rayleigh商或Rayleigh-Ritz比05 Spectral Clustering - 图122是一个标量，定义为05 Spectral Clustering - 图123，其中05 Spectral Clustering - 图124是待选择的向量，其目的是使Rayleigh商最大化或最小化。

  • Rayleigh-Ritz定理：Hermitian矩阵05 Spectral Clustering - 图125的特征值为05 Spectral Clustering - 图126，若05 Spectral Clustering - 图127，则05 Spectral Clustering - 图128；若05 Spectral Clustering - 图129，则05 Spectral Clustering - 图130。

    寻找最优切分点

    image.png

    Rayleigh Theorem

    05 Spectral Clustering - 图132
    05 Spectral Clustering - 图133

  • 05 Spectral Clustering - 图134：05 Spectral Clustering - 图135的最小值是拉普拉斯矩阵05 Spectral Clustering - 图136的第二小特征值05 Spectral Clustering - 图137

  • 05 Spectral Clustering - 图138：05 Spectral Clustering - 图139的最优解由05 Spectral Clustering - 图140对应的特征向量05 Spectral Clustering - 图141给出，称为Fiedler向量
  • 可以使用05 Spectral Clustering - 图142的符号来决定将节点05 Spectral Clustering - 图143分到哪一类别中

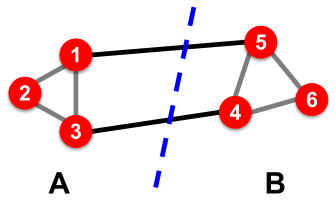
Spectral Clusstering Algorithm

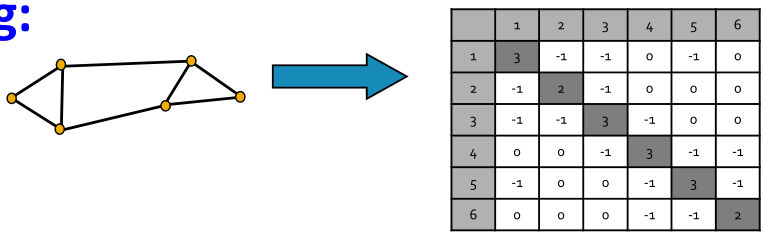
三个基本步骤：

  1. 预处理：利用图的邻接矩阵05 Spectral Clustering - 图144，度矩阵05 Spectral Clustering - 图145，计算拉普拉斯矩阵05 Spectral Clustering - 图146；

image.png

  1. 分解decomposition：计算拉普拉斯矩阵05 Spectral Clustering - 图148的特征值-特征向量，其中第二小特征值05 Spectral Clustering - 图149对应的特征向量为05 Spectral Clustering - 图150；

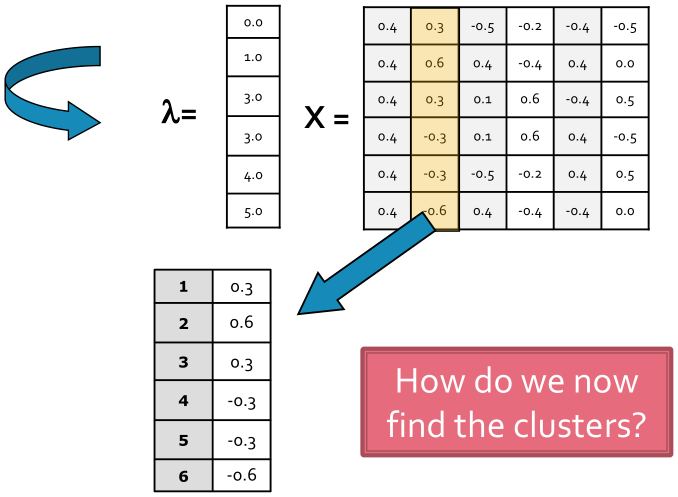
image.png

  1. 分类grouping：对上述的特征向量05 Spectral Clustering - 图152进行分组，如可以利用正负或中位数进行划分。如下图所示，节点123特征向量为正，划分为一组；节点456特征向量为负，划分为一组。

image.png

基于motif的谱聚类

Small subgraphs (motifs, graphlets) are building blocks of networks. 将图拆解为一个个子图来重新看待网络，motif给了网络一个新的定义方式，可考虑从motif（而不是边）的角度进行谱聚类。

motif conductance

类比edge cut和conductance，针对motif可以如下定义：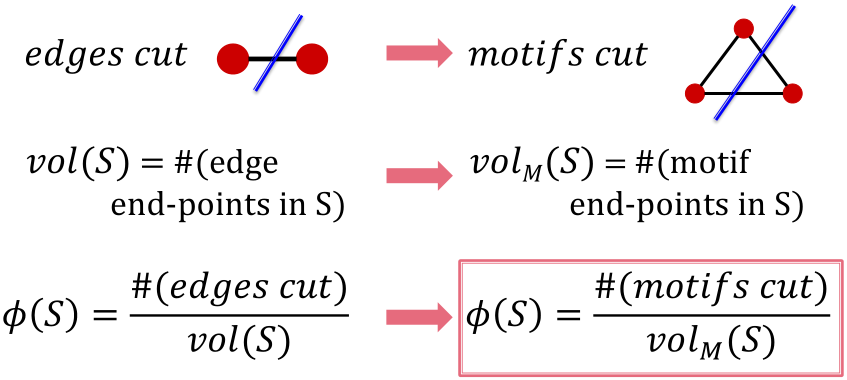
image.png
给定一个motif M和一个图G，找到使得motif conductance最小的节点集合S，这是一个NP-hard问题。
motif conductance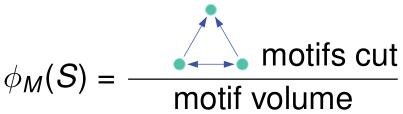：image.png
解决方法：motif spectral clustering

  • 输入：图G和motif M；
  • 将G表示成一个新的带权重的图05 Spectral Clustering - 图156；
  • 在图05 Spectral Clustering - 图157上进行谱聚类；
  • 输出聚类结果。

优化motif conductance

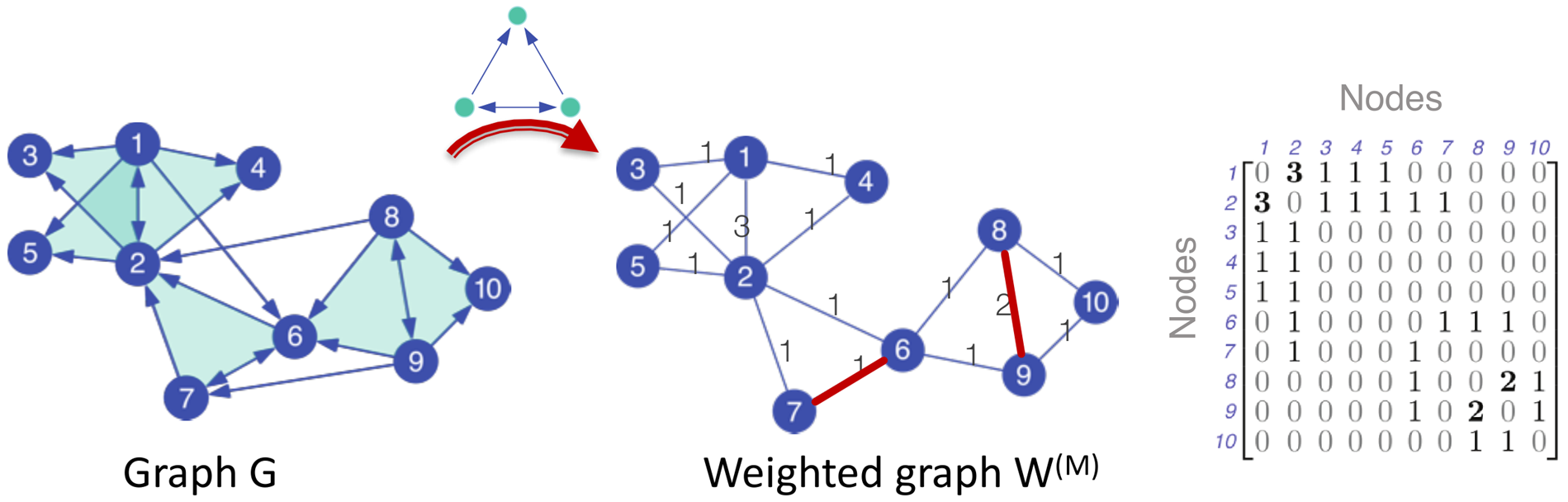
  1. 预处理：05 Spectral Clustering - 图158微信截图_4.png
  2. 分解：基于05 Spectral Clustering - 图160使用标准的谱聚类，计算拉普拉斯矩阵05 Spectral Clustering - 图161的第二小特征值对应的特征向量（又称为Fiedler向量）05 Spectral Clustering - 图162。具体地，计算05 Spectral Clustering - 图163，根据05 Spectral Clustering - 图164求出05 Spectral Clustering - 图165。
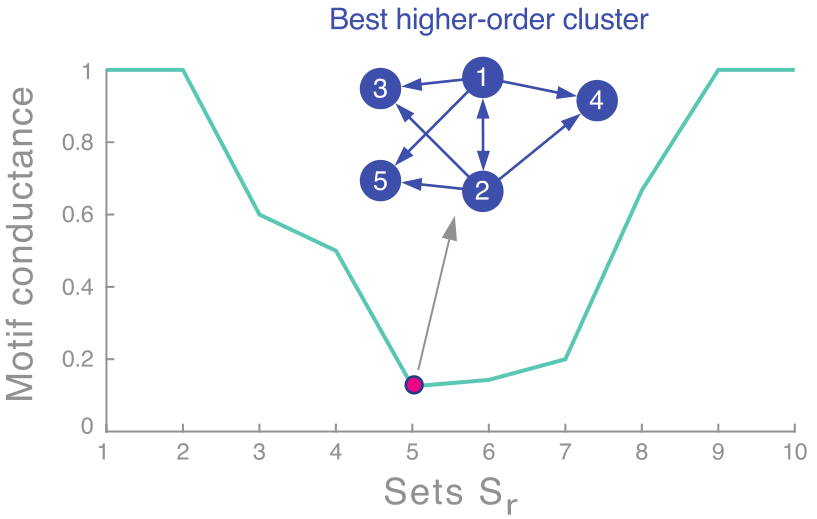
  3. 分组（sweep procedure）：将第二小特征值对应的特征向量05 Spectral Clustering - 图166中的每个元素按照取值大小排序，得到：05 Spectral Clustering - 图167。设05 Spectral Clustering - 图168，计算每个05 Spectral Clustering - 图169的motif conductance。如下图所示，当05 Spectral Clustering - 图170时取得最小的motif conductance。

image.png
Motif Cheeger Inequality：05 Spectral Clustering - 图172，其中05 Spectral Clustering - 图173表示我们的算法找到的节点集合S的motif conductance，05 Spectral Clustering - 图174表示最优集合05 Spectral Clustering - 图175的motif conductance。由此可知，我们算法找到的S是近似于最优解的。

例子

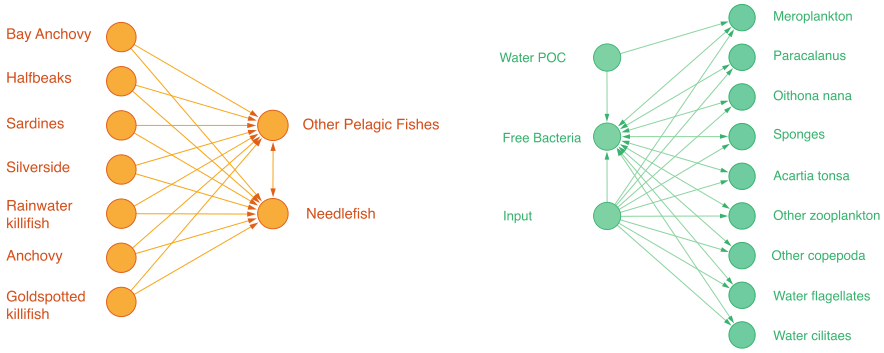
应用1 食物链

佛罗里达湾食物链：节点是在生态系统的物种，边是碳交换(谁吃谁)。
不同的motifs捕捉到不同的能量流动模式，从下图中可看出motif M6取到最小的conductance值，因此该食物链由motif M6构成。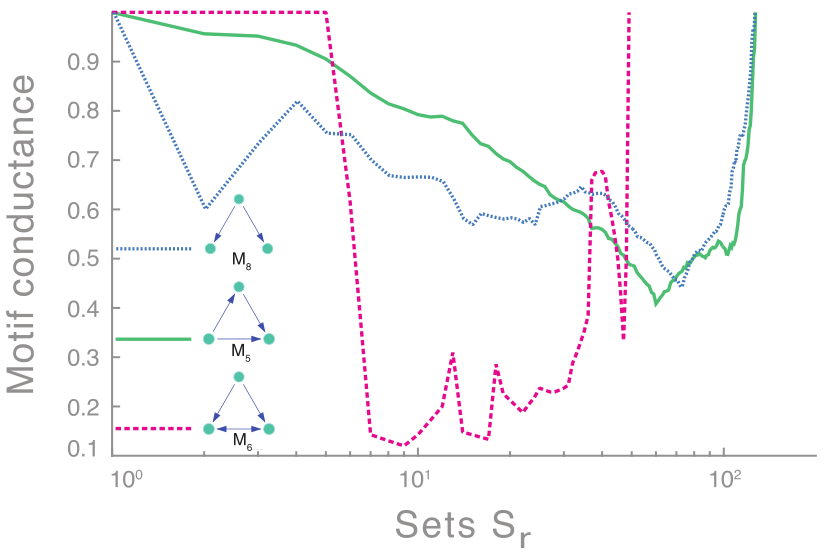
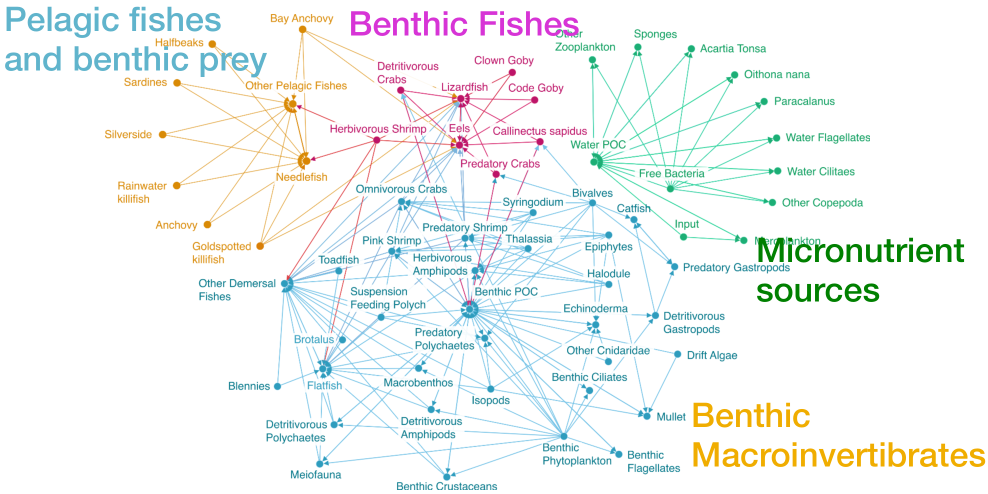
image.png
image.png
M6以更高的精度揭示了已知的水生生物层(84% vs. 65%)。

水生生物层的结构（基于motif M6）：image.png

应用2 基因调控网络

Nodes are groups of gene in mRNA. Edges are directed transcriptional regulation relationships.
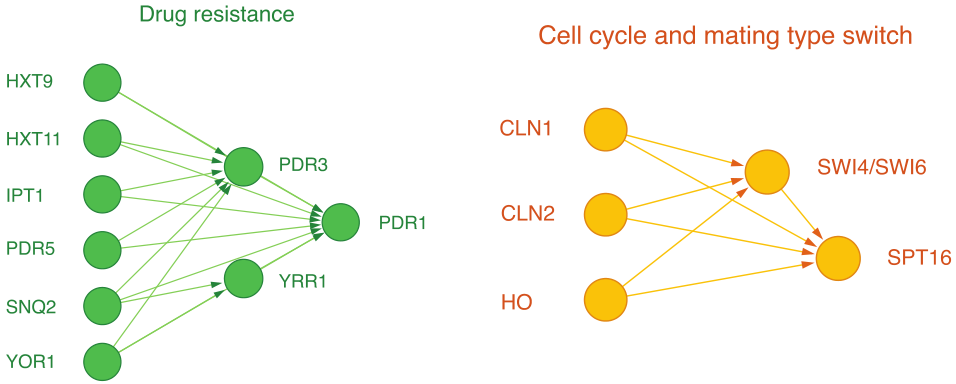
“前馈环（feed forward loops） “的motif代表生物功能。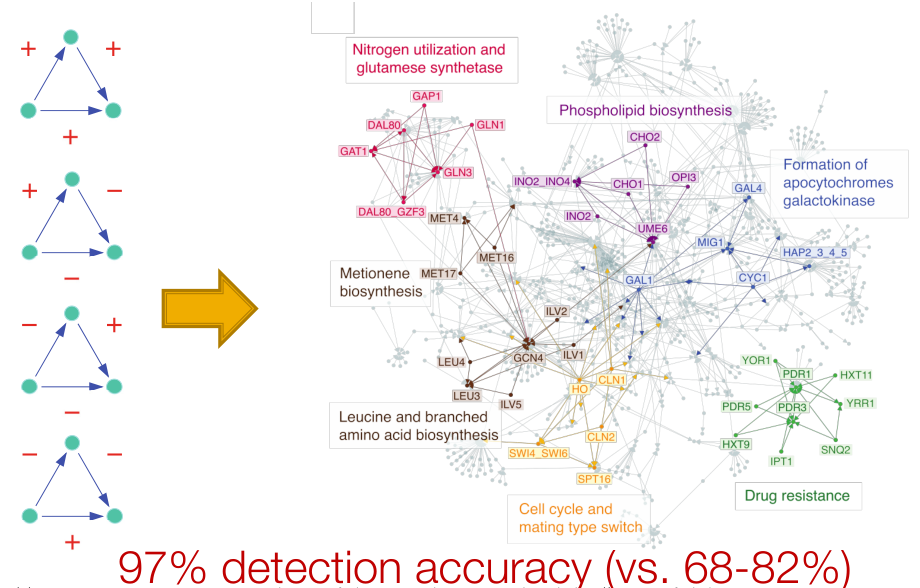
image.png
image.png

其他划分图的方法

  • METIS

启发式的，但在实践中非常有效。http://glaros.dtc.umn.edu/gkhome/views/metis

  • Graclus

基于核k均值。https://www.cs.utexas.edu/users/dml/Software/graclus.html

  • Louvain

基于模块化优化。https://perso.uclouvain.be/vincent.blondel/research/louvain.html

  • Clique percorlation method

为了寻找重叠的类别。

参考链接

知乎笔记：https://zhuanlan.zhihu.com/p/139577332
PPT：http://web.stanford.edu/class/cs224w/slides/05-spectral.pdf