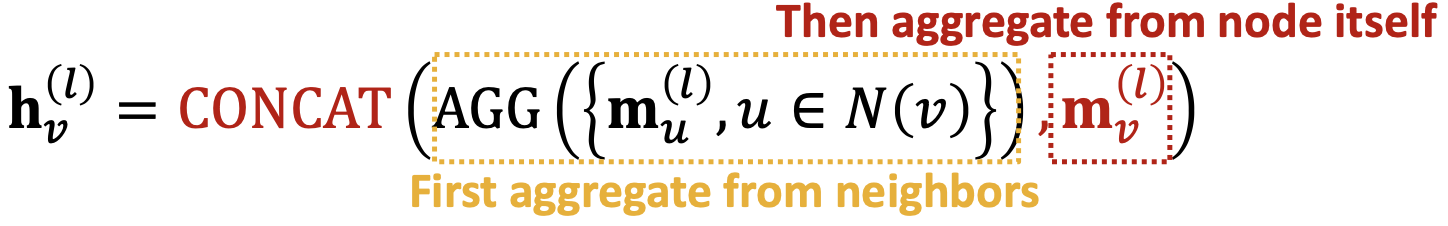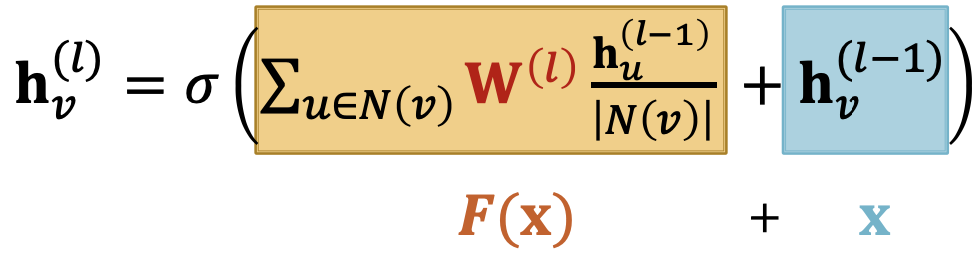回顾
回顾:Deep Graph Encoders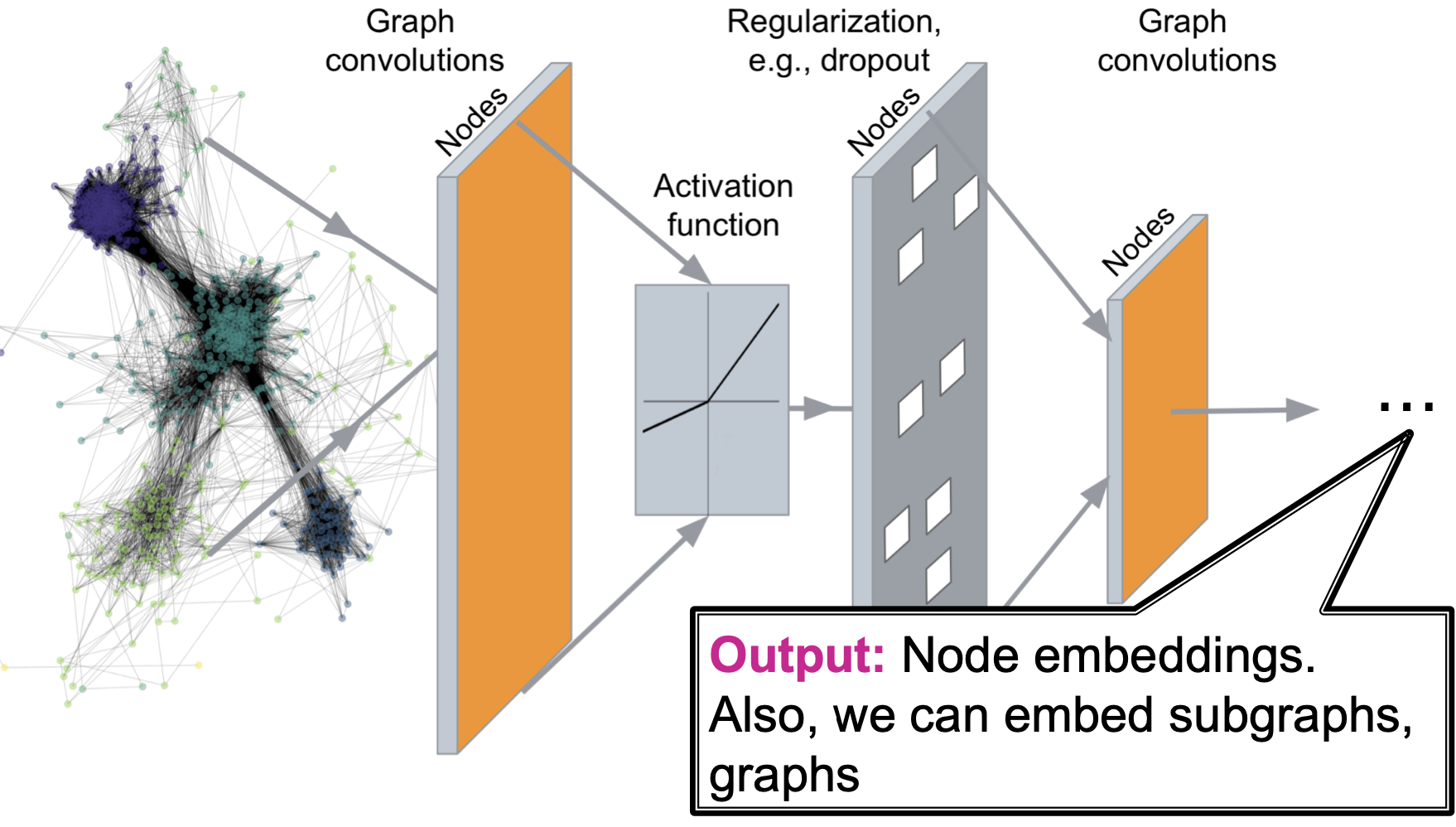
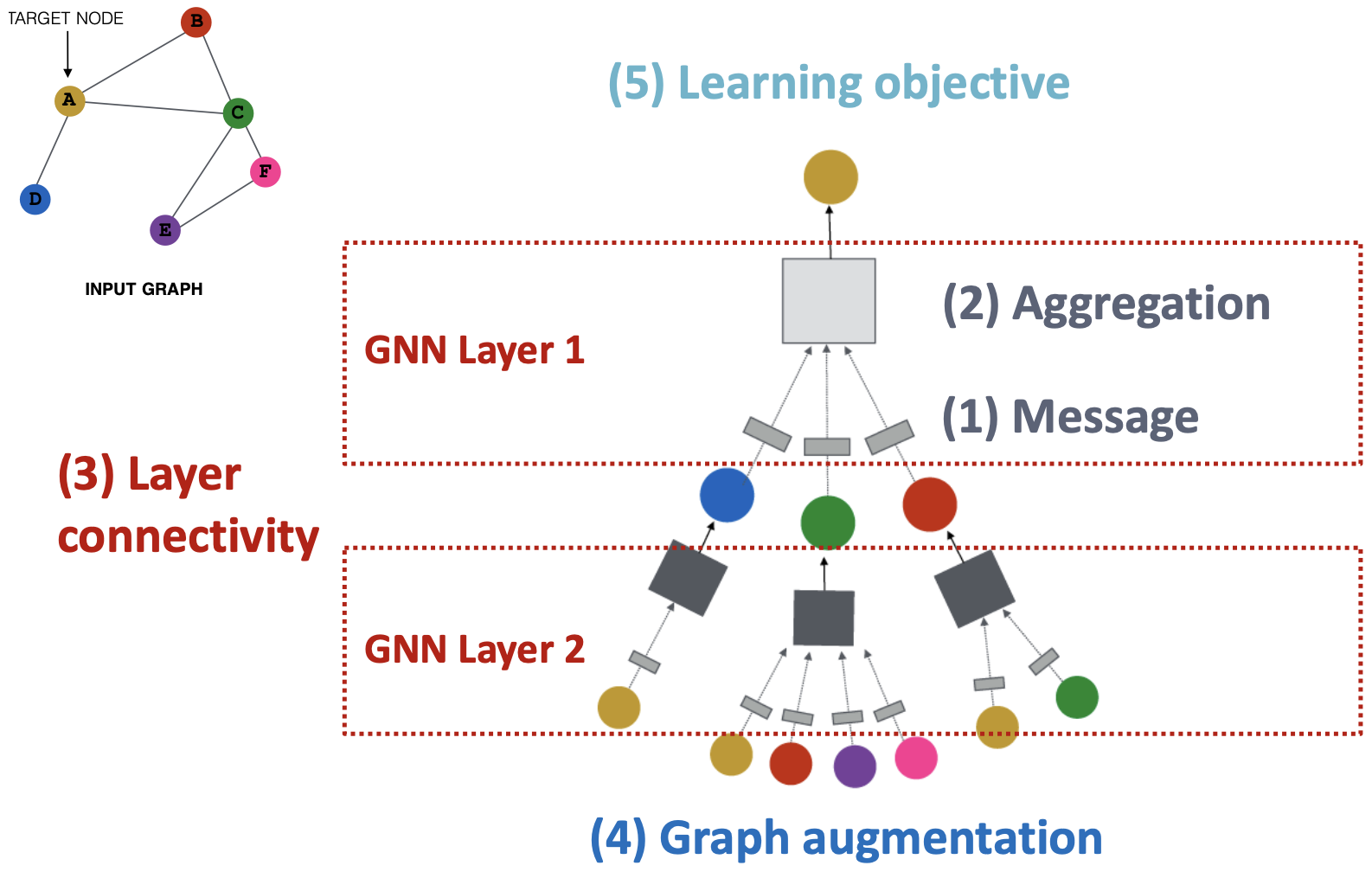
回顾:Graph Neural Networks
思想:节点的邻域定义一个计算图。学习如何通过图传播信息来计算节点特征。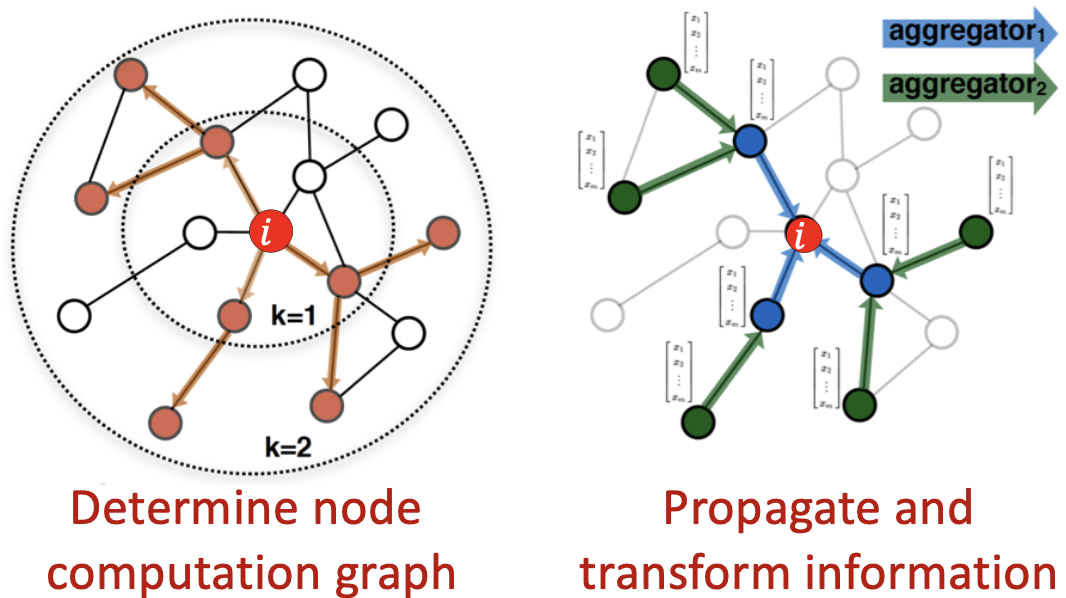
回顾:来自邻居的聚合
直觉上,节点聚合信息来自其使用神经网络的邻居。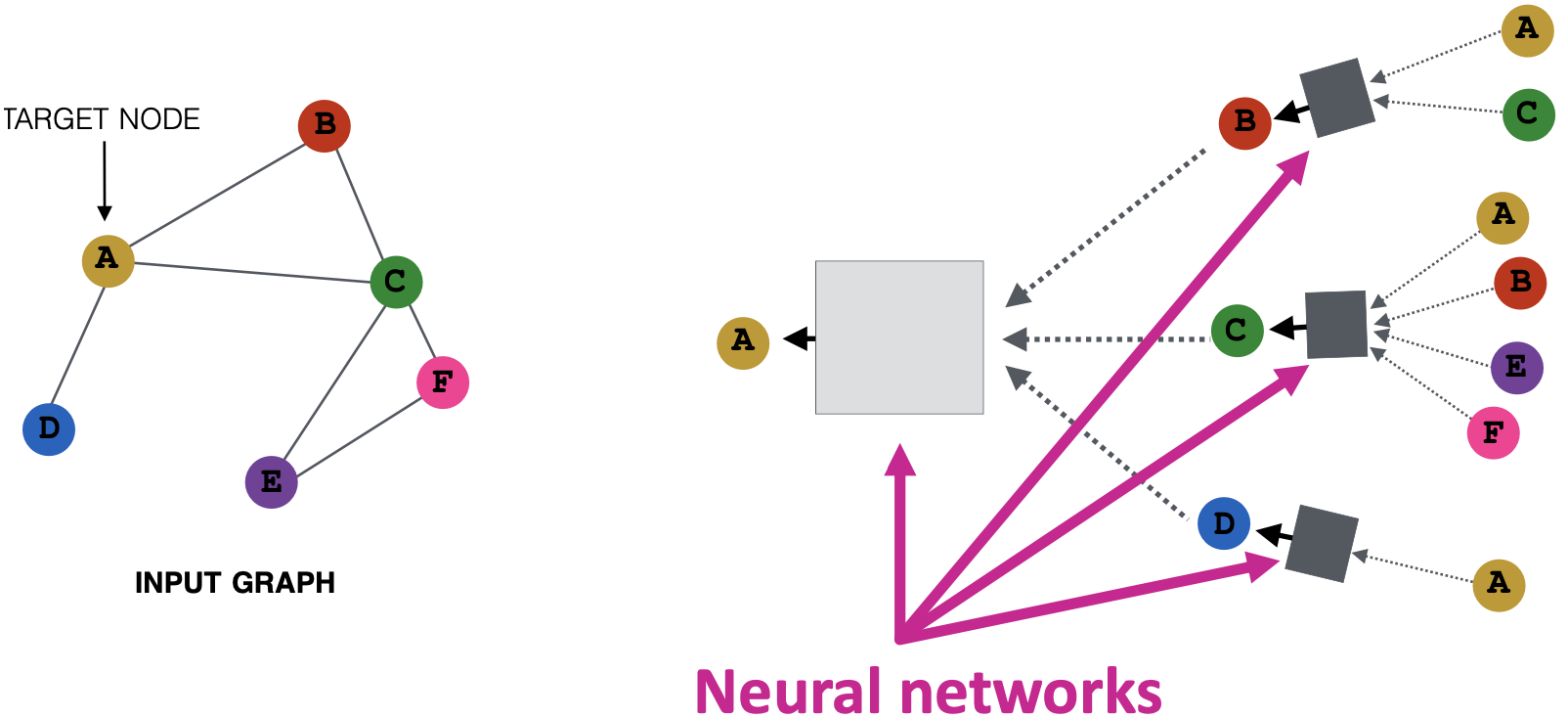
回顾:聚合邻居
直觉上,网络邻域定义了一个计算图。每个节点根据其邻域定义一个计算图!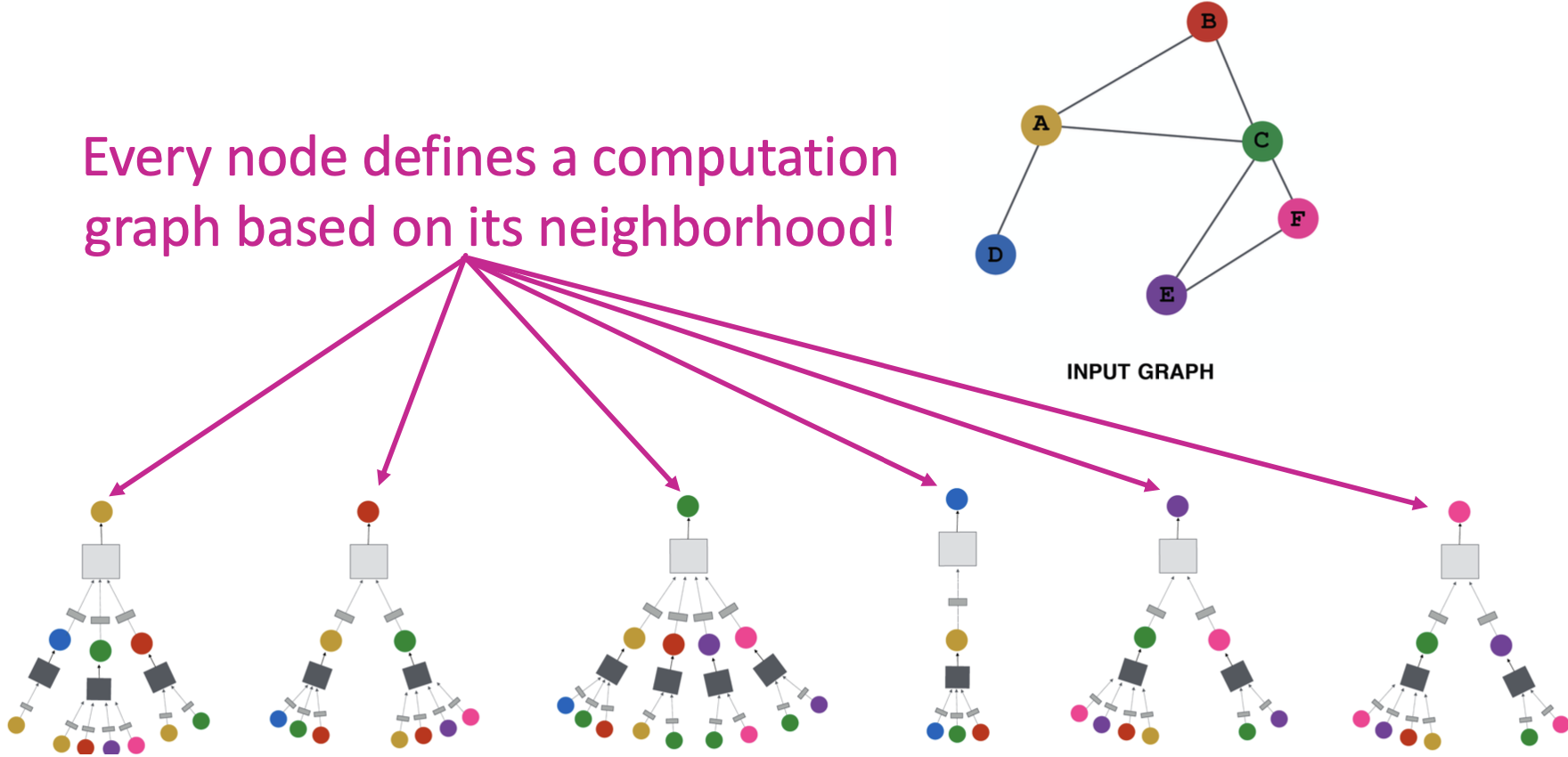
A General Perspective on Graph Neural Networks
J. You, R. Ying, J. Leskovec. Design Space of Graph Neural Networks, NeurIPS 2020
GNN Layer = Message + Aggregation
这个视角下的不同实例化,有GCN、GraphSAGE、GAT等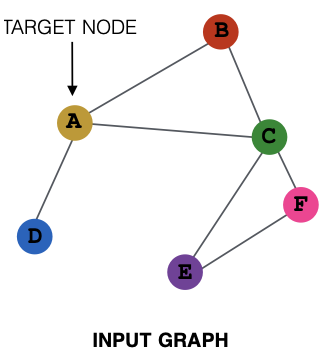
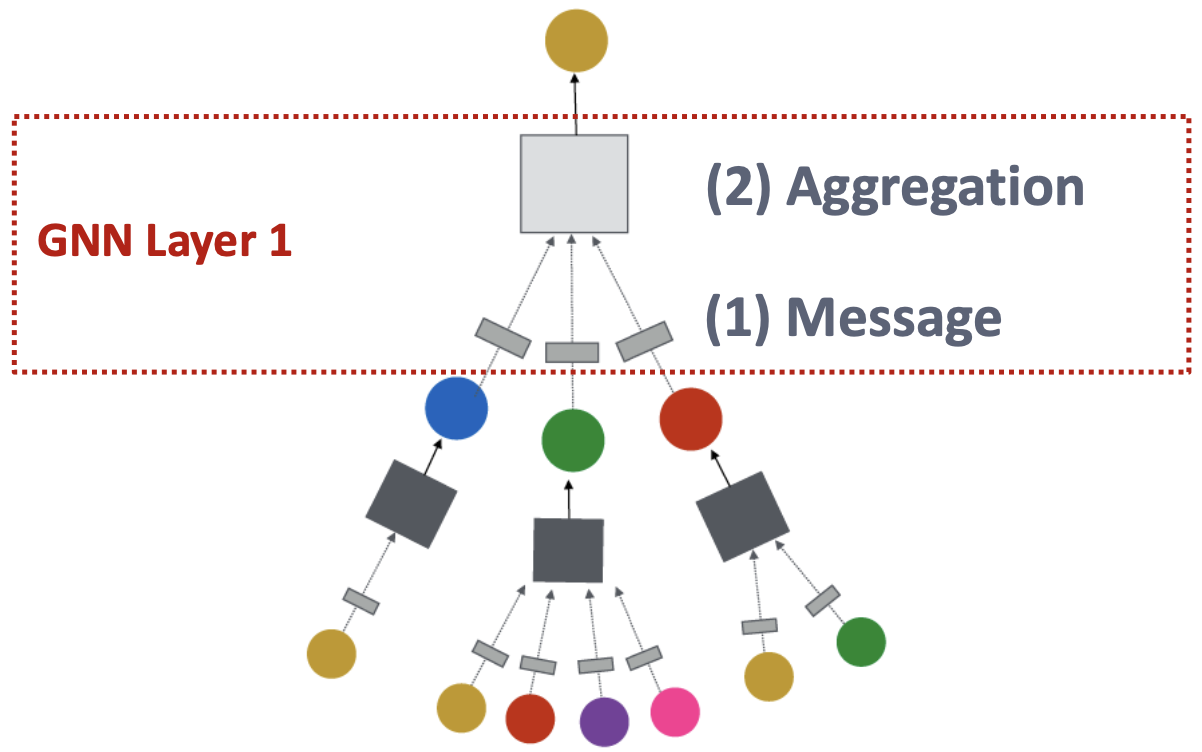
将GNN层连接到GNN中:
- 按顺序堆叠层
- 添加跳过连接的方法
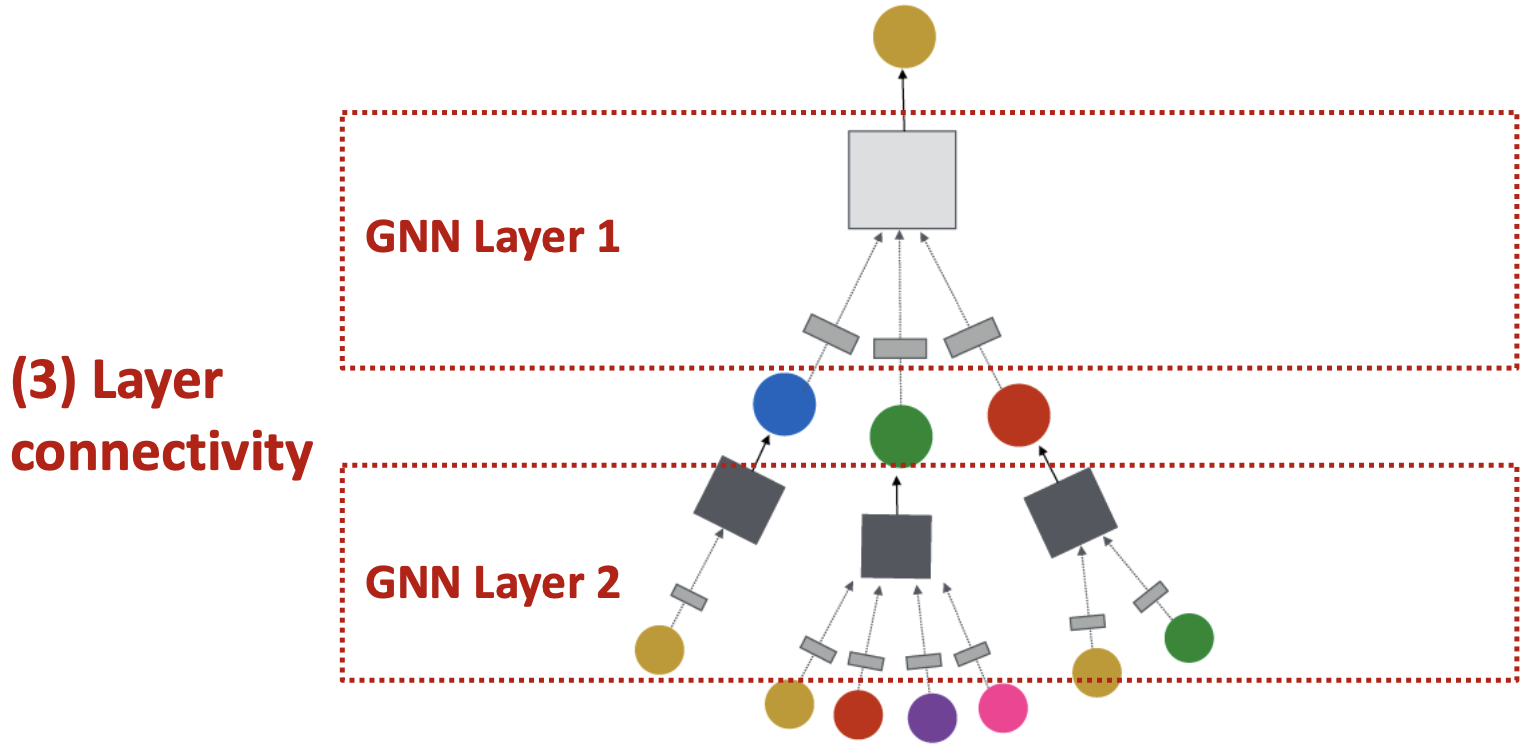
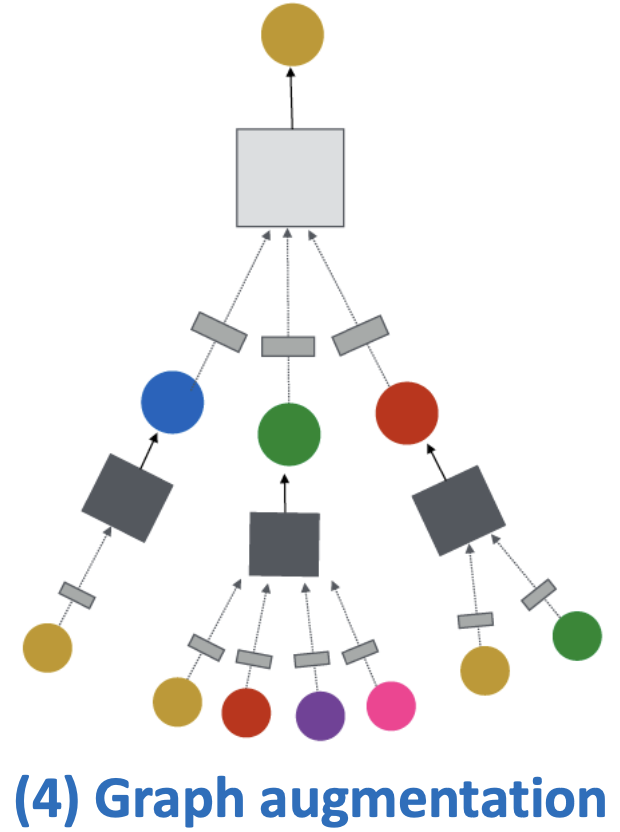
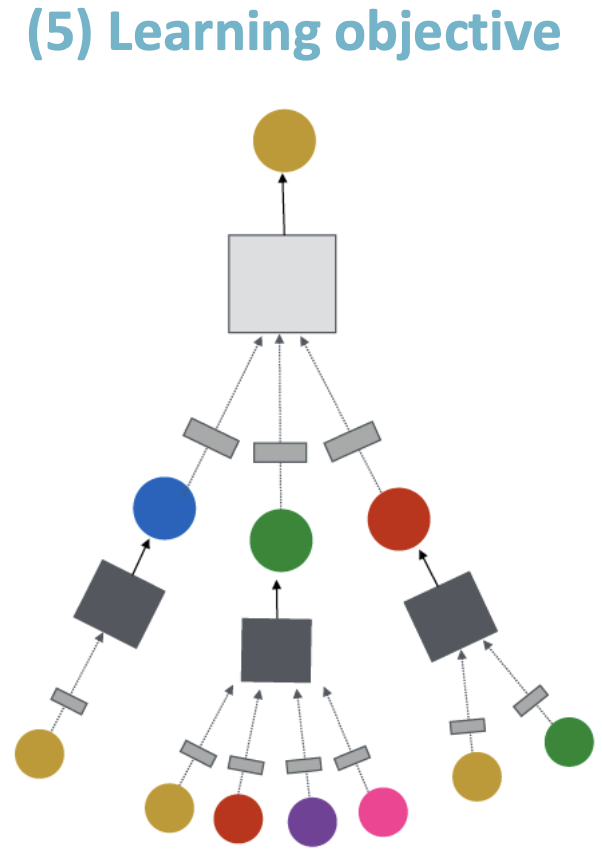
思想:“原始输入图”不等于“计算图”
- 图特征增强
- 图结构增强
我们如何训练一个GNN?
- 有监督/无监督目标
- 节点/边/图level目标
A Single Layer of a GNN
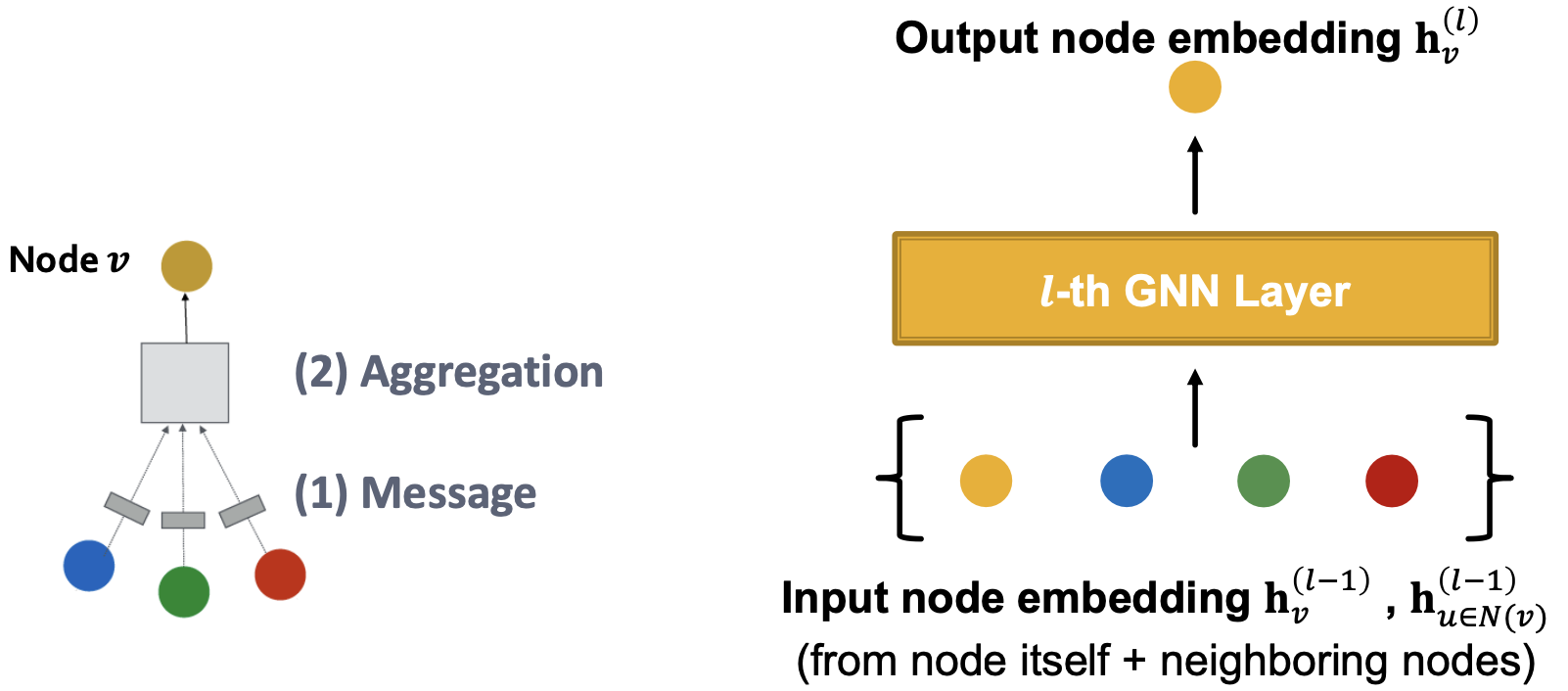
Idea of a GNN Layer:将一组向量压缩为单个向量,两个步骤:
- 消息
- 聚合
消息、聚合
消息计算
消息函数:
直觉上,每个节点将创建一条消息,该消息稍后将发送给其他节点。
如,线性层,将节点特征与权重矩阵
相乘。
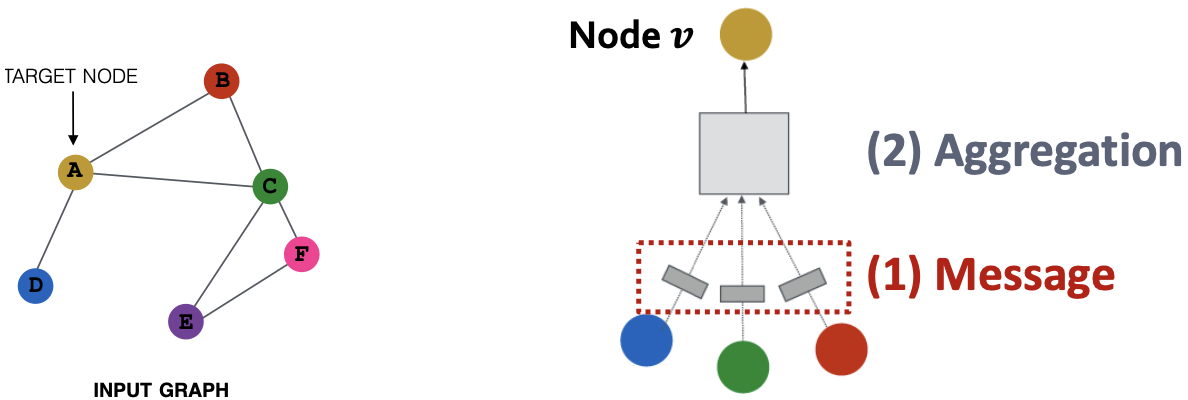
消息聚合
直觉上,每个节点将聚合来自节点的邻居的消息,
,如聚合器AGG可为Sum、Mean或Max,
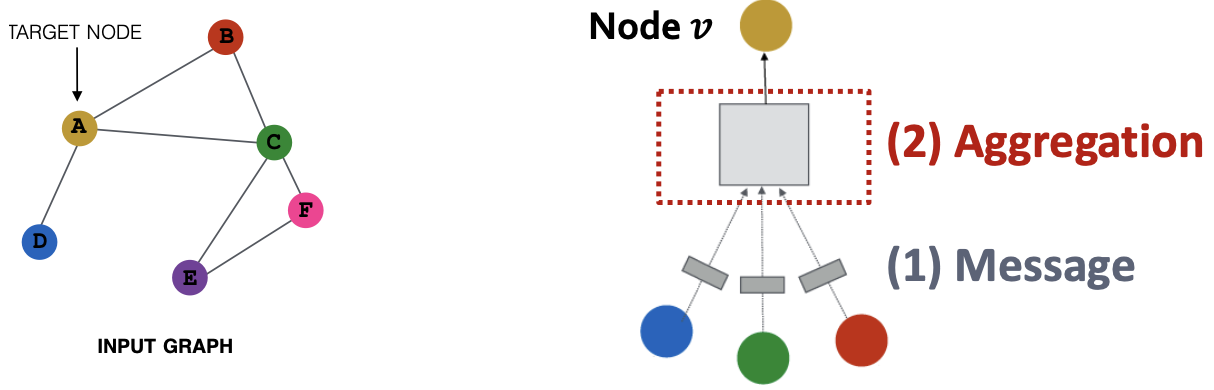
消息聚合:问题
Issue:来自节点的信息它本身可能会迷失,
的计算不是直接依赖于
。
解决方法:当计算时包括
,
- 消息:计算来自节点
自身的消息。通常,将执行不同的消息计算
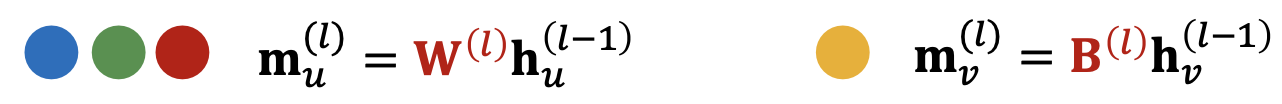
- 聚合:在从邻居聚合之后,可以聚合来自节点
的自身消息,通过串联或求和
summary
- 消息:每个节点计算一个消息,
- 聚合:聚合来自邻居的消息,
非线性(激活):增加表达。常记为
,如
等。可以添加到消息或聚合中。
Classical GNN Layers
Classical GNN Layers: GCN
GCN:
,写作“消息+聚合”形式有
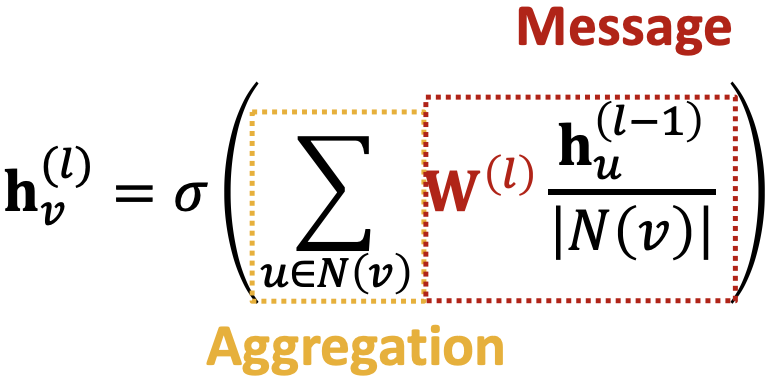
按节点度归一化(在GCN论文中,他们使用了稍微不同的标准化)消息:每个邻居
-
Classical GNN Layers: GraphSAGE
Hamilton et al. Inductive Representation Learning on Large Graphs, NeurIPS 2017
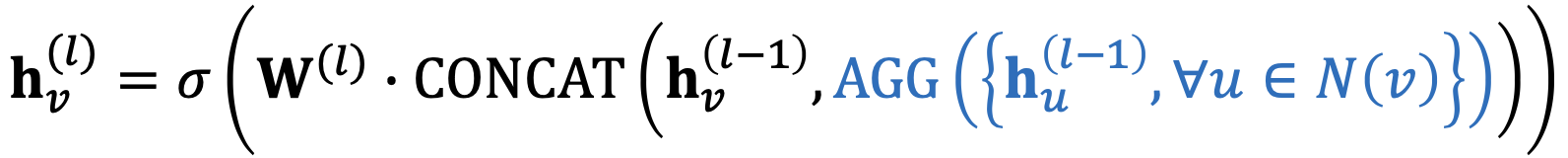
如何写成“消息+聚合”?
消息在中计算
聚合两个步骤: stage1:从节点邻居聚合,
- stage2:在节点本身上进一步聚合,
GraphSAGE邻居聚合:
- Mean:取邻居的加权平均数,
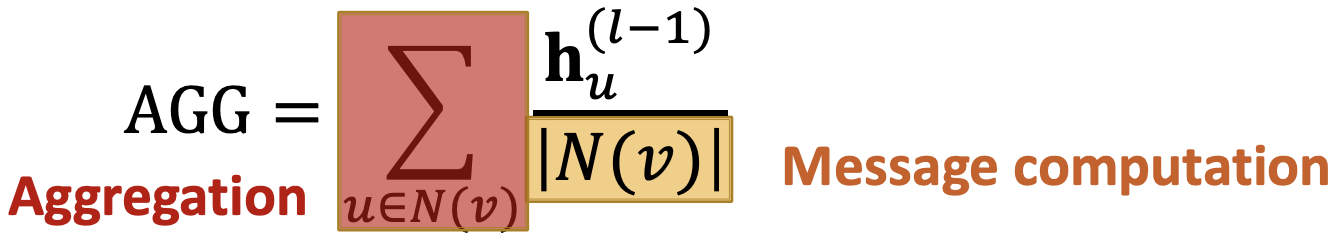
- Pool:变换邻域向量并应用对称向量函数Mean or Max,
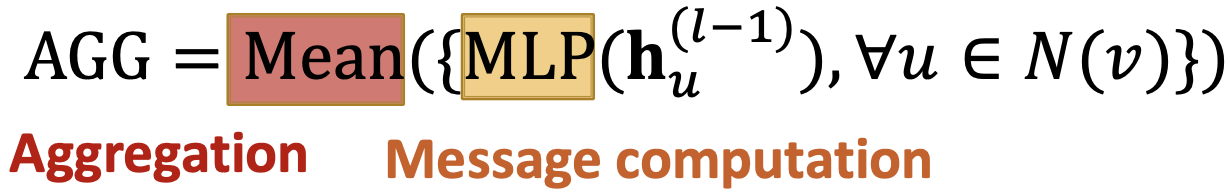
- LSTM:将LSTM用于重组的邻居,
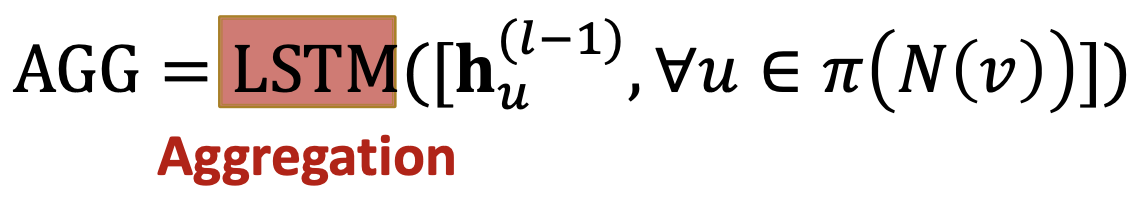
GraphSAGE的L2范化:
可选的,在每层对使用L2范化。
(
范数)
- 没有
范数,嵌入向量有不同尺度(
范数)
- 在某些情况下(并非总是),嵌入的范化会提高性能
-
Classical GNN Layers: GAT
Graph Attention Networks
,其中
是Attention weights。
在GCN/GraphSAGE中,有: 是节点
的消息对节点
的权重因子(重要性);
是基于图的结构属性(节点度)明确定义的;
所有邻居
对节点
同等重要。
但并不是所有节点的邻居都是同等重要的,Attention受到认知注意力的启发,attention关注的是输入数据的重要部分,而不是其他部分。
- 想法:神经网络应该在数据的小而重要的部分投入更多的计算能力。
- 哪部分数据更重要取决于上下文,并通过训练学习。
我们能做得比简单的邻居聚合更好吗?我们可以让权重因子被学习吗?
goal:指定图中每个节点的不同邻居的任意重要性。
idea:计算图中每个节点按照注意策略的嵌入。节点会接收邻居的信息,隐式地指定邻域中不同节点的不同权重。
设通过计算后为一个注意机制
,让
通过节点对
的信息计算注意力系数
:
,
表示节点
对消息对节点
对重要性。
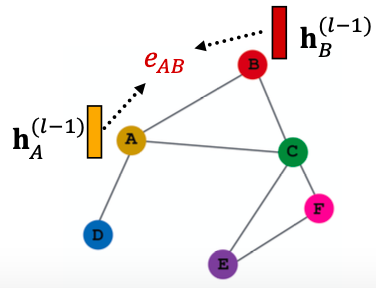
将归一化为最终注意力权重
,即
基于最终注意力权重的加权和,
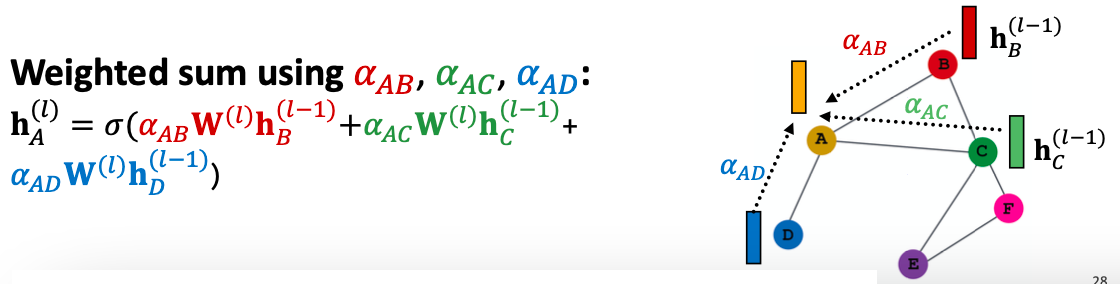
注意力机制的形式是什么?该方法与
的选择无关,如使用简单的单层神经网络,
具有可训练的参数(线性层中的权重)。
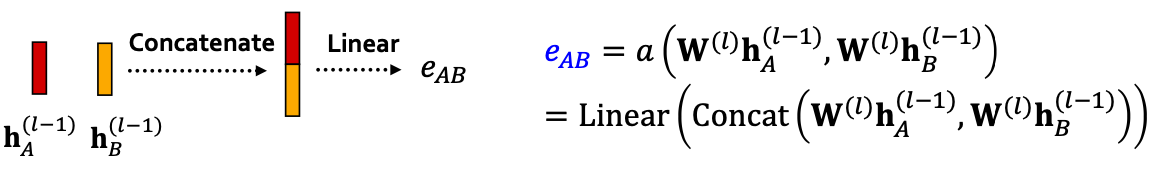
的参数是联合训练的,以端到端方式学习参数和权重矩阵(即神经网络的其他参数
)。
多头注意力:稳定注意力机制的学习过程。
创建多个注意力分数(每个副本具有一组不同的参数):
输出是聚合,通过串联或求和,
注意力机制的好处:
- 关键好处:允许隐式指定对不同邻居的不同重要性
- 计算效率:
- 注意力系数的计算可以在图的所有边上并行化
- 聚合可以在所有节点上并行化
- 存储效率:
- 稀疏矩阵操作不需要存储
以上条目
- 固定数量的参数,无论图的大小
- 稀疏矩阵操作不需要存储
- 局部化:只在局部网络邻域参加
- 归纳能力:
- 这是一个共享的edge-wise机制
- 它不依赖于全局图结构
GAT例子:Cora Citation Net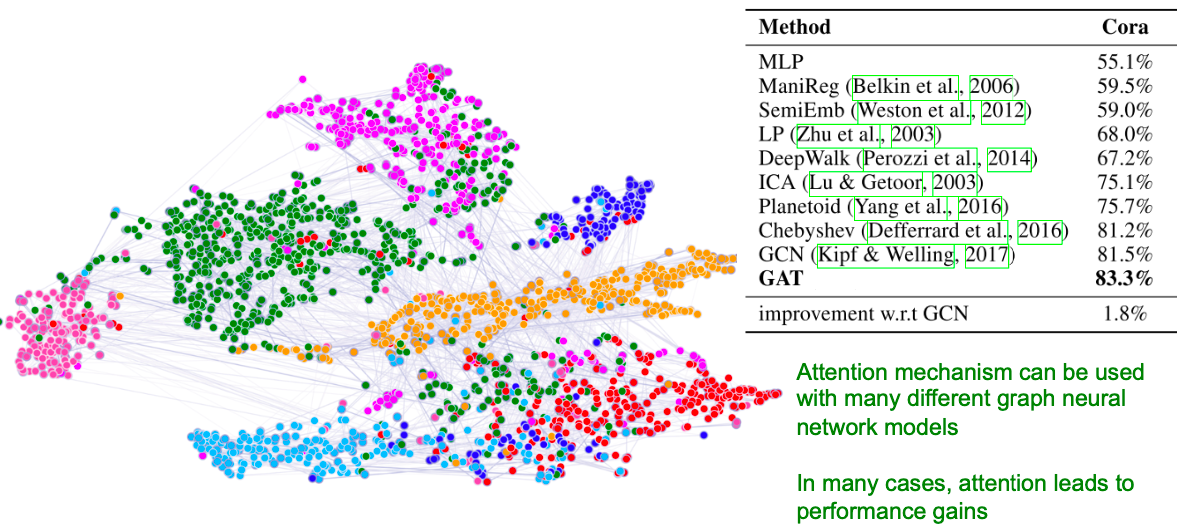
注意力机制可用于多种不同的图神经网络模型,在许多情况下,注意力会带来性能收益。
基于GAT的节点嵌入的t-SNE图:
- 节点颜色:7中出版类型
-
GNN Layer in Practice
J. You, R. Ying, J. Leskovec. Design Space of Graph Neural Networks, NeurIPS 2020
实际上,这些经典的GNN层是一个很好的起点。我们通常可以通过考虑通用GNN层设计来获得更好的性能。具体来说,我们可以包括在许多领域被证明有用的现代深度学习模块。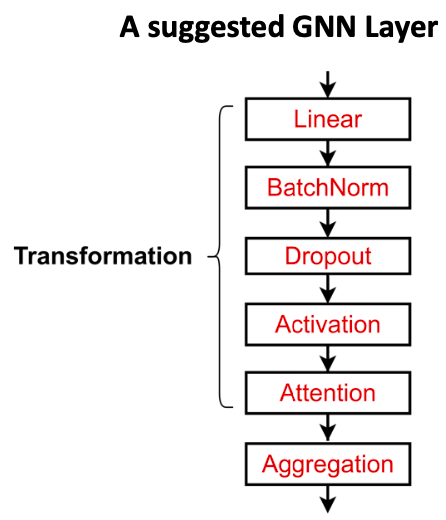
许多现代深度学习模块都可以整合到GNN层中: Batch Normalization:稳定神经网络训练
- Dropout:防止过拟合
- Attention/Gating:控制消息的重要性
-
Batch Normalization
S. Loffe, C.Szegedy. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, ICML 2015
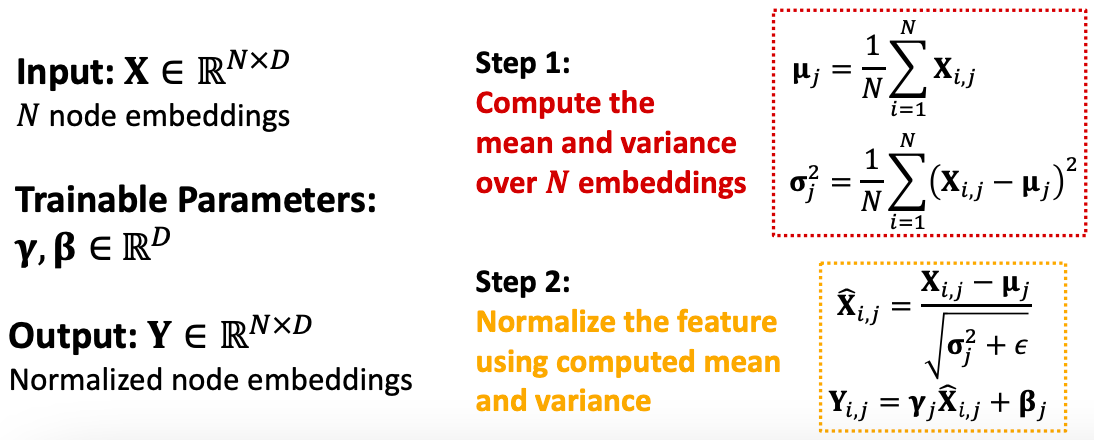
目标:稳定神经网络训练
思想:给定一批输入(节点嵌入), 将节点嵌入重新居中为零均值;
- 将方差重新缩放为单位方差。
Dropout
Srivastava et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting, JMLR 2014
目标:正则化神经网络以防止过拟合。
思想:
- 在训练过程中,以一定的概率
,随机设置神经元为0(关闭)
- 在测试期间,使用所有神经元进行计算
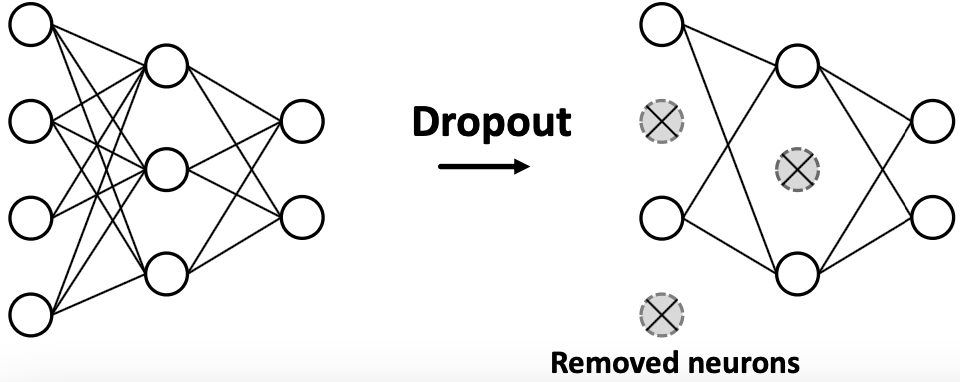
在GNN中,Dropout应用于消息函数中的线性层。一个简单的线性层消息函数可为: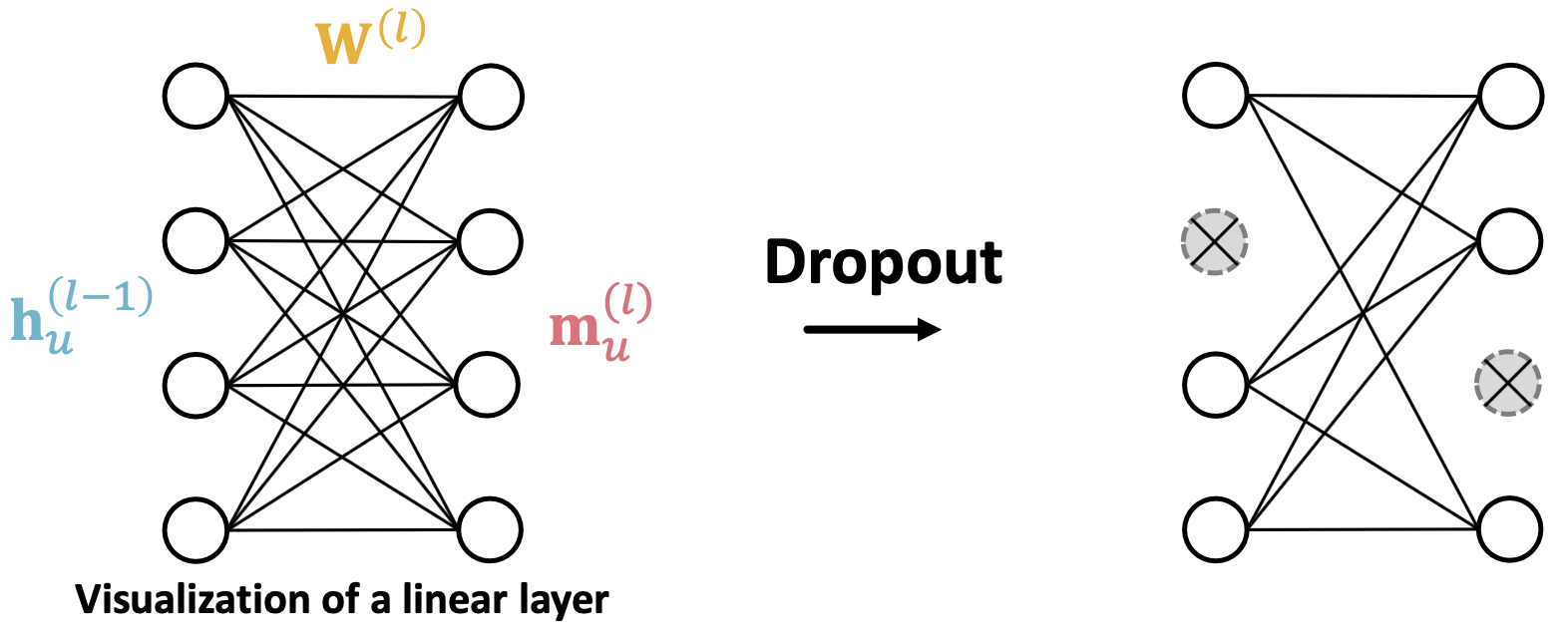
Activation (Non-linearity)
将激活应用于嵌入的第
维
- Rectified linear unit (ReLU):
最常用的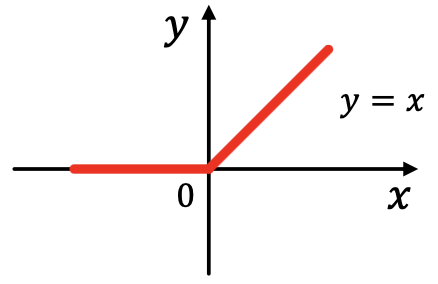
- Sigmoid:
仅在要限制嵌入范围时使用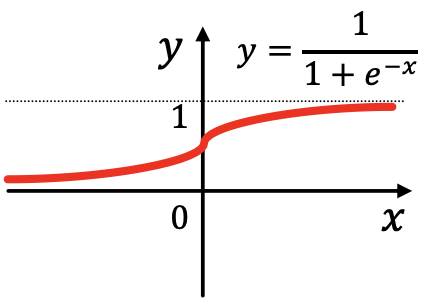
- Parametric ReLU
Summary
现代深度学习模块可以包含在GNN层中,以获得更好的性能。
设计新颖的GNN层仍然是一个活跃的研究前沿!
建议资源:可以探索不同的GNN设计,或者在GraphGym中尝试你自己的想法。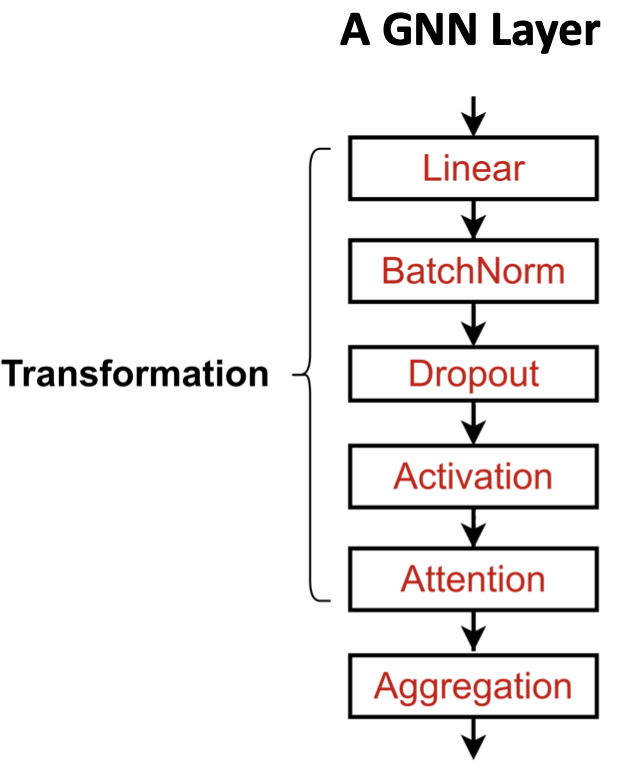
Stacking Layers of a GNN
Stacking GNN layers:
J. You, R. Ying, J. Leskovec. Design Space of Graph Neural Networks, NeurIPS 2020
如何将GNN层连接到GNN中?
- 按顺序堆叠层
- 添加跳过连接的方法
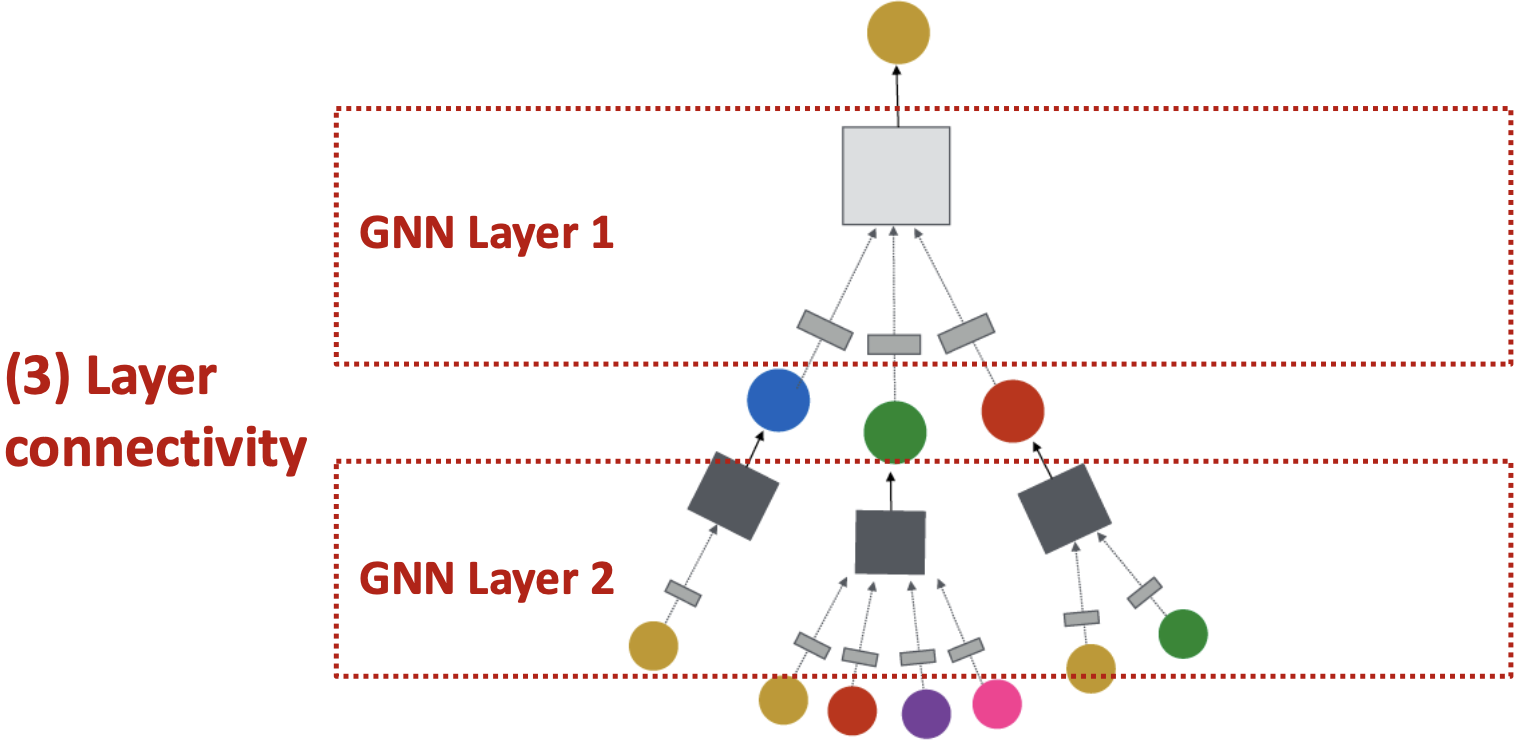
如何构建图神经网络?
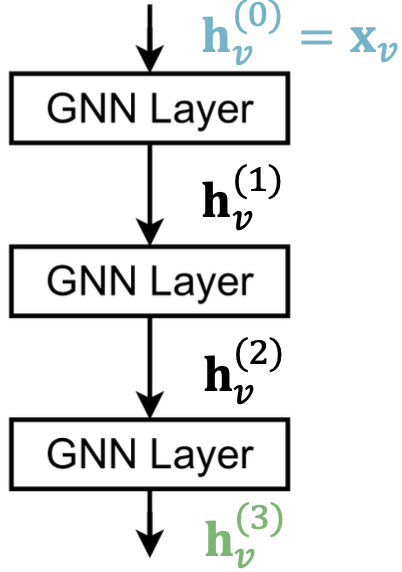
- 标准方法:按顺序堆叠GNN层
- 输入:初始原节点特征
- 输出:
层GNN后的节点嵌入
过度平滑与感受野
过度平滑问题:
堆叠多个GNN层的问题是GNN会存在过度平滑问题。
过度平滑问题(over-smoothing):所有节点嵌入都收敛到相同的值。
这很糟糕,因为我们想使用节点嵌入来区分节点。
为什么会出现过度平滑的问题?
感受野(receptive field):决定感兴趣节点嵌入的一组节点。
在第层GNN中,每个节点都有一个K-hop邻域的感受野。
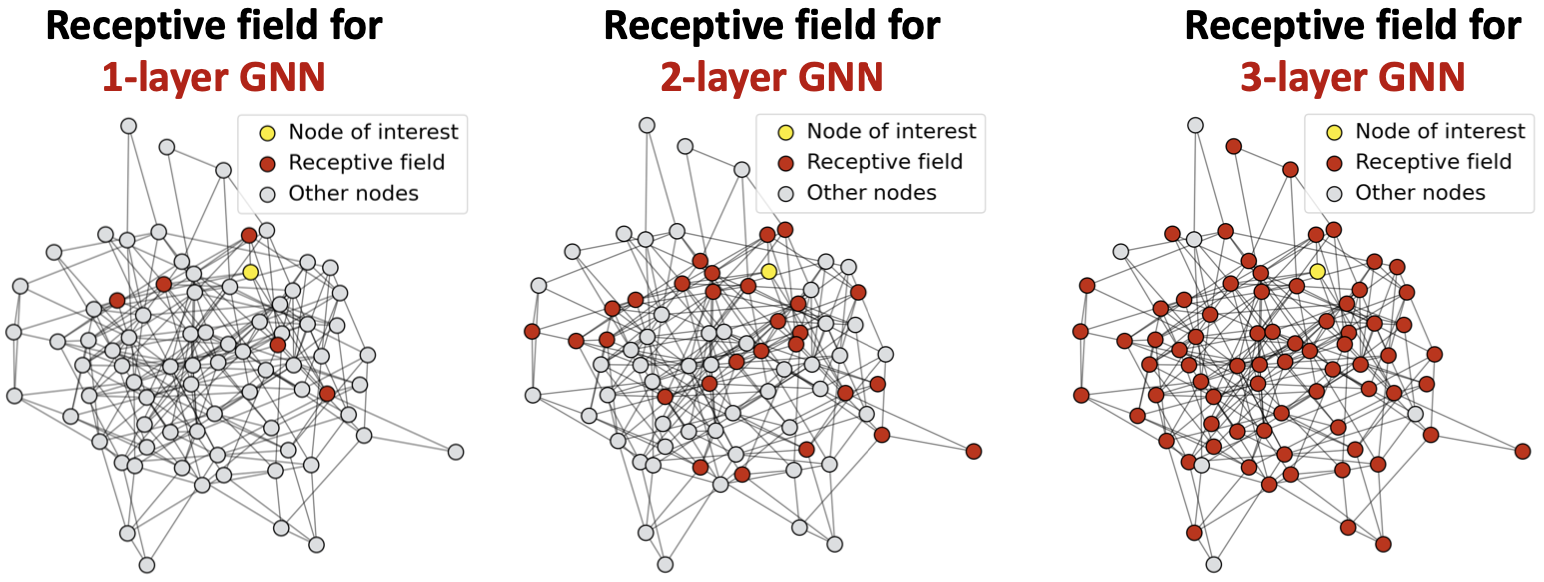
两个节点的感受野重叠,当我们增加跳数(GNN层数)时,共享邻居迅速增长。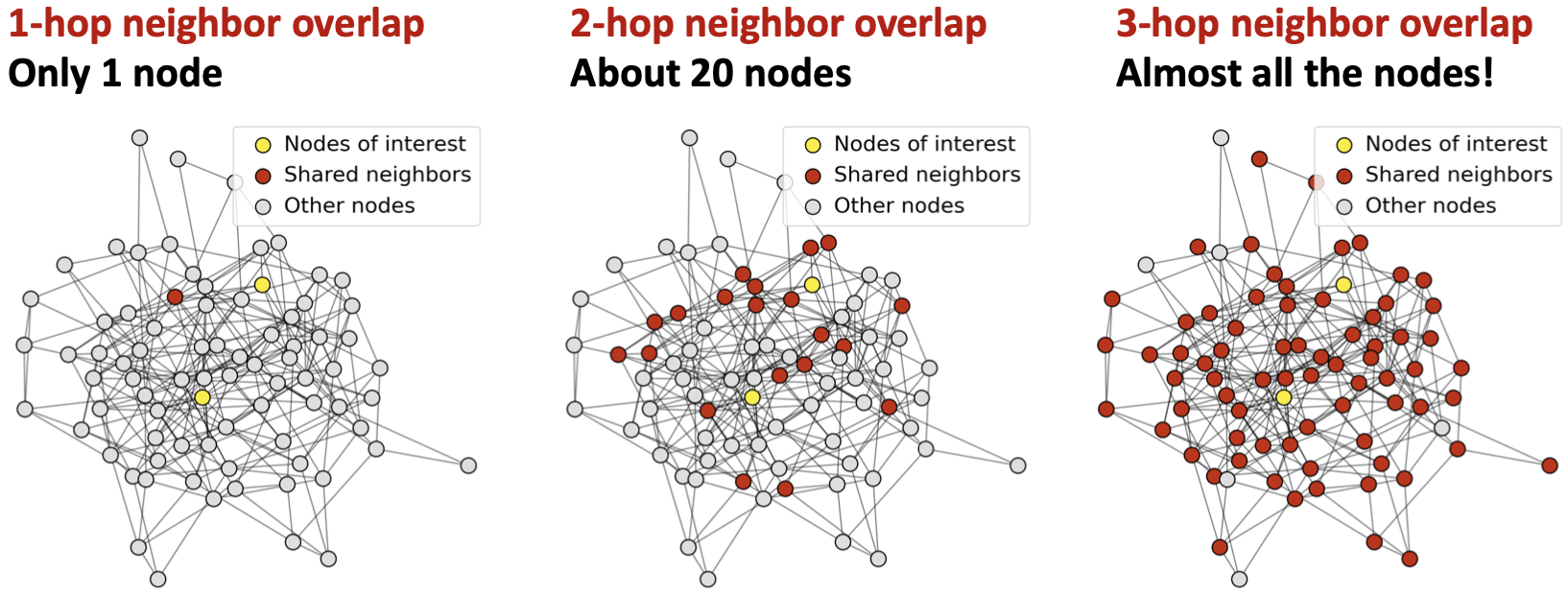
感受野的概念可以用来解释过度平滑。
由于节点的嵌入是由其感受野决定的,那么如果两个节点的感受野高度重叠,则它们的嵌入高度相似。
堆叠多个GNN层 -> 节点的感受野高度重叠 -> 节点嵌入高度相似 -> 存在过度平滑问题
我们如何克服过度平滑问题?
设计GNN层连接
第一点 添加GNN层时要小心
- 与其他领域的神经网络(CNN用于图像分类)不同,添加更多的GNN层并不总是有帮助。
- Step1:分析解决问题所需的感受野。例如,通过计算图形的直径。
- Step2:设置GNN层的数量
比感受野多一点,但不要设定
太大。
问题:如果GNN层的数量较少,如何增强GNN的表达能力?
如何让浅薄的GNN更具表现力?
解决方案1:增加每个GNN层的表达能力。
在前面的示例中,每个变换或聚合函数只包含一个线性层,我们可以让聚合/转换变成一个深度神经网络。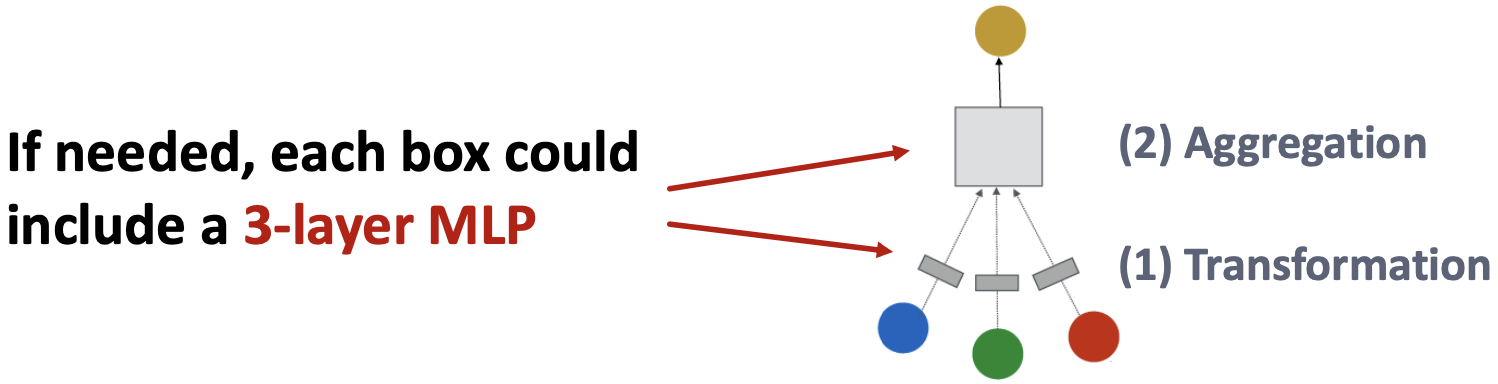
解决方案2:添加不传递消息的层。
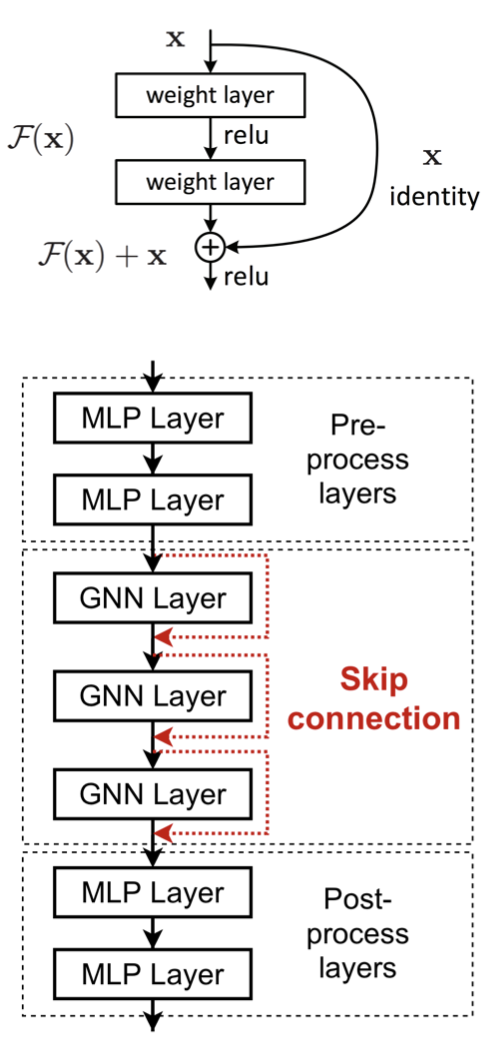
GNN不一定只包含GNN层。例如,我们可以在GNN层之前和之后添加MLP层(应用于每个节点),作为预处理层和后处理层。
预处理层:当需要编码节点特征时很重要。例如,当节点代表图像/文本时。
后处理层:当需要对节点嵌入进行推理/转换时,这一点很重要。例如,图分类、知识图。
实际中,添加这些层非常有效!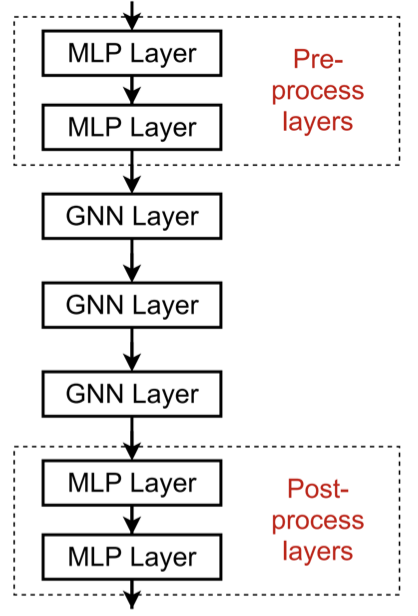
第二点 在GNNs中添加跳过连接
He et al. Deep Residual Learning for Image Recognition, CVPR 2015
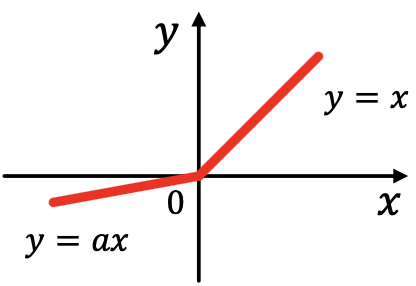
来自过度平滑的观察:早期GNN层中的节点嵌入有时可以更好地区分节点。
解决方案:通过在GNN中添加捷径(shortcuts),我们可以增加早期层对最终节点嵌入的影响。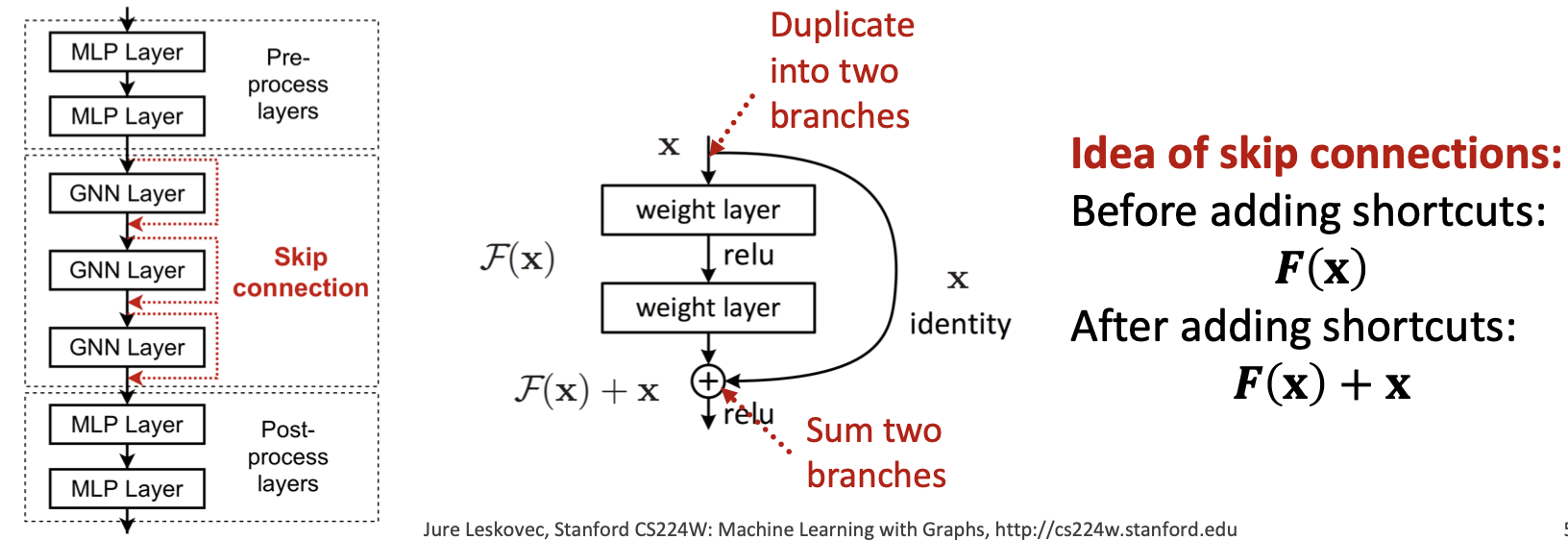
为什么跳过连接有效?
Veit et al. Residual Networks Behave Like Ensembles of Relatively Shallow Networks, ArXiv 2016
直觉上,跳过连接创建了一个混合模型。
N skip连接 -> 条可能的路径
每条路径可能有多达模块
我们自动得到浅GNN和深GNN的一个混合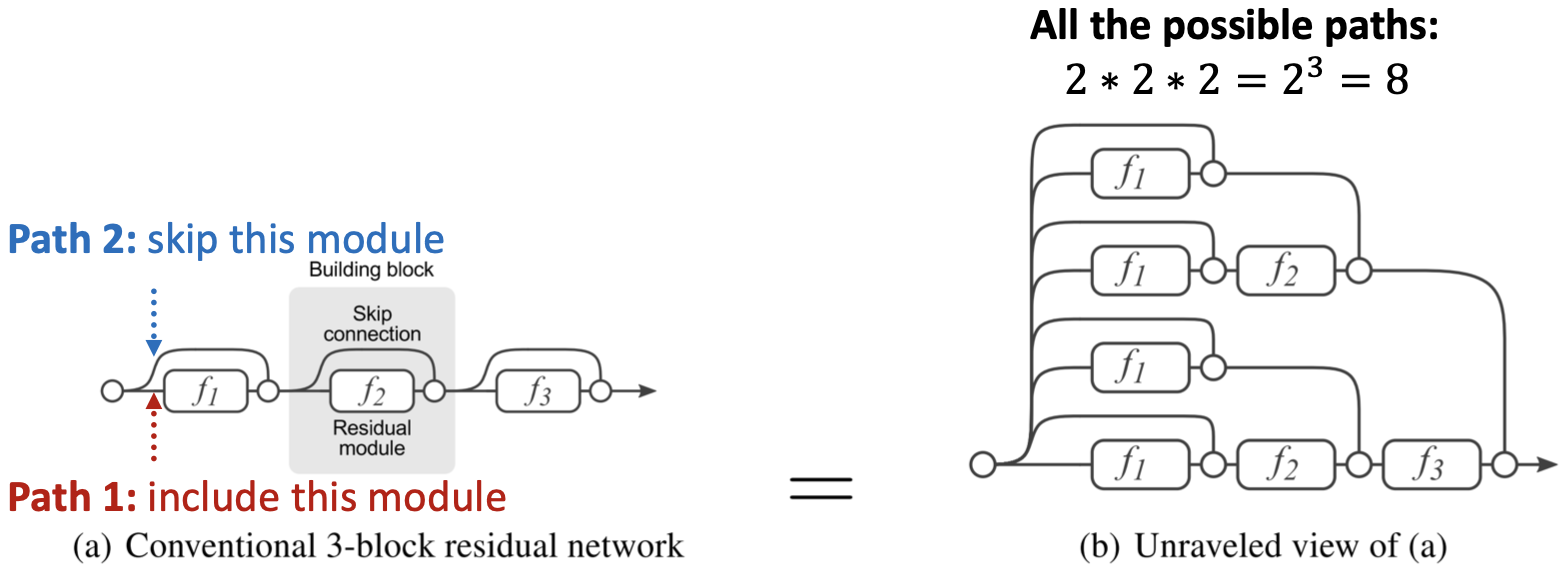
例子:带跳过连接的GCN
跳过连接的其他选择
Xu et al. Representation learning on graphs with jumping knowledge networks, ICML 2018
直接跳到最后一层,最后一层直接从前一层的所有节点嵌入中聚合。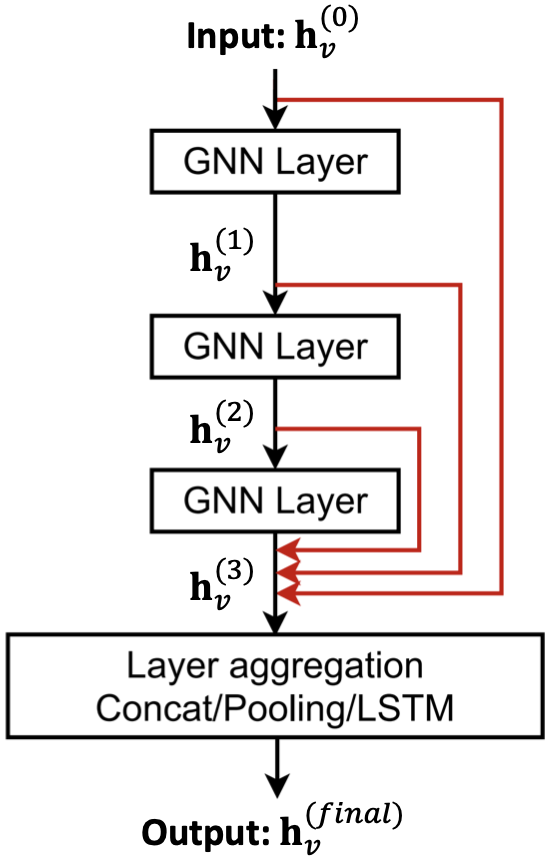
Graph Manipulation in GNNs
通用GNN框架:
J. You, R. Ying, J. Leskovec. Design Space of Graph Neural Networks, NeurIPS 2020
Idea:“原始输入图” 不等于 “计算图”
- 图特征增强
- 图结构处理
为什么处理图?
到目前为止,我们的假设是“原始输入图” 等于 “计算图”,打破这一假设的原因如下:
- 特征层面:输入图缺少特征 -> 图增强
- 结构层面:
- 图太稀疏 -> 低效的消息传递
- 图太密集 -> 消息传递成本太高
- 图太大 -> 无法将计算图放入GPU
-
图处理的方法
图特征处理:
- 输入图缺少特征:图增强
图结构处理
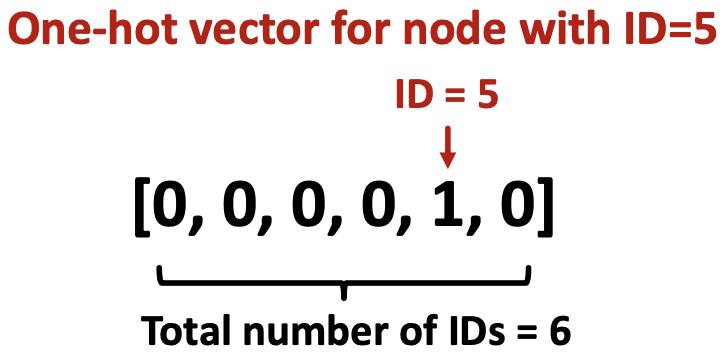
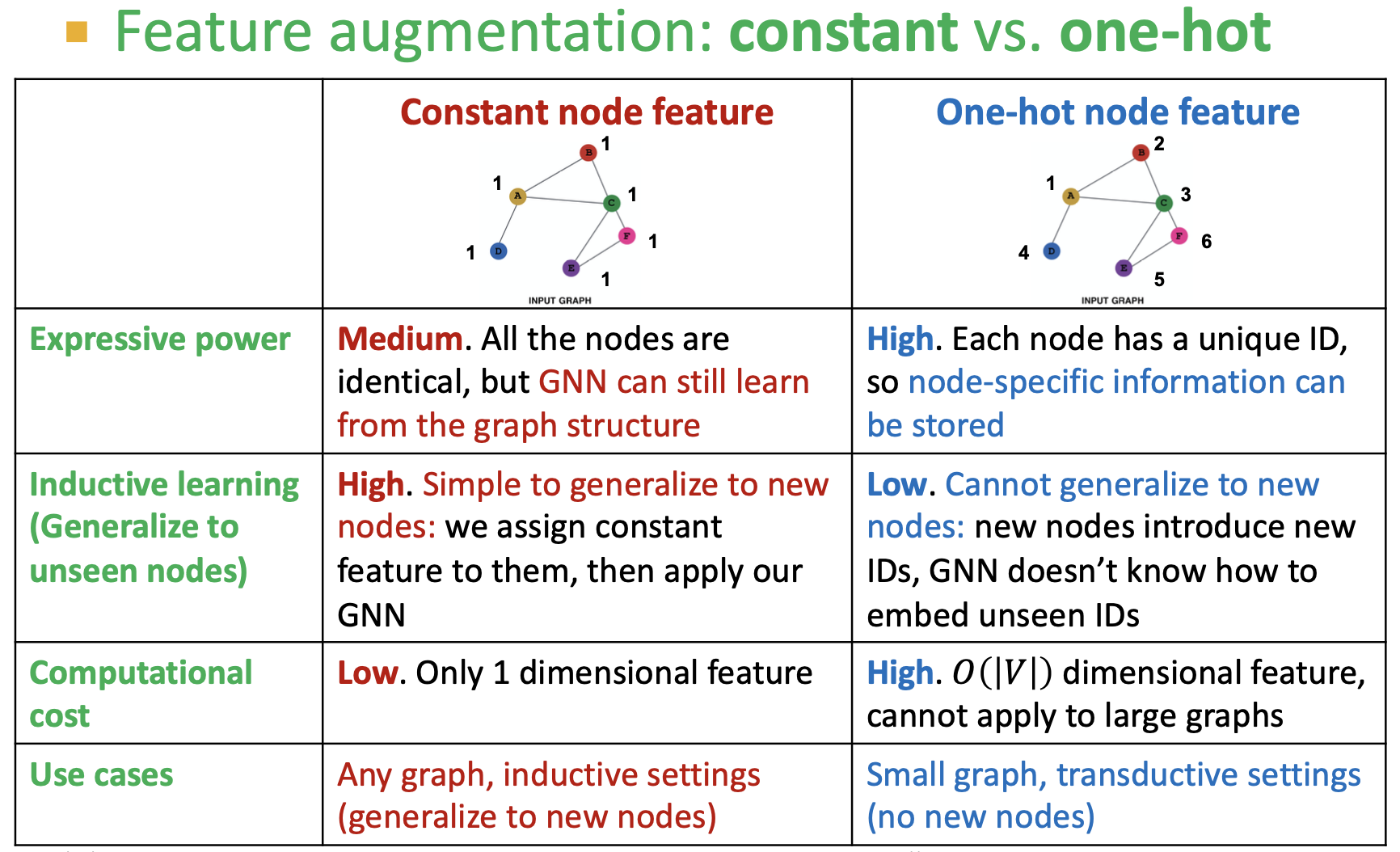
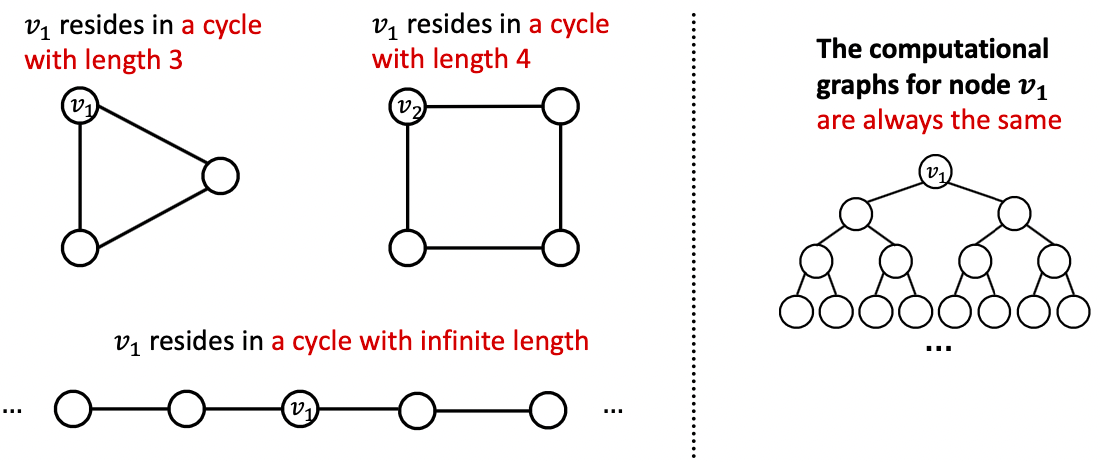
为什么需要特征增强?理由2: 某些结构很难通过GNN学习,如循环计数特征。
- GNN不能学习到
所在的周期的长度。
无法区分它位于哪个图中。因为图中的所有节点度都为2,计算图会是相同的二叉树。
解决方案:可以使用循环计数作为增强节点特征。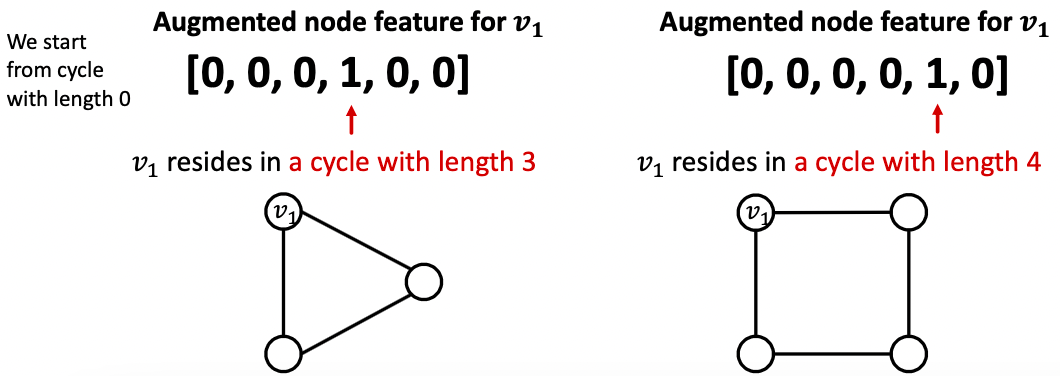
其他增强特征方法:
如二分图:
- Author-to-papers (they authored)
-
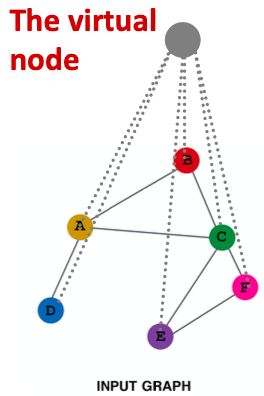
添加虚拟节点
虚拟节点将连接到图中的所有节点。
假设在一个稀疏图中,两个节点的最短路径是10
- 在添加虚拟节点后,所有节点的距离为2,如节点A - 虚拟节点 - 节点B。
节点邻域抽样
先前所有节点都被用来消息传递,可考虑(随机)采样一个节点的邻居,以便进行消息传递。
如,我们可以随机选择两个邻居来传递消息,仅使用节点B和D传递消息给节点A。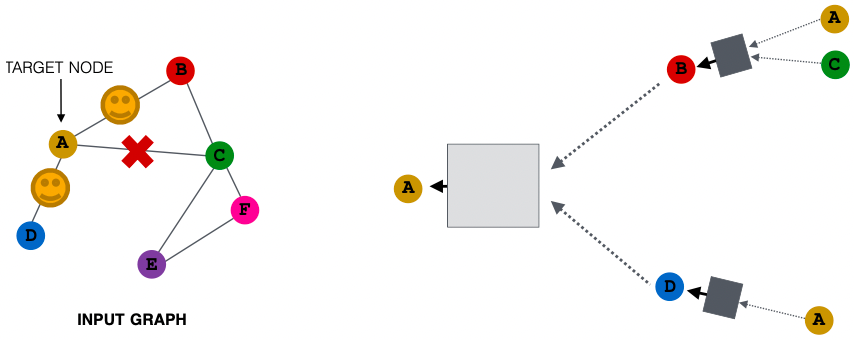
接下来计算嵌入,我们可以抽样不同邻居,仅抽样节点C和D传递消息给节点A。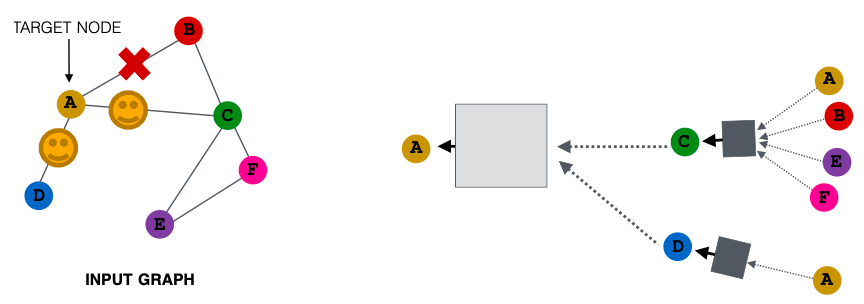
Ying et al. Graph Convolutional Neural Networks for Web-Scale Recommender Systems, KDD 2018
正如预期那样,我们可以得到类似于使用所有邻居的情况下的嵌入。
好处:大大降低计算成本,且在实践中很有效。
Summary
GNNs的一般角度:
- GNN层:
- 转换 + 聚合
- 经典GNN层:GCN、GraphSAGE、GAT
- 层连接
- 决定层的数量
- 跳过连接
- 图处理
- 特征增强
- 结构处理
下节介绍:GNN目标函数、实践中的GNN