hierarchical 阶层式;分层的;分等级的
Community定义
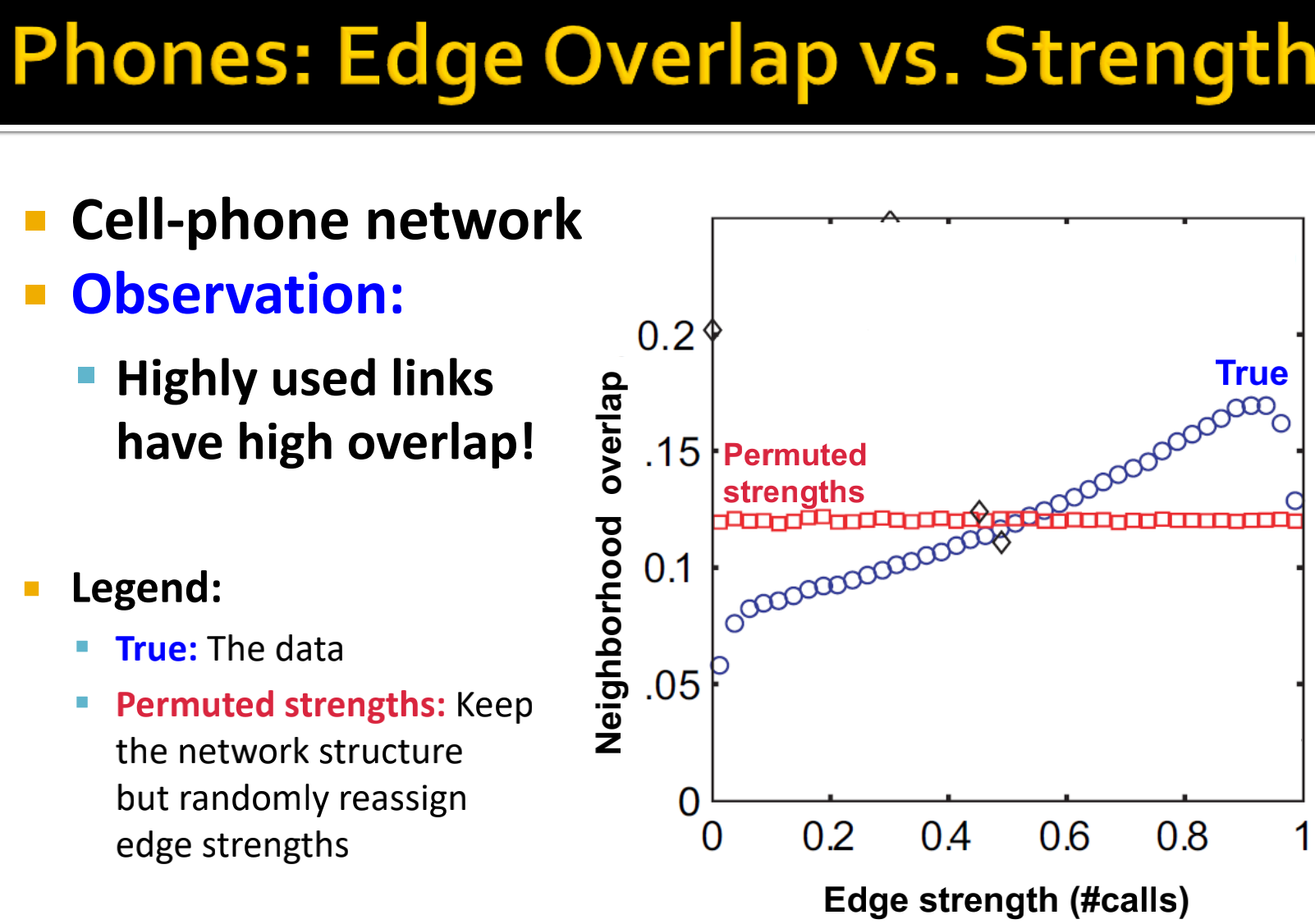
Edge Overlap:,其中
表示节点
的邻居集合。
Overlap=0表示一条边是局部bridge。
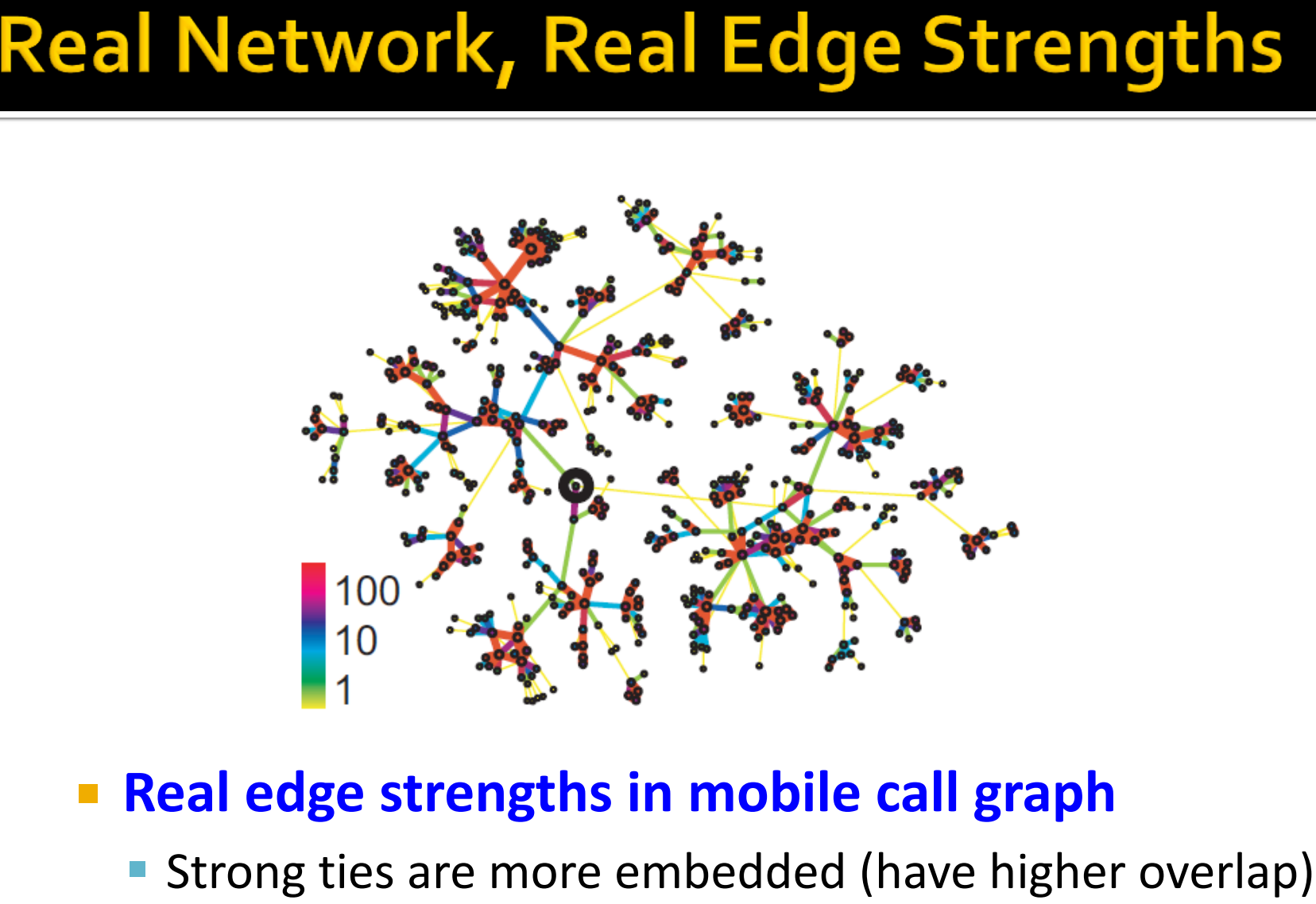

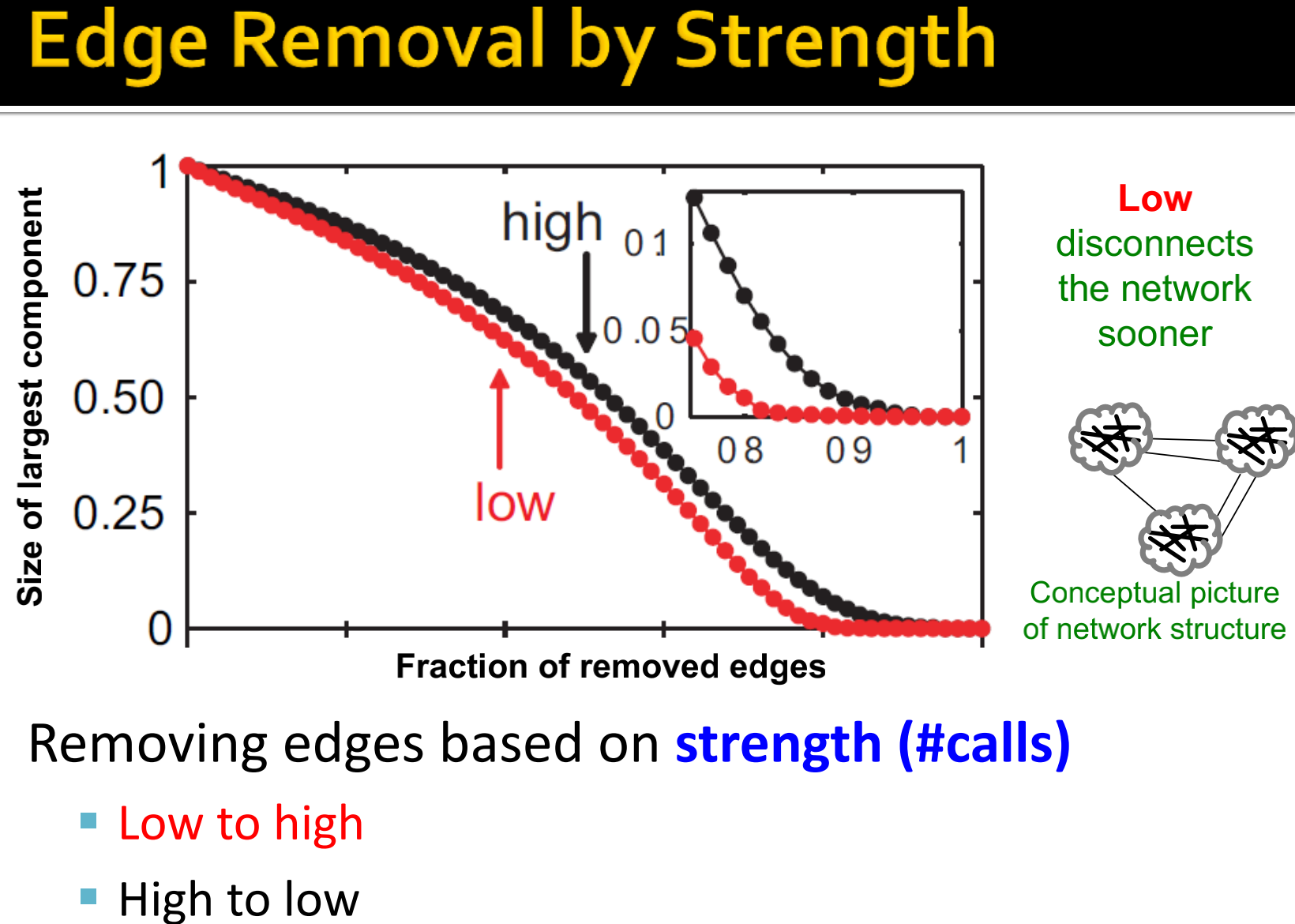
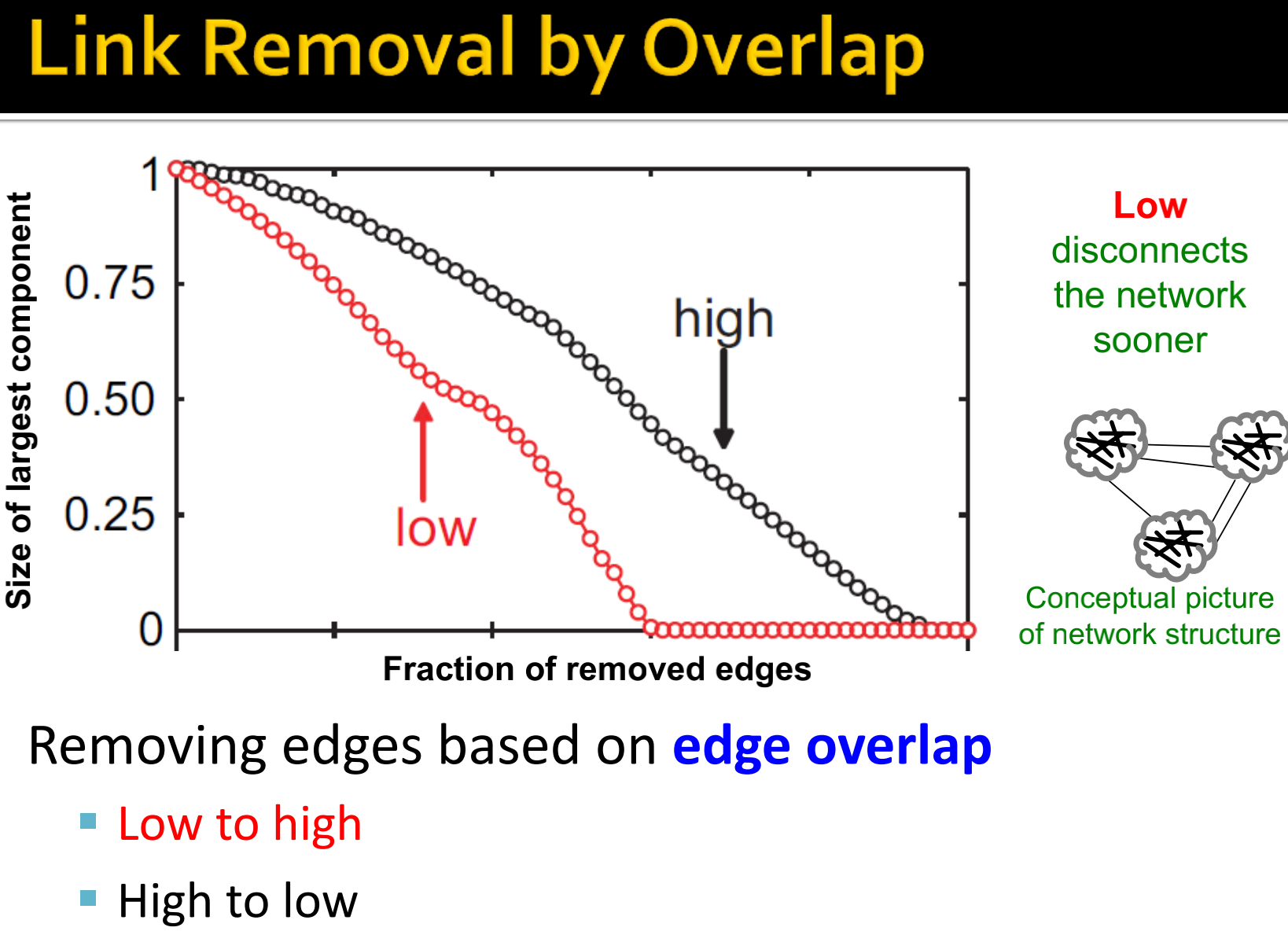
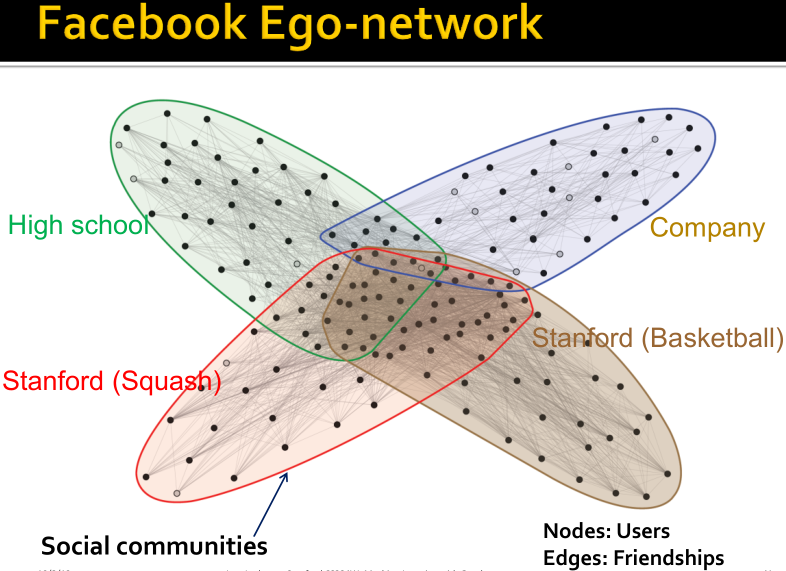
如下图所示,可以看作是三个社区,社区内部是强连接,社区之间弱连接。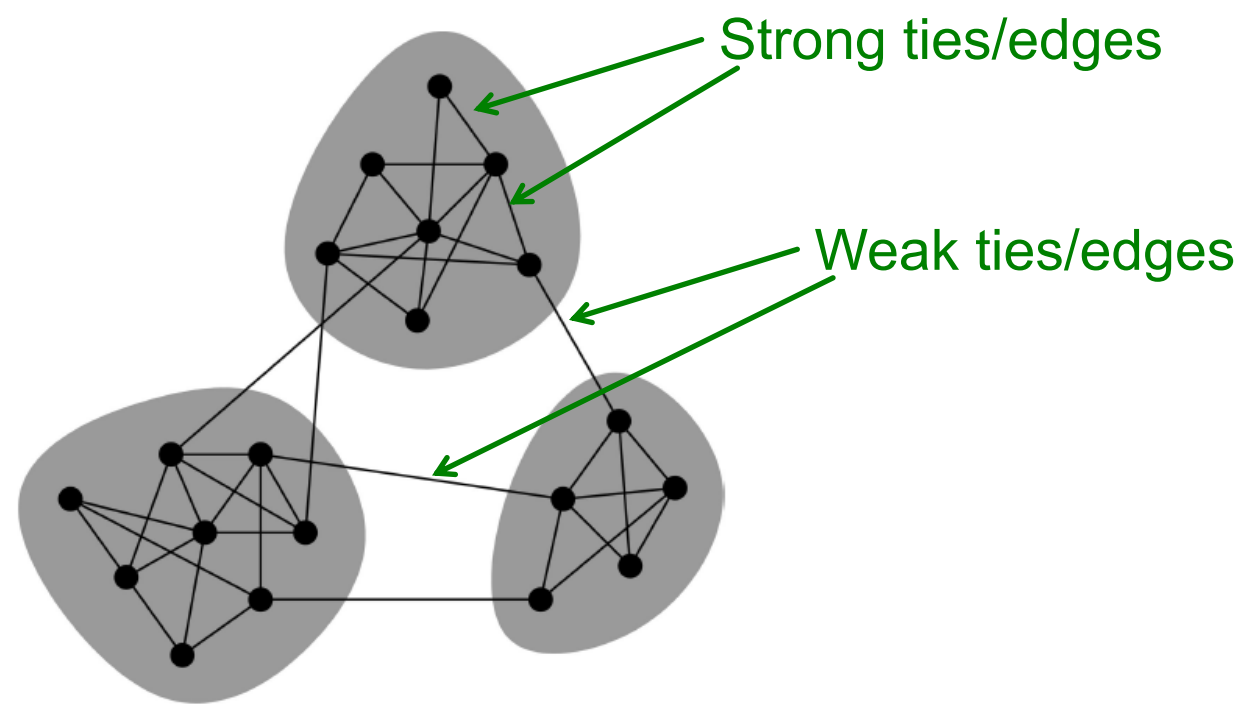
Communities: sets of tightly connected nodes
Modularity Q
Modularity Q:衡量网络划分成社区的效果。
给定网络的分区为不相干的分组,则
其中expected # edges within group s需要一个null model
Null Model
基于给定个节点和
条边的真实图
,创建网络
:
与
有相同的度分布,但是
中的边随机连接的;
- 考虑
是一个multigraph;
-
Modularity
modularity of partitioning S of graph G:
表示节点
和
之间边的权重;
表示与节点
相连的边的权重之和;
表示所有边权重之和;
表示节点
所属的社区;
- 当节点
和
属于同一个社区,即
,则
。
Modularity取值范围,若为正值则表示组间边数超出预期,Q值大于0.3~0.7意味着是显著的社区结构。
通过极大化modularity来区分社区。
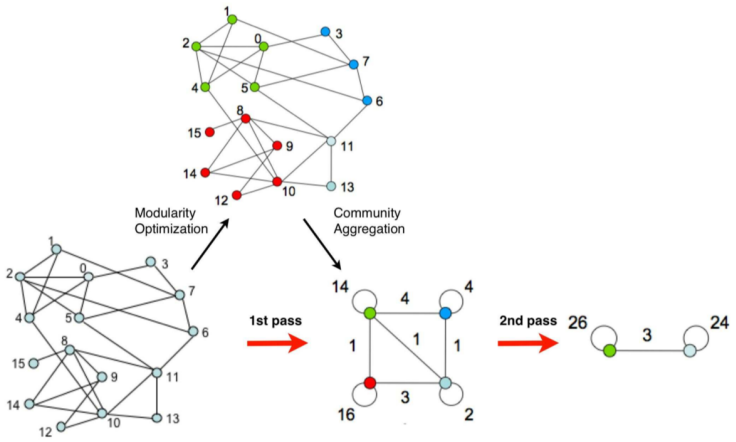
Louvain Algorithm
一种贪婪的社区检测方法,时间复杂度为,支持加权图,提供分层社区,由于该算法快速迭代聚合、有较高的Modularity输出,因此被广泛用来研究大网络。
hierarchical 阶层式;分层的;分等级的
Louvain算法贪婪地极大化Modularity,该算法由两个部分组成:
- phase1 为每个节点选择最优的社区,使局部模块度达到最大
- phase2 对划分好社区的网络进行重构
- 上述两个步骤不断迭代,直至Modularity不再发生变化
phase1 Partitioning
- 将图中每个节点都视为一个独特的社区(一个节点一个社区)。
- 对每个节点
,计算当把节点
放入一些邻居节点
所属社区时的
,将取得最大
所对应的节点
与邻居节点所属社区合并。
重复至
无变化。
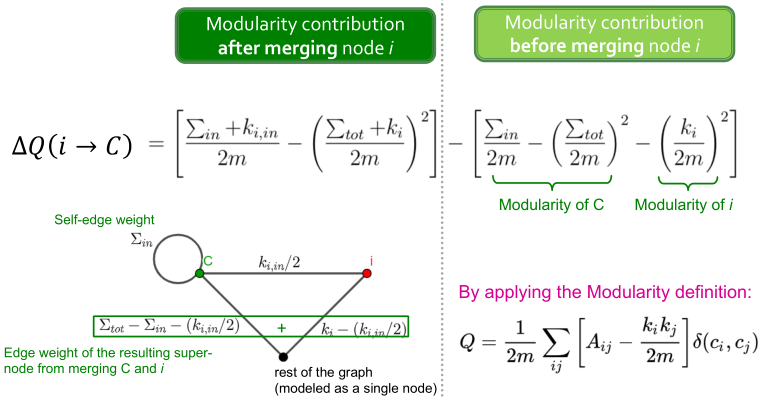
将节点
移至社区
时,
表示
中节点之间连接权重之和;
表示
中所有连接权重之和;
表示节点
和
之间所有连接权重之和;
表示节点
所有权重之和。
phase2 Restructuring
将phase1得到的communities定义为super-nodes。
- 若相关社区的节点之间至少有一个边,则super-nodes是连接的。
- 两个super-nodes的边权重是相关社区之间所有边权重之和。
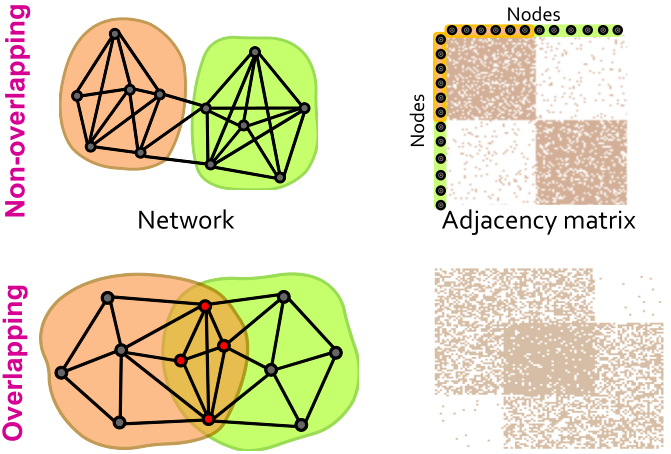
Detecting Overlapping Communities: BigCLAM
- step1 基于节点社区关系给图定义一个生成模型,Community Affiliation Graph Model (AGM)
- step2 给定图G,假设G是由AGM生成的
- step2 周到能生成G的最优的AGM
-
Community-Affiliation Graph Model (AGM)
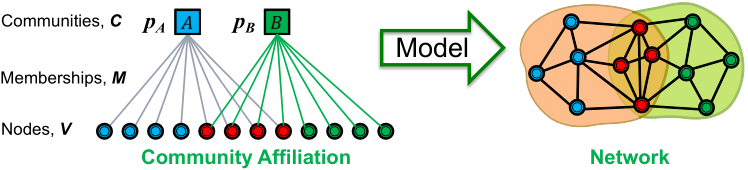
模型参数: 节点
,社区
,成员
- 每个社区
有个单独的概率
给定参数,社区
中的节点以概率
相连,节点属于多个社区的概率是多个社区概率相乘(If the miss the first time, they get another chance through the next community.)。
如,两个节点都在社区A和B中,那么这两个节点相连的概率为
两个节点在图中相连的概率为,若节点
和
没有共同的社区,则
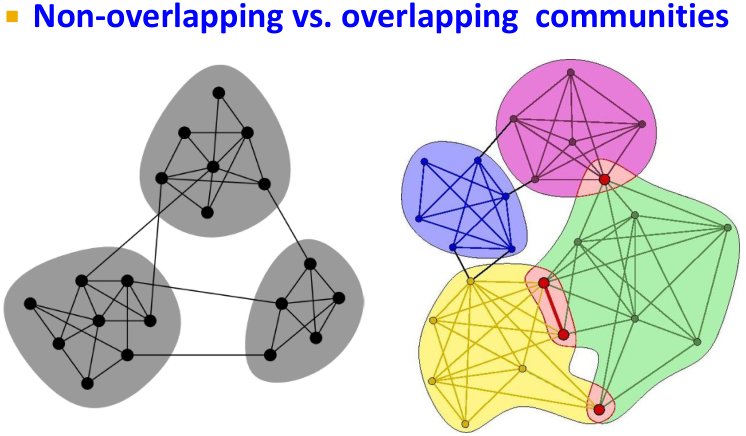
如果按照这种方法,AGM可以适用于多种图,如下图所示,重叠图、非重叠图、覆盖图利用上述AGM算法都可以生成同构图。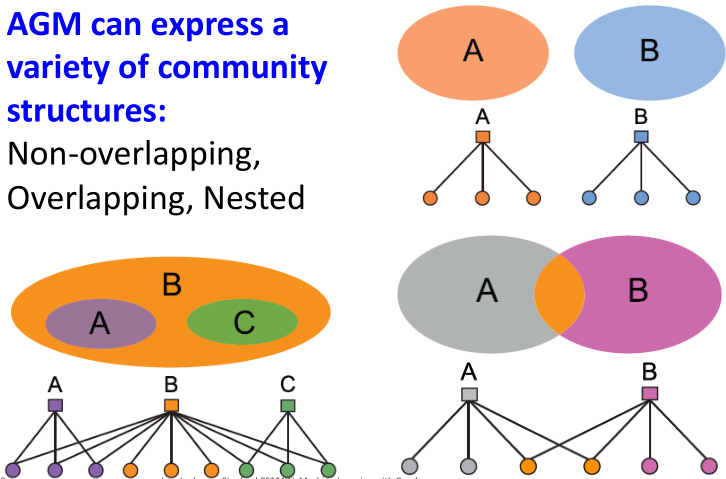
Detecting Communities with AGM
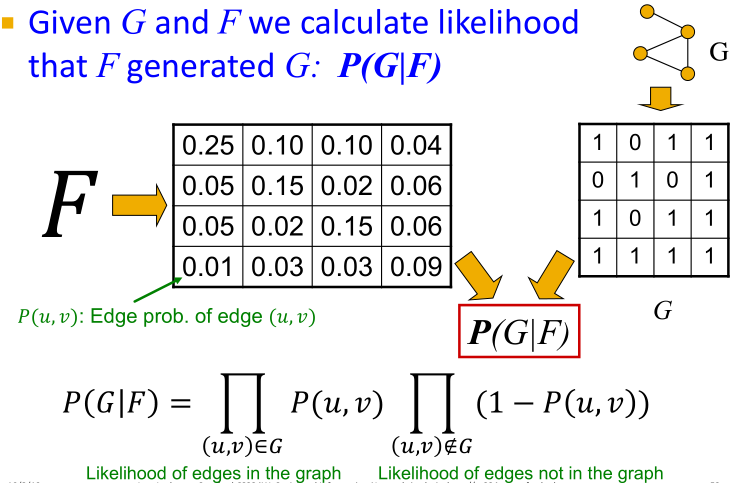
给定一个图,找到模型:
- Affiliation graph
- 社区
的数量
- 参数
如何基于给定图拟合模型
?
- 极大似然估计
- 给定真实图
- 找到模型/参数
使得
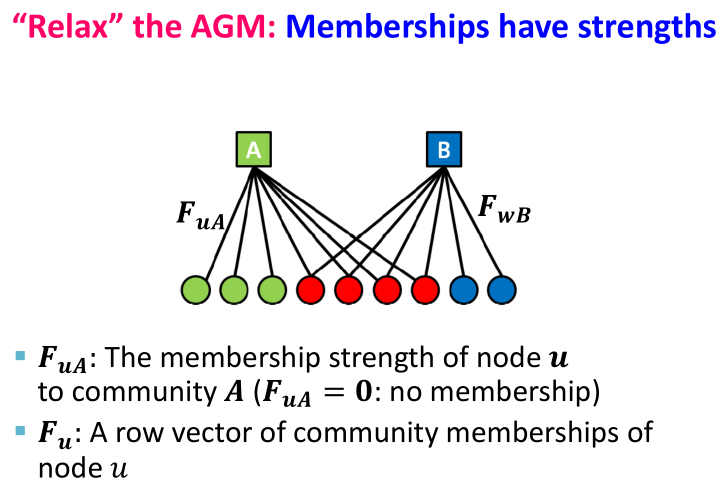
那BigCLAM是什么呢?它是AGM上的一种Relax,BigCLAM认为在二分图中,节点属于社区是有权重的,比如说我和A社区关系更紧密,权重大一点,和B社区关系一般,权重小一点,那么节点属于社区的权重越大,这个节点就越容易和其他节点相连。利用表示节点
和各个社区的权重向量,比如
表示节点
和社区
的权重,那么节点
和节点
有边相连的概率为:
给定一个网络,极大化
梯度下降:
关于AGM与BigCLAM的两篇文章:
Yang J , Leskovec J . Community-Affiliation Graph Model for Overlapping Network Community Detection[C]// IEEE International Conference on Data Mining. IEEE, 2012.
Yang J , Leskovec J . Overlapping community detection at scale: A nonnegative matrix factorization approach[C]// Proceedings of the sixth ACM international conference on Web search and data mining. ACM, 2013.
参考链接
知乎笔记:https://zhuanlan.zhihu.com/p/138824980
PPT:http://web.stanford.edu/class/cs224w/slides/04-communities.pdf