第二章：动态规划初探

第二章：动态规划初探

2.1 坐标型动态规划

最简单的动态规划类型
给定一个序列或网格
需要找到序列中某个/些子序列或网格中的某条路径
- 某种性质最大/最小
- 计数
- 存在性
动态规划方程f[i]中的下标i表示以为结尾的满足条件的子序列的性质，f[i][j]中的下标i``j表示以格子(i,j)为结尾的满足条件的路径的性质
- 最大值/最小值
- 个数
- 是否存在
坐标型动态规划的初始条件f[0]就是指以为结尾的子序列的性质

2.2 坐标型动态规划总结
给定输入为序列或者网格/矩阵
动态规划状态下标为序列下标i或者网格坐标(i,j)
- f[i]：以第i个元素结尾的某种性质
- f[i][j]：到格子(i,j)的路径的性质
初始化设置f[0]的值 / f[0][0...n-1]的值
二维空间优化：如果f[i][j]的值只依赖于当前行和前一行，则可以用滚动数组节省空间

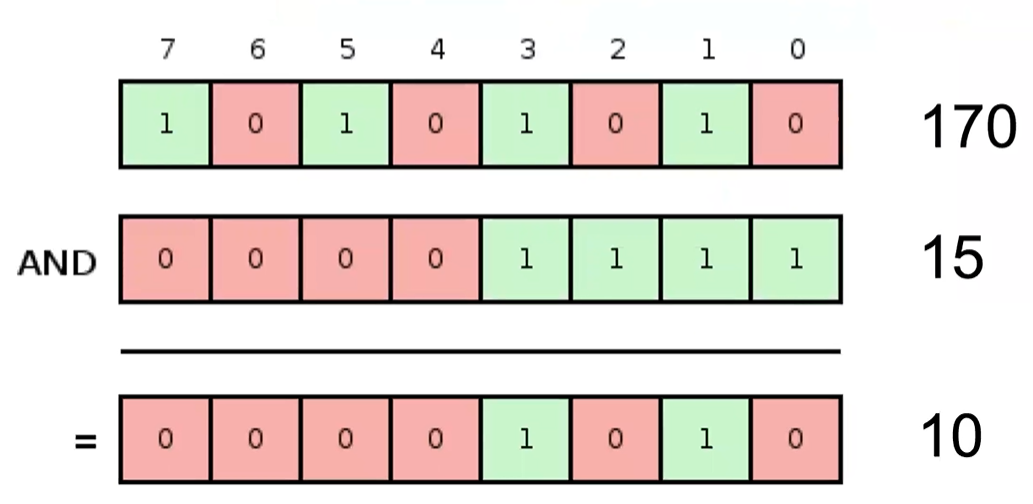
2.3 位操作型动态规划

位操作（二进制）
与 或 ``异或``非
& |``^``!
逐位操作

2.4 题目解析

115 · 不同的路径 II

解析

题意：

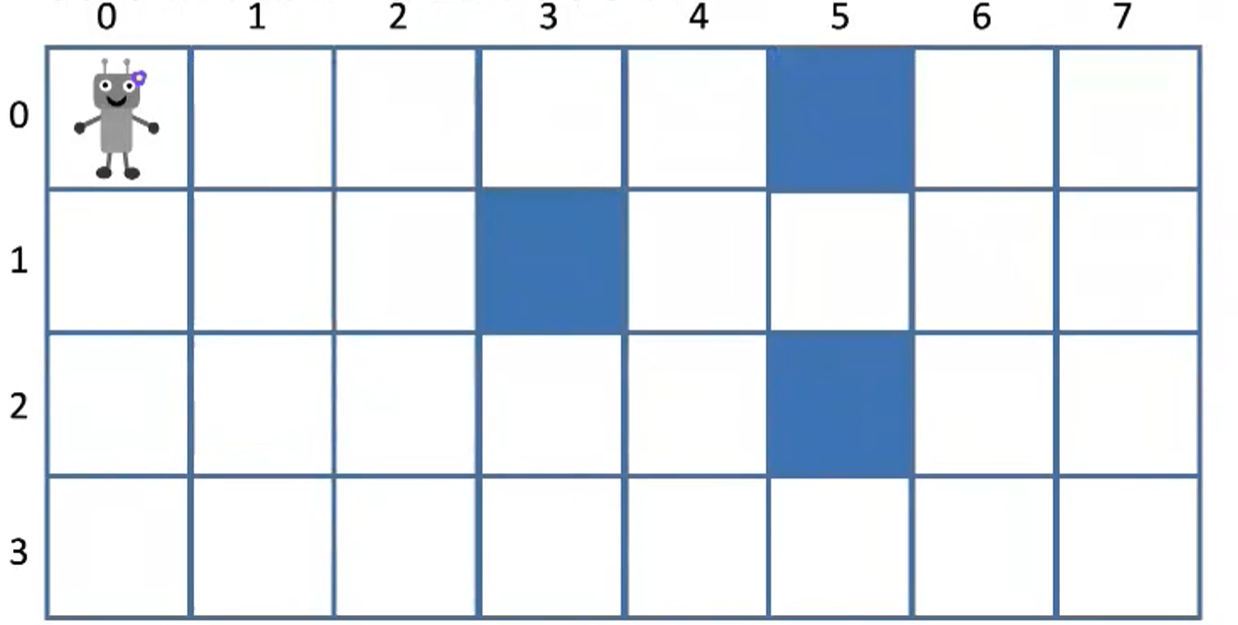
给定m行n列的网格，有一个机器人从左上角（0，0）出发，每一步可以向下或者向右走一步
网格中有些地方有障碍，机器人不能通过障碍格子
问有多少种不同的方式走到右下角

题目分析：

这题和Unique Path 非常类似，只是网格中可能有障碍
最后一步一定是从左边(i,j-1)或上边(i-1,j)过来
状态f[i][j]表示从左上角有多少种方式走到格子(i,j)
坐标型动态规划：数组下表[i][j]即坐标(i,j)

初始条件和边界情况：

f[i][j] = 机器人有多少种方式从左上角走到(i,j)
如果左上角(0,0)格或者右下角(m-1,n-1)格有障碍，直接输出0
如果(i,j)格有障碍，f[i][j] = 0，表示机器人不能到达此格(0种方式)
初始条件：f[0][0] = 1

第二章：动态规划初探 - 图7

题目

:::info “不同的路径“ 的跟进问题：
有一个机器人的位于一个 m × n 个网格左上角。
机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。
现在考虑网格中有障碍物，那样将会有多少条不同的路径？
网格中的障碍和空位置分别用 1 和 0 来表示。 :::

👋 %22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%22778%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6E%22%20x%3D%221834%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2264%22%20x%3D%222712%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(3769%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%22500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-30%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=1%5Cleq%20n%20%5Cleq%20100&id=nNULy)

样例

Input:

obstacleGrid = [[0]]

Output: :::success 1 ::: Explain: :::warning 只有一个点 :::

Input:

obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]

Output: :::success 2 ::: Explain: :::warning 只有 2 种不同的路径 :::

代码

DP

func UniquePathsWithObstacles(a [][]int) int {
    // write your code here
    if a == nil || len(a) == 0 || len(a[0]) == 0 {
        return 0
    }
    m, n := len(a), len(a[0])
    f := make([][]int, m)
    for i := 0; i < m; i++ {
        f[i] = make([]int, n)
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if a[i][j] == 1 {
                //obstacle
                f[i][j] = 0
                continue
            }
            if i == 0 && j == 0 {
                f[i][j] = 1
                continue
            }
            f[i][j] = 0
            if i > 0 {
                f[i][j] += f[i-1][j]
            }
            if j > 0 {
                f[i][j] += f[i][j-1]
            }
        }
    }
    return f[m-1][n-1]
}

515 · 房屋染色

解析

题意：

有一排N栋房子，每栋房子要漆成3种颜色中的一种：红、蓝、绿
任何两栋相邻的房子不能漆成同样的颜色
第i栋房子染成红、蓝、绿色的花费分别是cost[i][0]、cost[i][1]、cost[i][2]
问最少需要花多少钱油漆这些房子

确定状态：

最优策略是花费最小的策略
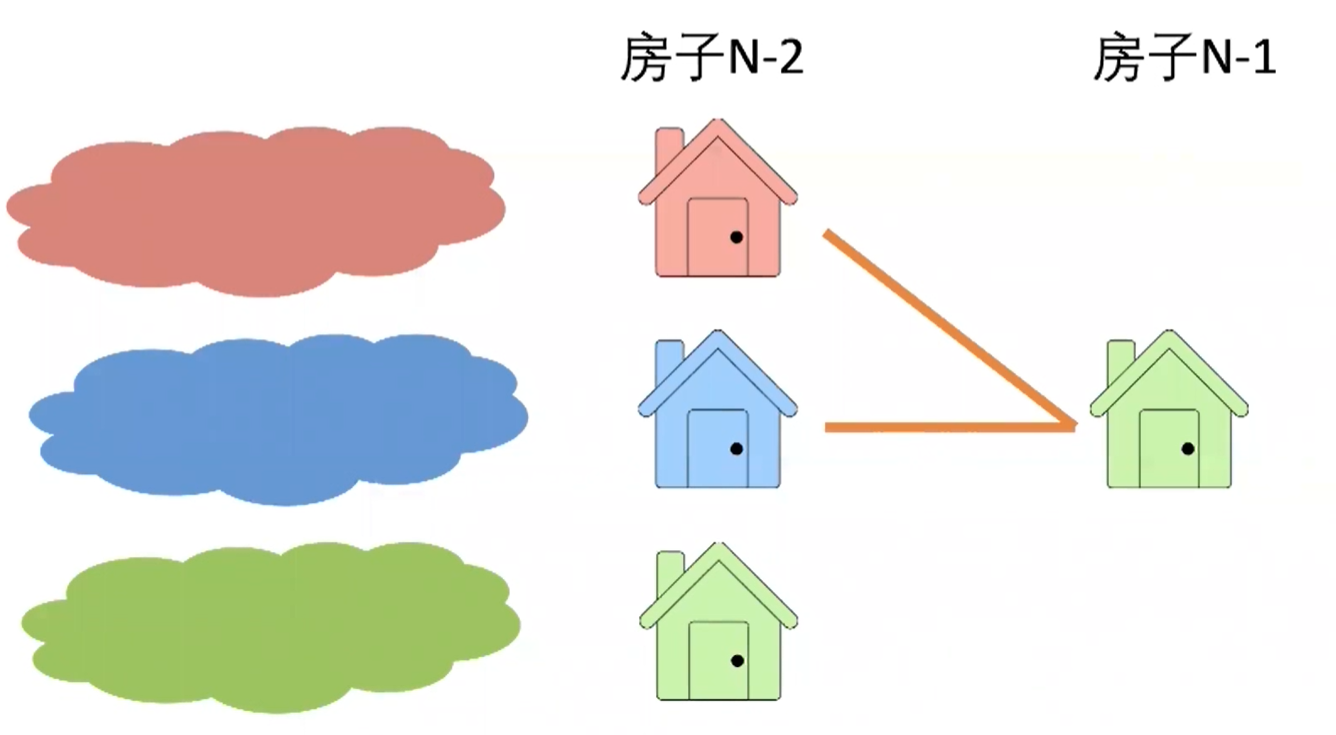
最后一步：最优策略中房子N-1一定染成了红蓝绿中的一种
但是相邻的两栋房子不能漆成一种颜色
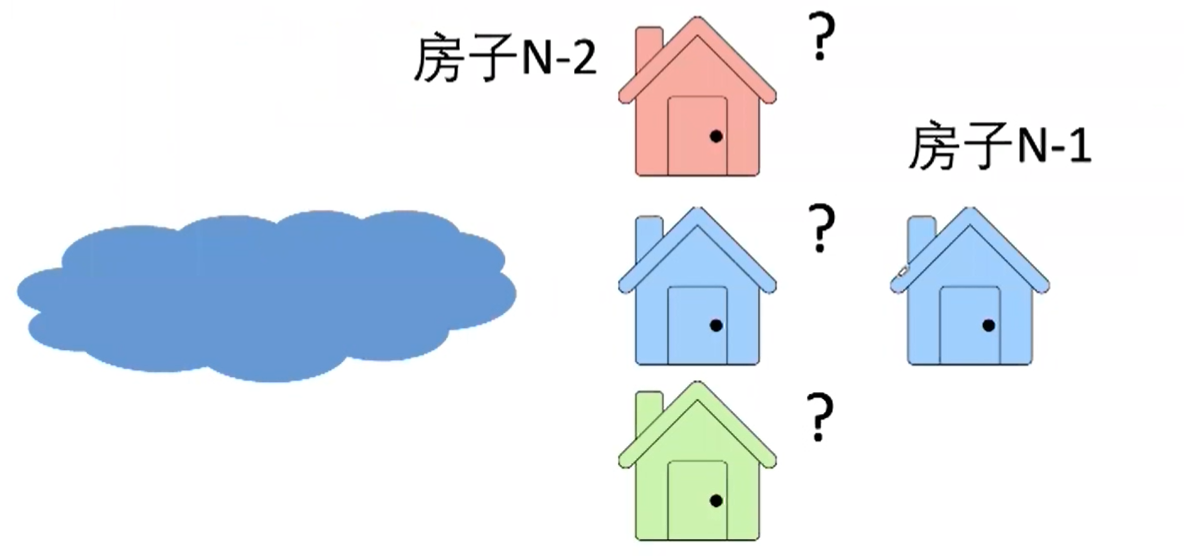
所以如果最优策略中房子N-1是红色，则房子N-2只能是蓝色或绿色
所以如果最优策略中房子N-1是蓝色，则房子N-2只能是红色或绿色
所以如果最优策略中房子N-1是绿色，则房子N-2只能是红色或蓝色
如果直接套用以前的思路，记录油漆前N栋房子的最小花费
根据套路，也需要记录油漆前N-1栋房子的最小花费
但是，前N-1栋房子的最小花费的最优策略中，不知道房子N-2是什么颜色，所以有可能和房子N-1撞色
不知道房子N-2是什么颜色，就把它记录下来！
分别记录油漆前N-1栋房子并且房子N-2是红、蓝、绿三色中的最小花费

子问题：

求油漆前N栋房子并且房子N-1是红、蓝、绿三色中的最小花费
需要知道油漆前N-1栋房子并且房子N-2是红、蓝、绿三色的最小花费
子问题
状态：设油漆前i栋房子并且房子i-1是红、蓝、绿三色的最小花费分别为f[i][0] f[i][1] f[i][2]

转移方程：

设油漆前i栋房子并且房子i-1是红、蓝、绿三色的最小花费分别为f[i][0] f[i][1] f[i][2]

初始条件和边界情况：

初始条件：f[0][0] = f[0][1] = f[0][2] = 0

即不油漆任何房子的花费

无边界情况

计算顺序：

初始化f[0][0] = f[0][1] = f[0][2]
计算f[1][0] f[1][1] f[1][2]
...
计算f[N][0] f[N][1] f[N][2]
答案是min{f[N][0] f[N][1] f[N][2]}
时间复杂度：
空间复杂度：

题目

:::info 这里有n个房子在一列直线上，现在我们需要给房屋染色，分别有红、蓝、绿三色。每个房屋染不同的颜色费用也不同，你需要设计一种染色方案使得相邻的房屋颜色不同，并且费用最小，返回最小的费用。
费用通过一个nx3 的矩阵给出，比如cost[0][0]表示房屋0染红色的费用，cost[1][2]表示房屋1染绿色的费用，依此类推。找到油漆所有房子的最低成本。 :::

👋 所有费用都是正整数

样例

Input:

[[14,2,11],[11,14,5],[14,3,10]]

Output: :::success 10 ::: Explain: :::warning 第一个屋子染蓝色，第二个染绿色，第三个染蓝色，最小花费：2 + 5 + 3 = 10. :::

Input:

[[1,2,3],[1,4,6]]

Output: :::success 3 ::: Explain: :::warning 第一个屋子染蓝色，第二个染红色，最小花费：2 + 1 = 3. :::

代码

坐标型DP

import "math"
func MinCost(costs [][]int) int {
    // write your code here
    n := len(costs)
    if n == 0 {
        return 0
    }
    f := make([][]int, n+1)
    //序列型
    for i := 0; i < n+1; i++ {
        f[i] = make([]int, 3)
    }
    //初始状态
    f[0][0], f[0][1], f[0][2] = 0, 0, 0
    //前 i 栋 房子
    for i := 1; i <= n; i++ {
        for j := 0; j < 3; j++ {
            f[i][j] = math.MaxInt
            for k := 0; k < 3; k++ {
                //不能撞色
                if j == k {
                    continue
                }
                f[i][j] = min(f[i][j], f[i-1][k]+costs[i-1][j])
            }
        }
    }
    return min(f[n][0], min(f[n][1], f[n][2]))
}
func min(x, y int) int {
    if x > y {
        return y
    }
    return x
}

小结

序列型动态规划：前**i**个最小/方式数/可行性
在设计动态规划的过程中，发现需要知道油漆前N-1栋房子的最优策略中，房子N-2的颜色
如果只用f[N-1]，将无法区分
解决方法：记录下房子N-2的颜色
- 在房子N-2是红 / 蓝 / 绿色的情况下，油漆前N-1栋房子的最小花费
问题迎刃而解
序列+状态
512 · 解码方法
解析
题意：
- 有一段由A-Z组成的字母串信息被加密成数字串
- 加密方式：A->1 B->2 ... Z->26
- 给定加密后的数字串S[0...N-1]，问有多少种方式解密成字母串

确定状态：

解密数字串即划分成若干段数字，每段数字对应一个字母
最后一步（最后一段）：对应一个字母

A B ... Z

这个字母加密时变成1 2 ... 26

子问题：

设数字串长度为N
要求数字串前N个字符的解密方式数
需要知道数字串前N-1和N-2个字符的解密方式数
子问题
状态：设数字串S前i个数字解密成字母串有f[i]种方式

转移方程：

设数字串S前i个数字解密成字母串有f[i]种方式

初始条件和边界情况：

设数字串S前i个数字解密成字母串有f[i]种方式
初始条件：f[0] = 1，即空串有1种方式解密

解密成空串

边界情况：如果i=1，只看最后一个数字

计算顺序：

f[0] f[1] ... f[N]
答案是f[N]
时间复杂度
空间复杂度

题目

:::info 有一个消息包含A-Z通过以下规则编码 :::

‘A’ -> 1 ‘B’ -> 2 … ‘Z’ -> 26

:::info 现在给你一个加密过后的消息，问有几种解码的方式 :::

👋 我们不能解码空串，因此若消息为空，你应该返回0。
消息的长度

样例

Input:

“12”

Output: :::success 2 ::: Explain: :::warning 它可以被解码为 AB (1 2) 或 L (12). :::

Input:

“10”

Output: :::success 1 ::: Explain: :::warning 0不归属于A-Z，故只有10一种解码方式 :::

代码

func NumDecodings(s string) int {
    // write your code here
    str := []byte(s)
    n := len(str)
    if n == 0 {
        return 0
    }
    f := make([]int, n+1)
    f[0] = 1
    for i := 1; i <= n; i++ {
        f[i] = 0
        //最后一位
        if str[i-1] != '0' {
            f[i] += f[i-1]
        }
        //最后两位
        if i >= 2 && (str[i-2] == '1' || (str[i-2] == '2' && s[i-1] <= '6')) {
            f[i] += f[i-2]
        }
    }
    return f[n]
}

110 · 最小路径和

解析

题意：

给定m行n列的网格，每个格子(i,j)里都有一个非负数A[i][j]
求一个从左上角(0,0)到右下角的路径，每一步只能向下或者向右走一步
使得路径上的格子里的数字之和最小
输出最小数字和

确定状态：

最值型动态规划
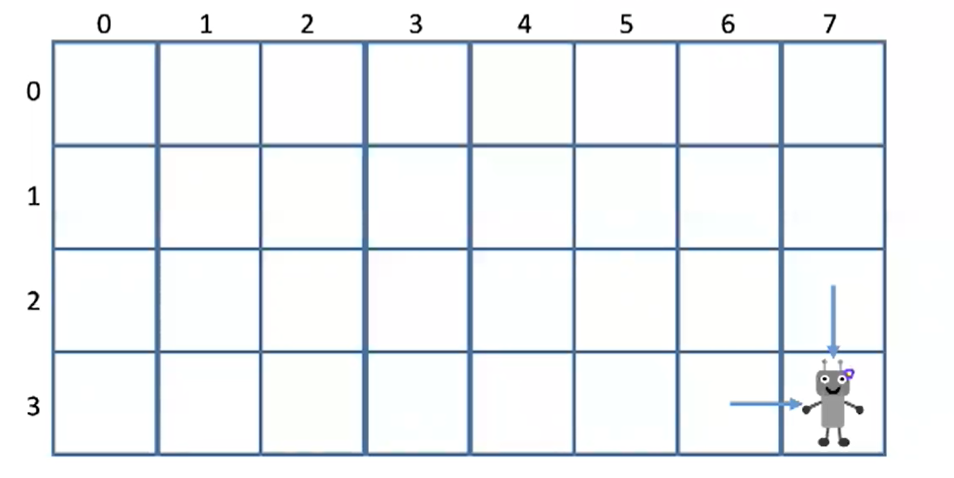
和Unique Path一样，无论用何种方式到达右下角，总有最后一步：

向右或者向下

右下角坐标设为(m-1,n-1)
那么，前一步一定是在(m-2,n-1)或者(m-1,n-2)
最优策略的路径总和数字最小

若倒数第二步在(m-2,n-1)，则前面一定是从(0,0)到达(m-2,n-1)总和最小的路径
若倒数第二步在(m-1,n-2)，则前面一定是从(0,0)到达(m-1,n-2)总和最小的路径

子问题：

要求从左上角走到(m-1,n-2)的路径的最小数字总和以及走到(m-2,n-1)的路径的最小数字总和
原题要求有从左上角走到(m-1,n-1)的路径的最小数字总和
子问题
状态：

设从(0,0)走到(i,j)的路径最小数字总和f[i][j]

转移方程：

设从(0,0)走到(i,j)的路径最小数字总和f[i][j]

初始条件和边界情况：

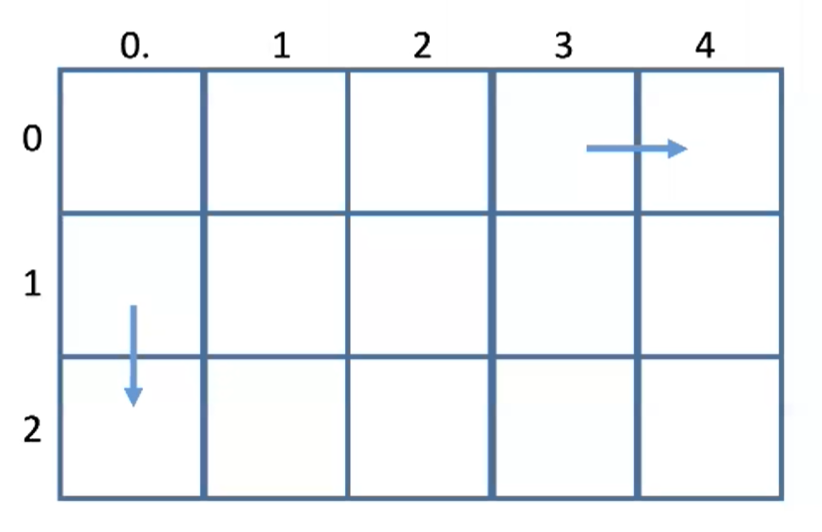
初始条件：f[0][0] = A[0][0]
边界情况：i=0或j=0，则前一步只能有一个方向过来

计算顺序：

f[0][0] = A[0][0]
计算第0行：f[0][0] f[0][1] ... f[0][n-1]
计算第1行：f[1][0] f[1][1] ... f[1][n-1]
...
计算第m-1行：f[m-1][0] f[m-1][1] ... f[m-1][n-1]
f[i][j] = min{f[i-1][j],f[i][j-1]} + A[i][j]
时间复杂度：
空间复杂度（数组大小）：

题目

:::info 给定一个只含非负整数的m*n网格，找到一条从左上角到右下角的可以使数字和最小的路径。 :::

👋 你在同一时间只能向下或者向右移动一步

样例

Input:

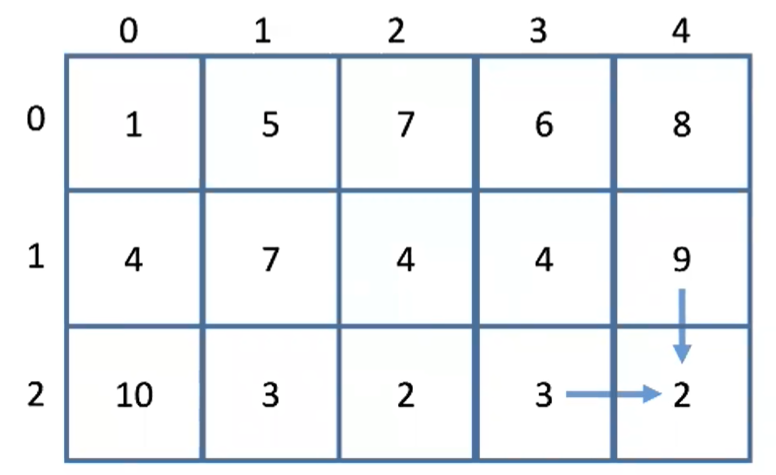
grid = [[1,3,1],[1,5,1],[4,2,1]]

Output: :::success 7 ::: Explain: :::warning 路线为： 1 -> 3 -> 1 -> 1 -> 1 :::

Input:

grid = [[1,3,2]]

Output: :::success 6 ::: Explain: :::warning 路线是： 1 -> 3 -> 2 :::

代码

序列型DP

import "math"
func MinPathSum(grid [][]int) int {
    // write your code here
    m, n := len(grid), len(grid[0])
    if grid == nil || m == 0 || n == 0 {
        return 0
    }
    f := make([][]int, m)
    for i := 0; i < m; i++ {
        f[i] = make([]int, n)
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if i == 0 && j == 0 {
                f[i][j] = grid[i][j]
                continue
            }
            f[i][j] = math.MaxInt
            if i > 0 {
                f[i][j] = min(f[i][j], f[i-1][j]+grid[i][j])
            }
            if j > 0 {
                f[i][j] = min(f[i][j], f[i][j-1]+grid[i][j])
            }
        }
    }
    return f[m-1][n-1]
}
func min(x, y int) int {
    if x > y {
        return y
    }
    return x
}

空间优化

f[i][j] = min{f[i-1][j],f[i][j-1]} + A[i][j]
计算第i行时，只需要第i行和第i-1行的f
所以，只需要保存两行的f值，f[i][0...n-1]和f[i-1][0...n-1]
用滚动数组实现

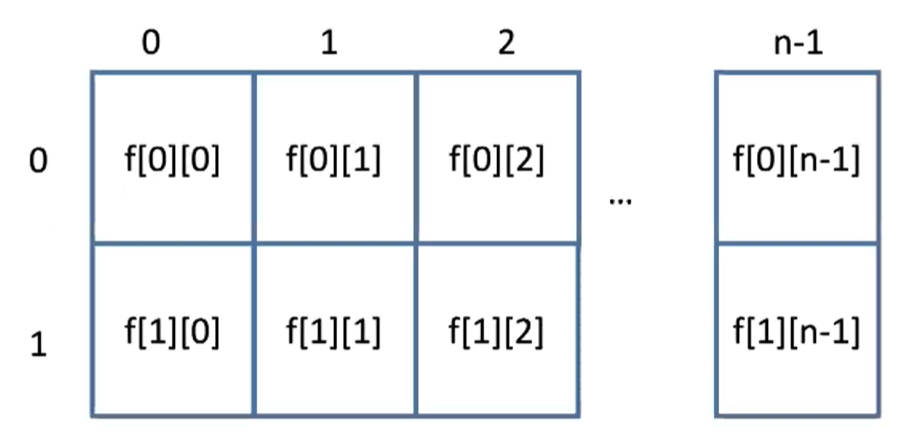
开数组时，只开f[0][0...n-1]和f[1][0...n-1]
计算f[0][0] ... f[0][n-1]和f[1][0] ... f[1][n-1]
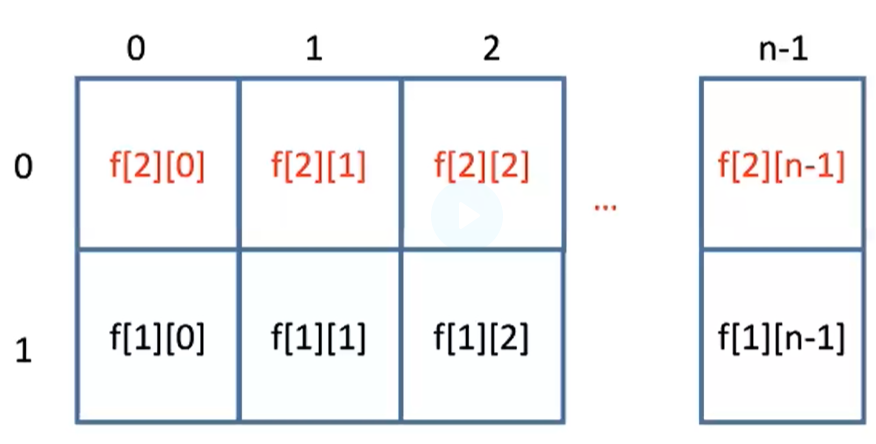
计算f[2][0...n-1]时，开f[2][0...n-1]，删掉f[0][0...n-1]，因为已经不需要f[0][0...n-1]的值了
计算f[3][0...n-1]时，开f[3][0...n-1]，删掉f[1][0...n-1]，因为已经不需要f[1][0...n-1]的值了
实际操作时，可以不用每次开数组，而是用滚动法
计算f[0][0] ... f[0][n-1]计算f[1][0] ... f[1][n-1]
计算f[2][0]时,把值写在f[0][0...n-1]的数组里
同理，f[3][0...n-1]写在f[1][0...n-1]的数组里
最后f[m-1][n-1]存储在f[0][n-1]（或者f[1][n-1]）里，直接输出

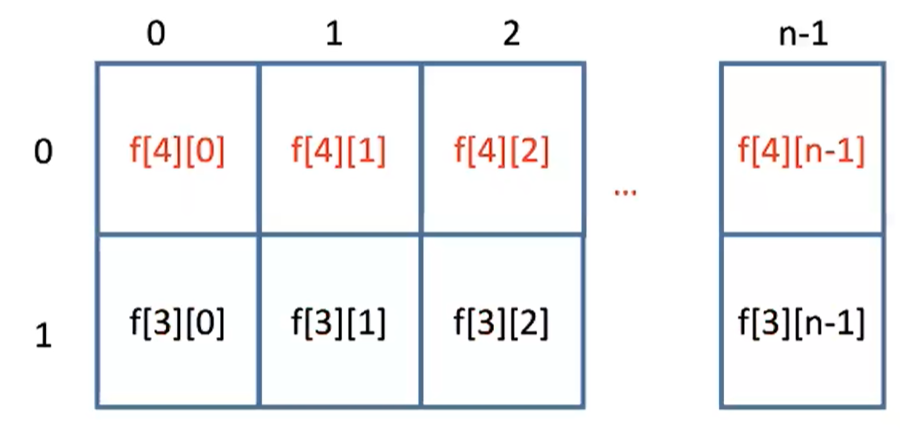
知识点：对于网格上的动态规划，如果f[i][j]只依赖于本行的f[i][x]与前一行的f[i-1][y]，那么，就可以采用滚动数组的方法压缩空间。空间复杂度：O(N)

知识点：如果网格行数少列数多（大胖子网格），那么，就可以逐列计算，滚动数组的长度为行数，空间复杂度：O(M)

553 · 炸弹袭击

解析

题意：

有一个M*N的网格，每个格子可能是空的，可能有一个敌人，可能有一堵墙
只能在某个空格子里放一个炸弹，炸弹会炸死所有同行同列的敌人，但是不能穿透墙
最多炸死几个敌人
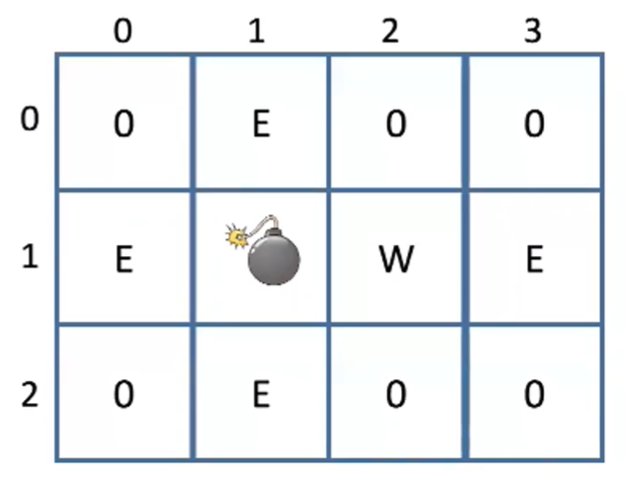
例子：
输入：如图
输出：3

题目分析：

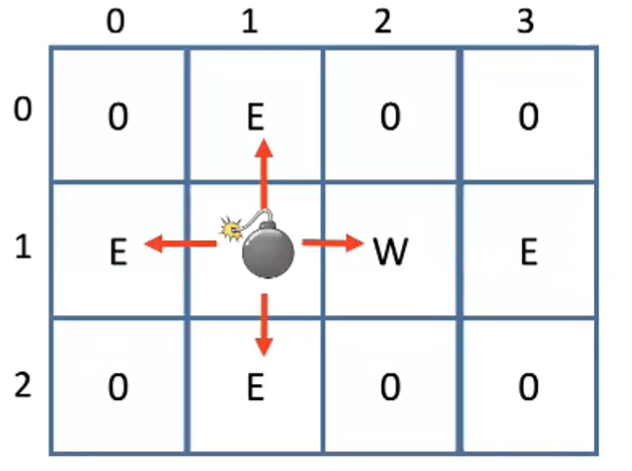
每个炸弹可以往四个方向传播爆炸力
我们可以分析一个方向，然后举一反三
即如果在一个空地放一个炸弹，最多向上能炸死多少敌人
可以直接枚举，即向上枚举到碰到墙为止
时间复杂度：
用动态规划思想加速

确定状态：

我们假设有敌人或有墙的格子也能放炸弹

有敌人的格子：格子里的敌人被炸死，并继续向上爆炸
有墙的格子：炸弹不能炸死任何敌人

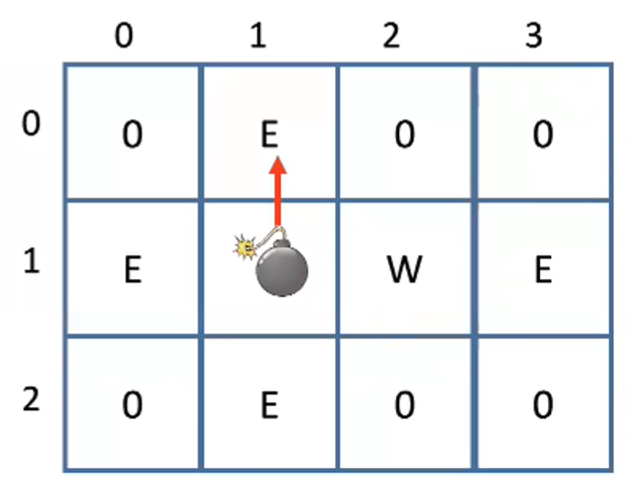
在(i,j)格放一个炸弹，它向上能炸死的敌人数是：

(i,j)格为空地：(i-1,j)格向上能炸死的敌人数
(i,j)格为敌人：(i-1,j)格向上能炸死的敌人数 + 1
(i,j)格为墙：0

子问题：

需要知道(i-1,j)格放一个炸弹向上能炸死的敌人数
原来要求(i,j)格放一个炸弹向上能炸死的敌人数
子问题
状态：Up[i][j]表示(i,j)格放一个炸弹向上能炸死的敌人数

转移方程：

设Up[i][j]表示(i,j)格放一个炸弹向上能炸死的敌人数

第二章：动态规划初探 - 图40

初始条件和边界情况：

第0行的Up值和格子内容相关

Up[0][j] = 0，如果(0,j)格不是敌人
Up[0][j] = 1，如果(0,j)格是敌人

计算顺序：

逐行计算
Up[0][0] Up[0][1] ... Up[0][n-1]
...
Up[m-1][0] Up[m-1][1] ... Up[m-1][n-1]
时间复杂度：
空间复杂度：

四个方向：

Up[i][j]表示如果(i,j)放一个炸弹向上可以最多炸死多少敌人
一共四个方向
可以类似地计算Down[i][j] Left[i][j] Right[i][j]，注意计算顺序会有改变
(i,j)如果是空地，放一个炸弹最多炸死的敌人数是：

Up[i][j] + Down[i][j] + Left[i][j] + Right[i][j]

取最大值即可
时空复杂度依旧为：

题目

:::info 给定一个二维矩阵, 每一个格子可能是一堵墙 W,或者一个敌人 E 或者空 0 (数字 ‘0’), 返回你可以用一个炸弹杀死的最大敌人数. 炸弹会杀死所有在同一行和同一列没有墙阻隔的敌人。由于墙比较坚固，所以墙不会被摧毁. :::

👋 你只能在空的地方放置炸弹.

样例

Input:

grid =[ “0E00”, “E0WE”, “0E00” ]

Output: :::success 3 ::: Explain: :::warning 把炸弹放在 (1,1) 能杀3个敌人 :::

Input:

grid =[ “0E00”, “EEWE”, “0E00”]

Output: :::success 2 ::: Explain: :::warning P把炸弹放在 (0,0) 或 (0,3) 或 (2,0) 或 (2,3) 能杀2个敌人 :::

代码

func MaxKilledEnemies(grid [][]byte) int {
    // write your code here
    //corner case
    if grid == nil || len(grid) == 0 || len(grid[0]) == 0 {
        return 0
    }
    m, n := len(grid), len(grid[0])
    //初始化 上下左右四个数组
    up := make([][]int, m)
    for i := 0; i < m; i++ {
        up[i] = make([]int, n)
    }
    down := make([][]int, m)
    for i := 0; i < m; i++ {
        down[i] = make([]int, n)
    }
    left := make([][]int, m)
    for i := 0; i < m; i++ {
        left[i] = make([]int, n)
    }
    right := make([][]int, m)
    for i := 0; i < m; i++ {
        right[i] = make([]int, n)
    }
    //up
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] != 'W' {
                if grid[i][j] == 'E' {
                    up[i][j]++
                }
                if i > 0 {
                    up[i][j] += up[i-1][j]
                }
            }
        }
    }
    //down
    for i := m - 1; i >= 0; i-- {
        for j := 0; j < n; j++ {
            if grid[i][j] != 'W' {
                if grid[i][j] == 'E' {
                    down[i][j]++
                }
                if i < m-1 {
                    down[i][j] += down[i+1][j]
                }
            }
        }
    }
    //left
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] != 'W' {
                if grid[i][j] == 'E' {
                    left[i][j]++
                }
                if j > 0 {
                    left[i][j] += left[i][j-1]
                }
            }
        }
    }
    //right
    for i := 0; i < m; i++ {
        for j := n - 1; j >= 0; j-- {
            if grid[i][j] != 'W' {
                if grid[i][j] == 'E' {
                    right[i][j]++
                }
                if j < n-1 {
                    right[i][j] += right[i][j+1]
                }
            }
        }
    }
    res := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == '0' { //empty
                res = max(res, up[i][j]+down[i][j]+left[i][j]+right[i][j])
            }
        }
    }
    return res
}
func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

664 · 数 1

解析

题意：

给定N，要求输出0 1 ... N的每个数的二进制表示里1的个数

题目分析：

对于每个数0<=i<=N，直接求i的二进制表示里有多少个1
二进制表示算法

第一步：i mod 2是最低位的bit
第二步：i <- floor(i/2)，如果i=0，结束，否则回到第一步

时间复杂度：

2个数有1位二进制
2个数有2位二进制
4个数有3位二进制
8个数有4位二进制
...
大约N/2个数有位二进制

确定状态：

观察最后一个数的二进制位：

最后一步：观察这个数最后一个二进制位（最低位），去掉它，看剩下多少个1

85的二进制表示里有4个1
170的二进制表示里有4个1

子问题：

要求N的二进制表示中有多少1
在N的二进制去掉最后一位N mod 2，设新的数是Y = (N >> 1)``(右移一位)
要知道Y的二进制表示中有多少1
子问题
状态：设f[i]表示i的二进制表示中有多少个1

知识点：和位操作相关的动态规划一般用值作状态

转移方程：

设f[i]表示i的二进制表示中有多少个1

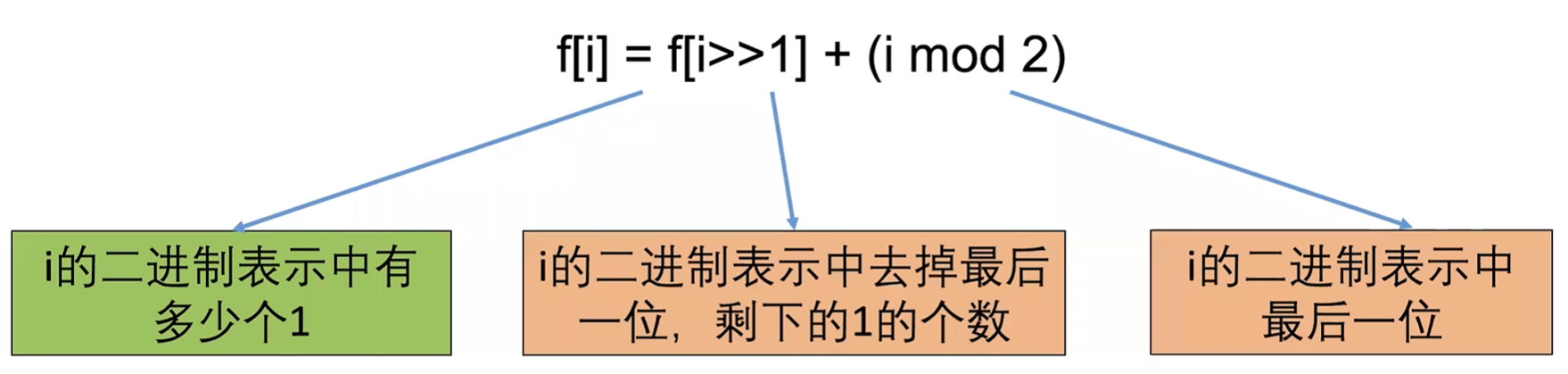
初始条件和边界情况：

设f[i]表示i的二进制表示中有多少个1
f[i] = f[i >> 1] + (i mod 2)
初始条件： f[0] = 0

计算顺序：

f[0] f[1] f[2] ... f[N]
时间复杂度：
空间复杂度：

题目

:::info

:::

👋

样例

Input:

Output: :::success

::: Explain: :::warning

:::

Input:

Output: :::success

::: Explain: :::warning

:::

代码

func CountBits(num int) []int {
    // write your code here
    f := make([]int, num+1)
    for i := 1; i <= num; i++ {
        f[i] = f[i>>1] + (i % 2)
    }
    return f
}

76 · 最长上升子序列

题目

:::info

:::

👋

样例

Input:

Output: :::success

::: Explain: :::warning

:::

Input:

Output: :::success

::: Explain: :::warning

:::

第二章：动态规划初探

第二章：动态规划初探

2.1 坐标型动态规划

2.2 坐标型动态规划总结

2.3 位操作型动态规划

2.4 题目解析

解析

题目

样例

代码

解析

题目

样例

代码

小结

解析

题目

样例

代码

解析

题目

样例

代码

空间优化

解析

题目

样例

代码

解析

题目

样例

代码

题目

样例

代码