第一章:动态规划入门
1.1 什么是动态规划
- 科技公司面试必考算法
- 题目类型多,没有固定模板
- 难度属于中上
- 根据面试经验,一半的失败都与动态规划有关
- 必须掌握
- 并没有那么可怕
- 有规律可循
- 掌握其中思想,举一反三
- 计数
- 有多少种方式走到右下角
- 有多少种方法选出
k个数使得和是Sum:::- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求最大最小值
- 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出
k个数使得和是Sum
1.3 动态规划四大组成部分
1.3.1 确定状态
- 状态在动态规划中的作用属于定海神针
- 简单的说,解动态规划的时候需要开一个数组,数组的每个元素
f[i]或者f[i][j]代表什么?- 类似于解数学题中,X、Y、Z代表什么
确定状态需要两个意识
虽然我们不知道最优策略是什么,但是最优策略肯定是
K枚硬币面值加起来是27
- 所以一定有一枚
**最后的**硬币: - 除掉这枚硬币,前面硬币的面值加起来是
关键点1:我们不关心前面的
枚硬币是怎么拼出
的(可能有1种拼法,可能有100种拼法),而且我们现在甚至还不知道
和
,但是我们确定前面的硬币拼出了
关键点2:因为是最优策略,所以拼出
的硬币数一定要最少,否则这就不是最优策略了
子问题
- 所以我们就要求:最少用多少枚硬币可以拼出
- 原问题是最少用多少枚硬币拼出27
- 我们将原问题转化为一个子问题,而且规模更小:
- 为了简化定义,我们设状态
= 最少用多少枚硬币拼出
X - 等等,我们还不知道最后那枚硬币
是多少
- 最后那枚硬币
只可能是2、5或7
- 如果
,
f(27)应该是f(27-2) + 1(加上最后这一枚硬币2) - 如果
,
f(27)应该是f(27-5) + 1(加上最后这一枚硬币5) - 如果
,
f(27)应该是f(27-7) + 1(加上最后这一枚硬币7) - 除此以外,没有其他的可能了
1.3.2 转移方程
- 设状态
f[x]=最少用多少枚硬币拼出X - 对于任意
X
1.3.3 初始条件和边界情况
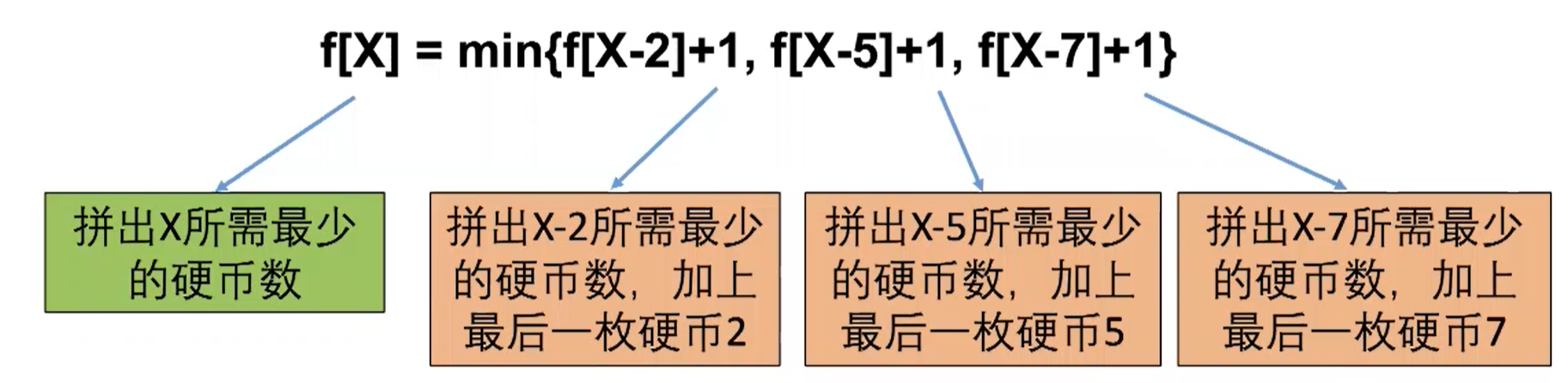
f[X] = min{f[X-2]+1,f[X-5]+1,f[X-7]+1}两个问题:X-2,X-5或者X-7小于0怎么办?什么时候停下来?- 如果不能拼出
Y,就定义f[Y]=正无穷- 例如f[-1] = f[-2] = . . . = 正无穷
- 所以
f[1] = min{f[-1]+1,f[-4]+1,f[-6]+1}=正无穷,表示拼不出来1 初始条件:
f[0] = 0**拼出X所需要的最少硬币数:f[X] = min{f[X-2]+1,f[X-5]+1,f[X-7]+1}**- 初始条件:
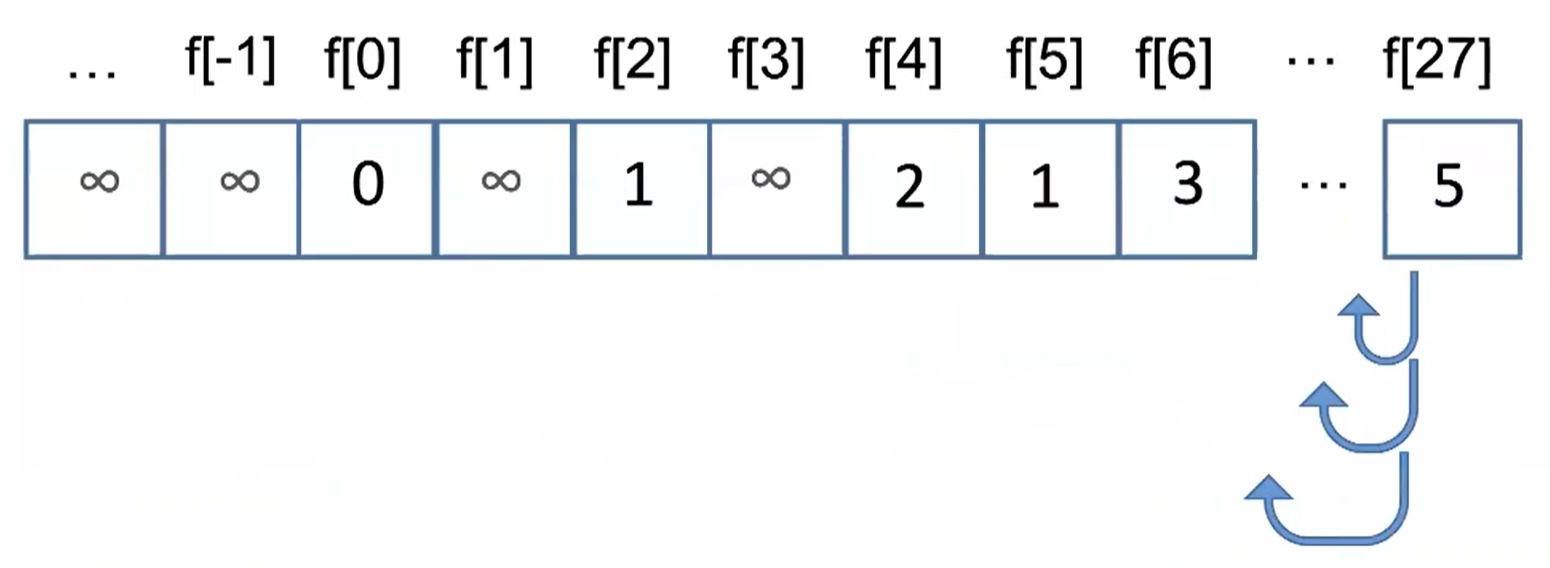
f[0] = 0 - 然后计算
f[1] f[2] ... f[27] - 当我们计算到
f[X]时,f[X-2] f[X-5] f[X-7]都已经得到结果了 f[X]= 最少用多少枚硬币拼出Xf[X]=表示无法用硬币拼出
X
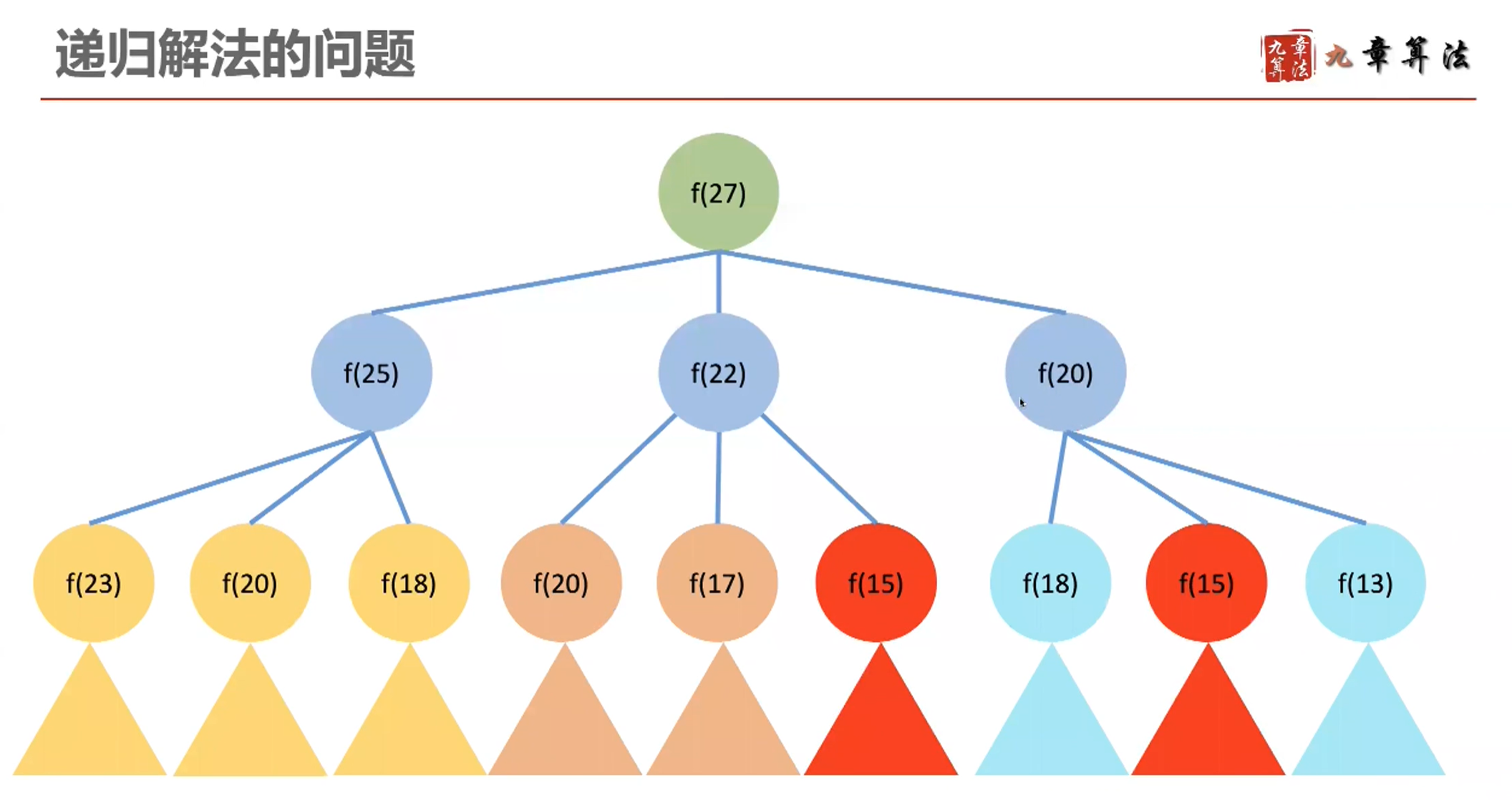
- 每一步尝试三种硬币,一共27步
- 与递归算法相比,没有任何重复计算
-
1.4 Onsite
:::tips
现场面试(报销食宿及飞机票)
- 时间:8:30~22:30
- 轮次:3~6轮 45m~1h
- 休息好!休息状态不好影响发挥
1.5 入门总结
四个组成部分
是否涵盖所有的动态规划考题类型
- 是
- 常见动态规划类型
- 坐标型动态规划(20%)
- 序列型动态规划(20%)
- 划分型动态规划(20%)
- 区间型动态规划(15%)
- 背包型动态规划(10%)
- 最长序列型动态规划(5%)
- 最长上升子序列
- 博弈型动态规划(5%)
- 综合型动态规划(5%)
- 区间博弈、序列划分
- DP + 二分、DP+Trie
- 动态规划时间空间优化
- FollowUp 常考:滚动数组、降维
- 动态规划打印路径
- 我需要什么基础才可以上这个班
- 学一门基础语言,写过20~30题,想对动态规划有透彻了解
- 这门课和九章算法班及算法强化班动态规划部分的关系
- 内容更加丰富、涵盖类型更广、题目更多更全
- 全面彻底解决面试中的老大难:动态规划问题
上完这门课我能学到什么
第一讲:动态规划入门
- 第二讲:坐标型动态规划
- 第三讲:序列型动态规划
- 第四讲:划分型动态规划
- 第五讲:区间和背包型动态规划
- 第六讲:双序列型动态规划
-
1.8 例题讲解
求值问题
-
1.9 暂时看不懂的
[x] 1.13 跳跃游戏
- 1.17 乘积最大子序列
1.10 题目解析
669 · 换硬币
解析
求最大最小值动态规划
:::tips
- 你有三种硬币,分别面值为2、5、7元,每种硬币都足够多
- 买一本书需要27元
- 如何用最少的硬币组合正好付清,不需要对方找钱
:::
直觉
:::tips
- 最少硬币组合—>尽量用面值大的硬币
- 7+7+7+5=26
:::
改变策略
:::tips
- 尽量用大的硬币,最后如果可以用一种硬币付清就行
- 7+7+7+2+2+2 = 27
- 6枚硬币,应该对了吧?
:::
正确答案:7+5+5+5+5 = 27,五枚硬币
题目
:::info 给出不同面额的硬币以及一个总金额. 写一个方法来计算给出的总金额可以换取的最少的硬币数量. 如果已有硬币的任意组合均无法与总金额面额相等, 那么返回 -1. :::
👋 你可以假设每种硬币均有无数个
总金额不会超过10000
硬币的种类数不会超过500, 每种硬币的面额不会超过100
样例
Input:
[1, 2, 5] 11
Output:
:::success
3
:::
Explain:
:::warning
11 = 5 + 5 + 1
:::
Input:
[2] 3
Output:
:::success
-1
:::
Explain:
:::warning
硬币数组中的值不满足和为amount = 3,故返回-1
:::
Input:
[1, 9] 0
Output:
:::success
0
:::
Explain:
:::warning
硬币数组中的值不满足和为amount = 3,故返回-1
:::
代码
import ("math")func CoinChange(coins []int, amount int) int {arr := make([]int, amount+1)n := len(coins)arr[0] = 0for i := 1; i <= amount; i++ {arr[i] = math.MaxInt//last coin//arr[i] = min{arr[i-coins[0]]+1, ... , f[i-coins[n-1]] + 1}for j := 0; j < n; j++ {//i 代表当前的钱数 当前钱数要 >= 硬币数组中的值if i >= coins[j] {arr[i] = min(arr[i-coins[j]]+1, arr[i])}}}if arr[amount] == 2<<31-1 {arr[amount] = -1}return arr[amount]}func min(x, y int) int {if x > y {return y}return x}
114 · 不同的路径
解析
计数型动态规划
:::tips
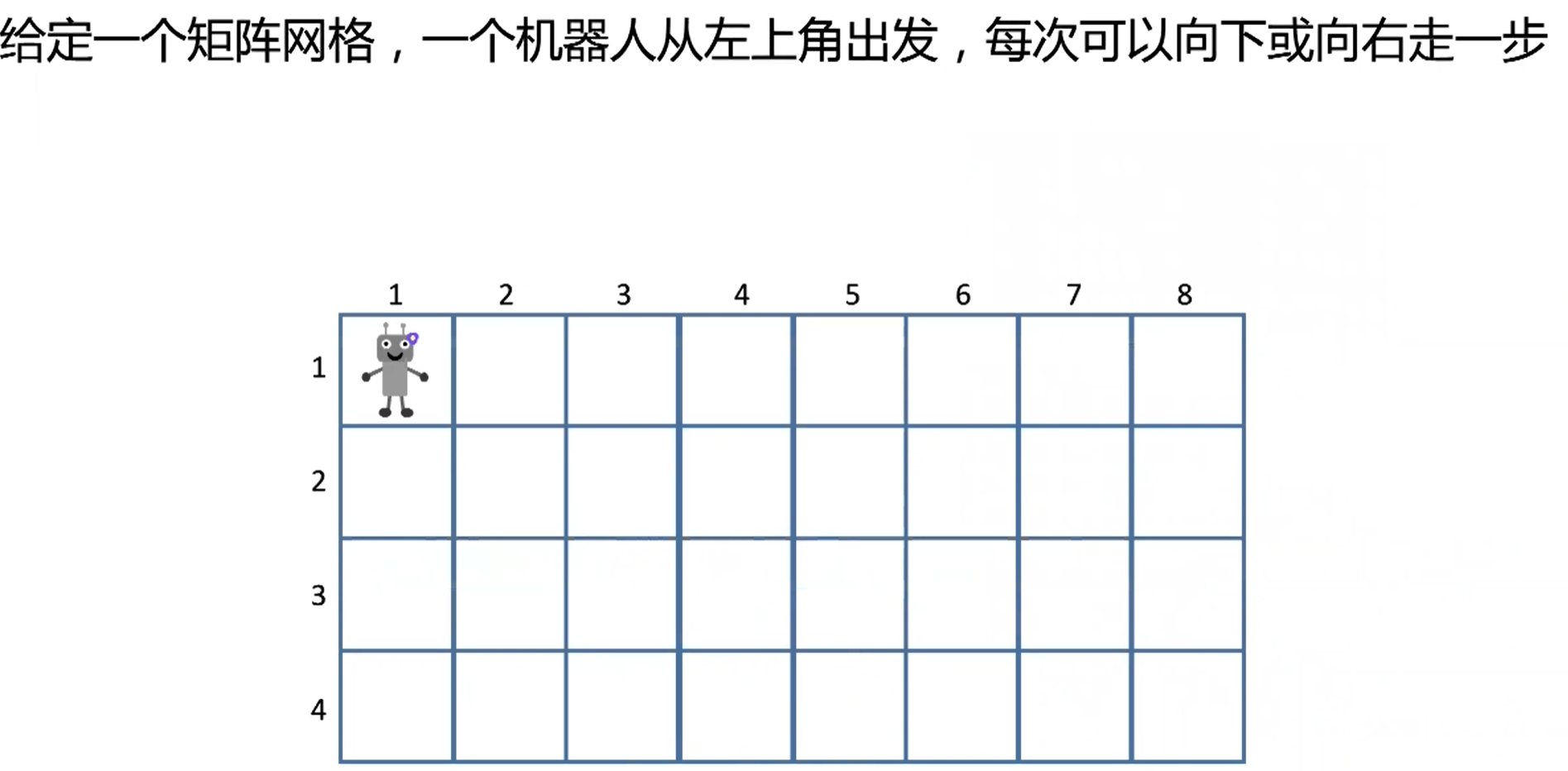
- 给定m行n列的网格,有一个机器人从左下角(0,0)出发,每一步可以向下或者向右走一步
- 问有多少种不同的方式走到右下角
:::
确定状态-最后一步:
- 无论机器人用何种方式到达右下角,总有最后挪动的一步:向右或向下
- 右下角坐标设为(m-1,n-1)
- 那么前一步机器人一定是在(m-2,n-1)或者(m-1,n-2)
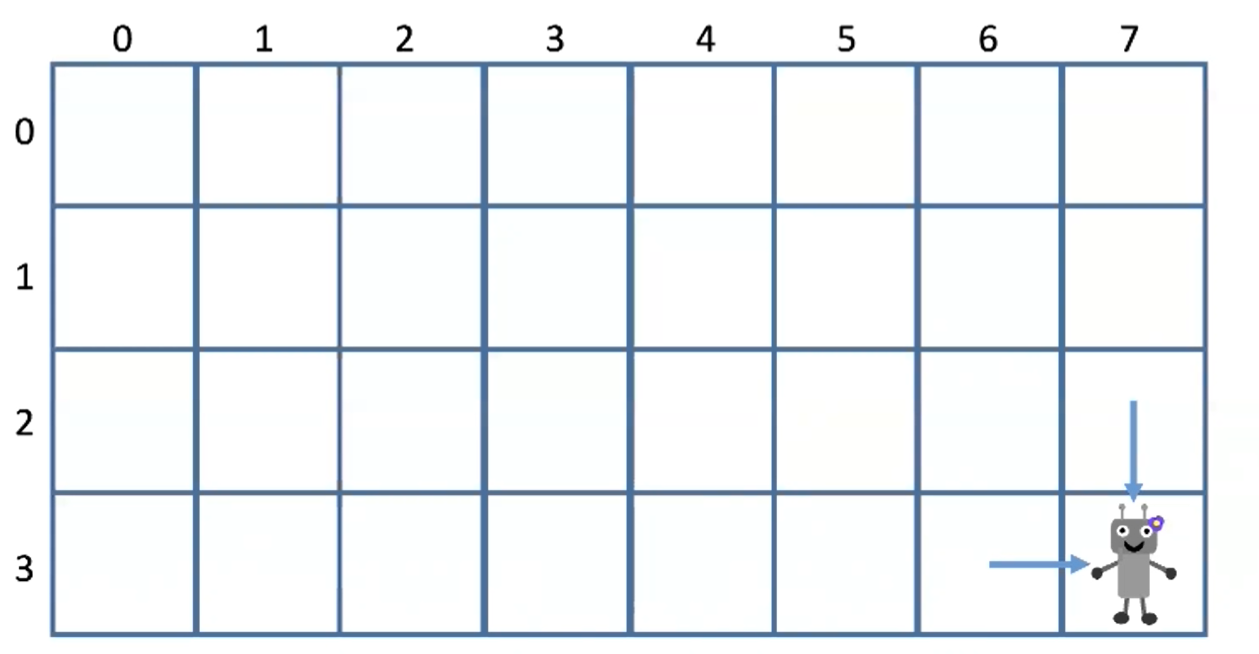
确定状态-子问题:
- 那么,如果机器人有
X种方式从左上角走到(m-2,n-1),有Y种方式从左上角走到(m-1,n-2),则机器人有X+Y种方式走到(m-1,n-1)- 问题转化为,机器人有多少种方式从左上角走到(m-2,n-1)和(m-1,n-2)
- 原题要求有多少种方式从左上角走到(m-1,n-1)
- 子问题
- 状态:设
f[i][j]为机器人有多少种方式从左上角走到(i,j)转移方程:
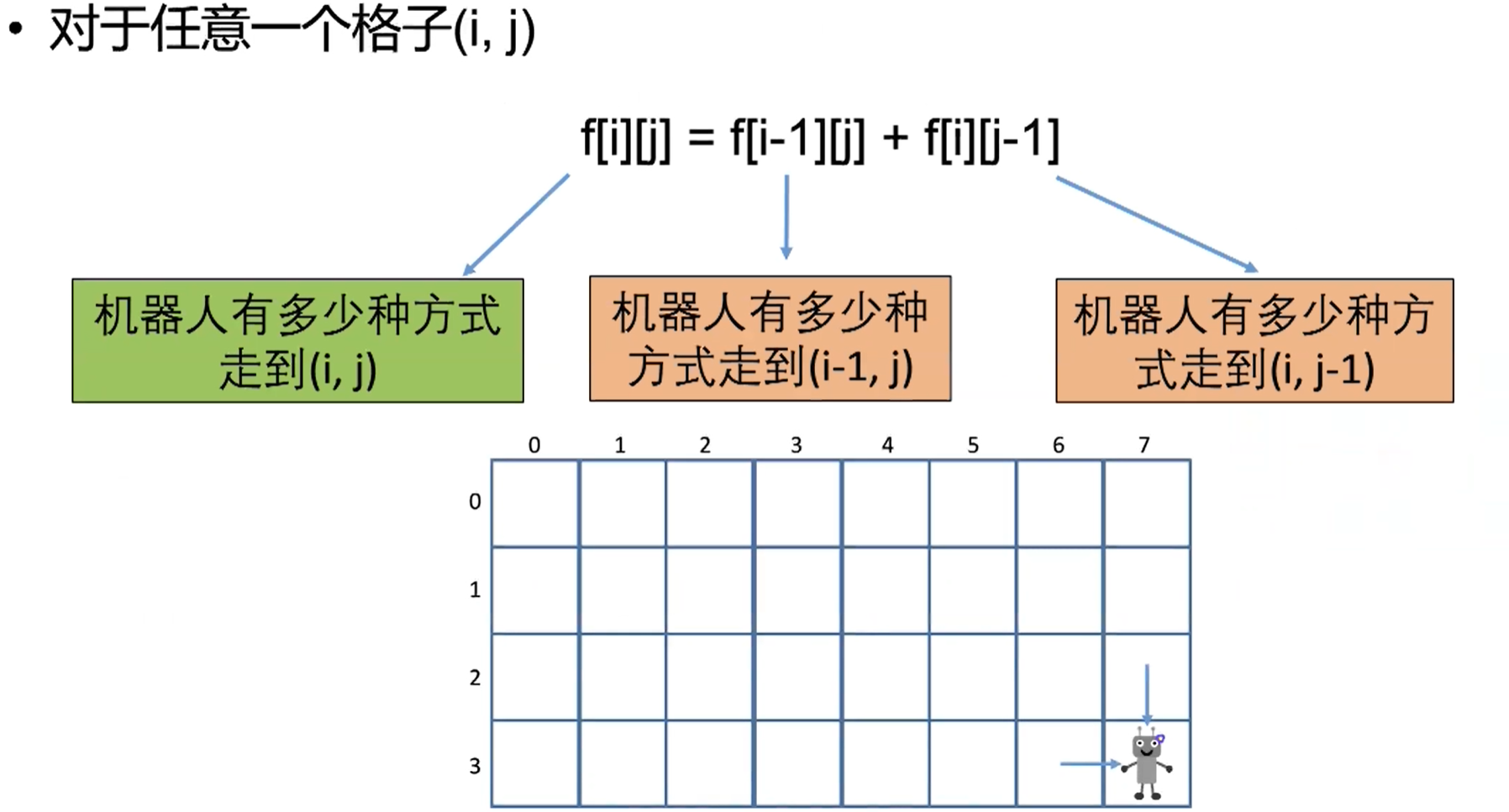
初始条件和边界情况:
- 初始条件:
f[0][0] = 1,因为机器人只有一种方式到左上角- 边界情况:
i = 0或j = 0,则前一步只能有一个方向过来—>f[i][j] = 1
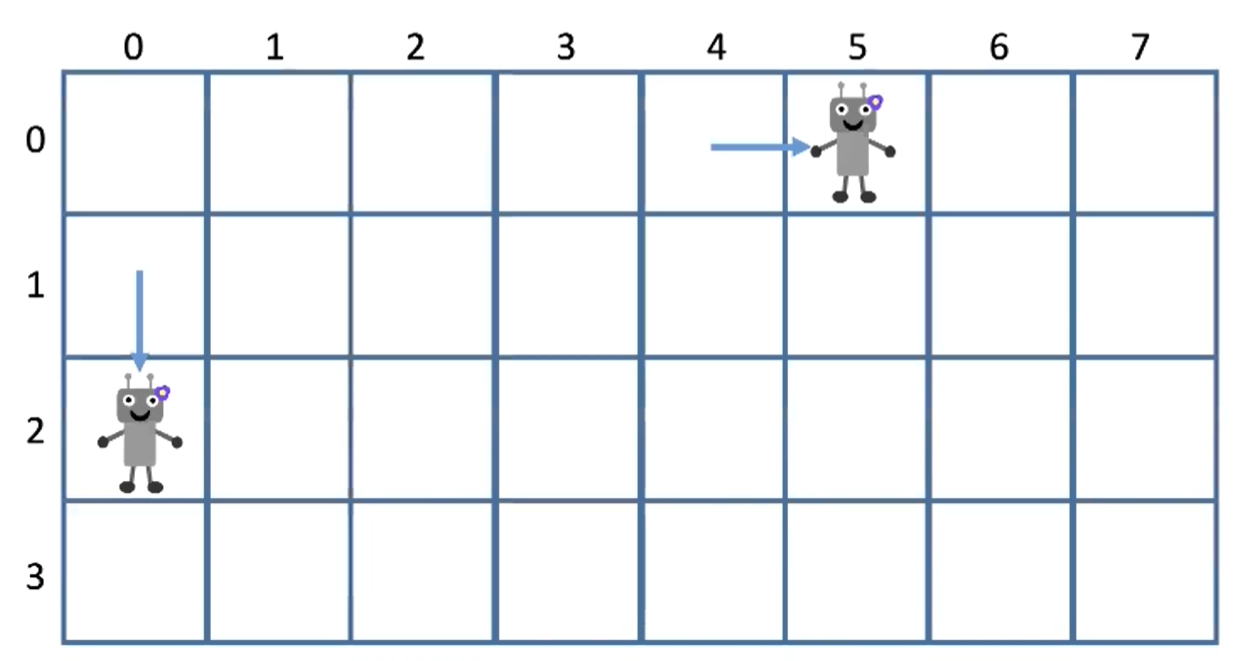
计算顺序:
f[0][0] = 1- 计算第
0行:f[0][0] f[0][1] ... f[0][n-1]- 计算第
1行:f[1][0] f[1][1] ... f[1][n-1]...- 计算第
m-1行:f[m-1][0] f[m-1][1] ... f[m-1][n-1]- 答案是
f[m-1][n-1]- 时间复杂度(计算步数):
O(MN),空间复杂度(数组大小):O(MN)
题目
:::info
有一个机器人的位于一个 m × n 个网格左上角。
机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。
问有多少条不同的路径?
:::
👋 n和m均不超过100
且答案保证在32位整数可表示范围内。
样例
Input:
n = 1 m = 3
Output:
:::success
1
:::
Explain:
:::warning
只有一条通往目标位置的路径。
:::
Input:
n = 3 m = 3
Output:
:::success
6
:::
Explain:
:::warning
D : Down
R : Right
func UniquePaths(m int, n int) int {// write your code heref := make([][]int, m)for i := 0; i < len(f); i++ {f[i] = make([]int, n)}for i := 0; i < len(f); i++ {for j := 0; j < len(f[0]); j++ {if i == 0 || j == 0 {f[i][j] = 1} else {f[i][j] = f[i-1][j] + f[i][j-1]}}}return f[m-1][n-1]}
116 · 跳跃游戏
解析
存在型动态规划
:::tips
- 有
n块石头分别在x轴的0 1 ... n-1位置 - 一只青蛙在石头
0,想跳到石头n-1 - 如果青蛙在第
i块石头上,它最多可以向右跳距离 - 问青蛙能否跳到石头
n-1:::确定状态:
- 最后一步:如果青蛙能跳到最后一块石头
n-1,我们考虑它跳的最后一步 - 这一步是从石头
i跳过来的,i<n-1 - 这需要两个条件同时满足:
- 青蛙可以跳到石头
i - 最后一步不超过跳跃的最大距离:
n-1-i<=
- 青蛙可以跳到石头
- 最后一步:如果青蛙能跳到最后一块石头

转移方程:
- 设
f[j]表示青蛙能不能跳到石头j

初始条件和边界情况:
- 设
f[j]表示青蛙能不能跳到石头jf[0] = True,因为青蛙一开始就在石头0计算顺序:
- 设
f[j]表示青蛙能不能跳到石头j- 初始化
f[0] = True- 计算
f[1] f[2] ... f[n-1]- 答案是
f[n-1]- 时间复杂度:
,空间复杂度(数组大小):
题目
:::info
给出一个非负整数数组,你最初定位在数组的第一个位置。
数组中的每个元素代表你在那个位置可以跳跃的最大长度。
判断你是否能到达数组的最后一个位置。
:::
👋 数组A的长度不超过5000,每个元素的大小不超过5000
样例
Input:
A = [2,3,1,1,4]
Output:
:::success
true
:::
Explain:
:::warning
0 -> 1 -> 4(这里的数字为下标)是一种合理的方案。
:::
Input:
A = [3,2,1,0,4]
Output:
:::success
false
:::
Explain:
:::warning
不存在任何方案能够到达终点
:::
代码
DP 动态规划
func CanJump(a []int) bool {// write your code heren := len(a)f := make([]bool, n)f[0] = truefor j := 1; j < n; j++ {f[j] = falsefor i := 0; i < j; i++ {if f[i] && i+a[i] >= j {f[j] = truebreak}}}return f[n-1]}
贪心
func CanJump(a []int) bool {far := 0n := len(a) - 1for i := 0; i < len(a); i++ {if far < i {return false}far = max(i+a[i], far)if far >= n {return true}}return false}func max(x, y int) int {if x > y {return x}return y}
191 · 乘积最大子序列
解析
:::tips
:::
:::tips
:::
:::tips
:::
题目
:::info
:::
👋
样例
Input:
Output:
:::success
:::
Explain:
:::warning
:::
Input:
Output:
:::success
:::
Explain:
:::warning
:::
Input:
Output:
:::success
:::
Explain:
:::warning