数据科学 Python
EDA：描述性统计——对样本的客观描述。
实质：由样本去推断总体的过程。
统计推断：参数估计和假设检验。
而统计推断离不开概率密度函数。

概率密度函数

表示连续随机变量X落在各值附近的可能性。
X一次抽样落入某区间的概率=概率密度函数在该区间上的积分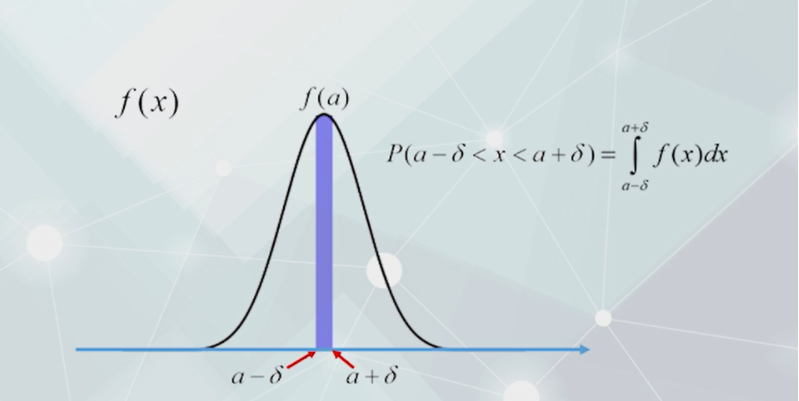
image.png
常见的概率密度函数有：

  • 正态分布
  • t-分布

  • 卡方分布

    正态分布

    正态分布函数是一个以均值为对称轴的钟形曲线，由均值和标准差两个独立参数控制。
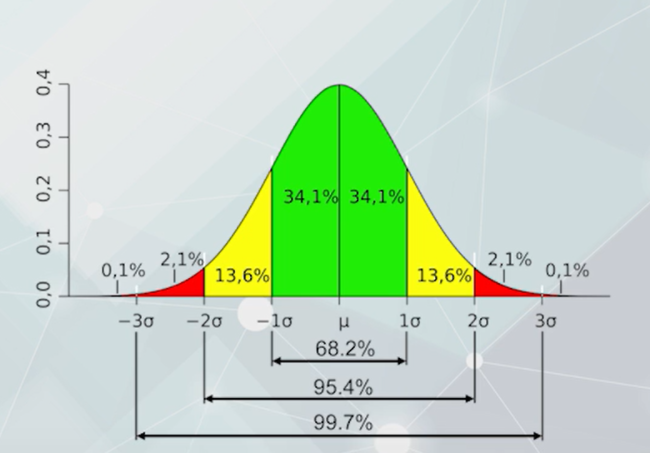
    image.png
    均值=0，标准差=1，标准正态分布服从高斯分布的随机变量：其落入均值加减两倍标准差范围内的概率是95.4%

    中心极限定理

    设X1，…，Xn是某一个均值，标准差为的总体的n个独立随机样本，则对于一个大的n(n>=30），无论总体分布是否为正态分布，都有近似 。

    卡方分布

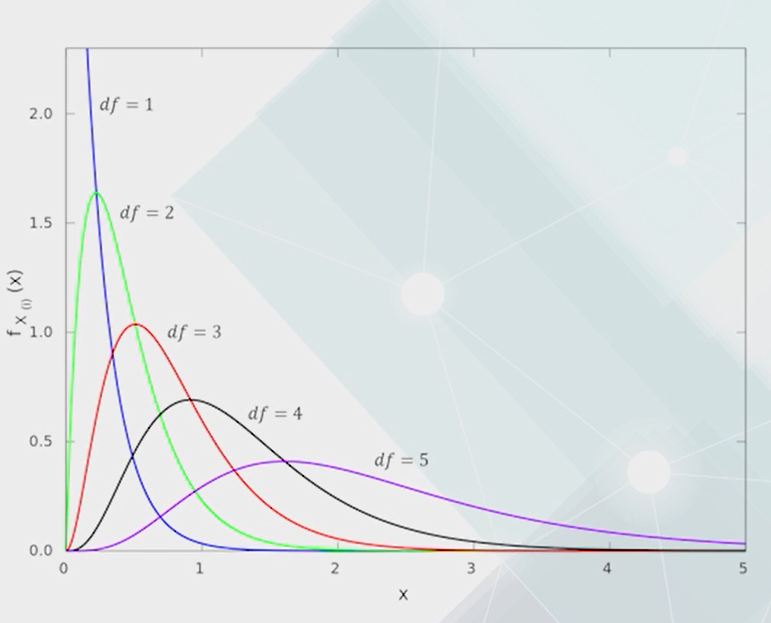
    image.png
    形状与自由度有关，n个服从标准正态分布的独立随机变量的平方和服从自由度为n的卡方分布。

    t-分布

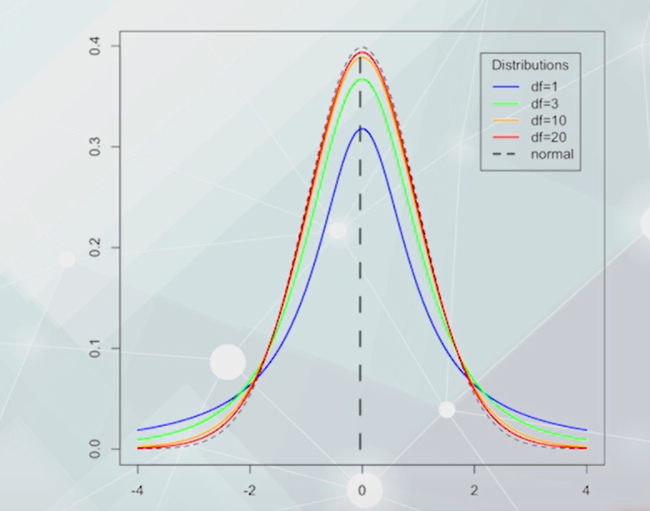
    image.png
    学生t分布：曲线形态也与自由度有关，而t分布的自由度是样本容量减1，与样本容量有关。
    N<30，自由度n-1的t-分布
    N≥30，高斯分布（中心极限定理)
    均值估计

    样本统计量(statistics）描述

    样本均值，样本标准差

    总体参数(parameters）描述

    均值，标准差
    基于样本的统计量而对总体分布的参数进行估计是参数估计。
    最基本的参数估计：均值和方差估计

    中心极限定理

  • 点估计：样本的统计就是总体均值的无偏估计。

  • 区间估计：在一个给定的置信水平alpha下，确定出置信区间，该区间会以alpha的概率包含总体均值。

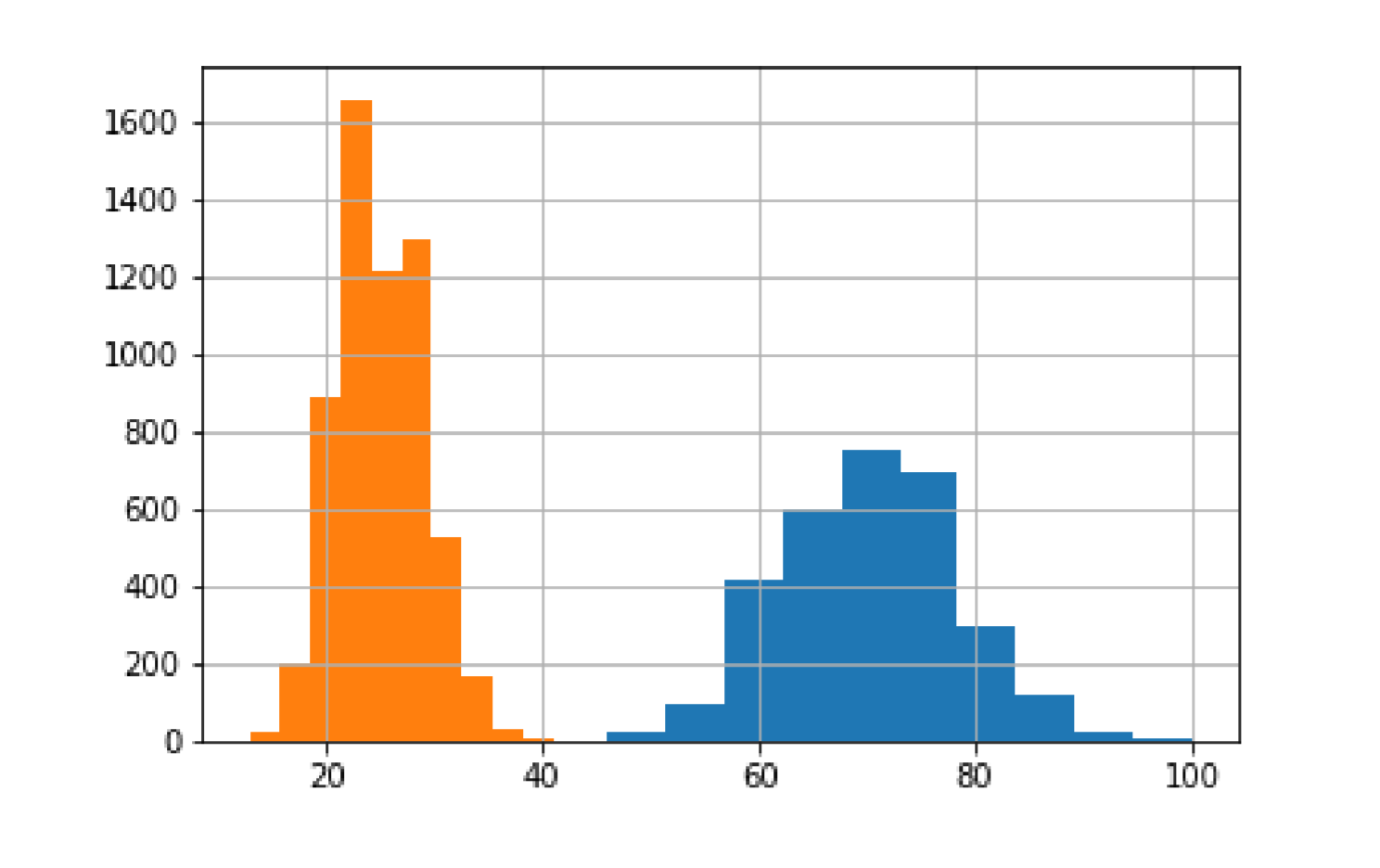
    1. import numpy as np
    2. import pandas as pd
    3. from scipy import stats
    4. np.random.seed(1234)
    5. my_data1=stats.poisson.rvs(loc=10,mu=60,size=3000) # 生成一个规定均值的泊松分布
    6. pd.Series(my_data1).hist().get_figure().show
    7. print('第一个分布的均值是：70,\t统计平均是：',my_data1.mean())
    8. my_data2=stats.poisson.rvs(loc=10,mu=15,size=6000)
    9. pd.Series(my_data2).hist().get_figure().show
    10. print('第二个分布的均值是：25，统计平均是：',my_data2.mean())
    11. my_data=np.concatenate((my_data1,my_data2)) # 一个典型的 bi-model 分布，以这 9000 个数作为总体
    12. print('总体的均值为: ',my_data.mean())
    13. sample_data=np.random.choice(a=my_data,size=100) # 从中随机抽取 100 个做样本
    14. print('样本的均值为: ',sample_data.mean())

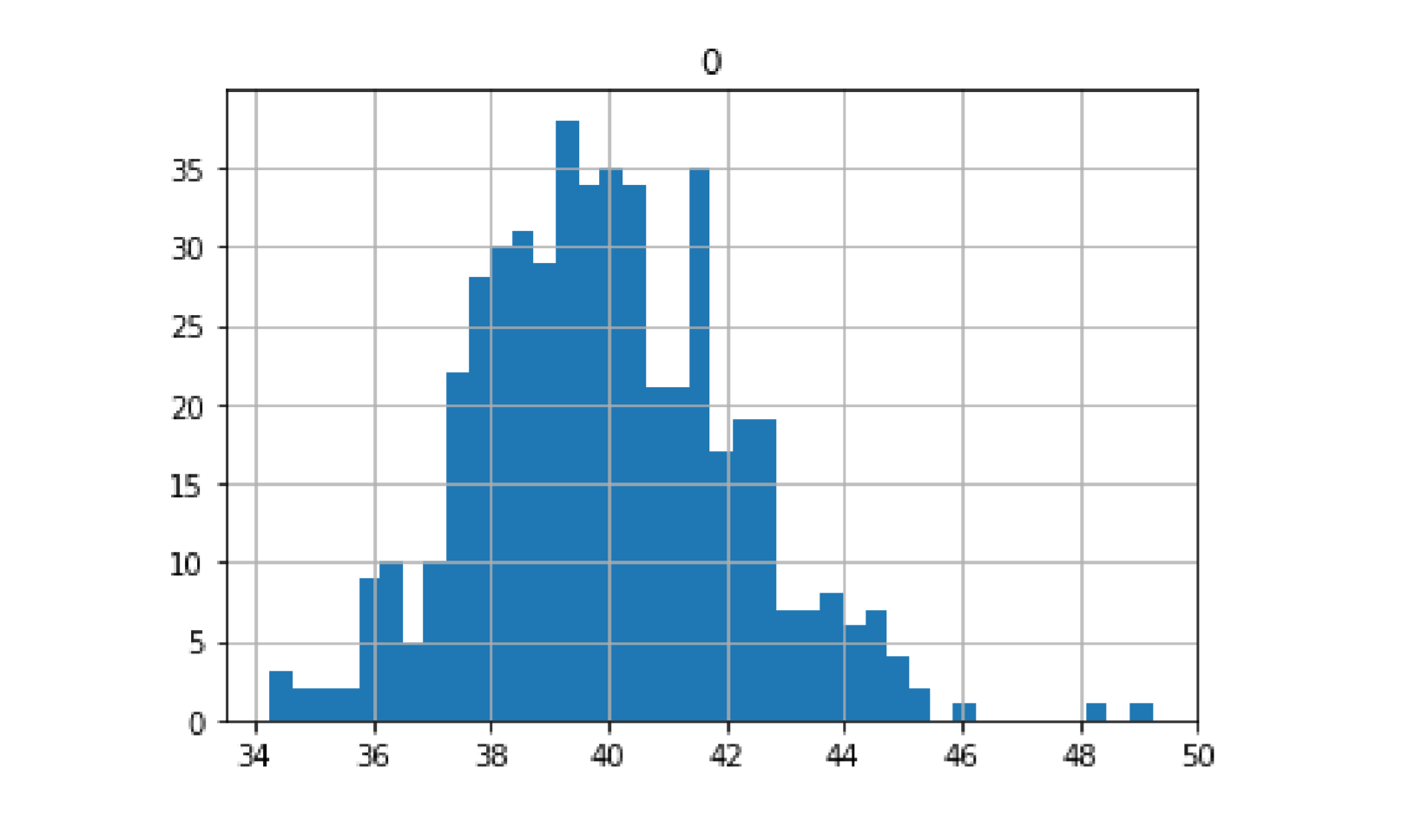
    image.png
    image.png

    1. point_estimates=[]
    2. for x in range(500): #500 次循环
    3.   sample=np.random.choice(a=my_data,size=100) # 每次随机抽样 100 个样本
    4.   point_estimates.append(sample.mean())
    5. pd.DataFrame(point_estimates).hist(bins=40) # 均值大致呈钟型分布
    6. print('样本均值的均值为: ', np.array(point_estimates).mean())

    image.png
    image.png

    1. sample_size=100
    2. sample=np.random.choice(a=my_data,size=sample_size)
    3. sigma=sample.std()/(sample_size)**0.5
    4. stats.t.interval(alpha=0.95, # 置信水平 confidence level
    5.                df=sample_size-1, # 自由度 Degrees of freedom
    6.                loc=sample.mean(),
    7.                scale=sigma)
    8. # 返回拥有 95% 置信水平的置信区间

    image.png

    方差估计

    设X1,…，Xn是某一个均值，标准差为的总体的随机样本，在样本量为n的所有随机样本中，样本方差S2是的无偏估计
    即
    其中

    不同的数据分组之间做比较

    比较测试组和对照组到底有没有差异
    A/B Testing中控制因素到底对观察变量有没有影响

    假设检验

    第一步：提出假设
    第二步：验证是否可以接受假设
    零假设(null hypothesis): H0，需要检验的假设。

  • 总体的均值等于;

  • 测试组和对照组来源于均值相等的总体;
  • 控制因素对观察变量没有影响，A组和B组数据同分布;

替代假设(alternative hypothesis): H1（或Ha），某种意义上与H0相反的假设。

  • 总体的均值不等于;
  • 测试组和对照组来源于均值不相等的总体;
  • 控制因素对观察变量有影响，A组和B组数据不同分布; | | | 真实性 | | | —- | —- | —- | —- | |
    | | H0 | H1 | | 判定 | 接受H0 | | II型错误 | | | 拒绝H0 | I型错误 | |

单样本均值检验

  1. import numpy as np
  2. import pandas as pd
  3. from scipy import stats
  4. import matplotlib.pyplot as plt
  5. from scipy.stats import t
  6. np.random.seed(1234)
  7. my_data1=stats.poisson.rvs(loc=10,mu=60,size=3000) # 生成一个规定均值的泊松分布
  8. #pd.Series(my_data1).hist().get_figure().show
  9. #print(' 第一个分布的均值是：70,\t 统计平均是：',my_data1.mean())
  10. my_data2=stats.poisson.rvs(loc=10,mu=15,size=6000)
  11. #pd.Series(my_data2).hist().get_figure().show
  12. #print(' 第二个分布的均值是：25，统计平均是：',my_data2.mean())
  13. my_data=np.concatenate((my_data1,my_data2))
  14. # 一个典型的 bi-model 分布，我们以这 9000 个数作为总体
  15. #print(' 总体的均值为: ',my_data.mean()) # 假装我们不知道
  16. # 现在根据样本，验证 H0: 总体的均值是 47.5
  17. # 这是单样本双边 t 检验，one-sample t-test
  18. print('空假设 H0 是：总体的均值是 47.5 \n')
  19. sample_data=np.random.choice(a=my_data,size=100) # 从中随机抽取 100 个做样本
  20. t_statistic,p_value=stats.ttest_1samp(a=sample_data,popmean=47.5)
  21. print('从样本构造的 t 统计量 = ',t_statistic)
  22. #t 的绝对值越大，p 值越小，可参见下面的 t-分布图
  23. print('单样本双边检验的 p = ',p_value)
  24. # 画一下样本容量为 100 时的 t 分布曲线
  25. df=100-1
  26. x = np.linspace(stats.t.ppf(0.00000001,df),stats.t.ppf(0.99999999,df),100)
  27. #ppf 函数是 CDF 的逆函数，用来求分位点
  28. plt.plot(x, t.pdf(x, df)) #pdf 生成概率密度函数表
  29. plt.plot((t_statistic,t_statistic),(-0.01,0.4),'-.r')
  30. str_legend=('t distribution','calculated t')
  31. plt.legend(str_legend)
  32. plt.show()

image.png

  1. x = np.linspace(stats.t.ppf(0.00000001,df),stats.t.ppf(0.99999999,df),100)
  2. #ppf 函数是 CDF 的逆函数，用来求分位点
  3. plt.plot(x, t.pdf(x, df)) #pdf 生成概率密度函数表
  4. plt.plot((t_statistic,t_statistic),(-0.01,0.4),'-.r')
  5. str_legend=('t distribution','calculated t')
  6. plt.legend(str_legend)
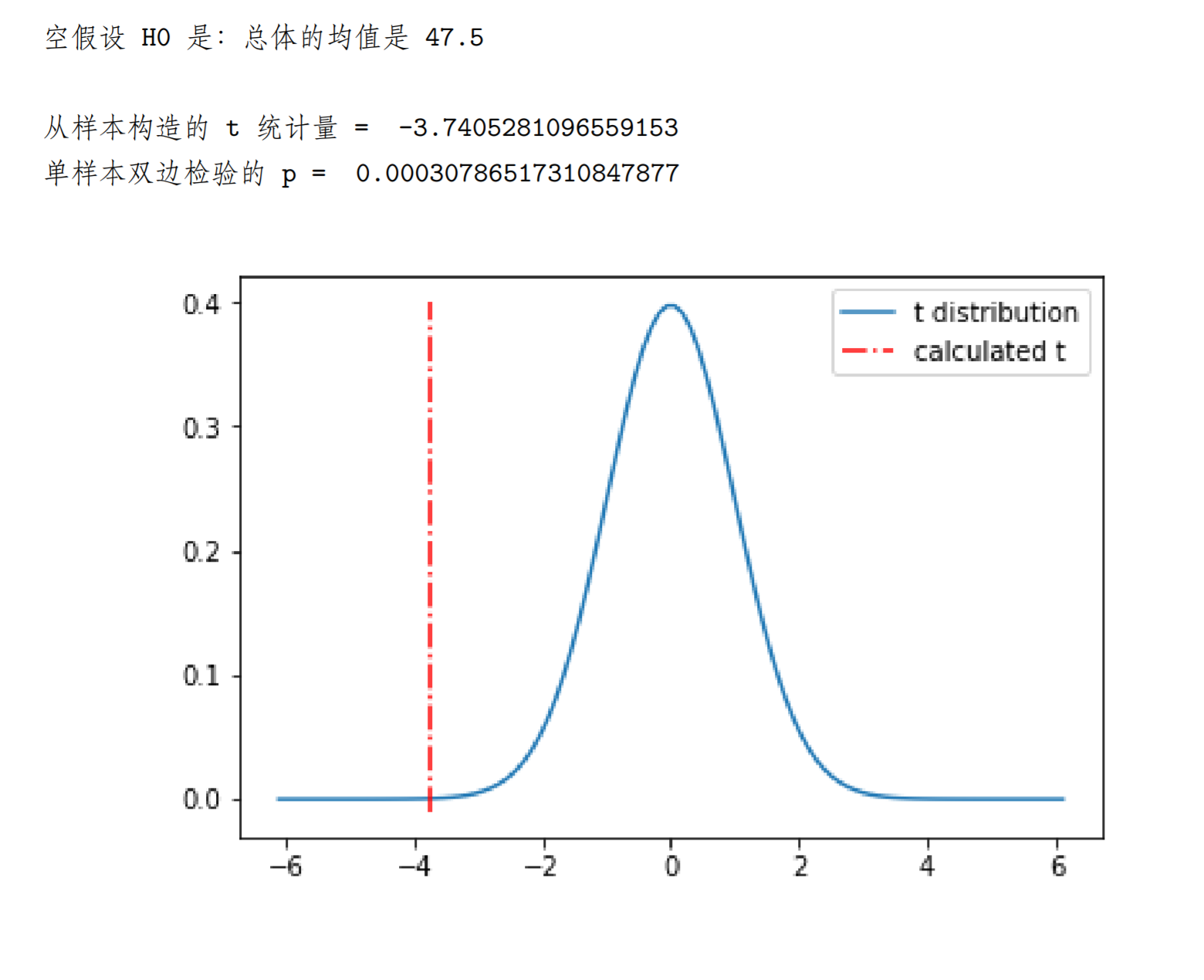
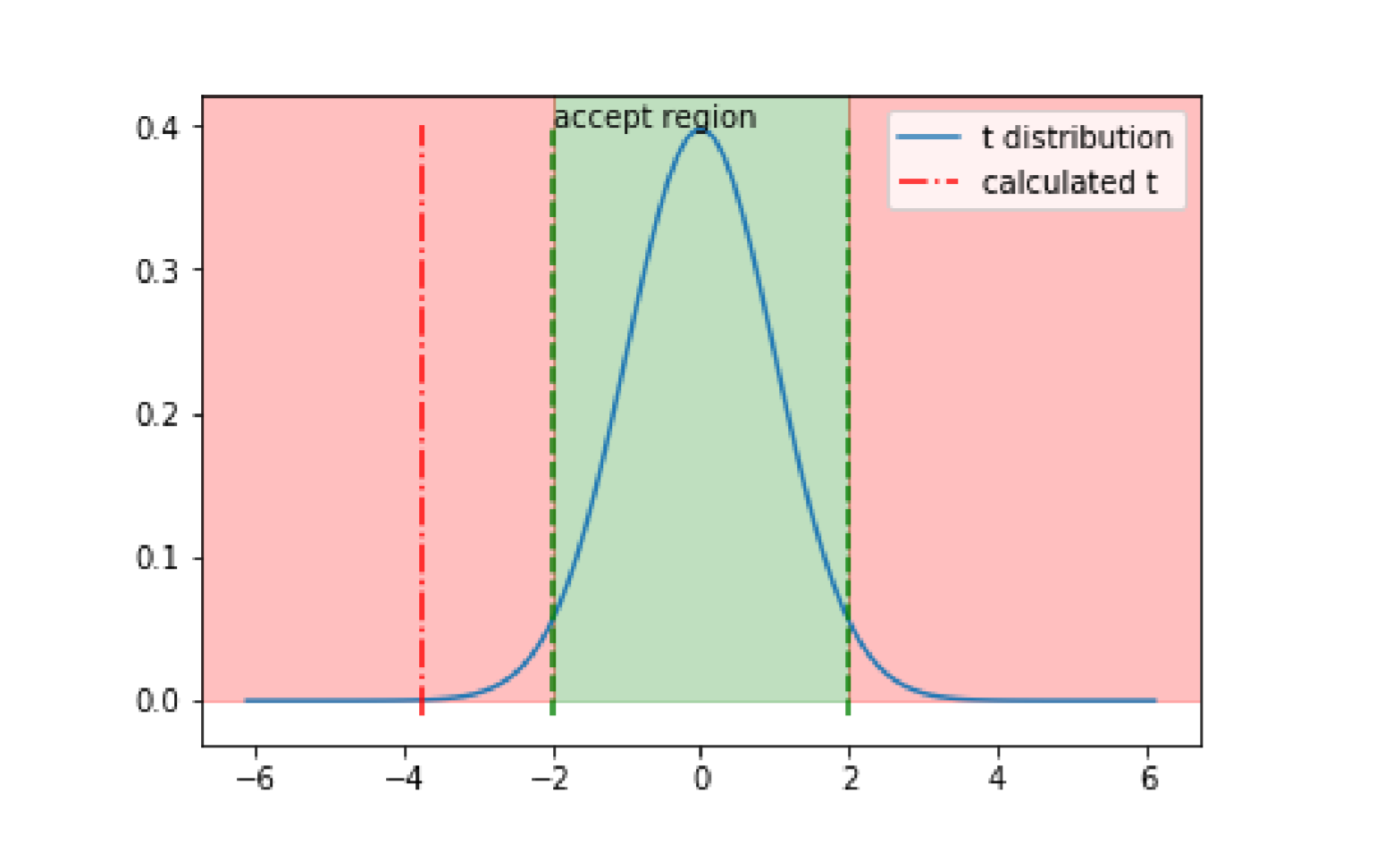
  7. x_025=stats.t.ppf(0.025,df)
  8. # 注意：同样选取 alpha=0.5，做双边 test 时要给左、右两侧各分配 0.25
  9. plt.plot((x_025,x_025),(-0.01,0.4),'--g') # 这根线是双边检验的左阈值
  10. x_975=stats.t.ppf(0.975,df)
  11. plt.plot((x_975,x_975),(-0.01,0.4),'--g') # 这根线是双边检验的右阈值
  12. #print(x_975)
  13. rect1=plt.Rectangle((x_025,0),x_975*2,0.5,color='g',alpha=0.25)
  14. plt.gca().add_patch(rect1)
  15. rect2=plt.Rectangle((x_975,0),5,0.5,color='r',alpha=0.25)
  16. plt.gca().add_patch(rect2)
  17. rect3=plt.Rectangle((x_025,0),-5,0.5,color='r',alpha=0.25)
  18. plt.gca().add_patch(rect3)
  19. #plt.ylim(-0.02,0.5)
  20. plt.text(x_025,0.4,'accept region') # 图片上不支持中文
  21. #plt.savefig('111.png') # 不支持中文文件名
  22. plt.show()

image.png

  1. print('p = ',p_value,'\n')
  2. alpha=0.05
  3. if p_value>=0.05:
  4.     print('\033[1;31m 接受 \033[0m H0')
  5. else:
  6.     print('\033[1;31m 拒绝
  7.     \033[0m H0, 即总体的均值不等于 47.5，此时错误拒绝 H0 的概率为
  8.     ',p_value,'小于显著性水平')

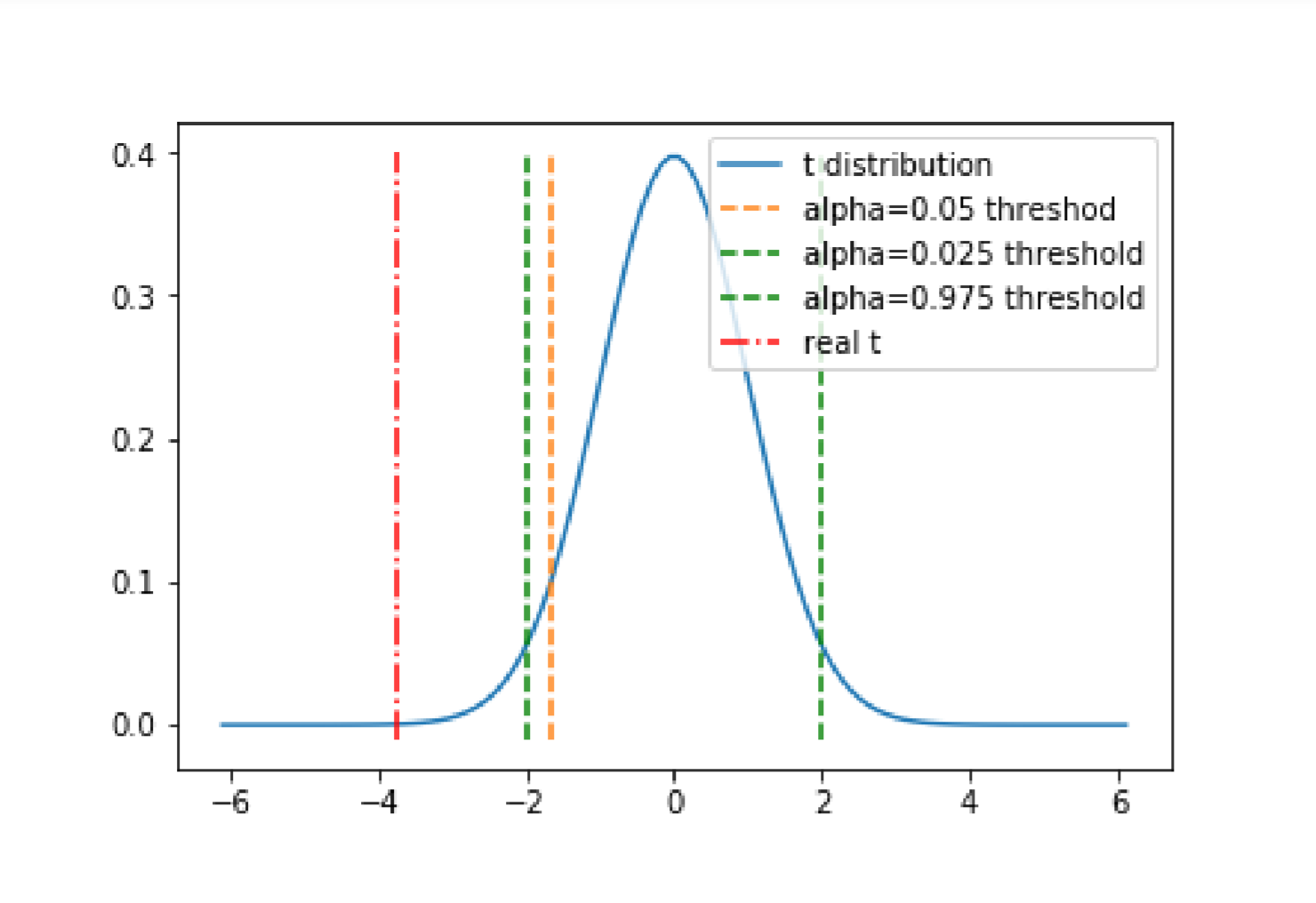
image.png

  1. import numpy as np
  2. import pandas as pd
  3. from scipy import stats
  4. from scipy.stats import t
  5. import matplotlib.pyplot as plt
  7. str_legend=('t distribution','alpha=0.05 threshod','alpha=0.025 threshold',\
  8. 'alpha=0.975 threshold','real t')
  9. # 画一下样本容量为 100 时的 t 分布曲线
  10. df=100-1
  11. #a=0.05 # 自定义的显著性水平
  12. x = np.linspace(stats.t.ppf(0.00000001,df),stats.t.ppf(0.99999999,df),100)
  13. #ppf 函数是 CDF 的逆函数，用来求分位点
  14. plt.plot(x, t.pdf(x, df), alpha=1)
  15. # 注意此 alpha 是 plot 方法中的透明度参数，不是显著性参数
  16. x_05=stats.t.ppf(0.05,df) #p(t<x_05)=0.05
  17. #print(x_05)
  18. plt.plot((x_05,x_05),(-0.01,0.4),'--') # 这根线是单边检验的阈值
  19. x_025=stats.t.ppf(0.025,df)
  20. # 注意：同样选取 alpha=0.5，做双边 test 时要给左、右两侧各分配 0.25
  21. plt.plot((x_025,x_025),(-0.01,0.4),'--g') # 这根线是双边检验的左阈值
  22. x_975=stats.t.ppf(0.975,df)
  23. plt.plot((x_975,x_975),(-0.01,0.4),'--g') # 这根线是双边检验的右阈值
  24. t_real=stats.t.ppf(p_value/2,df)
  25. # 上一个 cell 中我们做的是双边 t-test，因此这里找分位点时，p 值要除以 2
  26. print('从样本获得的 t 统计量是',t_real)
  27. plt.plot((x_real,x_real),(-0.01,0.4),'-.r')
  28. # 各阈值截断的曲线下面积对应 I 型错误率
  29. plt.legend(str_legend)
  30. plt.show()

image.png
image.png

I型错误率达到多少时拒绝空假设?

设置显著性水平：alpha
当p确保I型错误率≤alpha

双样本均值检验

  • t-检验
  • 构造统计量
    1. np.random.seed(1234)
    2. my_data1=stats.poisson.rvs(loc=10,mu=60,size=3000) # 生成一个规定均值的泊松分布
    3. #pd.Series(my_data1).hist().get_figure().show
    4. #print(' 第一个分布的均值是：70,\t 统计平均是：',my_data1.mean())
    5. my_data2=stats.poisson.rvs(loc=10,mu=15,size=6000)
    6. #pd.Series(my_data2).hist().get_figure().show
    7. #print(' 第二个分布的均值是：25，统计平均是：',my_data2.mean())
    8. my_data=np.concatenate((my_data1,my_data2))
    9. # 一个典型的 bi-model 分布，我们以这 9000 个数作为总体
    10. my_sample={}
    11. for n in range(2):
    12.   my_sample[n]=np.random.choice(a=my_data,size=100) # 从中随机抽取 100 个做样本
    13.   print('第',n,'组样本的均值为',my_sample[n].mean())
    14. print('根据样本均值，能否下结论说两组样本来源的总体其均值不相等呢？')
    15. # 需进行 two sample t-test
    16. #H0: 两样本均值相等
    image.png
    两组的统计方差、样本容量均相等可以使用ttest-ind函数
    1. # 能否下结论说两组样本来源的总体其均值不相等呢？
    2. # 需进行 two sample t-test
    3. #H0: 两样本均值相等
    4. alpha=0.01 # 设置显著性水平
    5. t_statistic,p_value=stats.ttest_rel(a=my_sample[0],b=my_sample[1])
    6. #sample size 相等的双样本均值比较
    7. print('t = ',t_statistic)
    8. print('p = ',p_value)
    9. if p_value<=alpha:
    10.   print('\033[1;31m 拒绝 \033[0m H0：两样本来源的总体均值相等 ')
    11. else:
    12.   print('\033[1;31m 接受 \033[0m the H0: 两样本来源的总体均值相等')
    image.png

    卡方检验应用

    卡方检验：检验类别数据在各类上的分布是否与给定的概率分布一致。
    【例】Titanic船难中，幸存者中是否真的是女性居多。
    全球性别分布VS登船人员中的性别分布
    研究对象——幸存者中的性别分布
    H0：幸存者中的性别分布与船上所有人的性别分布一致
    替代假设则是不一致。
    1. #Titanic 数据存活人的类别分析
    2. # 探究性别与存活是否为关联事件
    3. # 如果性别与存活与否无关，则存活人群中的性别比应与全体人的一致，全体是什么？
    4. # 是船上所有人，还是所有人（即 0.5:0.5）
    5. import pandas as pd
    6. import numpy as np
    7. from scipy import stats
    8. from scipy.stats import chi2
    9. from matplotlib import pyplot as plt
    10. titanic = pd.read_csv("C:\Python\Scripts\my_data\Titanic.csv")
    11. # 对全体做性别统计
    12. mask1=titanic['Sex']=='male'
    13. mask2=titanic['Sex']=='female'
    14. p=np.array([sum(mask1)/(sum(mask1)+sum(mask2)),sum(mask2)/(sum(mask1)+sum(mask2))])
    15. print(p)
    16. mask_survived=titanic['Survived']==0
    17. # 如果反过来做，活着的人中，性别比满足 p 吗？请同学们验证
    18. my_population=titanic.loc[mask_survived,'Sex']
    19. print(type(my_population))
    20. pop_size=my_population.count()
    21. print('总体大小是 ',pop_size)
    22. sample=my_population
    23. E=pop_size*p
    24. print( '预期的男、女个数是 ',E)
    25. mask1=sample=='male'
    26. mask2=sample=='female'
    27. my_set1=sample[mask1]
    28. my_set2=sample[mask2]
    29. O=np.array([len(my_set1),len(my_set2)])
    30. print('实际的男女个数是 ',O)
    31. chi_squard,p_value=stats.chisquare(f_obs=O,f_exp=E)
    32. print(chi_squard,p_value)
    33. a=0.05
    34. df=1 # 只有两个类别，因此自由度是 2-1=1
    35. if p_value<=a:
    36.   print('我们 \033[1;31m 拒绝 \033[0m 男性女性具有相同死亡率的假设.')
    37. else:
    38.   print('我们 \033[1;31m 接受 \033[0m 男性女性具有相同死亡率的假设')
    image.png

    统计检验

  1. 提出空假设和替代假设
  2. 选择显著性水平，进行合适的检验
  3. 将p值与显著性水平比较
  4. 接受或拒绝空假设

p值：基于当前样本和空假设，现有统计量落入当前值及以外区域的概率。
显著性水平alpha：拒绝接受空假设的门限。
p值 > alpha，接受域
p值本质：p与alpha都反映的是I型错误率。