时间序列

MidiMax压缩算法

简介

在很多时间序列问题中，例如金融时序数据，经常需要对其进行可视化以方便了解数据，都知道金融数据是非常巨大的，所以如果需要可视化的话需要花费较多的RAM，磁盘等计算存储资源，介绍一种压缩算法“Midimax”，该算法会通过数据大小压缩来提升时间序列图的效果。该算法的设计有如下几点目标：

  1. 不引入非实际数据。只返回原始数据的子集，所以没有平均、中值插值、回归和统计聚合等；
  2. 快速且计算量小；
  3. 它应该最大化信息增益。这意味着它应该尽可能多地捕捉原始数据中的变化；

  4. 由于取最小和最大点可能会给出夸大方差的错误观点，因此取中值点以保留有关信号稳定性的信息。

    Midimax压缩算法

    算法伪代码

  5. 向算法输入时间序列数据和压缩系数（浮点数）。

  6. 将时间序列数据拆分为大小相等的非重叠窗口，其中大小计算为：3表示从每个窗口获取的最小、中值和最大点。因此，要实现2的压缩因子，窗口大小必须为6。更大的压缩比需要更宽的窗口。
  7. 按升序对每个窗口中的值进行排序。
  8. 选取最小点和最大点的第一个和最后一个值。这将确保最大限度地利用差异并保留信息。
  9. 为中间值选取一个中间值，其中中间位置定义为。因此，即使窗口大小是均匀的，也不会进行插值。
  10. 根据原始索引（即时间戳）对选取的点重新排序。

    案例展示

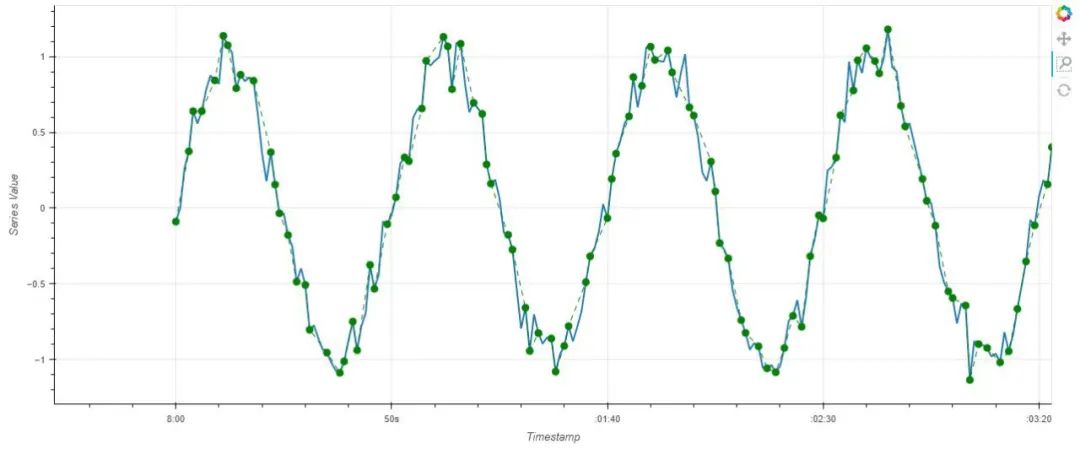
    可视化大型时间序列的技巧 - 图1
  • 蓝色是原始的图；

  • 绿色的点是Midimax算法给出的图。

    代码

    1. '''
    2. 代码摘自：https://medium.com/towards-data-science/midimax-data-compression-for-large-time-series-data-daf744c89310
    3. '''
    4. import pandas as pd
    5. def compress_series(inputser: pd.Series, compfactor=2):
    6.   """
    7.   Split into segments and pick 3 points from each segment, the minimum,
    8.   median, and maximum. Segment length = int(compfactor x 3). So, to achieve a
    9.   compression factor of 2, a segment length of 6 is needed.
    10.   Parameters
    11.   ----------
    12.   inputser : pd.Series
    13.       Input data to be compressed.
    14.   compfactor : float
    15.       Compression factor. The default is 2.
    16.   Returns
    17.   -------
    18.   pd.Series
    19.       Compressed output series.
    20.   """
    21.   # If comp factor is too low, return original data
    22.   if (compfactor < 1.4):
    23.       return inputser
    25.   win_size = int(3 * compfactor)  # window size
    27.   # Create a column ofsegment numbers
    28.   ser = inputser.rename('value')
    29.   ser = ser.round(3)
    30.   wdf = ser.to_frame()
    31.   del ser
    32.   start_idxs = wdf.index[range(0, len(wdf), win_size)]
    33.   wdf['win_start'] = 0
    34.   wdf.loc[start_idxs, 'win_start'] = 1
    35.   wdf['win_num'] = wdf['win_start'].cumsum()
    36.   wdf.drop(columns='win_start', inplace=True)
    37.   del win_size, start_idxs
    39.   # For each window, get the indices of min, median, and max
    40.   def get_midimax_idxs(gdf):
    41.       if len(gdf) == 1:
    42.           return [gdf.index[0]]
    43.       elif gdf['value'].iloc[0] == gdf['value'].iloc[-1]:
    44.           return [gdf.index[0]]
    45.       elif len(gdf) == 2:
    46.           return [gdf.index[0], gdf.index[1]]
    47.       else:
    48.           return [gdf.index[0], gdf.index[len(gdf) // 2], gdf.index[-1]]
    50.   wdf = wdf.dropna()
    51.   wdf_sorted = wdf.sort_values(['win_num', 'value'])
    52.   midimax_idxs = wdf_sorted.groupby('win_num').apply(get_midimax_idxs)
    54.   # Convert into a list
    55.   midimax_idxs = [idx for sublist in midimax_idxs for idx in sublist]
    56.   midimax_idxs.sort()
    57.   return inputser.loc[midimax_idxs]

    小结

    Midimax是一种简单轻量级的算法，可以减少数据的大小，并进行快速的图形绘制，可以发现：

  • Midimax在绘制大型时序图时可以保留原始时序的趋势；可以使用较少的点捕获原始数据中的变化，并在几秒钟内处理大量数据。

  • Midimax会丢失部分细节；压缩过大的话可能会有较多信息丢失。

    参考文献

    https://github.com/edwinsutrisno/midimax_compression